不确定超声速导弹简化模型的滑模控制研究
晋玉强,李泽雪,雷军委
(海军航空工程学院,山东 烟台 264001)
不确定超声速导弹简化模型的滑模控制研究
晋玉强,李泽雪,雷军委
(海军航空工程学院,山东 烟台 264001)
针对于超声速导弹的参数时变、不确定的特点,在超声速导弹简化模型的基础上研究了滑模变结构控制方法,通过理论分析和仿真实践证明了滑模控制系统对于不确定系统具有较好的控制效果。并且与PID控制方法进行了对比,发现了滑模控制方法较PID控制方法具有更强的鲁棒性。证明了滑模法对于不确定超声速导弹的有效性。
滑模控制;不确定超声速导弹;PID控制
0 引言
导弹的气动参数会随其飞行速度、飞行高度和大气密度而变化,特别是导弹的飞行速度和飞行高度的变化范围很大,因而导弹的数学模型参数也可以在很大的范围内变化。在飞行过程中,导弹的质量和质心位置会随着燃料的消耗而改变,这也会影响其数学模型的参数。当对象的数学模型参数在小范围内变化时,可用一般的反馈控制、最优控制或补偿控制等方法来消除或减小参数变化对控制品质的有害影响。超声速导弹的飞行速度非常快,在导弹的飞行时间内,控制对象的参数变化范围大,所以上面这些方法就不能圆满解决问题了[1-5]。
滑模变结构控制(Sliding Mode Control,SMC)以其独特的优点,如算法简单,不要求被控对象具有精确的数学模型,当系统参数摄动和外界干扰符合完全匹配条件时,控制系统对它们具有不变性等[6-10],所以非常适合导弹控制系统设计。考虑到滑模变结构控制的优点,本文决定采用该方法来设计超声速导弹控制系统。
本文在超声速导弹简化二阶模型的基础上,对滑模控制系统进行了研究,提出了二阶滑模控制算法的一般概念和典型的滑模到达条件[11-12],根据该到达条件可以得到系统的控制器,最后将算法用于导弹控制系统设计,获得了一些有实用价值的结论和方法。论文研究成果为滑模控制算法的研究注入了新思想,同时也为导弹控制系统设计提供了一种新的解决方案。因此,本课题的研究不仅具有理论意义,而且有十分重要的应用参考价值。
1 问题描述
飞行器控制一般可以分为内回路设计与外回路设计。外回路是在内回路稳定设计的基础上,对飞行器的质心加以控制。因此内回路是飞行器稳定至关重要的核心回路。近年来,由于飞行器速度的增大,以及控制精度要求的提高,尤其是攻角测量与传感技术的发展,基于攻角可测的攻角稳定回路设计,也具有越来越重要的工程应用价值。
本文是基于以上背景,采用攻角传感器与陀螺仪,测量飞行器的攻角与俯仰姿态角速度,并构造一类同步系统,实现在气动参数强不确定环境下的飞行器的攻角跟踪控制。
按照传统飞行器设计的特征点固化线性化思想,可以得到飞行器在某一特征点附近的线性化模型,该模型为二阶系统,如下所示:
(1)
(2)
其中,aij为空气动力学参数。滑模控制的目标为设计滑模控制器,使得导弹攻角α跟踪期望值αd。
2 PID控制律设计
图1所示为PID控制系统的结构图,该系统由PID控制器和被控对象两部分组成,PID控制器产生的控制信号对被控对象进行控制。其中PID控制器由比例(P)、积分(I)和微分(D)三个环节组成。

图1 PID控制系统结构图Fig.1 Structure of PID control system
PID控制器是一种线性控制器,它根据给定期望值αd与实际输出值α构成控制偏差
e(t)=α-αd
(3)
PID的控制规律为
(4)
写成传递函数的形式为
(5)
式中:kp为比例系数;TI为积分时间常数;TD为微分时间常数。
3 滑模控制律设计
假设:期望值αd为常值,其导数为0。
滑模控制系统的设计通常被认为是一种综合方法,特点是简单、灵活。设计滑模控制系统的基本步骤,包括两个相对独立的部分:
1)设计滑模函数s(x),使它所确定的滑动模态渐近稳定且有良好的品质。
2)求出滑模控制u(x),使系统满足滑模到达条件,从而形成滑动模态。
这样,滑模控制既保证趋近运动在有限时间内到达滑模面,又保证了滑模面是滑动模态区。一旦滑模函数s(x)和滑模控制u(x)都得到了,滑模控制系统就完全建立起来了。
定义误差变量e=α-αd,则有
(6)
误差二阶导数为
(7)
对于误差模型关键是如何消除误差,采用滑模控制器可以达到消除误差的作用。首先定义滑模面如下
(8)
为保证滑模面有意义,当滑模面等于0时,微分方程稳定,则有c1>0,c2>0。
然后求取滑模面的导数得
(a22-a34+c1)ωz+
(9)
定义:
(10)
l2=a22-a34
(11)
l3=c2
(12)
定义
(13)
设计
(14)
其中,k1、k2、k3为控制器参数。
定义:
(15)
(16)
(17)
则有
(18)
即
(19)
即
k1s2-k2sgn(s)s
(20)
定义权值调节规律如下:
(21)
(22)
(23)
其中,Γ1、Γ2、Γ3为权值调节参数。
选取Lyapunov函数
(24)
求导得
(25)
选取Lyapunov函数
(26)
则有
k1s2-k2sgn(s)s
(27)
选取系统总Lyapunov函数为
V=V1+V2
(28)
求取其导数得
(29)
可见系统在滑模控制的作用下是稳定的,而且并不需要系统的增益为较大值。
4 仿真分析
本文采用超声速导弹在某一特征点的气动参数进行仿真分析说明,气动参数取值如下:
a25=-167.87;a35=0.243;a22=-2.876;
a24=-193.65;a34=1.584
由于导弹在数字仿真中采用的气动数据为风洞吹风所得数据插值所得。因此导弹实际飞行中气动数据可能和仿真中数据有差别,因此我们在特征点附近采用将全部气动数据上下摄动50%甚至500%来验证所设计的控制器的鲁棒性。
4.1PID控制仿真结果
以选取超声速导弹特征点为被控系统参数,经过多次仿真并修改控制参数,最后选取控制器参数如下:
kp=2,ki=5,kd=5
首先在无参数摄动情况下进行仿真,可以得到如图2所示仿真结果。
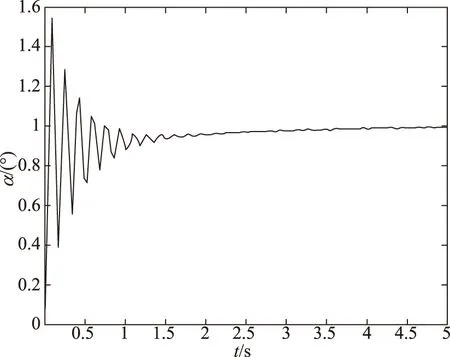
图2 PID仿真结果Fig.2 Simulation result of PID control
然后考虑有参数摄动的情况。设固定摄动量k,此时摄动后弹体参数为:
A22=a22(1+k);
A24=a24(1+k);
A25=a25(1+k);
A34=a34(1+k);
A35=a35(1+k)。
信号期望均为1,如图3~图8所示仿真结果。
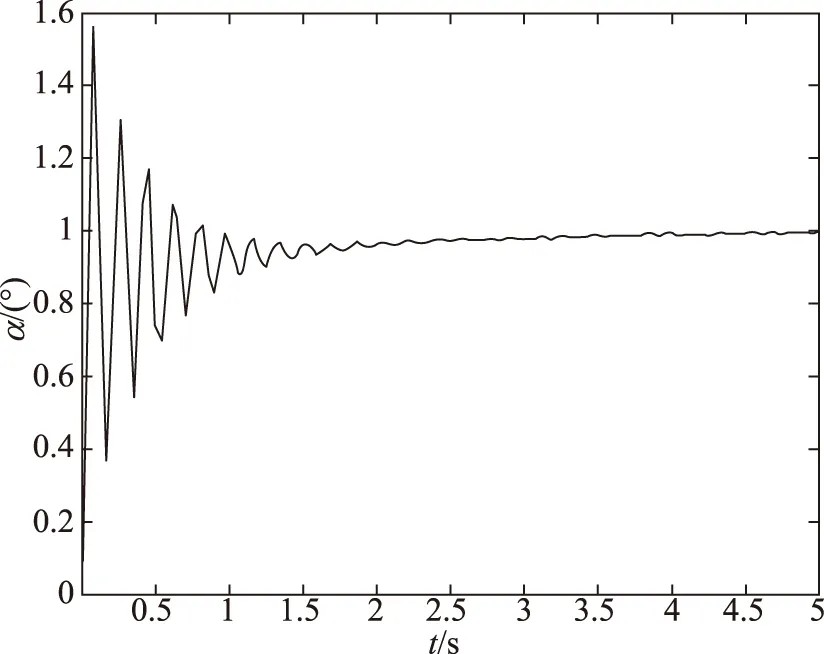
图3 k=-10%时仿真结果Fig.3 The result of k=-10%
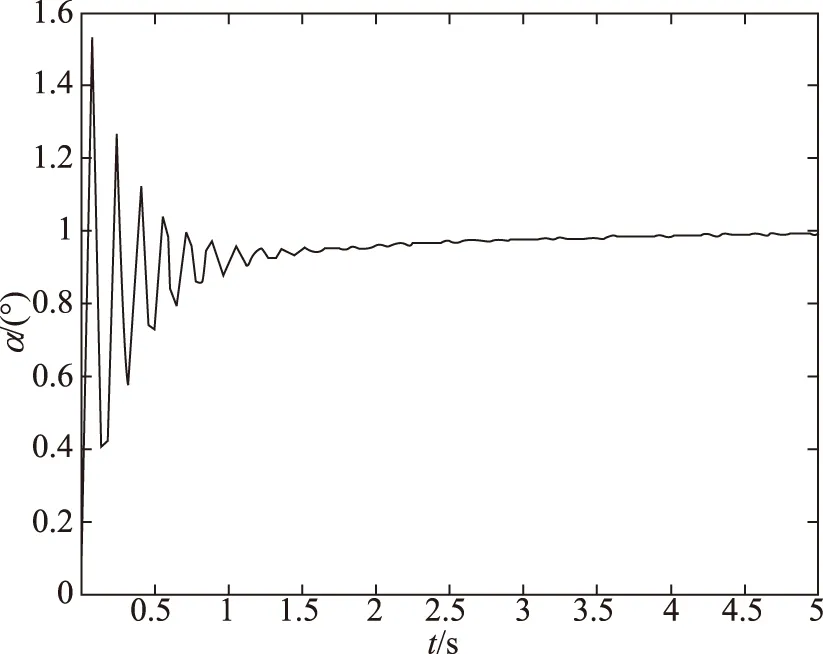
图4 k=10%时仿真结果Fig.4 The result of k=10%
设随机摄动量为KS,由于该摄动量为随机量,在选取随机数值时本文采用MATLAB中rand函数指令,可得随机摄动量的表达式为
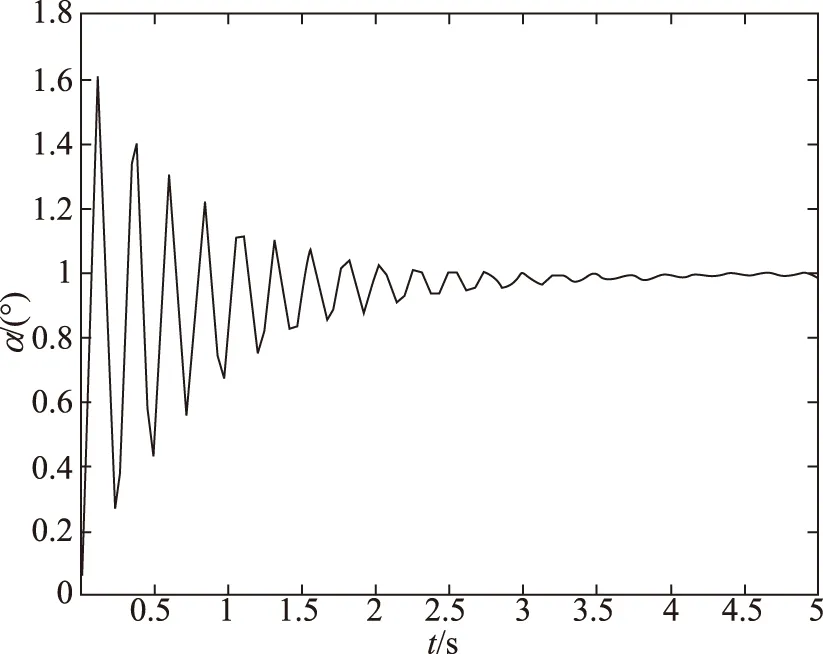
图5 k=-50%时仿真结果Fig.5 The result of k=-50%
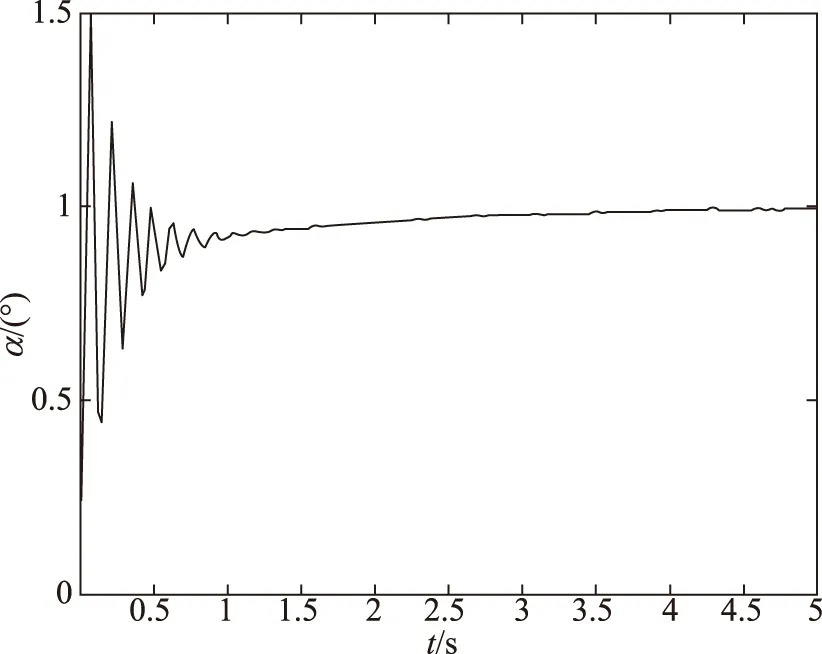
图6 k=50%时仿真结果Fig.6 The result of k=50%

图7 k=-90%时仿真结果Fig.7 The result of k=-90%
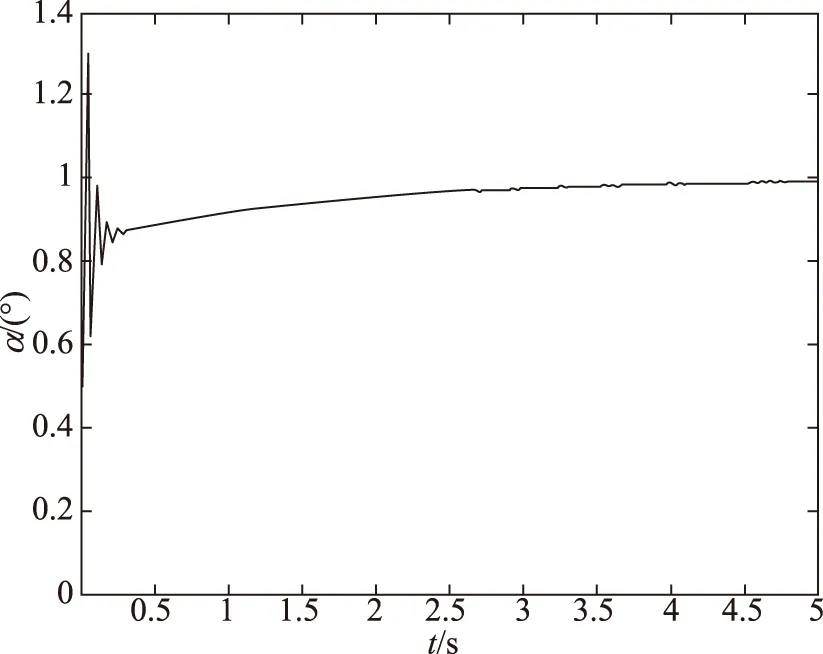
图8 k=500%时仿真结果Fig.8 The result of k=500%
ks=2K·(rand(5,1)-0.5)
(30)
其中变量rand函数表示一范围(0,1)的随机数值,K为随机摄动量范围的绝对值,在MATLAB软件中每执行一次该函数指令都可以产生相应摄动范围内的5个随机数,即ks1、ks2、ks3、ks4、ks5。
此时,摄动后弹道参数为:
A22=a22(1+ks1);A24=a24(1+ks2);
A25=a25(1+ks3);A34=a34(1+ks3);
A35=a35(1+ks5)
可以得到如图9~图12所示仿真结果。
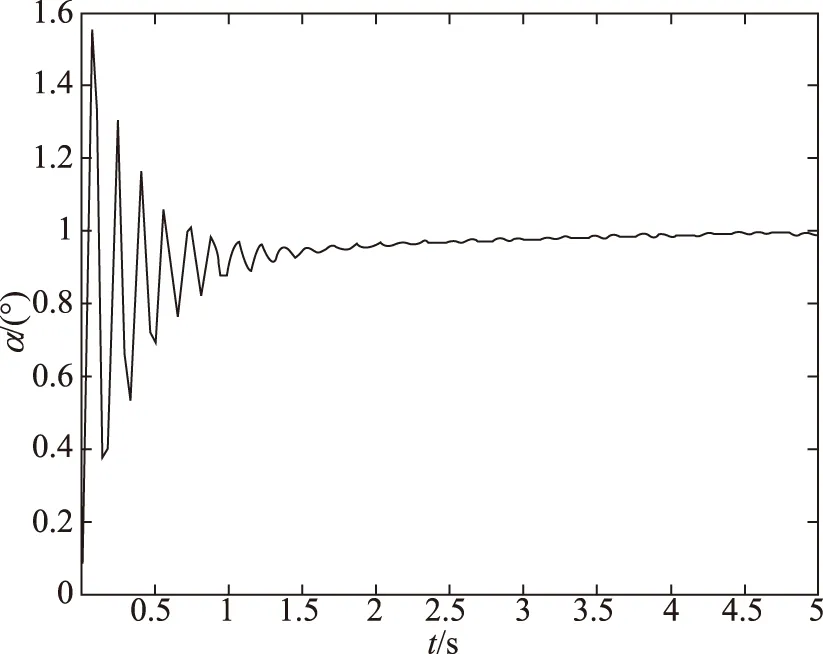
图9 ks∈(-10%,10%)时仿真结果Fig.9 The result of ks∈(-10%,10%)
仿真结果表明,在较小范围的扰动下,采用PID控制可以保证系统的稳定。但是当扰动范围变大,特别是负扰动的情况下,系统会出现不稳定,并且有较大的震荡。
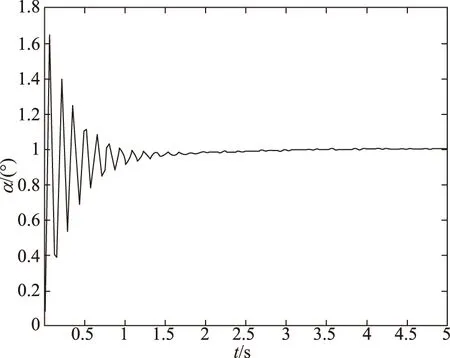
图10 ks∈(-50%,50%)时仿真结果Fig.10 The result of ks∈(-50%,50%)
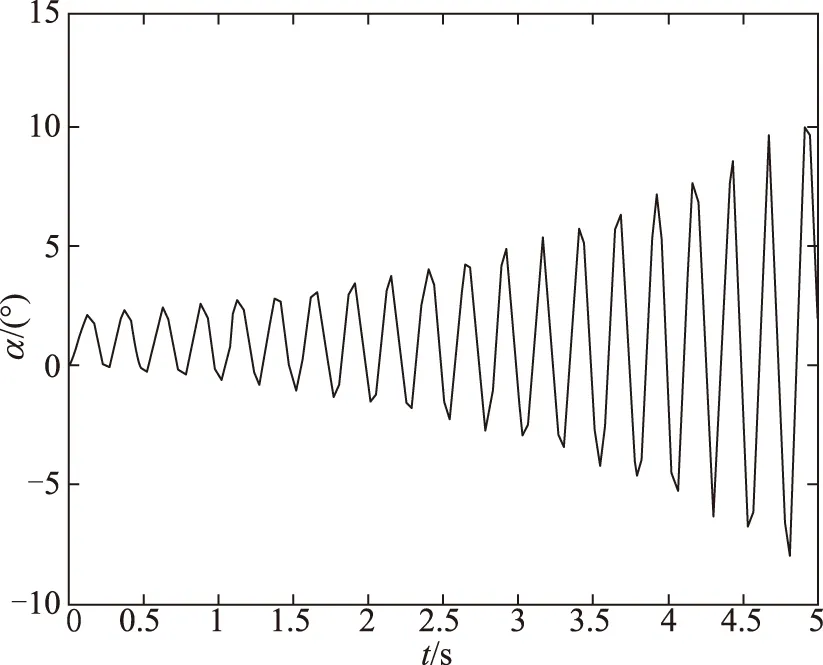
图11 ks∈(-90%,100%)时仿真结果Fig.11 The result of ks∈(-90%,100%)

图12 ks∈(-90%,500%)时仿真结果Fig.12 The result of ks∈(-90%,500%)
4.2 滑模控制仿真结果
选取控制器参数如下:
c1=8,c2=5,Γ1=1,Γ2=1,Γ3=1,
k1=20,k2=20,k3=20
首先在无参数摄动情况下进行仿真,可以得到如图13所示仿真结果。

图13 滑模控制仿真结果Fig.13 The result of sliding mode
然后按照PID固定参数摄动的方法进行仿真,可以得到如图14~图19所示仿真结果。

图14 k=-10%时仿真结果Fig.14 The result of k=-10%
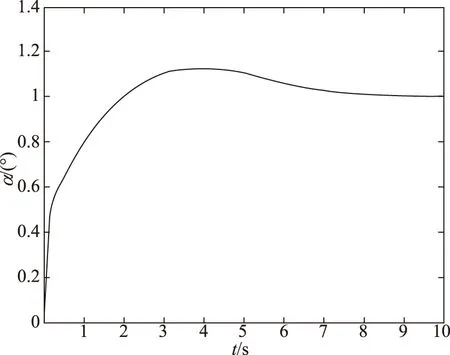
图15 k=10%时仿真结果Fig.15 The result of k=10%
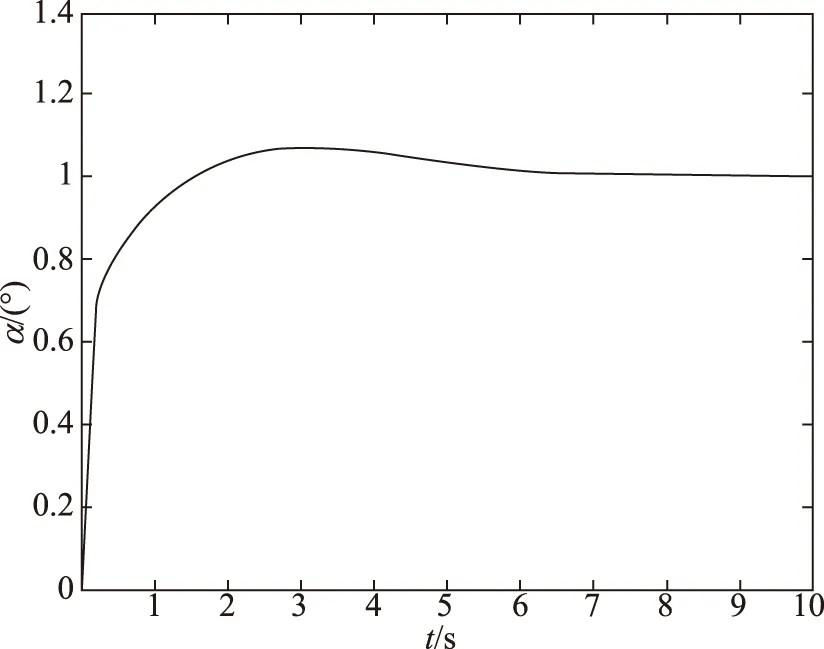
图16 k=-50%时仿真结果Fig.16 The result of k=-50%
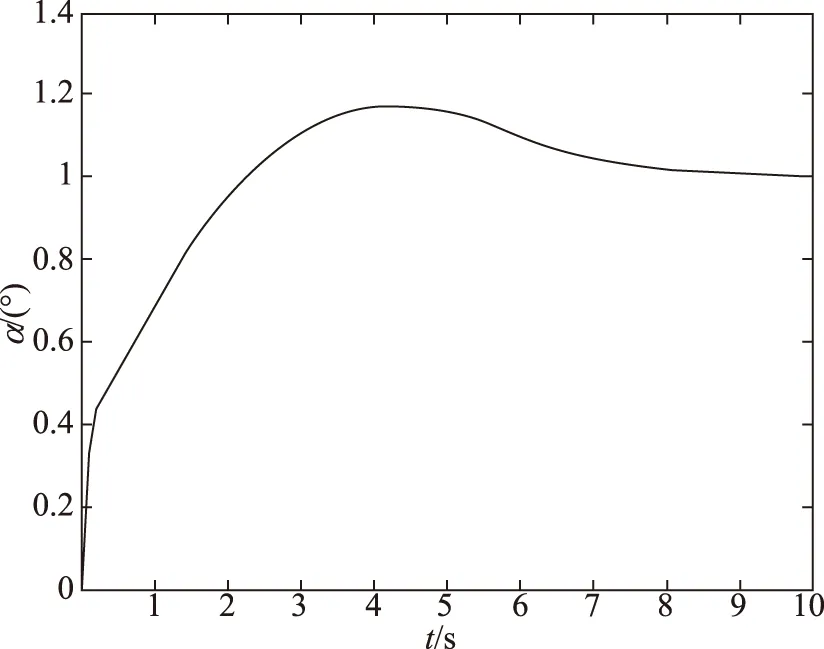
图17 k=50%时仿真结果Fig.17 The result of k=50%

图18 k=-90%时仿真结果Fig.18 The result of k=-90%
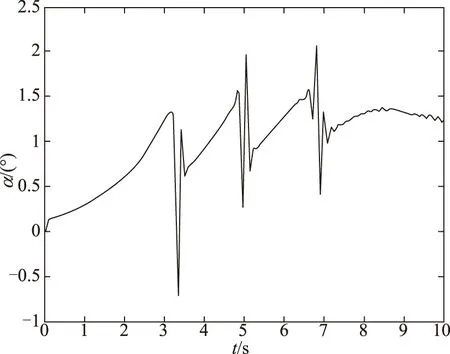
图19 k=500%时仿真结果Fig.19 The result of k=500%
最后按照PID随机参数摄动的方法进行仿真,可以得到如图20~图23所示仿真结果。
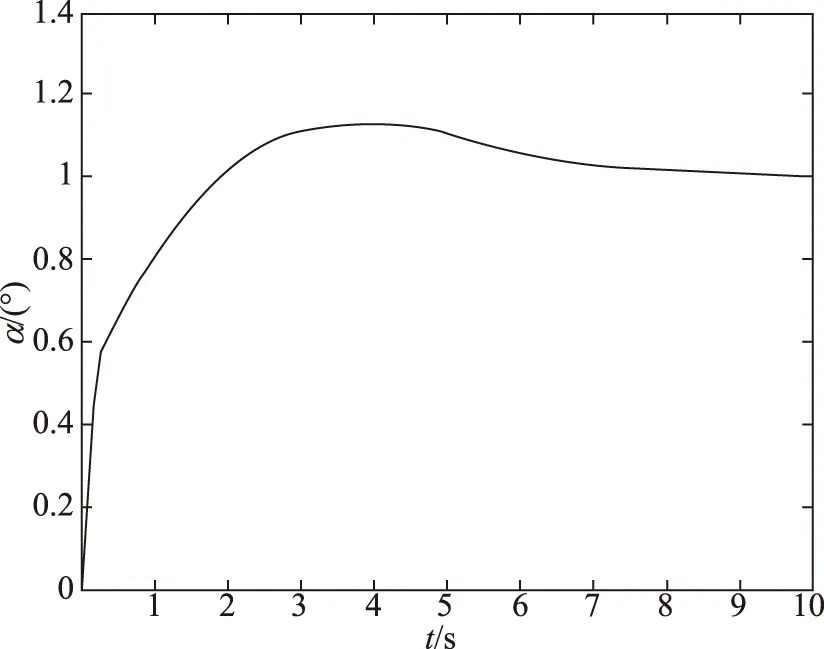
图20 ks∈(-10%,10%)时仿真结果Fig.20 The result of ks∈(-10%,10%)
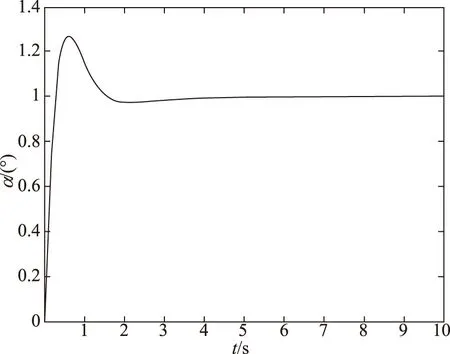
图21 ks∈(-50%,50%)时仿真结果Fig.21 The result of ks∈(-50%,50%)
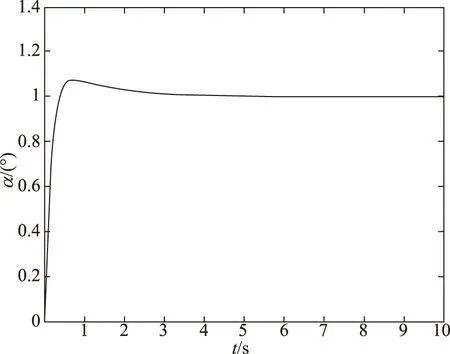
图22 ks∈(-90%,100%)时仿真结果Fig.22 The result of ks∈(-90%,100%)
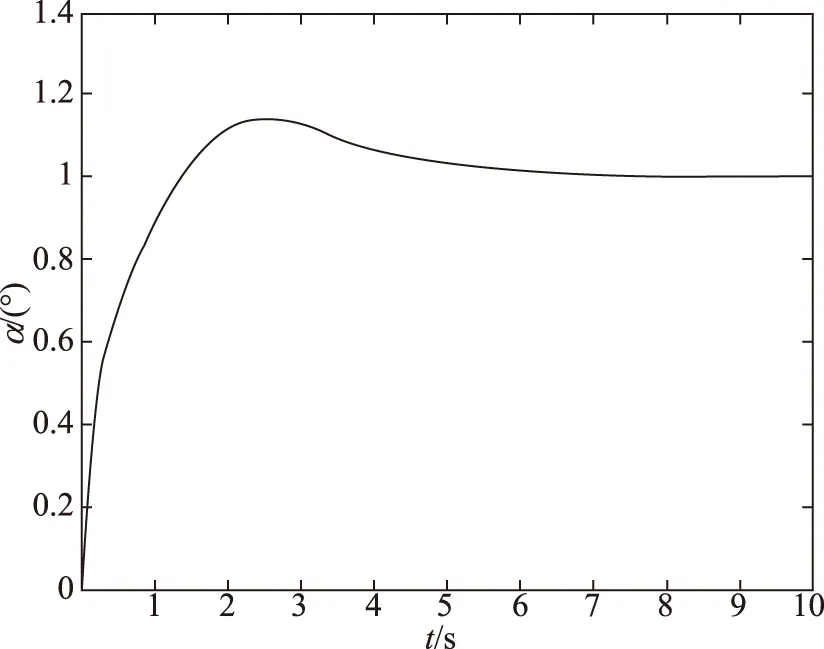
图23 ks∈(-90%,500%)时仿真结果Fig.23 The result of ks∈(-90%,500%)
仿真结果在不同的摄动情况下都稳定,说明了该控制方法有较强的鲁棒性。
4.3 对比与分析
通过对比PID控制方法可以知道,采用两种不同的控制方法都可以使被控系统在选取的特征点稳定,并且在小范围的参数摄动下仍然保持稳定,但是在较大范围的参数摄动情况下,采用PID控制的系统较采用滑模方法控制的系统控制效果较差一些。尤其是当参数摄动为随机摄动时,采用PID控制的系统与采用滑模控制的系统存在着一定差距。
由此可以得出结论:在控制模型参数确定的情况下,PID和滑模两种控制方法都有不错的控制效果,但是PID控制的系统的鲁棒性要略差于滑模控制的系统,当被控系统的数学模型不确定或者变化较大时,采用滑模法控制的效果要优于PID控制。
5 结束语
由于传统的PID控制方法需要知道被控系统的标称数学模型,但是超声速导弹模型具有时变、不确定等特点,采用PID控制效果并不能保证所有情况均有理想的控制性能。所以针对简化的超声速导弹模型,本文提出了一种滑模控制方法,并对比了两种控制方法在不同参数摄动情况下的控制效果,发现参数变化范围较大的情况下,滑模控制方法效果要远远优于PID控制方法。这表明采用滑模法控制时,可以在并不精确地知道二阶系统模型参数的情况下,依然获得不错的控制效果,使系统具有较好的鲁棒性。由此采用滑模法设计的控制系统在模型参数时变、不确定的超声速导弹中会有较好的应用前景。
[1] 袁赣南,左志丹,曲桂婷,纪红.二阶滑模变结构控制系统的滑模到达条件[J].华中科技大学学报,2013(6):70-75.
[2] 袁赣南,左志丹,孙宁博.基于趋近律的二阶滑模变结构控制[J].系统工程与电子技术.
[3]ShtesselYB,ShkolnikovIA,LevantA.Guidanceandcontrolofmissileinterceptorusingmodes[J].IEEETransactionsonAerospaceandElectronicSecond-OrderSlidingSystems,2009,45(1):110-124.
[4]DuanChao-yang,ZhangYing-xin.Adaptiveslidingmodecontrolforbank-to-turnmissiles[C]//.The9thIEEEInternationalConferenceonElectronicMeasurement&Instruments,2009,3:512-517.
[5] 王志,周军,周凤岐.低速滚转导弹弹道导弹运动模型及变结构姿态控制系统设计[J].兵工学报,2007,28(7):849-853.
[6]CastilloTB,CastroLR.Onrobustregulationviaslidingmodefornonlinearsystems[J].System&Controlletters,1995,24:361-371.
[7]ShtesselY,HallC,JacksonM.Reusablelaunchvehiclecontrolinmultiple-tmie-scaleslidingmodes[J].JournalofGuidance,ControlandDynamics,2000,23(6):1013-1020.
[8]XuH,MirmiranniMD,IoannouPA.Adaptiveslidingmodecontroldesignforahypersonicflightvehicle[J].JournalofGuidance,ControlandDynamics,2004,27(5):829-838.
[9]SepulchreR,JankovicM,KokotovicPV.Constructivenonlinearcontrol[M].NewYork:Springer,1997.
[10]JankovicM,FontaineD,KokotovicPV.Constructivelyapunovstabilizationofnonlinearcascadesystems[J].IEEETransactiononAutomaticControl,1996,41(12):1723-1735.
[11]JiangZP,PralyL.Robustadaptivecontrollersfornonlinearsystemswithdynamicuncertainty[J].Automatica,1998,34(7):825-840.
[12]QianChun-jiang,WeiLin.Non-Lipschitzcontinuousstabilizersfornonlinearsystemswithuncontrollableunstablelinearization[J].Systems&ControlLetters,2001,42:185-200.
Research on Sliding-mode Control Based on Uncertain Simplified Model of Supersonic Missile
JIN Yu-qiang,LI Ze-xue,LEI Jun-wei
(Naval Aeronautical and Astronautical Engineering University,Yantai 264001,China)
Based on the uncertain supersonic missile simplified model parameters that are time-varing and uncertain,this article focuses on the research of sliding-mode control.Through the theoretical analysis and the simulation,it is proved that the sliding mode control for the uncertain system has a better control effect.And compared with the PID control method,sliding mode control has better robustness.The validity of the sliding mode control of uncertain supersonic missile is proved.
Uncertain supersonic missile;Sliding mode control;PID control
2015-05-07;
2015-09-10。
晋玉强(1977-),男,副教授,硕士生导师,主要从事导航制导与控制方面的工作。
TM273
A
2095-8110(2016)02-0025-08

