基于区间数和改进灰色证据理论的地铁绿色施工方案评价

许秀娟，王　蕾

(广东科学技术职业学院， 广东 广州 510640)



基于区间数和改进灰色证据理论的地铁绿色施工方案评价

许秀娟，王蕾

(广东科学技术职业学院， 广东 广州 510640)

摘要：针对地铁绿色施工方案指标值以区间数形式给出的多指标决策问题，提出了一种基于区间数和改进灰色证据理论的评价方法。该方法以灰色关联系数得到指标的不确信度，从而构建多指标下备选方案的Mass函数矩阵，通过证据理论的Dempster合成法则对Mass函数进行信息融合，根据得到的信度函数值对方案进行排序。该方法舍弃区间数权重的计算，同时对灰色关联系数、不确定度和理想偏离度等作出改进，使得计算过程和结果更为简便有效。最后结合实例进行了验证计算，结果表明该方法能够最大程度地消除评价对象内在的不确定性，切实可行，评价过程简洁直观。

关键词：绿色施工方案；证据理论；灰色关联；区间数

随着加强生态文明建设、促进城市可持续发展理念的不断深入，倡导绿色施工，走绿色建筑之路，已经逐渐成为建筑业的发展方向，对于我国经济增长方式由粗放型向集约型转变有着重要意义[1]。《建筑工程绿色施工评价标准》[2](GB/T 50640-2010)、《建筑工程绿色施工规范》[3](GB/T 50905-2014)等标准和规范的颁布实施，让绿色施工逐渐走向了标准化道路，因此在现有标准的基础上，对绿色施工方案进行评价优选是实现绿色施工的重要手段，国内外学者利用层次分析法、模糊综合评价、价值工程等方法或手段对绿色施工方案进行优劣评价。如邓朗妮等[4]针对施工方案功能条件及成本构成较复杂而难以评价的施工方案，提出了基于价值工程的绿色施工方案评价。晋良海等[5]建立了绿色施工方案评价的有序加权几何平均算子(OWGA算子)和组合加权几何平均算子(CWGA算子)集成方法。焦艳彬等[6]利用德尔菲法建立土石方调配绿色施工评价体系，将层次分析法与模糊综合评价法相结合用来确定土石方调配方案的绿色施工等级。卢颖等[7]引入联系数理论将指标区间数矩阵转化为联系数矩阵，建立了基于联系数的区间多属性地铁绿色施工方案评价模型。

作为一种独立的有轨交通系统，地铁具有用地集约、效率高、能耗低、无污染等众多优点，具有良好的社会效益。然而地铁大都为地下结构物，且施工过程中涉及到绿化迁移、交通疏散、房屋拆迁、管线迁改等众多因素，是一个复杂的系统工程，因此地铁绿色施工方案具有施工复杂、隐蔽性大、未知不确定性因素多等特点。本文用区间数来表示评价指标数值，在王育红等[8-10]众多学者的研究成果基础上，将灰色关联和证据理论相结合应用于地铁绿色施工方案区间数评价中。首先区分效益型指标和成本型指标确定规范化决策矩阵，在此基础上，通过灰色关联系数得到指标的不确信度，从而构建Mass函数，最后利用证据理论对Mass函数进行融合得到信度函数值，以此为地铁绿色施工方案排序。本文在已有研究的基础上，做出如下改进：舍弃区间数权重的计算，因灰色关联系数得到的不确定度已经包括权值信息；仅使用最优关联系数求取不确定度，因最优和最劣关联系数的计算并不能带来更精确的关联度；使用灰色关联系数的积表示不确定度，因关联系数求和不确定度逻辑上不对等；另外，本文理想偏离度通过指标的最劣值来求取，可以避免零值的出现，使得证据合成规则对所有区间数数值有效。

1基本理论

1.1区间数的基本知识

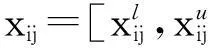
(1)

当p=1时，两个区间数的海明距离为：

(2)

当p=2时，两个区间数的欧氏距离为：

(3)

当Dp(x1，x2)=0时，两个区间数相等，Dp(x1，x2)越大，说明两个区间数的相离度越大。海明距离一般用于相似度的计算，而欧氏距离能更好地表达m维空间中两个点之间的真实距离，因此，本文在计算时采用欧式距离，取p=2。区间数x1≥ x2的可能度为：

(4)

1.2灰色关联理论

灰色关联理论是我国著名学者邓聚龙教授提出的一种系统科学理论。灰色关联分析的基本思想是根据参考数据列与比较数据列的曲线几何形状相似程度来判断其联系的紧密程度[11]。灰色关联度计算方法如下：

首先计算绝对关联度，设初始行序列Xi=(xi1，xi2，…，xit)计算其零化象，

(5)

令

(6)

(7)

则子系统ij间的绝对关联度为

(8)

μij介于0到1之间，数值越大表示关联程度越高，越小则越低。

1.3D-S证据理论

D-S证据理论基于人们对不确定性事件给出的不确定性度量，是一种不确定性推理融合算法。它利用证据的积累，不断地缩小假设集，对矛盾信息进行删除、重新整合，最后得到结论[12-13]。

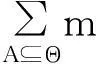
D-S证据理论的结论表达对任意一个假设的支持力度，则称Bel:2Θ→[0，1]为Θ上对应m的信度函数，识别框架Θ上定义的信度函数为：

(9)

应用证据理论的Dempster合成规则，合成后的Mass函数如式(10)：∀B，C⊆Θ，

m(A)=mi(B)⊕mj(C)=

(10)

对于∀A⊆Θ，证据m1，m2，…，mn为识别框架Θ下的Mass函数，则两个以上Mass函数合成规则如式(11)：

(m1⊕m1⊕…⊕mn) (A)=

(11)

证据理论合成公式有两个重要特征：交换性和结合性[14]。表述如下：

(1) m1⊕m2=m2⊕m1；

(2) m1⊕(m2⊕m3)=(m1⊕m2)⊕m3。

2地铁绿色施工方案评价

2.1区间数规范化和实数化

地铁绿色施工方案评价指标xij构成的初始区间决策矩阵X=(xij)m×n，要采用D-S证据理论对施工方案进行评价，需要对初始区间决策矩阵进行规范化处理。将指标分为效益型指标和成本型指标。对于效益型指标：

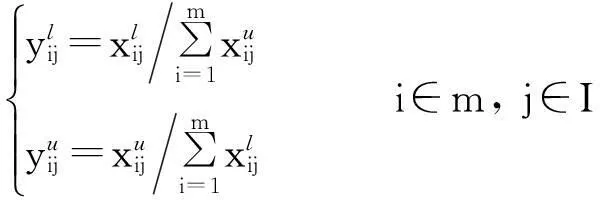
(12)

对于成本型指标：

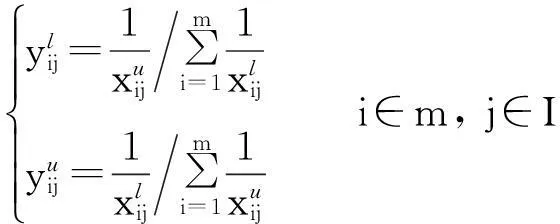
(13)

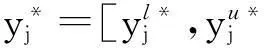
2.2改进的灰色关联法确定Mass函数

通过求解指标的不确信度来计算Mass函数，在此基础上利用证据理论进行信息合成。因此，本文首先以灰色关联法来计算指标的不确信度。从本质上看，灰色关联所得系数表示的是与参考指标的相关程度，所以本文以最优理想区间为参考序列，得到与最优序列的关联系数。灰色关联系数求取如下式(14)所示：

(14)

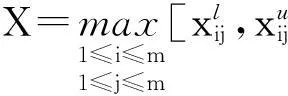
若各指标与最优理想区间的关联度都相近，则该指标对决策带来更大的不确定度，故证据理论的不确定度以单个指标下的关联系数乘积意义更明确，其定义如下：

(15)

进而可以计算各指标的基本概率分配(Mass函数)：

(16)

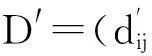
(17)

2.3综合评价流程

综上所述，可得到基于区间数和改进灰色证据理论的地铁绿色施工方案评价步骤如下：

(2) 根据Y求出最优理想序列，通过公式(14)确定最优关联系数矩阵，进而由公式(15)得到指标下的不确信度DOI(Ij)。

(3) 求出区间数偏离度距离矩阵D，进而可得归一化偏离度矩阵D′。

(4) 运用公式(16)计算Mass函数mj(i)，在此基础上得到整体不确定的Mass函数mj(i+1)。

(5) 应用Dempster合成法则对Mass函数进行合成，根据信度函数最大化原则对备选方案进行排序。

3算例分析

目前我国尚未形成统一的地铁绿色施工方案评价指标体系。本文以相关的绿色建筑、绿色施工国家标准规范为基础，结合相关绿色施工方案专家意见及地铁绿色施工特征，得到地铁绿色施工方案6个主要评价指标分别为：(1) I1：绿色施工管理制度和体系；(2) I2：运用绿色施工新技术、新工艺；(3) I3：“三废”排放与控制；(4) I4：专项工程重大环境因素防治；(5) I5：节能与能源利用；(6) I6：资源回收与再利用。为与文献[7]的结果相比较，本文仍以南方某城市地铁X号线为例，全长25.38km，共21个区间、18座明挖车站和4座盖挖车站，其中换乘站9座，采用明挖法、矿山法和盾构法进行施工。共有A1、A2、A3、A4四个施工方案，经专家打分，各地铁绿色施工方案初始值如表1所示。

根据前文公式(12)和(13)对初始值进行规范化处理，得到规范后的各方案指标值如表2所示。

通过对各个区间数的距离判断，找出最优理想区间序列，运用公式(14)求出灰色关联系数矩阵R。

表1　各地铁绿色施工方案初始值[7]

方案不同指标下地铁初始值I1I2I3I4I5I6A1[75.0,78.3][86.6,88.7][66.9,72.3][76.8,84.5][71.0,80.5][66.9,80.5]A2[77.6,85.6][83.2,90.2][68.8,73.4][85.2,88.2][72.3,78.5][77.7,82.5]A3[82.0,87.6][78.9,85.9][77.5,85.9][69.3,78.9][81.2,90.0][86.0,94.3]A4[76.9,81.0][77.5,85.0][67.2,74.6][83.1,85.9][68.9,76.8][71.3,79.5]

表2　规范后的各方案指标值

得到指标Ij下的信息不确定度分别为：DOI(I1)=0.6745；DOI(I2)=0.6878；DOI(I3)=0.5018；DOI(I4)=0.6498；DOI(I5)=0.5216；DOI(I6)=0.4785。

根据本文的理想区间数定义，可得到理想区间[75.0，75.0][77.5，77.5][66.9，66.9][69.3，69.3][68.9，68.9][66.9，66.9]，通过计算理想偏离度，得到归一化的理想度矩阵D′为：

根据基本概率分配公式，得到绿色施工方案的Mass函数矩阵为：

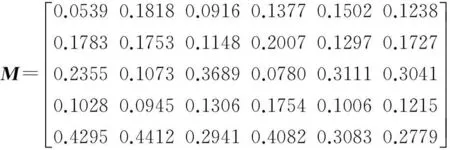
利用上述方案的Mass函数矩阵，可得整体不确定性Mass函数分别为：m1(6)=0.4295；m2(6)=0.4412；m3(6)=0.2941；m4(6)=0.4082；m5(6)=0.3083；m6(6)=0.2779。令辨识框架Θ={A1,A2,A3,A4}，并取2Θ={{A1},{A2},{A3},{A4},{A1,A2,A3,A4}}，通过Dempster合成法则，得到合成后Θ内各子集的信度函数分别为：

bel(A1)=(m1⊕m2⊕m3⊕m4⊕m5⊕m6)

(A1)=0.1358

bel(A2)=(m1⊕m2⊕m3⊕m4⊕m5⊕m6)

(A2)=0.2142

bel(A3)=(m1⊕m2⊕m3⊕m4⊕m5⊕m6)

(A3)=0.4930

bel(A4)=(m1⊕m2⊕m3⊕m4⊕m5⊕m6)

(A4)=0.1323

bel(A1，A2，A3，A4)=(m1⊕m2⊕m3⊕m4⊕m5⊕m6)(A1，A2，A3，A4)=0.0227

根据信度函数最大化原则，可得到4个绿色施工方案的排序为：A3>A2>A1>A4，决策者在风险中性的态度下应选择最优方案A3，其次为方案A2，与文献[7]应用联系数理论优选结果相一致。同时，可以发现在信息合成过程中，整体不确定性的信度函数值降低到融合后的2.27%，该过程降低了信息的不确定度，从而根据信度函数值能较客观地做出有效评价。

4结论

本文将改进的灰色证据理论应用于地铁绿色施工方案区间数评价中。通过灰色关联系数得到指标的不确信度，从而构建Mass函数，最后利用Dempster合成法则对Mass函数进行融合得到信度函数值，以此为地铁绿色施工方案排序。此外本文在已有研究的基础上，做出如下改进：舍弃区间数权重的计算，以灰色关联系数求出的不确定度已经包括权值信息；仅使用最优关联系数使计算过程更为简便；以灰色关联系数的积表示不确定度以及通过指标的最劣值来求取理想偏离度。实例结果表明该方法切实可行，降低了整体不确信度，评价过程更为简洁直观，有利于地铁绿色施工在我国的推广和发展。

参考文献：

[1]闫志刚，杜立峰，王雪丽．基于突变级数法的绿色施工评价研究[J]．施工技术，2012，41(21)：25-29．

[2]中华人民共和国住房和城乡建设部．建筑工程绿色施工评价标准:GB/T50640-2010[S].北京：中国计划出版社，2010．

[3]中华人民共和国住房和城乡建设部．建筑工程绿色施工规范:GB/T50905-2014[S].北京：中国建筑工业出版社，2014．

[4]邓朗妮，黄如寤．基于价值工程的绿色施工方案评价[J]．施工技术，2007，36(S1)：449-451．

[5]晋良海，薛晓飞，郝胜，等．绿色施工方案评价的OWGA和CWGA集成方法[J]．水利水运工程学报，2013(4)：35-39．

[6]焦艳彬，赵春菊，周宜红，等．基于绿色施工的堆石坝土石方调配方案评价[J]．水电能源科学，2013，31(11)：163-167．

[7]卢颖，谢红涛，李波，等．基于区间数属性联系度的地铁绿色施工方案评价[J]．施工技术，2015，44(5)：107-110．

[8]王育红，党耀国．基于灰色关联系数和D-S证据理论的区间数投资决策方法[J]．系统工程理论与实践，2009，29(11)：128-134．

[9]许秀娟，牟浩．基于结构熵权灰色关联和D-S证据理论的水库兴利调度综合评价[J]．水利与建筑工程学报，2014，12(2)：21-25．

[11]李海东，王帅，刘阳．基于灰色关联理论和距离协同模型的区域协同发展评价方法及实证[J]．系统工程理论与实践，2014，34(7)：1749-1755．

[12]ShaferG.AmathematicalTheoryofEvidence[M].NewJersey：PrincetonUniversityPress，1976．

[13]BaeHR,GrandhiRV,CanfieldRA.Sensitivityanalysisofstructuralresponseuncertaintypropagationusingevidencetheory[J].StructuralandMultidisciplinaryOptimization, 2006,31(4)：270-279．

[14]李存斌，赵坤，苑嘉航．改进灰色证据理论的区间数决策方法研究[J]．天津工业大学学报，2014，33(4)：70-75．

Evaluation of Green Subway Construction Scheme Based on Interval Number and Improved Gray correlation and D-S Theory of Evidence

XU Xiujuan， WANG Lei

(GuangdongInstituteofScienceandTechnology,Guangzhou,Guangdong510640,China)

Abstract：Green subway construction program is of a good way to achieve standard green subway construction. Focusing on solving the decision problems with multiple attribute which is given by interval numbers, an evaluation method based on Interval Number was proposed. This method obtain the uncertainty of Indicators by gray correlation coefficient to construct matrix of Mass function on Alternative with multi-index, we can then use the combination rule of D-S theory to synthesis the Mass Function and get the best result based on the principle of maximizing the reliability function.This method discards weight calculation of interval numbers, and at the same time makes improvements on Grey correlation coefficient, uncertainty and ideal deviation to make the calculation process more simple and effective. An example was calculated using the proposed method, the results show that this method is practical, simple and intuitive as it eliminates the uncertainty of information.

Keywords:green construction scheme； theory of evidence； gray correlation； interval number

文章编号：1672—1144(2016)01—0202—05

中图分类号：U455

文献标识码：A

作者简介：许秀娟(1988—)，女，四川资阳人，硕士研究生，研究方向为项目可行性研究及项目管理。 E-mail：xuxiujuanlu@163.com

收稿日期：2015-09-25修稿日期：2015-10-22

DOI:10.3969/j.issn.1672-1144.2016.01.038