关于考虑弯曲刚度的斜索面内自由振动解的注记

肖　一

(1.福建工程学院 土木工程学院， 福建 福州 350118；

2.福建省土木工程新技术与信息化重点实验室， 福建 福州 350118)



关于考虑弯曲刚度的斜索面内自由振动解的注记

肖一1，2

(1.福建工程学院 土木工程学院， 福建 福州 350118；

2.福建省土木工程新技术与信息化重点实验室， 福建 福州 350118)

摘要：对索的准确模拟应考虑弯曲刚度的影响。关于考虑弯曲刚度的斜索面内自由振动，目前只有两端铰接边界条件下的解析解，这与实际拉索的边界条件不相符。在已有研究基础上，对考虑弯曲刚度的斜索面内自由振动解析解在中点割线坐标系下进行了推导，补充了两端固接条件下的解。分析结果表明斜索无Crossover现象，其振型为非对称，考虑弯曲刚度的频率要大于不考虑弯曲刚度的频率，两端固接频率大于两端铰接频率。通过对比认为考虑弯曲刚度影响在某些情况下是必要的；应该考虑不同边界条件的影响；由于理想边界的上下界性质，利用文中结果可以对实际情况进行估计和近似。

关键词：斜索；自由振动；弯曲刚度；解析解

现代索支撑桥梁跨径的不断增大使得索的直径越来越大，如明石海峡大桥和青马大桥的主缆直径已达1.1 m[1]，正在修建的墨西哥海峡大桥的主缆直径则近1.2 m[2]。对于大直径索而言，为了更准确地分析结构的动力响应，一般应计入弯曲刚度的影响。另外，振动法测索力的方法[3-5]中几乎毫无例外地均考虑了弯曲刚度对拉索自振频率的影响。

最近，文献[6]在其已有研究[7]的基础上考虑了弯曲刚度影响推导了斜索面内自由振动解析解，但其仅考虑了两端铰接边界条件。文献[2]在关于考虑弯曲刚度的水平索的推导中则仅考虑了两端固接条件。仅就斜拉桥而言，从文献[8]可知，斜拉索两端可能有多种锚固形式，从而对应不同的边界条件。采用数值方法时[1，9]，一般对两种情况均进行了分析。

本文在文献[6]的基础上在改进坐标系下补充了该问题在两端固接情况下振型和频率解析解，并重新给出了两端铰接时的解，讨论表明了该补充的必要性。

1理论推导

在索振动分析中，已有的文献多将坐标原点置于端点处[6-7,10-11]，这对于求解一般索及计入弯曲刚度的两端铰接索时是比较方便的，但对于两端固结时，其求解过程非常复杂，且很难获得最简形式。

在求解考虑弯曲刚度水平索的自由振动问题时，文献[2]考虑到索构形和边界条件的对称性将坐标原点置于弦的中点，这使得其直接利用了该对称性简化了求解。本文讨论的斜索虽然没有对称轴，但边界条件具有对称性，若将坐标原点置于弦中点处，利用三角函数的奇偶性，也将使求解过程大为简化，尤其对于两端固接的情况。

在图1所示中点割线坐标系Oxz下，考虑弯曲刚度的索面内线性运动方程为[2,6]：

(1)

式中：x和z为原点位于弦中心的割线坐标系的两个坐标轴；w为索z方向运动分量；H为索静拉力弦向分量；h索运动引起的附加拉力弦向分量；E为材料弹性模量；I为截面惯性矩；m为单位长度质量。

对于材料及截面性质为常量的均匀水平索而言，式(1)实际上与文献[9]中的考虑弯曲刚度的弦的运动方程相同，不同之处仅在于具体计算时考虑了拉索垂度的影响。对于斜索而言，由于其未考虑弦向力的变化效应，也看作是文献[7]中理论计入弯曲刚度后的结果，关于不考虑弯曲刚度斜索的更准确的理论可见文献[10-11]。

图1斜索计算图示

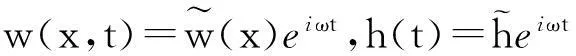
(2)

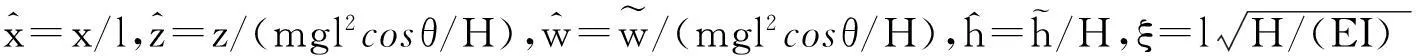
在图1所示坐标系下，斜索的静力构形可通过对文献[12]的近似表达进行坐标变换得到：

(3)

其中，ε=mglsinθ/H为Irvine引入的小参数，用于摄动法求解。

对于拉索来说，由于以承受轴力为主，这里仅考虑了轴力应变而忽略了弯曲应变。由此可得到索方程为[12]：

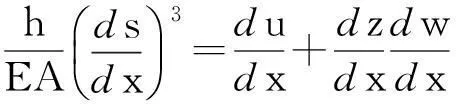
(4)

其中：u为索纵向运动分量；s为弧长坐标；EA为索抗拉刚度，利用两端的边界条件并对其进行无量纲化后可得：

(5)

其中，λ2=(mglcosθ/H)2l/(HLe/EA)为Irvine[12]引入的参数，其反映了索弹性效应和几何效应的影响，Le为索有效长度，其表达式为

这里可近似取为Le≈l[1+(mglcosθ/H)2/8][12]。

1.1两端铰接[6]

(6)

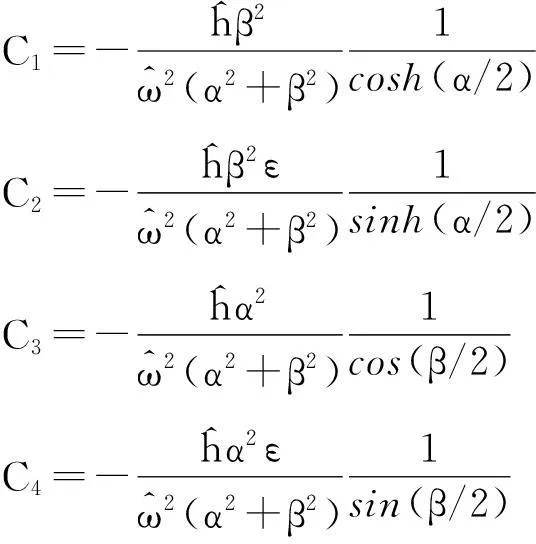
(7)

将其代入通解中即得振型函数：

(8)

再利用索方程(5)可得无量纲形式频率方程为：

(9)

式(8)和式(9)是在本文的无量纲参数表示和坐标系下考虑弯曲刚度的两端铰接斜索的面内固有振动的振型函数和频率方程，其实际上与文献[6]的结果是一致的。当ε=0时，式(9)就退化相应的水平索对称振型频率表达。

1.2两端固接

(10)

(11)

当ε=0时，振型函数和式(11)就退化为文献[2]的水平索表达。

2讨论

由此可见，考虑弯曲刚度的影响在某些情况下是必要的；而对于需要考虑弯曲刚度的斜索振动分析，考虑不同边界条件的影响也是必要的。

对于斜拉索而言，两端固接和两端铰接可以看作实际的约束条件的上下界，它们是实际约束的理想状态。文献[5]就曾指出，实际的约束条件通常既非固接亦非铰接，而是处于某个中间的状态。这样，在实际应用中，当需要精确考虑拉索的边界约束条件时，可以采用式(9)和式(11)对其进行估计和近似。

图3表示ξ=75，ε取0.05、0.0966、0.1366、0.1673(由于参数ε是索构型近似表达的摄动参数，所以从理论上讲，其应该为小值)，在假设其它无量纲参数不变时，其分别可以看作θ取15°、30°、45°、60°的情况(即假设参数mgl/H保持不变)。由图3可见，ε的变化对频率的影响很小(由于差别很小，图中未标出各曲线的意义)，但基本上是随着ε的增大，相应的两阶频率在曲线的上升段越接近。ξ取其它值时基本上也有类似的结论。

图4给出了ε=0.1，ξ=75，λ分别取1.372π和3.330π[11]两种情况下，两种边界条件下的振型图。从图中可见，斜索振型为非对称的[6-7,11,14]，实际上，由于斜索本身无对称轴可言，这一点从定性角度可以直接判断；相比于两端铰接条件，两端固接条件下的振型的非对称性较弱，这一点对于高阶振型更加明显。由此可见，不同的边界条件对振型的影响还是比较大的(如图4(a)中的第二阶和图4(b)中的第一阶)，这就再次体现了考虑不同边界条件的必要性。关于ε和ξ取其它值时，基本可得到类似的结论。

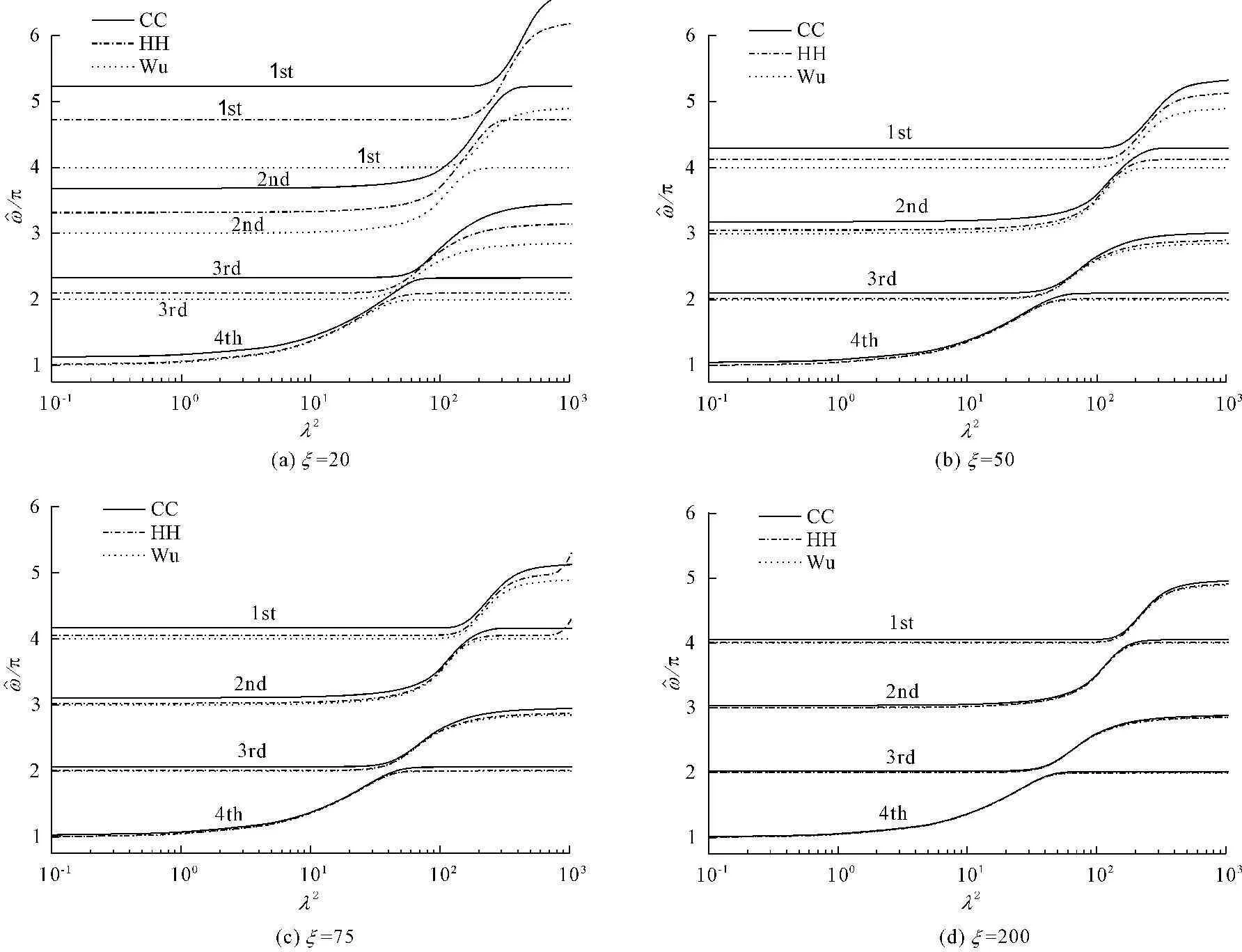
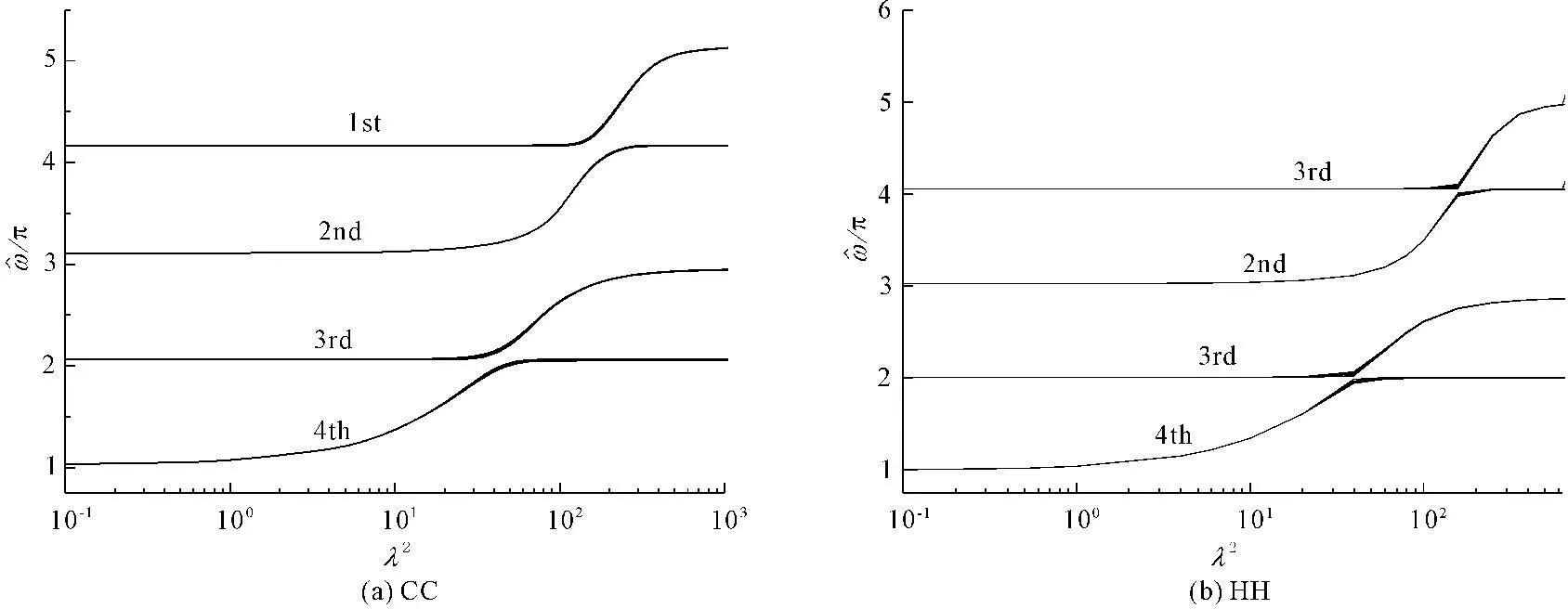
图2　两种边界条件下前四阶频率对比图

图3两种边界条件下不同ε值时前四阶频率对比图

3结论

在已有两端铰接解析解的基础上，在中点割线坐标系Oxz下，补充了两端固接边界条件下考虑弯曲刚度的斜索面内自由振动解析解。分析结果表明：斜索无Crossover现象，其振型不具对称性，考虑弯曲刚度的频率要大于不考虑弯曲刚度的频率，两端固接频率大于两端铰接频率。通过讨论可知，考虑弯曲刚度在某些情况下是必要的；对于需要计入弯曲刚度的斜索而言，应该考虑不同边界条件对自由振动的影响；两端固接和两端铰接可以看作是实际拉索约束情况的上下界，可采用本文公式对斜索的自振频率进行估计和近似。

参考文献：

[1]Ni Y Q, Ko J M, Zheng G. Dynamic analysis of large-diameter sagged cables taking into account flexural rigidity[J]. Journal of Sound and Vibration, 2002,257(2):301-319.

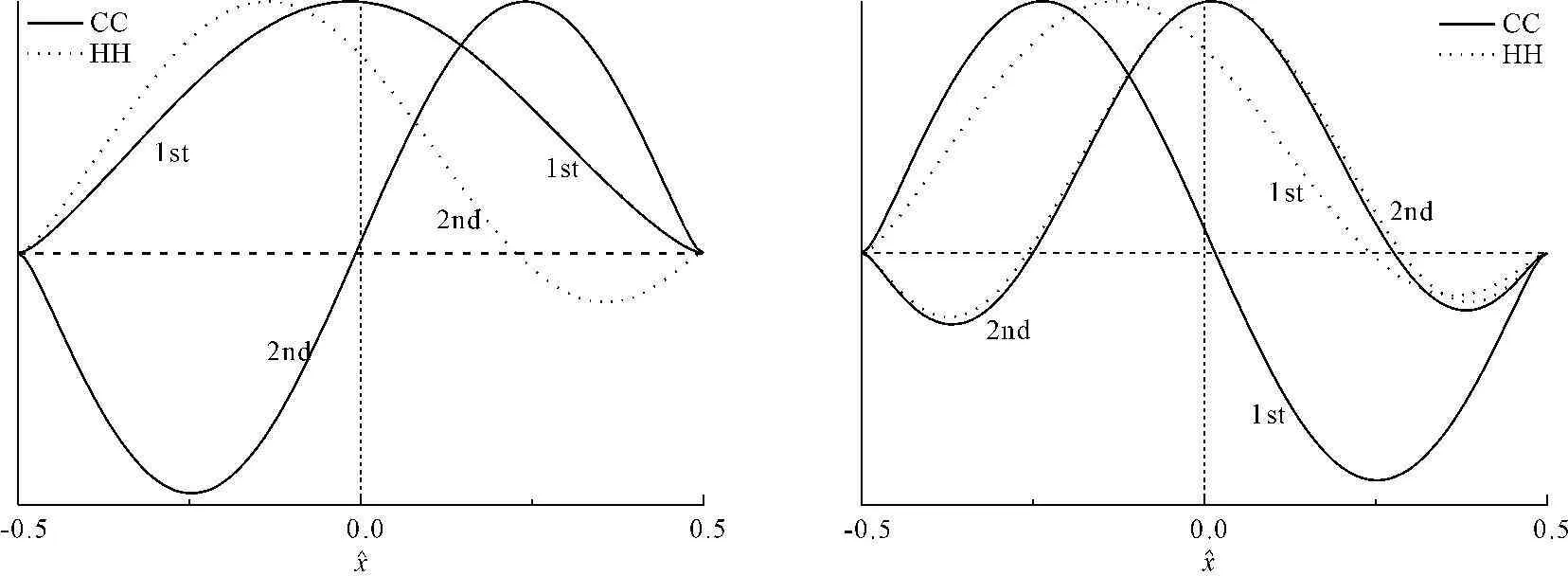
图4前两阶振型图

[2]Ricciardi G, Saitta F. A continuous vibration analysis model for cables with sag and bending stiffness[J]. Engineering Structures, 2008,30(5):1459-1472.

[3]Zui H, Shinke T, Namita Y H. Practical formulas for estimation of cable tension by vibration method[J]. Doboku Gakkai Ronbunshu, 1996,122(6):651-656.

[4]Ren W X, Chen G, Hu W H, et al. Empirical formulas to estimate cable tension by cable fundamental frequency[J]. Structural Engineering and Mechanics, 2005,20(3):363-380.

[5]Kim G H, Park T. Estimation of cable tension force using the frequency-based system identification method[J]. Journal of Sound and Vibration, 2007,304(3/5):660-676.

[6]吴庆雄，李浏，陈宝春.考虑弯曲刚度的拉索面内固有振动的理论计算公式[J].工程力学，2010,27(11):9-15.

[7]吴庆雄，陈宝春.塔桅结构的斜索面内固有振动计算的修正Irvine方程[J].工程力学,2007,24(4):18-23.

[8]严国敏.现代斜拉桥[M].成都:西南交通大学出版社,1996:49-64.

[9]Mehrabi A B, Tabatabai H. Unified finite difference formulation for free vibration of cables[J]. Journal of Structural Engineering, 2014,124(11):1313-1322.

[10]Kim J, Chang S P. Dynamic stiffness matrix of an inclined cable[J]. Engineering Structures, 2001,23(12):1614-1621.

[11]Zhou X D, Yan S Z, Chu F L. In-plane free vibrations of an inclined taut cable[J]. Journal of Vibration and Acoustics, 2011,133(3):470-476.

[12]Irvine H M. Free vibration of inclined cables[J]. Journal of Structural Division, ASCE, 1978,104(2):343-347.

[13]李庆阳,易大义,王能超.现代数值分析[M].北京:高等教育出版社,1995:252-285.

[14]Triantafyllou M S. The dynamics of taut inclined cables[J]. Quarterly Journal of Mechanics and Applied Mathematics, 1984,37(3):421-440.

Note on In-plane Free Vibration Solution of Inclined Cables >Considering Bending Stiffness

XIAO Yi1,2

(1.CollegeofCivilEngineering,FujianUniversityofTechnology,Fuzhou,Fujian350118,China;2.FujianProvincialKeyLaboratoryofAdvancedTechnologyandInformatizationinCivilEngineering,Fuzhou,Fujian350118,China)

Abstract：Accurate modeling of cables needs to consider the bending stiffness. At present for the free vibration of inclined cables considering bending stiffness, only the analytical solution of hinged boundary conditions has been obtained which is not the case in real world problems. Based on the existing research, the solutions of in-plane free vibration of inclined cables considering bending stiffness were derived in secant coordinate system with the origin in the midpoint of the chord length, the analytical solution of clamped conditions was deduced for supplement. The analysis show that the crossover phenomenon does not exist for inclined cables, and the mode shape is asymmetric. The frequencies with bending stiffness are larger than the one without it. The frequencies of clamped conditions are larger than the hinged ones. The comparison demonstrates that bending stiffness should be considered in some situations. Different boundary conditions should be considered in the analysis. Due to the upper and lower bound properties of ideal boundaries, the present results can be used as an estimation and approximation of real situations.

Keywords:inclined cable; free vibration; bending stiffness; analytical solution

文章编号：1672—1144(2016)01—0155—05

中图分类号：U441+.3

文献标识码：A

作者简介：肖一(1982—)，男，辽宁盘锦人，讲师，工程师，主要从事索结构问题方面的工作。E-mail: xiaoyiArchive@fjut.edu.cn

基金项目：福建工程学院科研启动基金(GY-Z14013)

收稿日期：2015-07-15修稿日期：2015-09-04

DOI:10.3969/j.issn.1672-1144.2016.01.029