基于博弈论改进TOPSIS模型的构建及应用

袁　伟，王　毅，文　俊

(重庆市水利电力建筑勘测设计研究院， 重庆 400020)



基于博弈论改进TOPSIS模型的构建及应用

袁伟，王毅，文俊

(重庆市水利电力建筑勘测设计研究院， 重庆 400020)

摘要：对工程方案进行综合比选时，传统方法往往因指标定权计算方法选用不适宜，进而影响到评价结果的精度和合理性。综合考虑生态效益、经济效益、社会效益，按照实用性、代表性等原则建立评价指标体系，提出用“垂直距离”替代“欧式距离”对传统的TOPSIS模型进行改进，从而建立基于博弈论的改进TOPSIS模型，并将该模型用于重庆市境内的双溪河整治工程的方案优选中。实例应用结果表明，该方法用于工程方案的综合评价是可行的，评价结果较为可靠、合理，为其他工程方案综合评价提供了一种新方法和借鉴经验。

关键词：逼近理想解的排序法；集对分析；博弈论权重；最小相对熵原理

在河道整治、地基处理等工程中，工程投资、施工难度和工期等将会成为选择工程方案的制约因素，通常要对多个工程方案进行综合比选，然而多个待选方案的综合评价问题属于多层次、多属性和多目标的决策问题，由于受到多种制约因素的影响，使得决策问题具有一定的不确定性。SPA为一种处理随机性、模糊性和不确定性的系统方法，得到了广泛的应用[1-5]，文献[2-5]将集对分析理论运用于不同领域，解决相关的实际问题，均得出相对合理的研究成果，但往往忽视了对评价指标权重计算方法作深入研究和分析，不同权重计算方法对评价结果的影响程度以及探求更为合理的组合权重计算方法值得进一步研究。在文献[6]中将集对分析(SPA)和TOPSIS两种理论进行耦合，利用集对分析的同一度矩阵构建规范决策矩阵，建立了改进的TOPSIS模型，提高了其鉴别优劣排序的能力。本文对文献[6]提出改进的TOPSIS模型作进一步改进，提出用“垂直距离”替代“欧式距离”，并将该改进TOPSIS模型用于河道整治工程方案比选中，解决多方案优劣排序问题。本文采用“博弈论”法[7]求解组合权重，该法具有适用范围广、计算简便和概念清晰等优点。

1模型建立

1.1TOPSIS和SPA理论

TOPSIS[8]方法具有计算简便、概念清晰的特点，主要用于解决多目标、多属性决策问题，这与河道整治综合评价决策问题相适宜，其具体思路详见文献[9]。但传统TOPSIS模型存在一个较为明显的不足之处，可能同时出现与理想解和负理想解的欧式距离均接近的情况，再利用相对欧式距离作方案优劣排序，存在一定的不足。为解决这个问题，提出用“垂直距离”来替代欧式距离。文献[9]给出“垂直距离”的定义即在理想解和负理想解之间存在两点，过这两点作理想解和负理想解连线为法向量的平面之间的距离。如果一个方案与理想解的“垂直距离”较近，那么与负理想解的“垂直距离”就远，证明过程详见文献[9]。

SPA[1]在给定的问题背景下，对所论的集对进行同、异、反的定量分析，联系度计算公式如下：

u=a+bi+cj

(1)

式中：a、b和c分别为同一度、差异度和对立度，且满足a+b+c=1；i在[-1，1]中取值，j为对立度系数，一般恒取-1。

若所论的集对只须进行同一性、同一度进行分析，对其差异性、对立性不作分析，同一性、同一度的概念定义参见文献[6]。集对同一度的计算规则参见文献[10]。

1.2基于博弈论组合权重的改进TOPSIS模型

步骤1：建立待评方案集、评价指标集

假设有m个待评方案和有n个评价指标，以此建立待评方案集A={A1，A2…Am}和评价指标集P={P1，P2…Pn}，每个指标值均为非负有理数。对于成本型指标越小越优，比如工程投资、工程占地面积等；对于效益型指标越大越优，比如安全性、可靠性等。

步骤2：确定理想方案A0

对于某一个评价指标，理想方案A0的取值：即从m个待评价方案中选择最优值：

A0={P01，P02…P0n}

(2)

步骤3：同一度矩阵R

根据文献[10]，同一度矩阵R=(rik)m×n，其中的元素rik为：

当PikP0k，则有rik=P0k/Pik

(3)

步骤4：规范决策矩阵Z

根据同一度矩阵R构建规范决策矩阵Z=(zik)m×n，其中的元素zik为[11]：

(4)

步骤5：计算各指标的组合权重wkc

对于评价指标的权重计算，若仅考虑主观赋权法，往往因客观信息考虑较少带来一定的误差，影响到评价结果的精度；相应地若仅考虑客观赋权法，指标赋权有了客观依据，可以充分挖掘数据的客观属性，但专家的经验对指标赋权具有不可忽视的作用。为充分发挥两种赋权法的优势，主观赋权采用专家打分法确定，客观权重采用熵权法确定，熵权法计算公式参见文献[12]，用博弈论求解各指标的组合权重，称其为“博弈论”法，具体计算公式如下[7]：

假设有L种方法计算指标权重，得到指标的权重向量：

wj=(wj1，wj2…wjn)，(j=1,2,…,L)

(5)

对于组合权重w，则L种权重向量的线性组合：

(6)

为了使组合权重w与每一个权重wj的离差极小化，由此可建立对策模型：

(7)

根据矩阵的微分性质，可以推导出上式的最优化的一阶导数条件：

(8)

由上式可以计算求得(α1，α2，…αL)，对其进行归一化处理，可得组合权重wc：

(9)

为了对不同组合权重计算方法进行比较，仅介绍两种常用的计算方法如下：

(1) 文献[13]运用最小相对熵原理求解组合权重，称其为“最小相对熵原理”法，构造的目标函数和约束条件为：

(10)

(11)

(12)

(2) 文献[14]运用优化决策模型求解组合权重，称其为“优化决策模型”法，构造的目标函数和约束条件为：

(13)

(14)

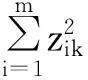
(15)

若仅2组权重向量计算组合权重，“优化决策模型”法是“博弈论”法的简化形式，即wc=α1·w1k+α2·w2k,(α1+α2=1)，由此可见，“博弈论”法适用于L≥2的情况，而“优化决策模型”法仅适用于L=2的情况。

步骤6：建立加权规范决策矩阵X=(xik)m×n，其中的xik：

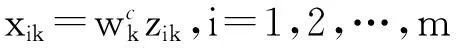
(16)

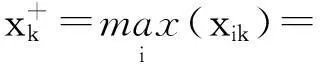
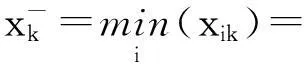
(17)

根据文献[9]，平移矩阵T=(tik)m×n，其中的tik：

(18)

步骤8：计算“垂直距离”Di

计算各方案与理想解的“垂直距离”Di，其计算公式为：

(19)

Di值表明方案接近理想解的程度[15]，Di值越小，说明距离理想解越近，则待评价方案越优。

2模型应用

选用重庆市境内的双溪河(为御临河的二级支流)的河道整治工程的相关资料来验证本文所建立模型的可行性和合理性，该河流于2013年进行河道整治时提出3种治理方案：

方案1：“抬高式”明渠方案；

方案2：“箱涵+非常溢洪道”方案；

方案3：明渠方案。

评价指标根据河流实际情况选定，共选择7个评价指标：工程投资X1，万元/m；工程占地面积X2，亩；工程景观性X3；工程安全性X4；工程亲水性X5；工程施工强度因子X6；工程施工导流难度X7。三种治理方案的具体数据见表1。

表1　三种治理方案特性表

由表1可知，理想方案A0={2.17，124.73，0.8，0.8，0.7，0.3，0.4}，由公式(3)和公式(4)可得同一度矩阵R和规范决策矩阵Z，根据文献[12]给出的熵权法计算步骤可得各指标的客观权重w(o)={0.1429，0.1412，0.1431，0.1339，0.1597，0.1488，0.1303}，各指标的主观权重通过专家咨询打分，得到各指标的主观权重w(s)={0.1653，0.1488，0.1405，0.1570，0.1405，0.1322，0.1157}，由式(7)～式(9)、式(12)(α1=0.761，α2=0.239)和式(15)(μ取0.5)得到各指标的组合权重见表2，再将表2中组合权重计算结果分别代入式(16)～式(19)可得评价结果见表3。

由表2可知，采用不同组合权重法计算得到的指标组合权重值差别不大，各指标在指标集中的重要程度没有受到影响；式(15)是式(9)的最简化形式(L=2)，两者计算结果应相同，两者计算结果不同是由于主观和客观权重的比重系数不同造成的，假如μ取0.761，则两种组合权重的计算结果则完全相同。不难发现，“博弈论”法中比重系数的确定是严格按照公式计算出来的，不存在主观因素，其组合权重计算结果相对较合理、可靠，而“优化决策模型”法中的偏好系数 的确定则由主观偏好决定，存在较大的不确定性和随意性。

表2　各指标的组合权重对比表

表3　不同评价方法求得的评价结果对比表

由表3可知，三个治理方案的优劣顺序：方案1>方案2>方案3，即方案1是最优方案，本文的评价结果与该河道治理采用的最终方案(“抬高式”明渠方案)一致。为了进一步验证本文评价结果的正确性，利用文献[10]构建的评价模型，各指标权重采用公式(9)计算得到的组合权重，其计算结果见表3。由文献[10]构建的评价模型计算得到的排列顺序：方案1>方案2>方案3，与本文的评价结果一致，从而进一步验证了改进的TOPSIS模型可行性和正确性。

3结语

(1) 运用集对分析处理决策问题中的不确定性信息，利用同一度矩阵构建规范决策矩阵，是传统TOPSIS模型的一次改进；利用“垂直距离”替代欧式距离，对文献[6]的TOPSIS模型作进一步改进，进而提高模型评判方案的优劣能力，采用熵权法计算各指标的客观权重，采用专家打分法得到各指标的主观权重，运用“博弈论”法结合主观、客观权重求得组合权重。

(2) 采用不同组合权重法计算得到的指标组合权重值差别不大，各指标在指标集中的重要程度没有受到影响，同时本文提出的“博弈论”法求解组合权重，计算结果相对较合理、可靠。“优化决策模型”法仅适用于2种方法计算指标权重的情形，而“博弈论”法适用于2种及以上方法计算指标权重的情形，因此该法具有适用范围广、计算简便和概念清晰等优点。

(3) 河道整治工程方案综合评价属于多层次、多属性和多目标的决策问题，本文提出的评价模型为解决多层次、多属性和多目标的决策问题提供了一个新途径，具有一定的应用价值。

参考文献：

[1]赵克勤.集对分析及初步应用[M].杭州:浙江科学技术出版社,2000.

[2]李文君,邱林,陈晓楠,等.基于集对分析与可变模糊集的河流生态健康评价模型[J].水利学报,2011,42(7):775-782.

[3]汪明武,赵奎元,张立彪.基于联系期望的膨胀土和改良土胀缩性评价模型[J].岩土工程学报,2014,36(8):1553-1557.

[4]汪明武，陈光怡，金菊良.基于多元联系数-三角模糊数随机模拟的围岩稳定性风险评价[J].岩土工程学报, 2011,33(4):643-647.

[6]袁伟.改进的TOPSIS模型在基坑支护中的应用[J].长江科学院院报,2014,31(8):82-86.

[7]刘国颂,綦春明,聂春龙,等.基于博弈论组合赋权边坡稳定性集对分析[J].长江科学院院报,2014,31(6):83-88.

[9]张振东，潘妮，梁川.基于改进TOPSIS的长江黄河源区生态脆弱性评价[J].人民长江,2009,40(16):81-84.

[10]冯玉国,王渭明.基于集对分析同一度的基坑支护方案综合评价[J].岩土工程学报,2008,30(9):1389-1392.

[11]王丽萍,郑江涛,周晓蔚,等.山区河流可持续发展能力评价研究[J].水利学报,2012,43(6):726-733.

[12]袁伟,彭建.基于熵权的河流水质评价模糊集对分析模型[J].水利科技与经济,2011,17(1):12-14.

[13]邱苑华.管理决策与应用熵学[M].北京:机械工业出版社,2002.

[14]陶菊春,吴建民.综合加权评分法的综合权重确定初探[J].系统工程理论与实践,2001(8):43-48.

[15]张先起,梁川,刘慧卿,等.改进的TOPSIS模型及其在黄河置换水量分配中的应用[J].四川大学学报:工程科学版,2006,38(1):30-33.

Establishment and Application of the Improved TOPSIS Model Based on Game Theory

YUAN Wei, WANG Yi, WEN Jun

(ChongqingSurveyingandDesignInstituteofWaterResources,ElectricPowerandArchitecture,Chongqing400020,China)

Abstract：The conventional method is not suitable for comprehensive evaluation of project schemes due to its improper selection of calculation method for index weights, and then, the inappropriate method will affect the accuracy and rationality of the evaluation results.With comprehensive consideration of maximizing ecological benefit, economic benefit and social benefit, an evaluation index system was established according to the practical and representative principle. The conventional TOPSIS model was improved by replacing “Euclidean distance” with “vertical distance”, and a new model based on game theory was established and applied to the evaluation of Shuangxi river regulation schemes in Chongqing. The application result indicates that, this method is suitable for the comprehensive evaluation of project schemes with reliable and reasonable results. This new method provides a new approach and some reference for the evaluation of other project schemes.

Keywords:TOPSIS; SPA; game theory weights; minimum relative entropy principle

文章编号：1672—1144(2016)01—0188—04

中图分类号：TV85

文献标识码：A

作者简介：袁伟(1985—)，男，安徽定远人，硕士，工程师，主要从事水工结构及基础处理方案优选等方面的研究工作。

收稿日期：2015-07-30修稿日期：2015-08-27

DOI:10.3969/j.issn.1672-1144.2016.01.035

E-mail：abc123-126@163.com