基于动力特性的螺栓连接钢框架结构有限元建模

汪志昊， 陈银， 郜辉， 李国豪， 郜家奇

(华北水利水电大学 土木与交通学院,河南 郑州450045)

基于动力特性的螺栓连接钢框架结构有限元建模

汪志昊， 陈银， 郜辉， 李国豪， 郜家奇

(华北水利水电大学 土木与交通学院,河南 郑州450045)

合理选取螺栓节点处理方式与确定层间柱有效长度，是螺栓连接钢框架结构有限元建模的难点所在。首先对3层螺栓连接钢框架结构室内模型进行了动力特性测试，然后采用ANSYS分析软件开展了结构三自由度集中参数有限元模型和板-梁有限元模型的动力特性分析。板-梁有限元模型的螺栓节点分别按铰接、半刚性连接、刚接处理。通过对比结构前3阶模态的自振频率、振型的有限元值与实测值发现：螺栓节点按半刚性处理较为合理。为了进一步提高半刚性节点处理板-梁有限元模型的精度，将模型的实测动力特性值代入三自由度集中参数模型，反推结构层间柱的实际有效长度，并对有限元模型进行修正。研究表明：在结构层间柱的实际有效长度修正后，结构动力特性的计算精度可以得到进一步提升。

钢框架结构；螺栓连接；有限元模型；动力特性测试；模型修正

螺栓连接作为钢结构的重要连接方式，具有构造简单、拆装方便、调整容易等特点。然而，螺栓连接节点存在摩擦、接触、拧紧程度等问题，属于典型的非线性、不确定性问题，为螺栓连接钢框架结构的有限元建模带来了困难。张根辈等[1]采用刚性约束单元RBE2模拟螺栓连接，并应用于实体和板-梁有限元建模中。魏群等[2]采用螺栓精细化处理和铰接简化处理两种方式对螺栓焊缝连接梁柱结构进行有限元建模，并对比分析了两个模型的静力特性。研究表明：建立螺栓连接钢结构有限元模型时，采用文献[1-2]的方法对螺栓连接进行精细化建模虽然精度较高，但建模较为复杂，且计算量显著增大，若简化为刚接或铰接又存在较大误差。因此，合理处理螺栓节点的连接方式，使其在静动力有限元分析时尽可能真实地反映结构的力学行为，是影响有限元建模可信度的重要问题。

此外，结构有限元模型与实际结构之间不可避免地存在着误差，有限元模型修正技术是有限元精细化建模的重要手段。结构有限元模型修正一般是基于结构静动载试验结果来修正、更新有限元模型的刚度、质量、几何尺寸等参数的取值[3]。如黄志强等[4]采用联合运用静动力目标函数的方法对一海洋井架有限元模型进行材料弹性模量、密度及构件尺寸等参数的修正，达到了很好的模型修正效果。秦玉灵等[5]采用自适应二次粒子群算法对某5层钢架结构模型的质量、弯曲刚度等参数进行了修正。刘继承等[6]提出了一阶搜索优化有限元模型修正算法。黄民水[7]通过ANSYS参数化设计语言(APDL)形成优化文件来修正有限元模型的相关参数。

本文结合某螺栓连接钢框架结构室内模型的动力特性实测结果，分别从螺栓节点优化处理、层间柱实际有效长度修正两个方面对该结构的有限元精细化建模开展研究。

1 结构模型概况

螺栓连接3层钢框架结构模型由立柱、梁、楼板和底座构成，层高0.3 m，模型结构如图1所示。模型的材料及规格尺寸见表1。钢材采用Q235钢，弹性模量为2.06×105MPa,泊松比为0.3，密度为7.85×103kg/m3。

结构模型梁柱接触节点均采用单颗M10螺栓连接；楼板通过螺栓固定在梁上；在每个柱脚部位，柱由两块角钢夹持并点焊后固定于底座钢板上；模型底座钢板固定于刚性地面。

图1 钢框架结构模型示意图

名称 类型规格长度/mm数量/(根/块)立柱扁钢30mm×3mm9004梁等边角钢L30mm×5mm4966梁等边角钢L30mm×5mm3966楼板钢板500mm×400mm×4mm—3底座钢板600mm×600mm×10mm—1柱脚等边角钢L50mm×4mm608

2 结构动力特性测试

2.1 测试仪器及方法

测试设备和仪器主要有：DH5935N型动态数据采集系统、891-4型拾振器。试验采用人工激振测试3层钢框架结构的前3阶模态自振频率与振型。为保证激振效果，分别在第1、2、3层处进行各阶模态的人工激振。测试信号采样频率为200 Hz，信号频谱分析时分析点数均取为1 024点。

2.2 试验及数据处理

基于功率谱密度的峰值法(PP法)对振动信号的实测数据进行分析。综合时间波形和自功率谱，分析结构模型振动的前3阶模态自振频率和振型。图2、图3分别给出了人工激振下结构第1阶模态第3层测点和第2阶模态第1层测点的自由衰减振动的时间历程曲线。

图2 第1阶模态第3层测点自由振动的时间历程曲线

图3 第2阶模态第1层测点自由振动的时间历程曲线

由图2与图3可以看出：人工激振作用下，结构的振动波形明显，信号的信噪比较高。

振型描述了结构体系自身振动的形态，是结构自振特性的重要参数之一。对结构的实测振型进行质量归一化处理：

(1)

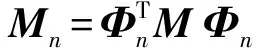
(2)

(3)

由第1、2、3阶波形自功率谱识别得到结构前3阶自振频率与质量归一化振型如图4所示。

图4 模态测试识别得到的结构前3阶振型和频率

3 有限元建模分析

采用有限元分析软件ANSYS，对3层钢框架模型建立质量-梁三自由度集中参数有限元模型和板-梁有限元模型，并进行模态分析。

3.1 有限元建模

根据图5所示的质量-梁三自由度集中参数模型示意图建立三自由度集中参数有限元模型。结构每层梁和板的总质量等效为集中质量，层间柱刚度等效为集中刚度，考虑结构x方向前3阶的弯曲模态。有限元模型采用BEAM4单元模拟立柱，采用MASS21单元模拟集中质量；约束在柱脚位置节点的全部自由度。考虑梁柱接触连接的复杂性，规定层间柱初始长度均为螺栓间净距，即li为0.29 m。集中质量m均取为11.01 kg，柱截面惯性矩均取为6.75×10-11m4。

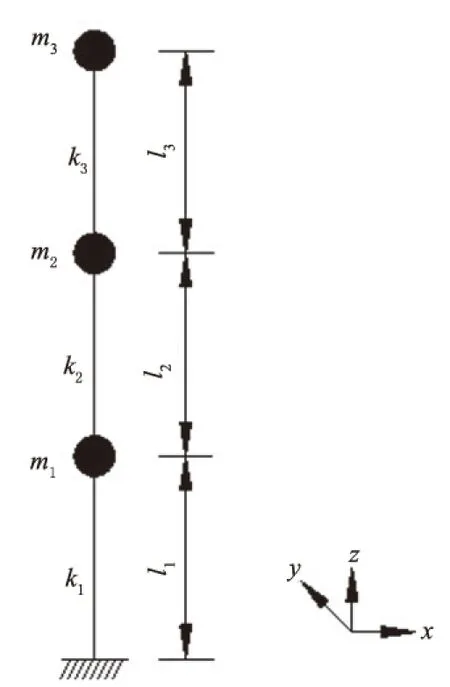
图5 质量-梁三自由度集中参数模型示意图

结构板-梁有限元模型如图6所示。分别采用BEAM4、BEAM3与SHELL63单元模拟立柱、梁与楼板，建立柱、梁与板模型；在柱脚位置施加固端约束。

由于螺栓拧紧程度等原因，梁柱接触位置的螺栓连接对结构平面内自振特性的影响主要取决于梁柱的连接刚度。考虑到绕柱弱轴转动自由度ROTY对结构振动的显著影响，建立结构板-梁有限元模型时，应用位重合节点耦合命令(cpintf)，通过改变耦合时ROTY的约束情况来实现不同刚度的螺栓连接形式。当所有梁柱螺栓节点在耦合时都无该约束，即为节点铰接；当所有梁柱螺栓节点在耦合时都有该约束，即为节点刚接；当模型一端的梁柱螺栓节点在耦合时有约束，另一端无约束，则等效为节点半刚性连接。根据各节点ROTY自由度约束情况的不同处理方式，分别建立了铰接、半刚性连接与刚性连接的板-梁有限元模型，拟通过对比3种有限元模型的结果，获得与实际螺栓连接相符度较高的螺栓简化处理方式。

图6 板-梁有限元模型

3.2 有限元计算结果及分析

应用ANSYS软件对钢框架结构的不同有限元模型进行模态分析，据此得到结构前3阶模态的自振频率。自振频率有限元值与实测值对比见表2。

表2 结构自振频率有限元值与实测值对比

由表2可知：不同有限元模型计算得到的结构固有频率存在明显差异；对于板-梁结构模型，随着梁柱节点连接刚度的增加，模型固有频率显著提高；集中参数模型与螺栓连接半刚性简化处理的板-梁模型所得固有频率与结构实测固有频率较为接近。鉴于结构高阶模态频率测试值与有限元计算值均可能存在较大误差，本文重点对比分析结构第1、2阶模态的固有频率。研究表明：节点半刚性处理的板-梁有限元模型结构第1、2阶固有频率的误差均在10%范围内，而简化为刚接或铰接处理的板-梁有限元模型的误差均超出30%，即铰接或刚接处理螺栓连接都出现了模拟显著失真现象。因此，将螺栓节点连接刚度处理为半刚性连接更符合结构的实际情况。

然而，由半刚性连接处理有限元模型所得结构的固有频率与实测值对比可知，结果仍存在一定偏差。因此，有必要对有限元模型其他不确定因素进行进一步修正。

4 有限元模型修正

该3层钢框架模型有限元建模时，各层的质量、刚度等参数取值较为明确，主要的不确定性参数为层间柱的长度取值。因此，有必要对结构各层间柱的长度进行修正。

将3层钢框架结构简化为三自由度集中参数模型是结构动力学领域的常见处理形式。在三自由度模型中，层间抗侧刚度构成结构刚度矩阵。各层间结构的抗侧刚度为：

(4)

式中：I为柱截面绕弱轴的惯性矩；li为各层间柱的长度；b为柱截面宽度；h为柱截面厚度。

由式(4)可知，抗侧刚度k与柱层间长度li的3次方成反比。因此，当层间柱长度li变化时，对结构刚度的影响较明显。为得到精细化的有限元模型，现对模型柱层间长度li进行修正。

4.1 修正有限元模型

根据结构三自由度集中参数模型，可由结构的实测频率和振型值反推出各层柱的抗侧刚度，再通过柱的抗侧刚度反算层间柱的实际有效长度[1]。根据结构动力特性测试所得的自振频率和振型重建集中参数模型。模型的质量和刚度矩阵分别为：

M=(Φ-1)TΦ-1，

(5)

(6)

(7)

对比式(6)和式(7)，考虑测试频率和振型误差，并结合ANSYS验算，可反推第1、2、3层柱的实际有效长度分别约为：0.337、0.275、0.263 m。可见：层间柱的总实际有效长度略小于柱初始总长度；因柱脚通过角钢固定，再加上传感器的安放，致使首层柱的实际有效长度大于初始值；由于梁柱接触连接，第2、3层柱的实际有效长度略小于初始值。将各柱的实际有效长度代入有限元模型中，即可得到修正后的三自由度集中参数有限元模型和板-梁有限元模型。

4.2 对比与分析

对修正后的有限元模型进行模态分析，得出结构的固有频率及误差见表3。

表3 有限元模型修正后的自振频率及误差

对比表2和表3可知，修正后有限元模型的固有频率计算值与实测值之间的误差均减小。通过修正层间柱的长度，有效提高了有限元建模的精度。

考察振型的相关性可以检验模型修正的准确性。有限元计算振型和实测振型的相关性可以通过模态保证准则来计算。模态保证准则(Modal Assurance Criterion，MAC)为[3]：

(8)

式中：Φs为模态试验实测质量归一化振型；Φi(i=1,2,3)为质量归一化振型。

MAC介于0和1之间。如果模态完全相关，则MAC=1；如果模态完全不相关，则MAC=0。

研究有限元模型修正前后所得振型与实测振型之间的相关性，得出各振型模态保证准则见表4。由表4可知：有限元模型修正后，结构前3阶模态振型的相关性均有所提高；板-梁有限元模型的MAC接近于1，相关性较好；集中参数有限元模型第1阶模态振型的相关性较好，而第2、3阶模态振型的相关性较差。

表4 有限元模型修正前后振型MAC对比表 %

5 结语

1)基于动力特性的螺栓连接钢框架结构有限元建模，螺栓节点宜处理为半刚性连接。

2)螺栓连接钢框架结构的层间柱长度取值对结构动力特性有限元值的影响较大，是该类结构有限元精细化建模的难点。

3)将螺栓连接钢框架结构简化为集中参数有限元模型后，结构固有频率的误差相对较小，但结构振型的相关性偏差。

4)螺栓连接钢框架结构有限元精细化建模的影响因素众多，有必要进一步深入研究。

[1]张根辈,臧朝平,王晓伟,等.螺栓连接框架结构的有限元模型修正[J].工程力学,2014,31(4):26-33.

[2]魏群,姜华.钢结构有限元计算的精细模型建立[J].华北水利水电学院学报,2013,34(3):9-12，129.

[3]宗周红,任伟新.桥梁有限元模型修正与模型确认[M].北京:人民交通出版社,2012:3-6，16.

[4]黄志强,张坤,邱成松,等.基于静动力分析的海洋井架钢结构有限元模型修正方法[J].应用力学学报,2015,32(4):611-617，705-706.

[5]秦玉灵,孔宪仁,罗文波.自适应二次粒子群算法钢架模型修正[J].计算机科学,2010,37(9):249-251.

[6]刘继承,周传荣.一个基于优化的有限元模型修正方法[J].振动与冲击,2003,22(2):35-36，101.

[7]黄民水.基于优化理论的某钢框架模型修正研究[J].钢结构,2009,24(5):21-23，50.

[8]刘晶波,杜修力.结构动力学[M].北京:机械工业出版社,2012:107-108.

(责任编辑：陈海涛)

Finite Element Modeling of Bolted Steel Frame Structure Based on Dynamic Characteristics WANG Zhihao, CHEN Yin, GAO Hui, LI Guohao, GAO Jiaqi

(School of Civil Engineering and Communication, North China University of Water Resources and

Electric Power, Zhengzhou 450045, China)

The finite element modeling of bolt connection steel frame structure has the difficulties such as reasonable selection of bolt joint treatment and determination of effective length of interlayer column. Firstly, the dynamic characteristics of a three-layer bolted steel frame structural model are tested. Then, the dynamic characteristics of the finite element model of structural three-degree-of-freedom concentrated parameter and the plate-beam finite element model are analyzed by ANSYS software. The bolt nodes of the plate-beam finite element model are treated as the hinge, the semi-rigid connection, the rigid connection, respectively. By contrasting the first 3 order natural frequencies and vibration modes between the finite element values and the tested values, it is found that the semi-rigid treatment of the bolted joints is reasonable. In order to further improve the accuracy of the finite element model of the plate-beam interaction with the semi-rigid joints, the measured dynamic characteristic values of the model are substituted into the three-degree-of-freedom concentration model, and then, the effective length of the inter-column is calculated and the finite element model is modified. The results show that the calculation accuracy of structural dynamic characteristics can be further improved after the practical effective length of structural columns is corrected.

steel framed structure; bolted connection; finite element model; dynamic characteristics test; model updating

2016-09-25

国家自然科学基金资助项目(51308214);河南省高等学校青年骨干教师资助计划(2015GGJS-104);华北水利水电大学大学生创新性实验计划项目(201622)。

汪志昊(1980—),男,河南潢川人,副教授,博士,从事结构振动控制和健康监测方面的研究。E-mail:wangzhihao916@126.com。

10.3969/j.issn.1002-5634.2016.06.014

TV312;TB122

A

1002-5634(2016)06-0078-05