基于教学优化算法的多元超越回归模型及其在径流预报中的应用

崔东文

(云南省文山州水务局，云南 文山 663000)

基于教学优化算法的多元超越回归模型及其在径流预报中的应用

崔东文

(云南省文山州水务局，云南 文山 663000)

基于超越方程内涵,提出多元超越回归(MTR)预报模型。通过4个典型测试函数对新型智能算法——教学优化(TLBO)算法进行仿真验证,并与粒子群优化(PSO)算法、差分进化(DE)算法、萤火虫(FA)算法、布谷鸟搜寻(CS)算法、混合蛙跳算法(SFLA)进行对比分析。利用TLBO算法寻优MTR模型参数,提出TLBO-MTR预报模型,并构建TLBO-支持向量机(TLBO-SVM)、TLBO-BP神经网络(TLBO-BP)、TLBO-多元二项式回归(TLBO-MBR)预报模型作对比;以云南省西洋站和董湖站12月份月径流预报为例,进行实例验证。结果表明:①TLBO算法收敛精度优于PSO、DE、FA、CS和SFLA算法,表现出较好的收敛精度和全局寻优能力；②TLBO-MTR模型对于西洋站和董湖站10年预报的平均相对误差绝对值分别为5.59%、6.60%,均优于TLBO-SVM、TLBO-BP和TLBO-MBR预报模型,表现出较好的预报精度。TLBO-MTR模型预报方法可为水文预测预报提供新的途径,具有良好的应用前景。

径流预报;教学优化算法;多元超越回归;参数优化

探索研究具有较好预报效果的模型及方法一直是水文预测预报中的热点和难点。由于水文预测预报的复杂性、非线性、系统性和不确定性,使得传统回归分析法、成因预测法、数理统计法等方法往往难以达到理想的预报效果。传统回归分析法虽然简单,但预报精度与新兴的小波分析[1]、人工神经网络[2-5]、集对分析[6]、灰色预测[7-8]、支持向量机[9-12]、组合预测[13-14]等方法相比尚显不足。超越方程是指含有未知变量的对数函数、指数函数、三角函数、反三角函数等方程,可用于表征复杂的系统过程。基于超越方程内涵,提出指数型多元超越回归(Multiple Transcendence Regression,MTR)径流预报模型:

(1)

式中:Y为预报对象;X为预报因子;α为待优化指数参数,为一定区间内的实数。

从式(1)可以看出,预报对象Y预报精度的高低,除取决于预报因子X与预报对象Y的相关性外,待优化指数参数α对预报结果的影响也至关重要。超越方程的实根求解是科学技术和工程实践中较难解决的数学问题,传统求解超越方程实根的方法有对分法、牛顿法、弦截法等,这些方法不但求解条件要求高,而且对于复杂的水文预报问题更显得无所适从[15]。目前,遗传算法[16](Genetic Algorithm,GA)、粒子群优化(Particle Swarm Optimization,PSO)算法[15]和森林竞争算法(Forest Competition Algorithm,FCA)[17]等智能算法被尝试用于超越方程实根的求解,并取得了较好的求解效果。然而,对于复杂的参数优化问题,传统GA、PSO算法等智能方法普遍存在收敛精度不高和易陷入局部极值等不足。教学优化(Teaching-Learning-Based Optimization,TLBO)算法[18]是Rao等人于2012年提出的一种新型智能优化算法。该算法灵感源于教师对学生教学过程的抽象,即教师通过对学生的“教学”和学生之间“相互学习”两个阶段来提高整个班级的成绩。TLBO算法具有调节参数少、收敛精度高和全局寻优能力强等特点,在参数识别[19]、BP神经网络权阈值优化[20]等领域得到应用。

本文利用TLBO算法优化MTR模型参数,提出TLBO-MTR径流预报模型,以云南省西洋站和董湖站12个月月径流预报为例进行实例验证。主要作法为:①通过Sphere、Griewank、Rastrigin和Ackley 4个典型测试函数对TLBO算法进行验证,并与PSO算法、差分进化(Differential Evolution,DE)算法、萤火虫算法(Firefly Algorithm,FA)、布谷鸟搜寻(Cuckoo Search,CS)算法、混合蛙跳算法(Shuffled Frog Leaping Algorithm,SFLA)寻优结果进行对比,以验证TLBO算法的寻优能力；②构建TLBO-支持向量机(Support Vector Machines,SVM)、TLBO-BP神经网络(Back-Propagation Network,BP)、TLBO-多元二项式回归(Multivariate Binomial Regression,MBR)预报模型作为TLBO-MTR模型的对比模型,并将之用于同一实例,以验证TLBO-MTR模型的预报精度和泛化能力。

1 TLBO算法

TLBO算法主要模拟班级的“教”与“学”两个过程,教师将自己所学教给学生,提高了整个班级的平均成绩;学生通过向教师学习以及学生之间互相沟通、互相学习提高了整个班级的创造性,从而促进学生个人成绩的提升[21-22]。TLBO算法主要涉及“老师”、“学生”和“班级”几个概念。

1)班级:所有学生(搜索粒子)的集合,集合的平均解记为Xmean;

2)学生:班级中的任意个体(搜索粒子),表示为Xi=[xi1,xi2,…,xid];

3)教师:当前代适应度最好的个体定义为教师,表示为Xteacher。

TLBO算法的“教”阶段是教师将自己的“知识”传递给学生,“传递的知识”由Xteacher和班级的平均值Xmean的差值以及教师的教学因子共同构成;班级每个学生从教师处随机获取“知识”。

设一个d维的待优化目标函数f(x),第i个学生的位置记为Xi=[xi1,xi2,…,xid],当前代最优适应度记为Xteacher;当前代群体平均解记为Xmean;则“教”阶段用式(2)—(4)进行描述:

Xi,new=Xi,old+r1(Xteacher-TFXmean)，

(2)

(3)

TF=rand([1,10])。

(4)

式中:Xi,new、Xi,old分别表示第i个学生的新位置及上一代位置;TF为1～10范围内的随机整数;r1=rand(0,1),为学习步长。

TLBO算法中的“学”阶段是指学生间的互相学习,学生通过分析自已和其他学生的差异进行学习。“学”阶段可描述为:对于学生Xj,从群体中随机选择个体k进行学习,如果f(Xj)优于f(Xi),则:

Xj,new=Xj,old+rj(Xj-Xk)。

(5)

否则,

Xj,new=Xj,old+rj(Xk-Xj)。

(6)

式中r为0～1的随机数。

2 算法验证

为客观评价TLBO算法性能,利用Sphere、Griewank、Rastrigin和Ackley 4个典型高维函数对TLBO算法进行仿真验证,并与PSO、DE、FA、CS、SFLA算法寻优结果进行对比,见表1。

表1 基准函数

其中,Sphere函数用于测试算法的收敛速度;Griewank函数用于测试算法对全局与局部搜索能力的平衡性能;Rastrigin函数用于测试算法的全局搜索能力;Ackley函数用于测试算法跳出局部极值的能力。每个测试函数均独立运行20次,分别求出最优值、最劣值、平均值和标准差4个方面,对此4种算法进行评估,结果见表2。

参数设置:设置TLBO算法最大迭代次数T=2 000,群体规模N=50,TF为1～10的随机整数。设置PSO算法最大迭代次数T=2 000,种群规模N=50,ω=1,ω衰减系数为0.99,局部学习因子、全局学习因子c1=c2=2.0,个体速度限制为[-0.2,0.2]。设置DE算法最大迭代次数T=2 000,种群规模N=50,上下限的尺度因子分别为0.8、0.2,交叉率CR=0.2。设置FA算法最大迭代次数T=2 000,种群规模N=50,最大吸引度β0=2、光强吸收系数γ=1、步长因子α=0.2。设置CS算法最大迭代次数T=2 000,鸟窝位置数N=25、发现概率pa=0.25。设置SLFA算法最大迭代次数T=2 000,青蛙群体规模N=50,子群数M=5,子群内青蛙个数P=10; 子群数局部进化次数T1=10。

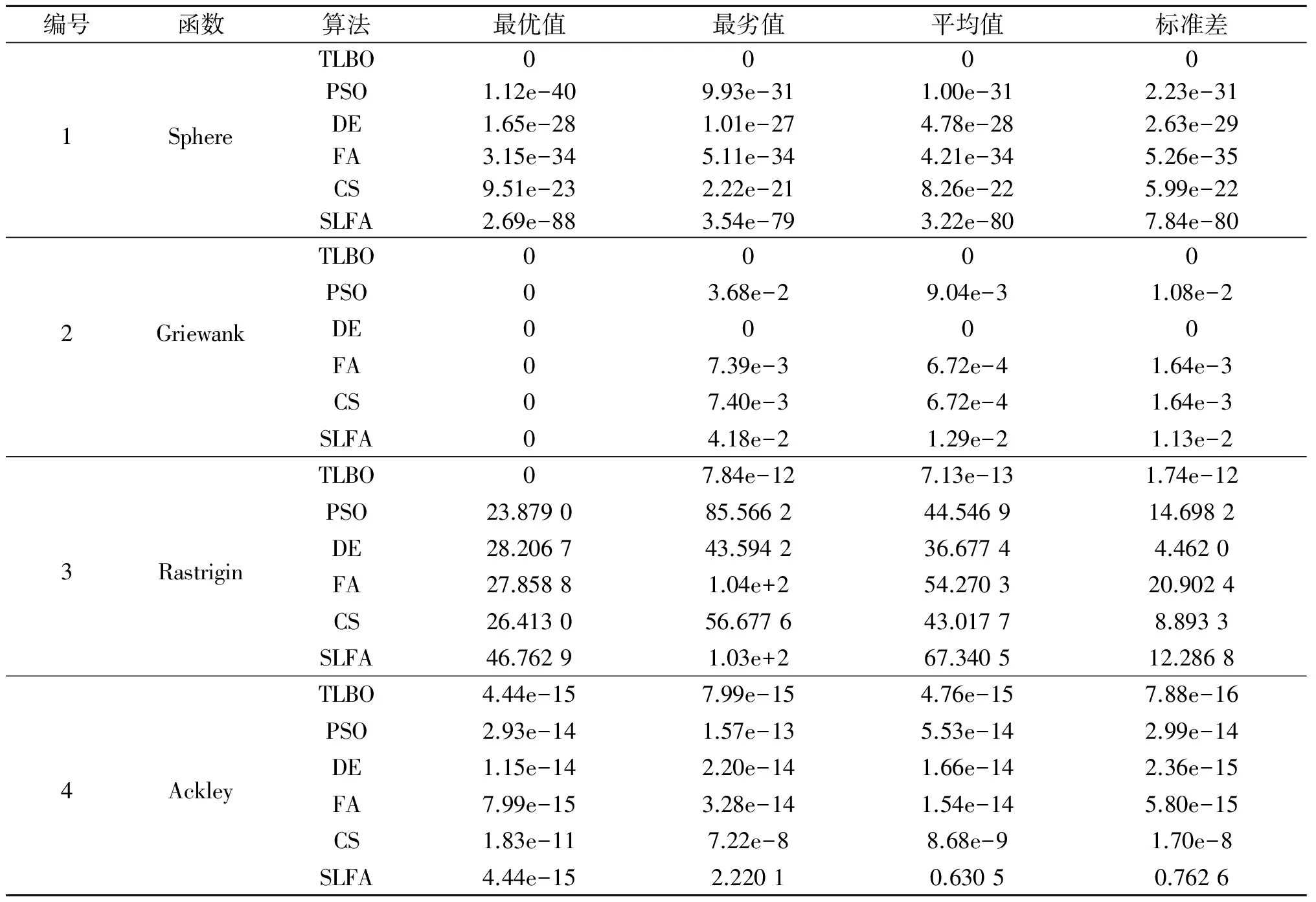
表2 函数优化对比结果

从表2可以看出:

1)对于Sphere函数,TLBO算法与PSO、DE、FA、CS和SLFA算法均获得了较好的寻优效果。相对而言,TLBO算法的寻优获得了理论全局最优解,精度远远优于SLFA、FA、PSO、DE和CS算法(所对比的5种算法的寻优精度由优至劣,下同),表现出较好的收敛速度。对于Griewank函数,TLBO算法与DE算法均获得了理论全局最优解,寻优效果优于FA、CS、PSO和SLFA算法,表现出较好的搜索平衡能力;对于复杂函数Rastrigin, TLBO算法寻优精度优于DE、CS、PSO、FA和SLFA算法13个数量级以上,表现出较好的全局寻优能力;对于Ackley函数,TLBO算法与DE、FA和PSO算法均获得较好的寻优效果,相对而言,TLBO算法的寻优精度要优于DE、FA和PSO算法,远远优于CS和SLFA算法,具有较好跳出局部极值的能力。

2)从4个典型测试函数的寻优结果及比较分析来看,TLBO算法寻优效果优于PSO、DE、FA、CS和SLFA算法,表现出较好的收敛速度、搜索平衡能力和全局寻优能力。

3 TLBO算法优化MTR、SVM、BP和MBR模型参数的实现步骤

本文提出的多元超越回归(MTR)预报模型见式(1);SVM、BP模型基本原理可分别参阅文献[10,23]及文献[24-25];多元二项式回归(MBR)采用纯二次模型,见式(7)。

(7)

式中:Y为预报对象;X为预报因子;β为待优化参数,为一定区间内的实数。

TLBO算法优化MTR、SVM、BP和MBR模型参数的实现步骤可归纳如下:

步骤1 选取训练样本和检验样本,对于SVM、BP模型采用式(8)进行归一化处理。设定MTR、SVM、BP和MBR模型参数的搜寻范围。

(8)

步骤2 确定目标适应度函数。MTR、MBR模型以式(9)作为目标适应度函数;SVM、BP模型以式(10)作为目标适应度函数。

(9)

(10)

步骤3 初始化班级每个学生位置;并设置算法最大迭代次数T,群体规模N,各种待优化模型参数维数。

步骤4 基于训练样本,计算各待优化模型对应的所有学生目标适应度函数值,并在群体中选择适应度最佳的个体作为当代学生的教师。

步骤5 按照式(2)—(4)进行教师阶段的迭代过程,接受好的解。

步骤6 按照式(5)—(6)进行学生阶段的迭代过程,接受好的解。

步骤7 重复步骤4—6,直到满足算法结束条件;输出最好解,即各待优化模型最佳参数。

步骤8 将优化得到的各模型最优参数代入MTR、SVM、BP和MBR模型对检验样本进行预报。

4 实例应用

4.1 数据来源

以云南省西洋站1962—2005年及董湖站1959—2005年12月份平均流量为预报对象,利用SPSS软件分析西洋站及董湖站12月份平均流量与1—11月份平均流量相关关系,见表3。

表3 12月份平均流量与1—11月份平均流量相关系数

注:“*”表示在0.05水平(双侧)上显著相关;“**”表示在0.01水平(双侧)上显著相关。

训练样本及检验样本选取如下:对于西洋站,选取0.05水平(双侧)上显著相关的8—11月份平均流量，作为12月份平均流量的预报因子,利用1962—1995年4个预报因子月平均流量作为率定期样本建立模型,预留1996—2005年作为检验(预报)样本;对于董湖站,选取0.05水平(双侧)上显著相关的9—11月份平均流量，作为12月份平均流量的预报因子,利用1959—1995年3个预报因子月平均流量作为率定期样本建立模型,预留1996—2005年作为检验(预报)样本。对于SVM、BP模型利用式(8)进行样本处理;MTR和MBR模型无需样本处理。

4.2 模型构建与参数设置

4.2.1 模型构建

基于Matlab R2011b软件环境,编程构建TLBO-MTR、TLBO-SVM、TLBO-BP和TLBO-MBR模型,分别利用训练样本、检验样本对4种模型相关参数进行率定和模型检验(预报),选取平均相对误差绝对值MRE(%)和合格率(预报相对误差绝对值小于20%为合格)对各模型的预报效果进行评价。

4.2.2 参数设置

TLBO算法最大迭代次数设置为500,其余参数设置同上。其中,MTR模型待优化参数α的搜索空间设置为-2～2;SVM学习参数惩罚因子C、核函数参数g和不敏感系数ε的搜索空间分别设为0.1～1 000、0.1～1 000和0.000 1～0.1,交叉验证参数γ=2;BP模型网络结构设置为4-7-1,隐含层和输出层传递函数分别采用logsig和purelin, 训练函数采用traingdx,学习速率lr为0.01,设定期望误差为0.01, 最大训练轮回为200次,搜索空间为-1～1;MBR模型待优化参数β的搜索空间设置为-50～50。

4.3 预报及评价

利用TLBO-MTR、TLBO-SVM、TLBO-BP和TLBO-MBR模型对西洋站及董湖站1996—2005年12月份平均流量进行预报,预报结果见表4。4种模型拟合-预报的相对误差如图1所示;TLBO算法连续4次运行优化MTR模型参数的进化过程如图2所示;TLBO算法优化MTR模型参数,其表达式见式(11)—(12)。

西洋站:

(11)

董湖站:

.769 3。 (12)

图1 4种模型拟合预测效果

图2 TLBO算法4次连续进化过程

从表4及图1—2可以看出:

1)从MRE看,无论是训练样本还是检验样本, TLBO-MTR模型均优于TLBO-SVM、TLBO-BP和TLBO-MBR模型;从合格率上看,对于检验样本, TLBO-MTR、TLBO-BP模型均达到100%,高于TLBO-SVM和TLBO-MBR模型;对于训练样本, TLBO-MTR模型合格率均高于TLBO-SVM、TLBO-BP和TLBO-MBR模型。对比分析表明, TLBO-MTR模型具有较高的预报精度,可满足中长期水文预测预报的精度要求。

2)从图1看, TLBO-MTR模型拟合-预报效果明显优于TLBO-SVM、TLBO-BP和TLBO-MBR模型。TLBO-SVM、TLBO-BP和TLBO-MBR模型的拟合-预报精度相差不大,相对而言,TLBO-SVM和TLBO-BP模型的预报精度要略高于TLBO-MBR模型。

3)从图2看, 对西洋站和董湖站TLBO算法4次运行均迭代至100代左右时,就收敛到相对全局最优解47.527 8、65.950 1,表现出较好的收敛速度、全局寻优能力和稳健性能。

5 结语

1)为验证TLBO算法的寻优能力,通过4个典型测试函数对TLBO算法及PSO、DE、FA、CS和SFLA算法进行仿真验证及对比分析。结果表明:TLBO算法寻优效果优于PSO、DE、FA、CS和SLFA算法,表现出较好的收敛速度、搜索平衡能力和全局寻优能力。

2)基于超越方程内涵,提出多元超越回归(MTR)径流预报模型,利用TLBO算法优化MTR模型参数,构建TLBO-MTR预报模型,并构建TLBO-SVM、TLBO-BP和TLBO-MBR模型作为对比分析模型,以云南省西洋站和董湖站12月份月径流预报为例进行实例验证。验证结果表明,TLBO-MTR模型预报精度优于TLBO-SVM、TLBO-BP和TLBO-MBR模型,具有较好的预报效果,可满足中长期水文预测预报的精度要求。

3)尝试利用多元超越回归模型进行水文预测预报,取得了不错的预报效果,模型及方法拓展了水文预测预报途径。鉴于水文过程的随机性和复杂性,TLBO-MTR模型的预报机理等有待于进一步研究。

[1]汪丽娜,陈晓宏,李艳.不同径流尺度的小波神经网络预测[J].华南师范大学学报(自然科学版),2013,45(2):104-106.

[2]崔东文.改进Elman神经网络在径流预测中的应用[J].水利水运工程学报,2013,38(2):71-77.

[3]崔东文.多隐层BP神经网络模型在径流预测中的应用[J].水文,2013,33(1):68-73.

[4]任磊,岳春芳,何训江.RBF神经网络模型在金沟河流域径流预测中的应用水资源与水工程学报[J].水资源与水工程学报,2011,22(1):94-97.

[5]李彦彬，尤凤，徐建新，等.河川日径流预报的混沌神经网络模型[J].华北水利水电学院学报，2012，33(4)：19-21.

[6]王延亭,王建群,张玉杰.基于加权秩次集对分析法的年径流预报模型[J].水电能源科学,2012,30(3):17-19,67.

[7]张霞,陈亚宁,黄海龙,等.河川径流的灰色拓扑预测研究:以新疆阿克苏河为例[J].第四纪研究,2010,30(1):216-223.

[8]马建琴，许龙实，师琨.改进型灰色马尔可夫模型在径流预测中的应用[J].华北水利水电学院学报，2012，33(2)：39-42.

[9]崔东文,金波.果蝇优化算法与支持向量机在年径流预测中的应用[J].人民珠江,2015,36(2):29-32.

[10]崔东文.基于多元变量组合的回归支持向量机集成模型及其应用[J].水利水运工程学报,2014,39(1):66-73.

[11]崔东文,金波.基于改进的回归支持向量机模型及其在年径流预测中的应用[J].水力发电学报,2015,34(2):7-14.

[12]崔东文.几种智能算法与支持向量机融合模型在中长期月径流预测中的应用[J].华北水利水电大学学报(自然科学版)，2016，37(5)：51-57.

[13]彭勇,王国利.小波、模糊与统计相关结合的径流预测方法研究[J].南水北调与水利科技,2011,9(4):47-50.

[14]崔东文.多重组合神经网络模型在年径流预测中的应用[J].水利水电科技进展,2014,34(2):59-63.

[15]张安玲.超越方程的优化解法[J].数学的实践与认识,2014,44(22):172-176.

[16]田雨波,钱鉴,孟非.电磁领域中复超越方程的遗传算法求解方法[J].哈尔滨工业大学学报,2009,41(1):254-257.

[17]郭改文,黄卡玛.森林竞争算法及在超越方程求解中的应用[J].四川大学学报,2008,40(6):127-132.

[18]RAORV,SAVASNIVJ,VAKHARIADP.Teaching-learning-based optimization:an optimization method for continuous non-linear large scale problems[J].Information Sciences,2012,183(1):1-15.

[19]李瑞国,张宏立,王雅.基于反馈教学优化算法的混沌系统参数辨识[J].计算机应用,2015,35(5):1367-1372.

[20]拓守恒.一种优化神经网络的教与学优化算法[J].智能系统学报,2013,8(4):327-332.

[21]陈得宝,魏华,邹锋,等.模拟退火教学式优化算法[J].计算机应用研究,2014,31(12):3553-3556.

[22]吴展.基于改进TLBO算法的光伏阵列MPPT与分布式拓扑结构研究[D].重庆:重庆大学,2014.

[23]崔东文.人工鱼群算法与支持向量机在枯水期月径流预测中的应用[J].人民珠江,2015,36(3):36-40.

[24]崔东文,黄恩奎.基于回溯搜索优化算法的BP神经网络年径流预测[J].人民珠江,2015,36(5):43-46.

[25]崔东文,金波.基于和声搜索算法的BP神经网络需水预测模型应用研究[J].人民珠江,2015,36(4):128-131.

(责任编辑：宰松梅)

Teaching-learning-based Optimization Algorithm-Multiple Transcendence Regression Model and Its Application in Runoff Forecast

CUI Dongwen

(Yunnan Province Wenshan Water Bureau, Wenshan 663000, China)

Based on the transcendental equation, the model of Multiple Transcendence Regression (MTR) forecast was put forward. Through four typical test functions of intelligent algorithms, the teaching-learning-based Optimization (TLBO) algorithm was validated by simulation, and the Particle Swarm Optimization (PSO) algorithm, Differential Evolution (DE) algorithm, Firefly Algorithm (FA), Cuckoo Search (CS) algorithm, Shuffled Frog Leaping Algorithm (SFLA) were compared and analyzed. The TLBO algorithm was used to find the optimal MTR model parameters, then a TLBO-MTR forecast model was put forward and compared with TLBO-Support Vector Machine (SVM), TLBO-BP neural network (BP), TLBO-Multivariate Binomial Regression (MBR) prediction model in Yunnan Province Xiyang station and Donghu station 12 monthly runoff forecast as an example for case study. The results show that the convergence accuracy of TLBO algorithm is better than that of PSO, DE, FA, CS and SFLA, which can show better convergence accuracy and global optimization ability. The average relative error of the TLBO-MTR model for the 10-year forecast of the Xiyang station and Donghu station is 5.59% and 6.60% respectively, which is better than the TLBO-SVM, TLBO-BP and TLBO-MBR forecasting models. The model and method can provide a new way for hydrological forecasting, and it has a good application prospect.

runoff forecasting; Teaching-Learning-Based Optimization (TLBO) algorithm; Multiple Transcendence Regression (MTR); parameter optimization

2016-03-13

崔东文(1978—),男,云南玉溪人,教授级高级工程师,主要从事水资源与水环境方面的研究。E-mail:cdwgr@163.com。

10.3969/j.issn.1002-5634.2016.06.011

TV213

A

1002-5634(2016)06-0061-06