基于灰信息的黄河冰凌灾害风险评估模型

罗党, 刘敏

(华北水利水电大学,河南 郑州 450045)

基于灰信息的黄河冰凌灾害风险评估模型

罗党, 刘敏

(华北水利水电大学,河南 郑州 450045)

为提高黄河冰凌灾害风险评估的可靠性,提出了一种前景理论和集对分析相结合的评估方法,并应用到黄河宁蒙河段的冰凌灾害风险评估中。定义了前景价值函数和概率权重函数;计算了宁蒙河段各分河段的联系向量距离并以其总偏差最大化建立了优化模型,求解了准则权系数;以各分河段相对于正理想方案的贴近度大小进行排序。结果表明:青铜峡—石嘴山河段较易发生冰塞,三湖河口—头道拐河段不易发生冰塞,此结果可为这些河段的防凌防汛工作提供参考。

冰凌灾害；风险评估;灰信息;前景理论;集对分析;黄河宁蒙河段

黄河弯曲多变的河道形态和部分河段低纬度向高纬度的流向,造成了黄河流域很具特色的自然灾害现象——凌汛[1],冰凌灾害的发生会给人们及社会带来巨大的灾难。黄河上游的宁蒙河段和下游的河南—山东河段，河流流向都是从低纬度流向高纬度。当上游解冻开河、下游仍处于封冻状态时,上游开河的冰凌碎块在急弯、卡口等狭窄河段极易形成冰塞现象。影响冰塞现象发生的主要因素有河道形态、河流动力和热力等。当冰塞现象发生时,冰凌、流冰阻塞,造成过流面积减少,致使水位陡涨,出现水鼓冰裂、冰凌漫堤的情形,形成凌灾[2],其危害程度常常超过洪灾。

近年来，我国针对黄河的防凌防汛做了很多工作。2010年，段高云[3]分析了龙羊峡、刘家峡两水库运行前后黄河内蒙古河段的凌汛特点和水沙条件的变化规律，并对内蒙古河段的防凌和防洪需求进行了研究;2011年，刘东常等[4]针对黄河冰塞、冰坝的问题,提出了在冰盖结构上开凿一条冰渠的新思路和在冰下进行爆破使冰体材料发生振动折裂的破冰新理念;2012年，Chen等[5]将高分辨率的遥感卫星数据应用到黄河防凌监测中，初步实现了凌情发展预估、封开河期间的冰凌险情监测，及发生凌汛灾害时灾情信息的采集与评估;2015年，Wu等[6]分析了黄河冰凌水文状况的特点、冰凌演化条件和气象条件，构建了黄河冰凌灾害风险评价模型;2015年，刘晓岩[7]分析了2015—2016年的黄河防凌形势，并提出了多项防凌措施。本文深入分析黄河发生冰凌灾害的可能程度，可为控制灾害的发生和风险的管理提供有效的方法，以达到快速应对灾情、减轻灾害程度的目的。

随机多准则决策[8]问题是指决策者所面临的自然状态为随机出现的一类不确定性决策问题,主要体现为准则值为随机变量。当属性状态概率为区间灰数时，灰色随机多准则决策问题也称为灰色风险型决策[9]问题，具有灰性和随机性两种特性。黄河冰凌灾害的发生具有频发性、突发性、不确定性等特点,且黄河的流量、气温等水文指标也都具有不确定性,这种不确定性正体现出灰色随机多准则决策问题的灰性和随机性特性。由于凌汛或其他自然灾害发生的概率不同,这使得决策评估者面临一定的评估风险,因而本文引入了前景理论[10]。前景理论能很好地反映决策评估者的主观风险偏好,将可能结果的价值转化为整体价值。为了解决整体价值的不确定性,进而引入能很好处理决策择优排序问题的集对分析[11]。集对分析是一种新的处理不确定性问题的数学工具，它将某个数学问题视为一个确定性和不确定性共存系统,在这个系统中,确定性与不确定性相互联系、相互影响、相互制约,并在一定条件下相互转化。通过引入联系数来描述各种不确定性,从而将不确定性转化成便于运算的数学形式。

据此,本文提出了基于灰信息的黄河冰凌灾害风险评估模型,不仅能处理黄河冰凌灾害风险决策问题中数据的灰性和随机性,还考虑到决策评估者的风险偏好,使各分河段冰塞现象的决策评估结果与实际更加相符。

1 基于灰信息的风险评估模型

1.1 问题描述

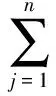
1.2 模型的建立

1.2.1 前景价值函数和前景概率权重函数

P(⊗1⊗2)；

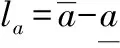
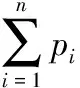
定义3 前景价值是由“价值函数”和“决策权重”共同决定的。考虑到一般参考点的确定方法会受到数据本身和决策者行为的影响,则选取期望作为参考点确定的前景矩阵,各准则下各方案的前景值为:

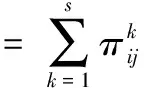
(1)

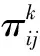
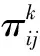
(2)

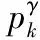
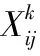
(3)

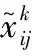
文献[15]指出,当前景价值函数和前景概率权重函数中的参数取为α=β=0.88、θ=2.25、γ=0.61、δ=0.69时,这些取值参数与经验数据相一致。

1.2.2 三元联系数及联系向量距离

定义4[16]给定两个集合A和B,它们的组成集对为H=(A,B)。在某一具体问题背景下,对集对H的特性展开分析,建立了集对H在问题背景下的三元联系数-=a+bi+cj。式中：a为同一度,表示两个集合的同一程度;b为差异度,表示两个集合的差异不确定性;c为对立度,表示两个集合的对立程度;a+b+c=1,a,b,c∈[0,1];i表示差异，j表示对立，i,j∈[-1,1]。

定义5[17]设集合A0与Bs的联系向量为μs=(as,bs,cs)；集合A0与Bk的联系向量为μk=(ak,bk,ck)。则集合Bs与Bk的联系向量距离为：

对于由前景值构成的决策矩阵,每个方案的前景值有正有负,也有交叉项。考虑到前景值应越大越好,因此在不改变不确定信息的条件下，将前景值进行平移或对称变换,得到变换后的前景决策矩阵，并根据定义4得到三元联系数矩阵:

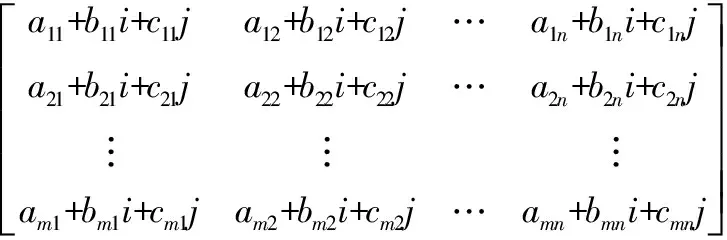
(4)

根据三元联系数中同一度和对立度的大小确定正、负理想方案。由于区间灰数的不确定性和区间灰数之间的对立性,即无关联性,变换后的前景值应越小越好。因此综合考虑，定义三元联系数中同一度和对立度均最小时对应的准则值为正理想方案,相反则为负理想方案。正、负理想方案的表达式为：

(5)

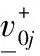
所对应的决策值。

(6)

1.2.3 决策权重的确定及排序

考虑到方案与正理想方案联系向量距离的偏差应越大越好，与负理想方案联系向量距离的偏差应越小越好,将方案与正、负理想方案之间的联系向量距离偏差最大作为目标函数。由于各方案的优劣只有在相同的条件下才能分辨出来,因此构建以下优化模型:

(7)

其中λ一般情况下取0.5。

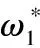
(8)

对各评估对象进行排序,ci越大，评估对象越优。

1.3 评估模型的实现步骤

步骤1 对决策矩阵进行规范化处理,由定义2计算期望值并构成期望矩阵;

步骤2 依据式(1)—(3)确定前景矩阵，并对其进行变换处理;

步骤3 根据式(4)计算三元联系数矩阵,并由式(5)确定正、负理想方案;

步骤5 将准则权重系数代入式(6),并依据式(8)计算各方案相对正理想点的贴近度,对评估对象进行排序。

2 实例分析

黄河地处北回归线以北，全长约5 464 km，走势呈“几”字形，这种特殊的走势使得黄河冰凌灾害问题比较严重，尤其是宁蒙河段。宁蒙河段位于黄河流域的最北端，西起甘肃省和宁夏回族自治区交界的黑山峡，东至内蒙古自治区准格尔旗马栅镇的小占村。由于黄河宁蒙河段属于大陆性季风气候，冬季寒冷而干燥，日平均气温在0 ℃以下的天数较多，日最低气温可达-35 ℃。

黄河宁蒙河段封河时从下游溯流而上，开河期一般从上游向下游解冻。由于黄河上游流经黄土高原和沙漠边缘,导致河水含沙量增大,河道中形成许多浅滩、弯道。当上、下游气温变化幅度增大时，流凌时期易形成冰花和碎冰，而这些冰花和碎冰在移动过程中遇到浅滩、弯道时便容易发生冰塞现象。近年来，受全球气象形势的影响，我国极端天气频繁出现，这使得冰凌灾害越发严重，灾害所造成的财产损失也越来越大。所以，为保护黄河的生态文明、人民的生命财产安全以及减少冰凌灾害的损失，研究黄河的冰凌灾害风险评估显得十分必要。

本文将宁蒙河段分为4个分河段，分别为：青铜峡—石嘴山河段、石嘴山—巴彦高勒河段、巴彦高勒—三湖河口河段、三湖河口—头道拐河段，并分别用a1、a2、a3、a4代表以上4个分河段。根据宁蒙河段河道封冻初期的流凌情况来判断4个分河段可能发生的冰塞状况，提前为防凌防汛做好准备。选取2003—2016年4个分河段流凌期的流量、气温、河道弯度和过水断面4个指标的决策数据进行分析，具体数据见表1。4个分河段的不完全确定权重信息为:

0.10≤ω1≤0.23;

0.20≤ω2≤0.31;

0.19≤ω3≤0.27;

0.15≤ω4≤0.22。

自然状态下，凌汛发生的概率为:

高:p1(⊗)∈[0.21,0.30]；

中:p2(⊗)∈[0.37,0.50]；

低:p3(⊗)∈[0.15,0.26]。

以此为标准确定易发生冰塞现象的河段。

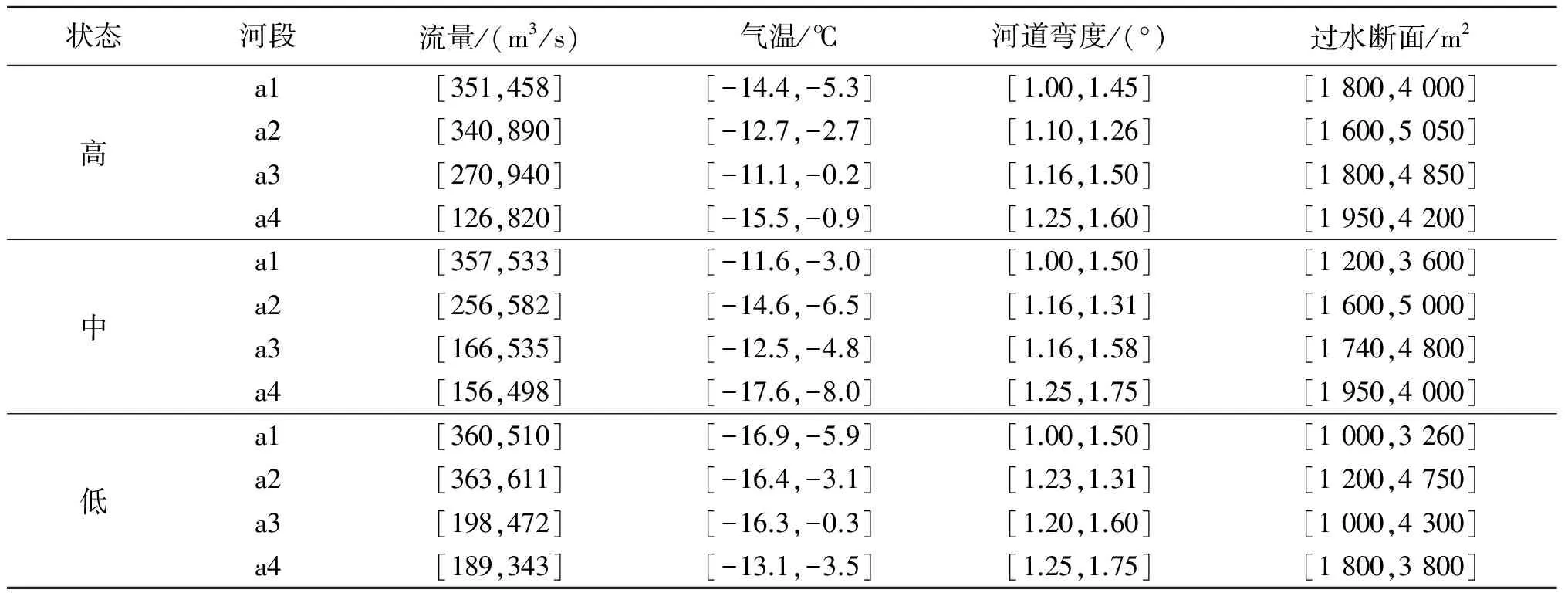
表1 不同状态下各分河段的准则信息

针对此案例分析的求解过程如下:

步骤1 应用文献[12]的规范公式对表1进行规范化处理，得到的规范化决策矩阵见表2。其中流量、气温、过水断面为效益型准则,河道弯曲度为成本型准则。由定义3得到i个评估对象的期望值并构成矩阵，详见表3。

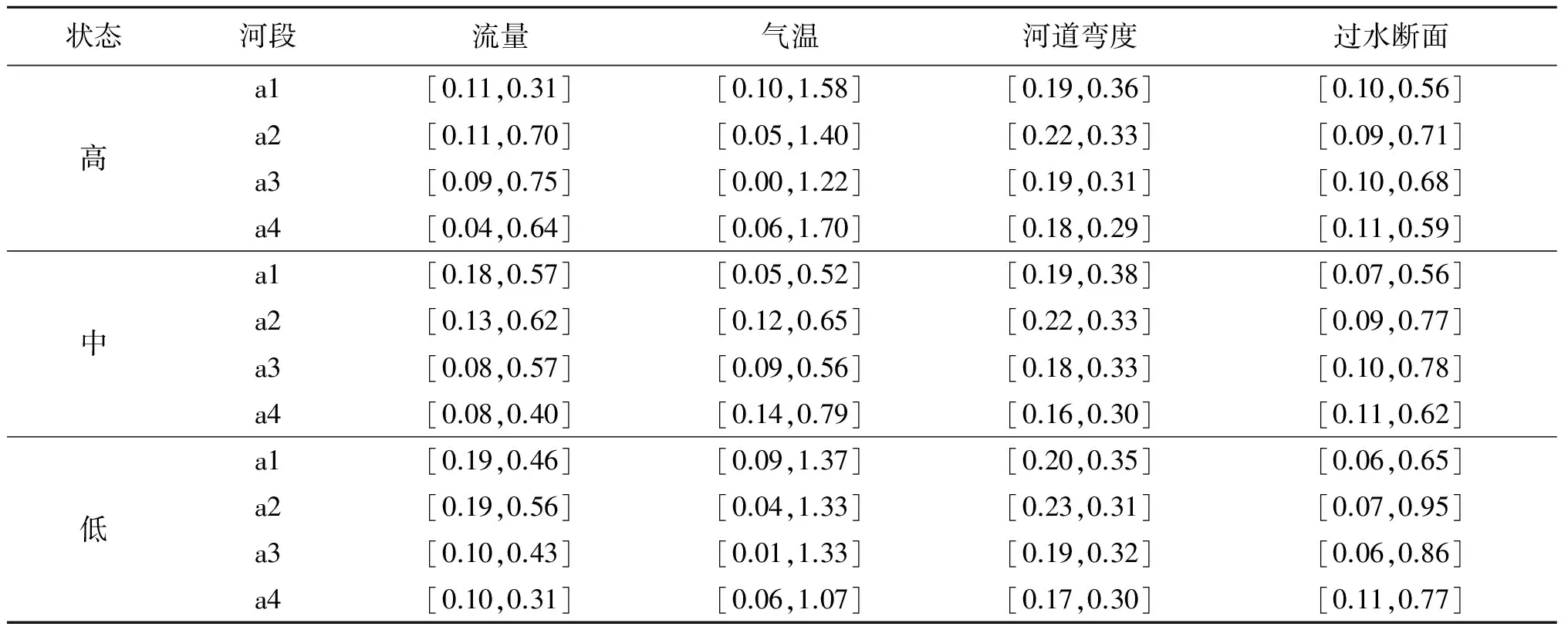
表2 准则信息表的规范化决策矩阵

表3 河段的期望矩阵

步骤2 以期望为参考点,通过式(1)—(3)推求方案的前景矩阵，结果见表4。进而对前景矩阵进行变换得到表5。

步骤3 根据定义4得到i个评估对象的三元联系数矩阵，见表6。从而确定评估对象的正、负理想方案为：

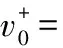
([0.023 9,0.140 0],[0.129 1,0.522 0],

表5 变换后的前景矩阵

表6 三元联系数矩阵

步骤4 根据式(8),利用Lingo软件解得权重向量：

ω*={0.23,0.31,0.24,0.22}。

进而分别求得评估对象与正、负理想方案之间的联系向量距离：

d+={0.098 4,0.129 9,0.110 1,0.137 1}，

d-={0.146 1,0.099 7,0.118 4,0.066 8}。

步骤5 根据式(9)求得评估对象相对正理想方案的贴近度：

C= {C1,C2,C3,C4}=

{0.402 4,0.594 3,0.481 7,0.672 3}。

可知C4>C2>C3>C1,则a4≻a2≻a3≻a1, 即a1河段(青铜峡—石嘴山河段)相对其他3处来说, 更易发生冰塞现象。根据黄河网的历史统计资料显示,在2003—2015年期间,青铜峡—石嘴山河段发生冰塞的次数较多,巴彦高勒—三湖河口河段次之。 由此可知此案例的分析结果与实际相符,说明此方法可行。

为了进一步验证本文介绍方法的合理性和可行性,采用文献[10]提出的方法对上述问题进行验证。验证模型为:

maxZ= 2.856ω1+2.019ω2+

0.721ω3+0.866ω4。

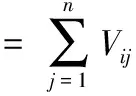
V1=[-2.324 7,-1.348 3];

V2=[-1.931 7,-1.118 9];

V3=[-1.822 1,-1.048 9];

V4=[-2.279 4,-1.319 5]。

又根据区间灰数大小公式，计算得：

P(a2a1)=0.674;

P(a3a1)=0.729;

P(a4a1)=0.519;

P(a3a2)=0.557;

P(a4a3)=0.524。

则

P(a3a1)>P(a2a1)>P(a3a2)>

P(a4a3)>P(a4a1)。

由此可知: a4≻a3≻a2≻a1, 即a1河段相对其他3个河段来说,更易发生冰塞现象。a1河段的验证结果与前文方法的计算结果相一致。

由以上两种方法的排序结果可知,a2和a3河段的顺序发生了变化。从表1的数据来看,a3河段相对于a2河段气温偏低、易结冰,流量较小,河道弯度较大,过水断面较小,当气温回升时,碎冰及冰花在流动过程中较易发生冰塞现象。因此综合表1中的数据知，a3河段相对于a2河段较易发生冰塞现象,说明本文的方法更合理。a1河段是游荡型河段,流量小,河道窄,在封冻初期冰花堵塞冰盖前缘而发生冰塞,即a1河段(青铜峡—石嘴山)更易发生冰塞现象。

3 结语

根据黄河水文信息的特点,构建前景理论和集对分析相结合的评价模型,对黄河宁蒙河段的4个分河段发生冰凌灾害的可能性进行评估。结果表明:青铜峡—石嘴山河段较易发生冰塞,三湖河口—头道拐河段不易发生冰塞。因此，青铜峡—石嘴山河段的防灾及管理措施应放在第一位。提出的前景理论和集对分析相结合的评估方法不仅能提高黄河冰凌灾害风险评估的可靠性，而且还考虑到决策评估者的风险偏好因素,实现了客观和主观的有效结合,使评估结果更加符合实际情况。黄河冰凌生消演变规律复杂,且带来的危害性较大,可根据收集到的凌情数据提前做好风险评估管理和防灾方法筹划，以保障沿河人民群众的生命财产安全。

[1]周龙,周斌卿.黄河内蒙古段凌汛特点及对防凌工作的探讨[J].内蒙古水利,2013(6):96-97.

[2]王富强,王雷.近10年黄河宁蒙河段凌情特征分析[J].南水北调与水利科技,2014,12(4):21-24.

[3]段高云.黄河内蒙古河段防凌防洪运用方式研究[J].人民黄河,2010,32(11):27-28.

[4]刘东常,孟闻远,谢巍,等.黄河冰塞冰坝防治研究新思路[J].华北水利水电学院学报，2011,32(2):1-4.

[5]CHEN L,YANG Z H,HAO L M,et al.Monitoring Yellow River ice disaster based on Chinese high-resolution satellite data[J].Science of Surveying & Mapping,2012,37(4):61-63.

[6]WU C G,WEI Y M,JIN J L,et al.Comprehensive evaluation of ice disaster risk of the Ningxia-Inner Mongolia Reach in the upper Yellow River[J].Natural Hazards,2015,75(2):179-197.

[7]刘晓岩.2015—2016年度黄河防凌形势及防御措施[J].中国防汛抗旱,2015,25(6):1-5.

[8]周欢,王坚强,王丹丹.基于Hurwicz的概率不确定的灰色随机多准则决策方法[J].控制与决策,2015,30(3):556-560.

[9]LIU P,JIN F,ZHANG X,et al.Research on the multi-attribute decision-making under risk with interval probability based on prospect theory and the uncertain linguistic variables[J].Knowledge-Based Systems,2011,24(4):554-561.

[10]王坚强,周玲.基于前景理论的灰色随机多准则决策方法[J].系统工程理论与实践,2010,30(9):1658-1664.

[11]王坚强,龚岚.基于集对分析的区间概率随机多准则决策方法[J].控制与决策,2009,24(12):1877-1880.

[12]宋捷,党耀国,王正新,等.正负靶心灰靶决策模型[J].系统工程理论与实践,2010,30(10):1822-1827.

[13]罗党.基于正负靶心的多目标灰靶决策模型[J].控制与决策,2013,28(2):241-246.

[14]王坚强,任世昶.基于期望值的灰色随机多准则决策方法[J].控制与决策,2009,24(1):39-43.

[15]TVERSKY A,KAHNEMAN D.Advances in prospect theory:cumulative representation of uncertainty[J].Journal of Risk & Uncertainty,1992,5(4):297-323.

[16]田景环,于昊明,亢晓龙.改进的集对分析法在水质评价中的应用[J].华北水利水电大学学报(自然科学版),2015,36(6):20-23.

[17]吕智颖,郑理伟,黄天民,等.一种基于集对分析的模糊多属性决策方法[J].数学的实践与认识,2014,44(16):180-185.

(责任编辑：张陵)

Risk Assessment Model of Ice Disaster in the Yellow River Based on Grey Information

LUO Dang, LIU Min

(North China University of Water Resource and Electric Power, Zhengzhou 450045, China)

In order to improve the reliability of the risk assessment of ice disaster in the Yellow River, an assessment method based on prospect theory and set pair analysis was proposed, and this method was applied to the risk assessment of ice disaster of the reach from Ningxia to Inner Mongolia in the Yellow River. Firstly, the prospect value function and the probability weighting function were defined. Then, the connection vector distance of each reach was calculated, and the optimization model maximized by total deviation of the connection vector distance was built to solve the criteria weights. Finally, the order of reaches can be listed by comparing the close degree between each reach and the positive ideal alternative. The result shows that the reach from Qingtongxia to Shizuishan is prone to ice plug, and the reach from Sanhuhekou to Toudaoguai is not easy. The results can provide a reference for ice and flood prevention work.

ice disaster; risk assessment; gray information; prospect theory; set pair analysis; the reach from Ningxia to Inner Mongolia in the Yellow River

2016-08-04

国家自然科学基金项目(71271086);河南省科技厅重点攻关项目(142102310123);河南省高等学校重点科研项目资助计划项目(15A630005)。

罗党(1959—),男,河南汝南人,教授,博导,博士，主要从事灰色系统理论与决策分析方面的研究。E-mail:iamld99@163.com。

10.3969/j.issn.1002-5634.2016.06.013

TV875;N941.5

A

1002-5634(2016)06-0072-06