具非线性边界耗散和结构阻尼的梁方程的整体解*
王银珠, 杨茂财, 王旦霞
(1. 太原科技大学 应用科学学院, 山西 太原 030024; 2. 太原理工大学 数学学院, 山西 太原 030024)
具非线性边界耗散和结构阻尼的梁方程的整体解*
王银珠1, 杨茂财2, 王旦霞2
(1. 太原科技大学 应用科学学院, 山西 太原 030024; 2. 太原理工大学 数学学院, 山西 太原 030024)
摘要:考虑材料的粘性效应、 介质阻尼和外部阻尼、 转动惯量, 建立了一类更广泛的具有外部载荷的Kirchhoff型非自治梁方程, 研究了其在一定的非线性边界条件和初始条件下系统的初边值问题, 利用经典Galerkin方法, 结合先验估计和Sobolev空间理论, 证明了上述系统的整体解的存在性和唯一性, 为这类梁方程解的合理的Galerkin截断提供了理论依据,也为实际工程提供了设计依据.
关键词:结构阻尼; 转动惯量; 非线性边界; Galerkin方法; 整体解
对于由Woinowsky[1]提出的非线性梁方程
Ball[2]最早对其进行了数学分析, 研究了较一般的非线性梁方程
的整体解的存在性和唯一性. 若考虑阻尼, 可得到具非线性阻尼的非线性梁方程
若既考虑平移运动又考虑转动惯量, 则有
关于这类或更一般的非线性梁方程在齐次边界(零边界)条件下的整体解的存在性, 运用Galerkin方法或经典的算子半群理论方法已被许多学者广泛地研究[3-7]. 对于齐次边界条件下的梁方程系统, Takeda等[8-9]通过将传播算子的扩张公式分解成耗散部分和色散部分, 证明了梁方程
的整体解的存在性. Liang[10]研究了在齐次边界条件下一类具有乘性噪声的阻尼非线性梁方程
的随机爆破解的存在性. 而对于非线性边界条件, 即非齐次边界条件的梁方程系统的整体解的存在性的研究较少. Feireisl[11]和Feckan[12]研究了此方程在非线性边界条件
下的时间周期解的存在性. G. Ji[13]等研究了具有非线性耗散的Kirchhoff型方程系统
的稳定性和能量衰减. Laraya[14]研究了在边界处具有部分阻尼的非线性梁方程
的解的爆破.Fu[15]研究了具有非线性边界条件的粘弹性梁方程系统
的整体解的存在性唯一性和系统能量的指数衰减性.
本文同时考虑了材料的粘性效应、 介质阻尼和外部阻尼、 转动惯量, 建立了一类更广泛的具有外部载荷的Kirchhoff型非线性非自治梁方程
(1)
研究了方程(1)在非线性边界条件
(2)
(3)
和初始条件
(4)
下系统(1)~(4)的整体解u(x,t)的存在唯一性.
1基本空间与假设
本文所考虑的Hilbert空间如下
并分别具有范数‖u‖V=‖uxx‖和‖u‖W=‖uxx‖+‖uxxxx‖.
下面给出非线性函数f,g,σ,φ和外力函数q的假设.
假设 1假设f∶R→R是连续可微函数, 满足
(5)
假设 2假设g∶R→R是连续可微函数, 满足

(6)
其中,ρ>0是一常数.
假设 3假设σ(·)∈C1[0,∞)是非负函数, 满足
(7)
假设 4假设φ(·)∈C1[0,∞)是非负函数, 满足
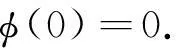
(8)
假设 5外力函数
(9)
2整体解的存在唯一性
本节证明系统(1)~(4)整体解的存在唯一性.
定理假设1~5成立, 对于任意的初始值u0,u1∈W, 且满足相容性条件
(10)
那么系统(1)~(4)存在唯一的解u(x,t)满足
且
证明Step 1(变形系统)考虑系统(1)~(4)的变分问题, 即寻求u(x,t)∈W, 满足
(11)

对于一切ω∈W成立. 下面运用标准的Galerkin逼近方法证明变形方程(11)的解的存在性.

(12)

及初始条件
(13)
式(12)~(13)是一个关于变量t的常微分方程组的柯西问题, 根据常微分方程组解的存在唯一性理论知, 式(12)~(13)在区间[0,tm)上存在唯一的解um(t).由于有界的泛函序列必可取出弱收敛的子序列, 故通过下面的估计后, 逼近解um(t)将被延拖为[0,T]上的整体解, 对于任给的T>0成立.
Step 3(估计)
(14)


根据Gronwall不等式, 得
其中,C在不同的表示式中为不同的任意常数, 因此存在一正常数B1仅仅依赖于T, 对于任意的t∈[0,T] 和任意的m∈N使得
(15)
成立.
(16)
利用Schwarz不等式和平均值不等式,并考虑到初始条件(13), 则存在一正常数B2仅仅依赖于T, 对于任意的t∈[0,T]和任意的m∈N使得
(17)
成立.

(18)
其中
下面估计|J1|和|J2|.
因为边界条件u(0,t)=uxx(0,t)=0,ux(l,t)=0, 因此对于任意的u∈W, 得
(19)
利用分部积分, 得
和
利用中值定理和式(15), 则存在常数C1,C2>0 使得
由式(15),式(19), 并利用Young不等式, 则存在常数C3,C4,C5,C6>0使得
(20)
(21)
又因为f是连续可微函数和考虑到式(19), 则存在常数C7,C8>0使得
(22)
考虑到式(6), 得
(23)
把式(20)~(23)代入式(18), 则存在常数C9>0, 使
(24)
利用Gronwall不等式, 得
(25)
在式(25)两边同除以ξ2, 并令ξ→0取极限, 得
(26)
由估计2, 则存在一常数B3>0仅仅依赖于T, 使得

(27)
Step 4(取极限)由式(15)和式(27), 根据有界的泛函序列必可取出弱收敛的子序列, 通过逼近方程(12)取极限, 从而得到在[0,T]上的整体解的存在性.
Step 5下面说明u(x,t)∈C0([0,∞);V)和u(x,t)∈C1([0,∞);H1(0,l)).
这里先介绍一个引理:假设X是一个Banach空间,X′是其对偶空间,u,g∈L1(a,b;X)且假设对于每一个η∈X′, 在广义导数的意义下有
则称g是u的广义导数, 且u是几乎处处相当于从[a,b]到X的一连续函数.
因为uxx,uxxt∈L2(0,∞;L2(0,l)), 根据此引理得u(x,t)∈C0([0,∞);V), 同理可以证明u(x,t)∈C1([0,∞);H1(0,l)).整体解的存在性得证.
Step 6 (唯一性)假设u,v是系统(1)~(4)具有相同初始值的两个解, 令z=u-v, 有z(0)=zt(0)=0,u,v分别代入变分方程(11), 两式相减, 得
(28)
在式(28)中令ω=zt, 由中值定理, 并考虑到式(15)和(27), 以及Young不等式, 同估计3中的方法, 可得
(29)
由Gronwall不等式, 从式(29)得u=v.唯一性得证.
注下面给出定理中方程系统解的存在唯一性的一个具体例子:即在方程中取σ(s)=α1sγ1,φ(s)=α2sγ2,q(x,t)=sin(x,t),f(s)=β1sγ3-1和g(s)=β2sγ4, 解的存在唯一性定理成立, 其中α1,α2,β1,β2,γ1,γ2,γ3,γ4都是正常数.
参考文献:
[1]Woinowsky-Krieger S. The effect of axial force on the vibration of hinged bars[J]. Journal of Applied Mechanics, 1950, 17(1): 35-36.
[2]Ball J M. Initial-Boundary value problems for an extensible beam[J]. Journal of Mathematical Analysis and Applications, 1973, 42: 61-90.
[3]Ball J M. Stability theory for an extensible beam[J]. Journal of Differential Equations, 1973, 14(3): 399-418.
[4]Fitzgibbon W E. Global existence and boundedness of solutions to the extensible beam equation[J]. SIAM Journal of Mathematical Analysis, 1982, 13(5): 739-745.
[5]Yang Zhijian. On an extensible beam equation with nonlinear damping and source terms[J]. Journal of Differential Equations, 2013, 254(9): 3903-3927.
[6]Ma T F, Narciso V. Global attractor for a model of extensible beam with nonlinear damping and source terms[J]. Nonlinear Analysis, 2010, 73(10): 3402-3412.
[7]Cavalcanti M M, Domingos Cavalcanti V N, Soriano J A. Global existence and asymptotic stability for the nonlinear and generalized damped extensible plate equation[J]. Communications in Contemporay Mathematics, 2004, 6(5): 705-731.
[8]Takeda H, Yoshikawa S. On the initial value problem of the semilinear beam equation with weak damping I: smoothing effect[J]. Journal of Mathematical Analysis and Applications, 2013, 401: 244-258.
[9]Takeda H. Large time behavior of global solutions of the semilinear damped beam equation with slowly decaying data[J]. Journal of Mathematical Analysis and Applications, 2015, 423(2): 898-912.
[10]Liang Fei. Explosive solution of stochastic nonlinear beam equations with damping[J]. Journal of Mathematical Analysis and Applications, 2014, 419(2): 849-869.
[11]FeireislE.Non-zerotimeperiodicsolutionstoanequationofpetrovskytypewithnonlinearboundarycondition:slowoscillationsofbeamsonelasticbearings[J].AnnaliDellaScuolaNormaleSuperiorediPisa, 1993, 20(1): 133-146.
[12]FeckanM.Freevibrationsofbeamsonbearingswithnonlinearelasticresponses[J].JournalofDifferentialEquations, 1999, 154(1): 55-72.
[13]JiG,LasieckaI.NonlinearboundaryfeedbackstabilizationforasemilinearKirchhoffplatewithdissipationactingonlyviamoments-limitingbehavior[J].JournalofMathematicalAnalysisandApplications, 1999, 229(2): 452-479.
[14]LabidiS,TatarN.Blow-upofsolutionsforanonlinearbeamequationwithfractionalfeedback[J].NonlinearAnalysis, 2011, 74(4): 1402-1409.
[15]FuMT.Boundarystablizationforanon-linearbeamonelasticbearings[J].MathematicalMethodsintheAppliedScience, 2001, 24(8): 583-594.
Global Solutions of Beam Equation with Nonlinear Boundary Dissipations and Structural Damping
WANG Yin-zhu1, YANG Mao-cai2, WANG Dan-xia2
(1 College of Applied Science, Taiyuan University of Science and Technology, Taiyuan 030024, China;2. College of Mathematics, Taiyuan University of Technology, Taiyuan 030024, China)
Abstract:Simultaneously, considering the viscous effect of material, damping of medium and external damping, and rotational inertia, a kind of more general Kirchhoff type non-autonomous beam equation with external load was established. Under certain nonlinear boundary conditions and initial conditions, the initial-boundary value problem of the nonlinear non-autonomous beam equation was studied. By using classical Galerkin method, combining the prior estimate and the Sobolev space theory and some inequality skills, the existence and uniqueness of the global solutions for the above-mentioned system were proved. Furthermore, the result provides the theoretical basis for this kind of beam equation reasonable Galerkin truncation, also provides the design basis for the practical engineering.
Key words:structural damping; rotational inertia; nonlinear boundary; Galerkin method; global solutions
中图分类号:O175.27
文献标识码:A
doi:10.3969/j.issn.1673-3193.2016.01.003
作者简介:王银珠(1977-), 男, 讲师, 博士, 主要从事无穷维动力系统与算子代数及量子信息研究.
基金项目:太原科技大学2014年校博士科研启动基金项目; 山西省自然科学基金资助项目(2015011006, 2015011003)
*收稿日期:2014-12-18
文章编号:1673-3193(2016)01-0010-05

