Glauberman-Solomon子群的推广*
靳 平, 曹慧芹, 常学武
(山西大学 数学科学学院, 山西 太原 030006)
Glauberman-Solomon子群的推广*
靳平, 曹慧芹, 常学武
(山西大学 数学科学学院, 山西 太原 030006)
摘要:对任意有限p-群 P, 定义了一个新的特征子群序列 Dspan(P), i≥1, 并证明了当 G 为 p-稳定群时, 如果 P∈Sylspan(G), 则在适当条件下, 每个 Dspan(P) 均为 G 的特征子群. 该结果推广了 Glauberman 和 Solomon 在文献[8]中的主要定理. 进而, 上述结果被推广到了融合系.
关键词:p-群; p-稳定; 融合系
0引言
本文所考虑的群均为有限群, 使用标准符号和术语[1-2], 约定p表示一个任意素数.
设G为有限群,p|G|. 若对每个p-子群Q≤G和g∈NG(Q), 只要 [Q,g,g]=1, 就有
则称G为p-稳定的.p-稳定群是极为重要和广泛的一类群. 例如, 若G是p-可解群, 当p≥5 或p=3 时,G有交换的 Sylow 2-子群, 则G必为p-稳定群[3-5].

设P为p-群, 记Ωi(P)=〈x∈P|xpi=1〉. 为简单计, 称子群A≤P是类 2-自由的, 如果A满足条件: 只要x∈P使得幂零类c(〈A,x〉)≤2, 就有 [A,x]=1. 对i≥ 1, 定义
和Di(P)=〈A|A∈Di(P)〉. 则不难看出

定理 1设 G 为有限群, p 为素数, P∈Sylp(G). 如果 G 是 p-稳定的, 且 CG(Op(G))≤Op(G), 则 Di(P) 都是 G 的特征子群, i≥1.
融合系是一门以范畴化的角度去处理有限群问题的新学科, 与有限群局部理论密切相关, 具有广泛的应用背景, 如拓扑学中的分类空间, 有限群的块理论, 有限单群的分类等. 本文将上述 p-稳定群的概念引入到融合系中, 即定义融合系的 p-稳定性. 设F为 p-群 P 上的饱和融合系, 如果对每个 Q≤P 和每个 φ∈AutF(Q), 只要 [Q,φ,φ]=1, 则 φ∈ Op(AutF(Q)), 则称F为 p-稳定的. 不难看出, 当F=FP(G) 为群融合系时, 则F的 p-稳定性即等价于群 G 的 p-稳定性.
以下是定理 1 在融合系中的推广.
定理 2设F是有限 p-群 P 上 p-稳定的饱和融合系, 则对每个 i≥1, Di(P)◁F.
1预备知识
本节给出融合系的定义及相关概念. 其中定义 1~4[3].
定义 1[2]设 P 为有限 p-群. 称范畴F为 P 上的一个融合系, 如果F的对象集为 P 的所有子群; 对任意 Q, R≤P, 相应的态射集HomF(Q,R) 满足
HomP(Q,R)⊆HomF(Q,R)⊆Inj(Q,R),
其中,HomP(Q,R) 由 P 中元素所诱导的共轭映射构成,Inj(Q,R) 为从 Q 到 R 的全部单同态, 并满足
1) 对任意 φ∈HomF(Q,R), 同构映射 φ∶Q→Qφ 属于HomF(Q,Qφ);
2) 若 φ∈HomF(Q,R) 是同构映射, 则其逆 φ-1∈HomF(R,Q).
对任意 Q≤P, 简记AutF(Q)=HomF(Q,Q). 显然 NP(Q) 可共轭作用在 Q 上, 记AutP(Q) 为 NP(Q) 在Aut(Q) 中的像, 即有AutP(Q)≅NP(Q)/CP(Q). 由融合系定义显然有Inn(Q)◁AutF(Q), 故再记OutF(Q)=AutF(Q)/Inn(Q). 如果存在F-同构 φ∶Q→R, 则称 Q 和 R 为F-共轭.
定义 2[2]设F是有限 p-群 P 上的融合系, Q≤P.
1) 若对 Q 的任意F-共轭 R, 总有 |NP(Q)|≥|NP(R)|, 则称 Q 为fullynormalized子群.
2) 若对 Q 的任意F-共轭 R, 总有 CP(R)=Z(R), 则称 Q 为F-centric子群.
3) 如果 Op(AutF(Q))=Inn(Q), 则称 Q 为F-radical子群.
4) 分别用Ff(Fc,Fr) 表示 P 的fullynormalized(F-centric,F-radical) 子群的全体.
5) 若 Q∈Ffcr=Ff∩Fc∩Fr, 则称 Q 为Alperin子群.
定义 3[2]设 P 为有限 p-群. 称 P 上融合系F为饱和融合系, 如果
1)Inn(P)∈Sylp(AutF(P));

特别地, 若 G 为有限群, P∈Sylp(G), 则存在一个 P 上饱和融合系FP(G): 其对象为 P 的所有子群; 对任意 A, B≤P, 态射集为
其中, cg为 g 诱导的共轭映射;FP(G) 中态射合成为普通映射合成.
类似有限群中的正规化子, 融合系也有正规化子等概念.
定义 4[2]设F为有限 p-群 P 上融合系.
1)F的一个子系E为一个子范畴, 使得E本身构成一个融合系. 若存在 Q≤P 使得E为 Q 上融合系, 则称E为定义在 Q 上的子系.

3) 称 Q≤P 在F中正规, 如果F=NF(Q), 简记为 Q◁F.
4)F中最大的正规子群记为 Op(F). 若F是饱和融合系且 CP(Op(F))≤Op(F), 则称F是约束的.
下面为融合系约束模型定理, 见命题 C[9].
定理 3[9]设F是有限 p-群 P 上的饱和融合系. 若F是约束的, 则存在唯一有限群 G 使得
1) P∈Sylp(G);
2)F=FP(G);
3) Op′(G)=1;
4) CG(Op(G))≤Op(G).
2证明
下面先建立 Di(P) 的两个基本性质.
引理 1[1]1) Ωi(Z(P))≤Di(P).
2) 如果 Di(P)≤T≤P, 则 Di(P)≤Di(T).
证明1) P 的中心 Z(P) 自动满足交换和类 2-自由的条件, Z(P) 的子群 Ωi(Z(P)) 也是交换和类 2-自由, 且 Ωi(Ωi(Z(P)))=Ωi(Z(P)), 所以 Ωi(Z(P))≤Di(P).
2) 任取 A∈Di(P), 则 A 为 T 的交换子群, 也满足类 2-自由条件, 即 A∈Di(T), 从而 Di(P)≤Di(T).
引理 2对任意 i≥1, Di(P) 是Di(P) 中唯一极大的成员.
证明记 D=Di(P), 则只需证明 D∈Di(P). 分下面几步完成证明.
1) D 为交换子群.
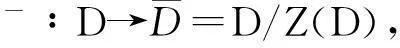
2) Ωi(D)=D.
任取 A∈Di(P), 则 Ωi(A)=A, 故 Ωi(D)=D.
3) D∈Di(P).
任取 x∈ P, 使得 c(〈D,x〉)≤2. 则对任意 A∈Di(P), 显然 c(〈A,x〉)≤2, 根据定义 [A,x]=1, 从而 [D,x]=1, 表明 D∈Di(P).
定理 1 的证明令 D=Di(P), 分下面三步证明.
1) 若 D◁ G, 则 D 在 G 中特征.
事实上, 对任意 σ∈Aut(G), 则 Pσ∈Sylp(G), 故存在 g∈ G 使得 Pσ=Pg. 此时
表明 D 在 G 中特征.
2) 令 Q=Op(G), 则 D≤Di(Q).
由于 Q≤P, 而 D◁ P 为交换子群, 故 [Q,D,D]≤[D,D]=1. 根据 p-稳定性条件, 则 DCG(Q)/CG(Q)≤Op(G/CG(Q)), 再由条件 CG(Q)≤Q, 知
表明 D≤Q≤P. 由引理 1 可知 D≤Di(Q).
3) 令 W=〈Dg|g∈ G〉, 则 W∈Di(P).
因为 Di(Q)charQ◁ G, 所以 Di(Q)◁ G. 故 W≤Di(Q), 表明 W 也是交换群, 并且 Ωi(W)=W. 下面只需验证 W 也是类 2-自由的. 事实上, 设 x∈ P, 满足 c(〈W,x〉)≤2. 显然 [W,x,x]=1. 令 C=CG(W), C1/C=Op(G/C) 则显然 C1◁ G. 根据 p-稳定条件, 有 xC∈ C1/C, 即 x∈ C1. 因为 C1◁ G, 所以 Pg∩ C1∈Sylp(C1), 但因为 C1/C 为 p-群, 则迫使 C1=C(Pg∩ C1). 此时可设 x=cx1, 其中 c∈ C 而 x1∈ Pg∩ C1. 显然 [W,x1,x1]=1, 故 [Dg,x1,x1]=1, 由文献[8]引理 2, 得 c(〈Dg,x1〉)≤2. 按定义可知 [Dg,x1]=1, 亦即 [Dg,x]=1, 导致 [W,x]=1, 表明 W 也是类 2-自由的交换子群, 即 W∈Di(P). 由引理 2 得 Y=W◁ G.
下述结论表明融合系的 p-稳定性对子系遗传.
引理 3设 P 为有限 p-群,F是 P 上的饱和融合系, 并且E是定义在 R≤P 上的子系. 若F是 p-稳定的, 则E也是 p-稳定的.
证明任取 Q≤R, ψ∈AutE(Q), 设 [Q,ψ,ψ]=1. 因为 Q≤P, 显然AutE(Q)≤AutF(Q). 由F是 p-稳定的, 得 ψ∈ Op(AutF(Q))∩AutE(Q)≤Op(AutE(Q)), 表明E是 p-稳定的.
称 W 为一个特征 p-函子, 如果对任意 p-群 P, W(P) 是 P 的一个特征子群, 且对任意群同构 φ∶P→Q, 总有 W(P)φ=W(Q). 若进一步对任意 P>1, 总有 W(P)>1, 则称 W 为正特征 p-函子. 为证明定理 2, 需要下述结论.
引理 4[8]设F是有限 p-群 P 上饱和融合系, W 是正特征 p-函子. 如果对任意 Q∈Ffcr且 1 引理 4 的另一种证明方法,见文献[1]. 定理 2 的证明假设结论不成立, 选取F为一个极小反例: 即先满足 |P| 极小, 再满足 |F| 极小, 其中 |F| 表示F中态射的个数. 记 D=Di(P). 首先验证 D 为正特征 p-函子. 显然 D 是特征 p-函子, 根据定义 只需证 D1(P)>1. 显然 P>1, 故 Z(P)>1. 根据引理 1 可得 1<Ω1(Z(P))≤D1(P). 根据引理 4, 则存在某个 1 参考文献: [1]GlaubermanG,SolomonR.Anewcharacteristicsubgroupofap-stablegroup[J].JournalofAlgebra, 2012, 368: 231-236. [2]IsaacsI.FiniteGroupTheory[M].NewYork:AMS, 2008. [3]CravenD.TheTheoryofFusionSystems[M].London:CambridgeUniversityPress, 2011. [4]GorensteinD.FiniteGroups[M].NewYork:AmericanMathematicalSociety, 2007. [5]HenkeE.RecognizingSL2(q)infusionsystems[J].JournalofGroupTheory, 2010, 13(5): 679-702. [6]MeierfrankenfeldU,StellmacherB. F-stabilityinfinitegroups[J].TransactionsoftheAmericanMathematicalSociety, 2009, 361(5): 2509-2525. [7]GlaubermanG.Acharacteristicsubgroupofap-stablegroup[J].Canad.J.Math., 1968, 20(1): 1101-1135. [8]KessarR,LinckelmannM. ZJ-theoremsforfusionsystems[J].TransactionsoftheAmericanMathematicalSociety, 2008, 360(6): 3093-3106. [9]BrotoC,CastellanaN,GrodalJ,etal.Subgroupfamiliescontrollingp-localfinitegroups[J].Proc.LondonMath.Soc., 2005, 91(3): 325-354. A Generalization of Glauberman-Solomon Subgroups JIN Ping, CAO Hui-qin, CHANG Xue-wu (School of Mathematical Sciences, Shanxi University, Taiyuan 030006, China) Abstract:A new series of characteristic subgroups Dspan(P) and i≥1 is defined for an arbitrary finite p-group P. It is also proved that if G is a p-stable group with P Sylspan(G), then under some appropriate conditions, every Dspan(P) is a characteristic subgroup of G. This generalizes the main theorem of Glauberman and Solomon in [8]. Furthermore, the above result is generalized to fusion systems. Key words:p-group; p-stable; fusion system 中图分类号:O152.1 文献标识码:A doi:10.3969/j.issn.1673-3193.2016.01.004 作者简介:靳平(1964-), 男, 教授, 博士, 主要从事有限群表示论的研究. 基金项目:山西省自然科学基金资助项目 (2012011001-1) *收稿日期:2015-07-09 文章编号:1673-3193(2016)01-0015-04
——以指数、对数函数同构问题为例

