基于CFD的KCS船舶艏部型线优化研究

冯佰威，叶诗瑶，常海超

(1.武汉理工大学 高性能船舶技术教育部重点实验室,湖北 武汉 430063；2.武汉理工大学 交通学院，湖北 武汉 430063)

基于CFD的KCS船舶艏部型线优化研究

冯佰威1，叶诗瑶2，常海超1

(1.武汉理工大学 高性能船舶技术教育部重点实验室,湖北 武汉 430063；2.武汉理工大学 交通学院，湖北 武汉 430063)

为实现基于CFD船体型线优化设计，开发了船体型线优化平台，并以KCS船为初始船型，对其艏部型线进行了优化。首先，重点介绍了径向基函数插值的基本原理及其在船体曲面变形中的应用；其次，将该方法与CFD软件及优化算法结合，开发了基于CFD的船体型线优化平台；最后，将该平台应用于KCS船的艏部型线优化设计，获得给定约束条件下阻力性能最优的船体外形。研究结果表明：基于径向基函数船体曲面修改方法是可行的，建立的船型优化平台具有一定的工程应用价值。

KCS; 径向基插值；CFD；阻力性能；仿真优化

0 引言

随着计算机技术的飞速发展和计算数学理论的不断完善，计算流体力学(Computational Fluid Dynamics，CFD)得到了蓬勃发展，评估能力显著增强，已逐步迈向实用化。最近几届的国际船舶ITTC会议都将基于仿真的设计(Simulation Based Design， SBD)列为数值模拟技术研究的前沿热点课题。这种设计方法将CFD技术和最优化技术直接应用于新船型的设计。利用CFD对设定的优化目标(船舶水动力性能)进行数值计算，同时利用优化算法和船体曲面修改技术对船型设计空间进行探索，最终获得给定约束条件下性能最优的船体外形。

意大利罗马水池的Daniele Peri和INSEAN水池的Campana[1-2]、日本东京大学的Yusuke Tahara[3]等都将数值模拟技术和优化算法结合，实现CAD/CFD的集成，建立了基于CFD的船型优化设计框架，成功完成了船体型线的仿真优化设计,获得了水动力性能较佳的船体外形。为了实现基于CFD的船型优化，本文将径向基函数插值技术应用于船体曲面修改，将该方法与CFD技术及优化算法结合，建立船体型线优化平台，并应用于KCS船的型线优化设计。

1 基于径向基插值的船体曲面修改方法

为满足船舶航行性能的需要，船体曲面往往异常复杂。这类曲面如果由NURBS精确表达，其控制顶点数必然非常多，不仅会给手工修改船体曲面带来巨大的困难，而且更不利于船型优化的研究。为此，国内外的学者一直在探讨船体曲面的参数化修改方法。

目前，船体曲面的参数化修改方法主要分为以下2类：一类是基于母型的融合方法，另一类是直接修改控制顶点坐标的方法。冯佰威等[4]将第一类方法应用到船型优化中。这种方法在母型光顺的条件下，能够保证生成的新船型也光顺，很适用于局部变换。不足之处在于它得到的是船体的整体变形，不能对局部型线开展研究。第二类方法主要包括Peri.D[1]、李胜忠[5-6]的Bezier Patch方法和自由变形法。这类方法可以用于整船的几何重构，但设计变量相对较多并且控制点需要合适的选择。

以上两类方法大体上都是以母型船的NURBS控制顶点为设计参量实现船体曲面变形的。本文以船体曲面的NURBS表达为基础，采用径向基函数插值技术进行船体曲面修改。

1.1 船体曲面NURBS表达

本文采用NURBS曲面来表达船体曲面，对任一NURBS曲面，可由下面的公式来表达：

(1)

式中：u、v为节点向量；m、n为u、v向控制顶点的个数；dij(0≤i≤n,0≤j≤m)为NURBS控制顶点；wi(i=0,1,…，n)为权重因子，分别与控制顶点dij(i=0,1,…，n)相联系；Ni,k(u)和Nj,i(v)为B样条基函数，它的第1个下标i表示B样条的序号，第2个下标k表示B样条的幂次(等于阶数-1)。其由以下递推公式定义：

(2)

可知，当固定u、v向的节点矢量时，船体曲面各点的型值由控制顶点的位置决定，因此，通过修改控制顶点的位置可以实现对曲面形状的修改，生成新的船型。

1.2 基于径向基函数的船体曲面插值

径向基函数(Radial Basis Function，RBF)指某种沿径向对称的标量函数，通常定义为空间中任一点X到某一中心Xi之间欧氏距离的函数。各基函数的形式为：

Φ(‖X-Xi‖)i=1,2,…,n

式中：Xi为函数的中心；Φ以输入空间的点X与Xi中心的距离为自变量，故称为径向基函数。

径向基函数插值法用于船体曲面修改时使用以下形式的插值函数[7]：

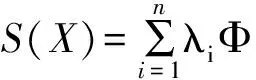
(3)

式中：S(X)表示点X=(x,y,z)在船体曲面上移动的距离；p(X)为低阶多项式，具体形式是：p(X)=c1x+c2y+c3z+c4；n为控制点的个数；‖X-Xi‖表示两点之间的欧氏距离；Φ为给定的基函数。

这里取1种具有紧支撑特性的基函数：Wedndland’s函数的三维形式[7]：当0≤‖x‖<1时，Φ(‖X‖)=(1-‖X‖)4(4‖X‖+1)；当‖x‖为其他值时，Φ(‖X‖)=0。它保证由此构造的系统矩阵是正定矩阵。方程中的系数λi、Ci由控制点坐标的变化得到：

S(Xi)=fi,i=1,2,…,n

(4)

式中：fi表示控制点的变化量。

将n个控制点移动前后的坐标带入上式，再联立权重系数满足正交性质的约束条件[8]：

(5)

式中：pT为p的转置矩阵。

可以得到如下形式的矩阵：

(6)

其中：

λ=[λ1,λ2,…,λn]T,c=[c1,c2,c3,c4]T,f=[f1,f2,…,fn]T

Mi,j=Φ(‖Xi-Xj‖)i,j=1,2,…,n

(7)

通过解方程(6)可求得方程中所有未知系数。

1.3 变形实例

本文采用径向基函数插值的方法对船体曲面进行参数化修改[9]。该方法的优势在于：在进行船体变形时可以固定水线、甲板边线或特定站位间的控制点，使这些部分不发生变化，这样就可以保留住母型船的特定线型，方便工程师在总布置方面的设计。下面以一个具体实例说明。

如图1所示,首先选择船艏部外形轮廓以及设计水线处的控制点作为不变点，其他的 10个控制点为可变点；然后将所有控制点(包括不变的坐标点和变化点)的坐标带入式(3)，解方程可求出所有的待定系数λi和ci；最后将原船体剩余的网格点带入方程就可求得新的网格点的位置，从而获得新的船体型线。由图1的横剖线比较可知，变形前后水线处的线型没有发生改变。

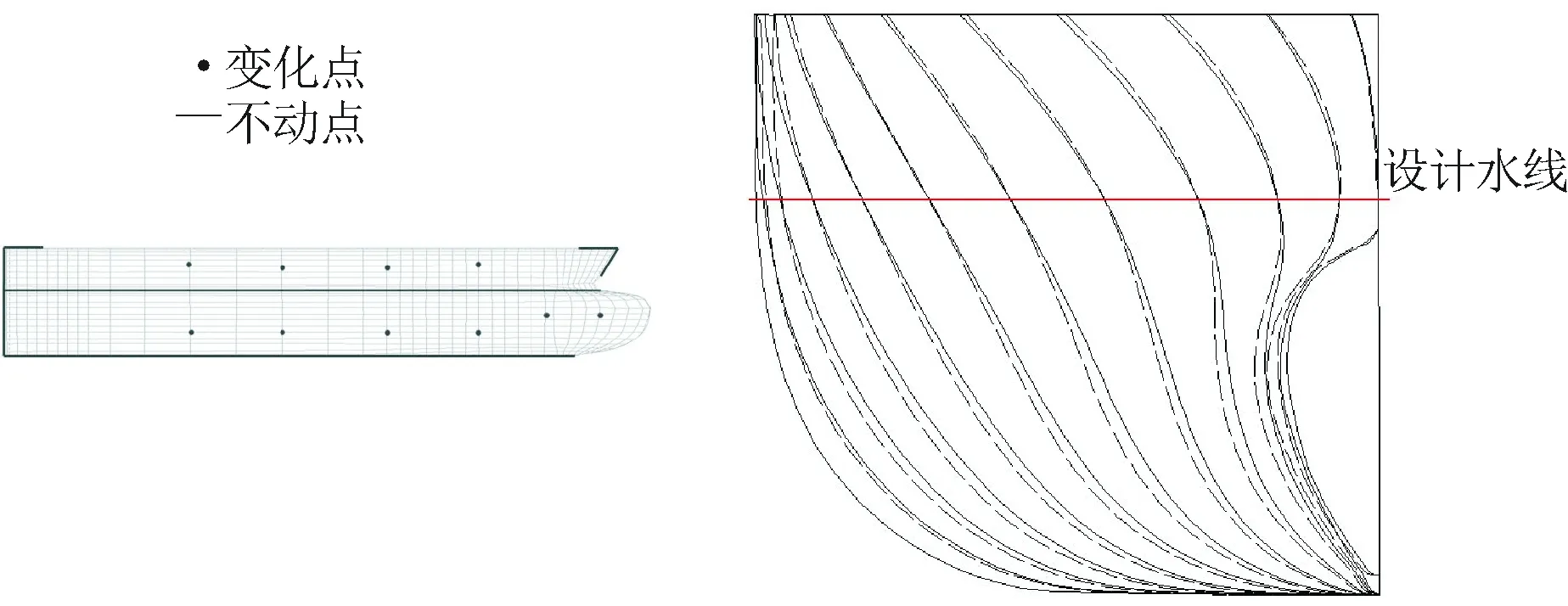
图1 固定水线的艏部变形

同理，选择图2所示的11个控制点为可变点，船艏部外形轮廓以及部分站位线上的控制点作为不变点。调整11个可变控制点，经过径向基插值可得新船型。由图2可知，变形前后船艏部分在8～12站位之间的型线没有发生变化。

2 基于CFD的船体型线优化平台

开发船体型线优化平台是为了给设计人员提供便利环境，以进行船型优化，其主要功能包括：集成多学科的分析流程，定义设计变量、约束和优化目标，提供算法以驱动优化。基于CFD的船体型线优化平台如图3所示。各模块的功能和原理请参考文献[10]。

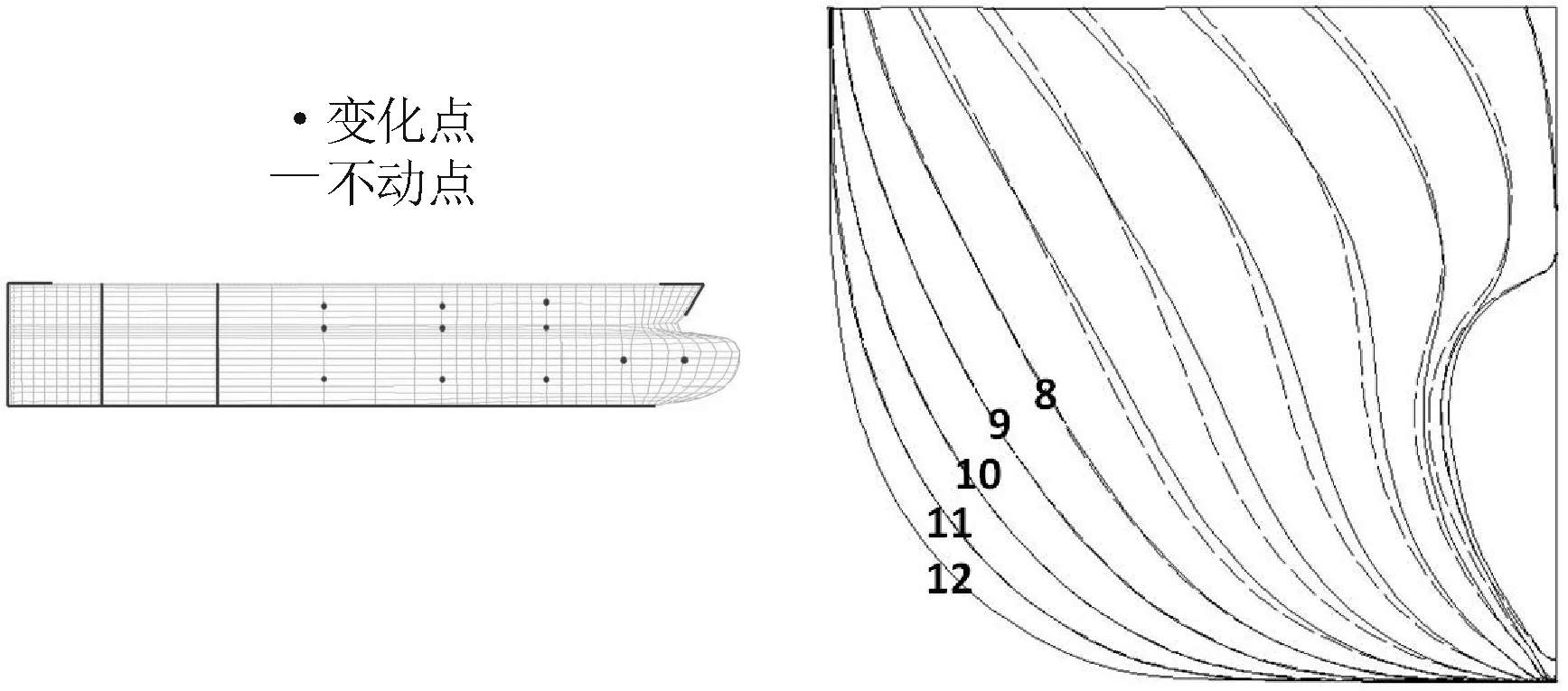
图2 固定站位的艏部变形

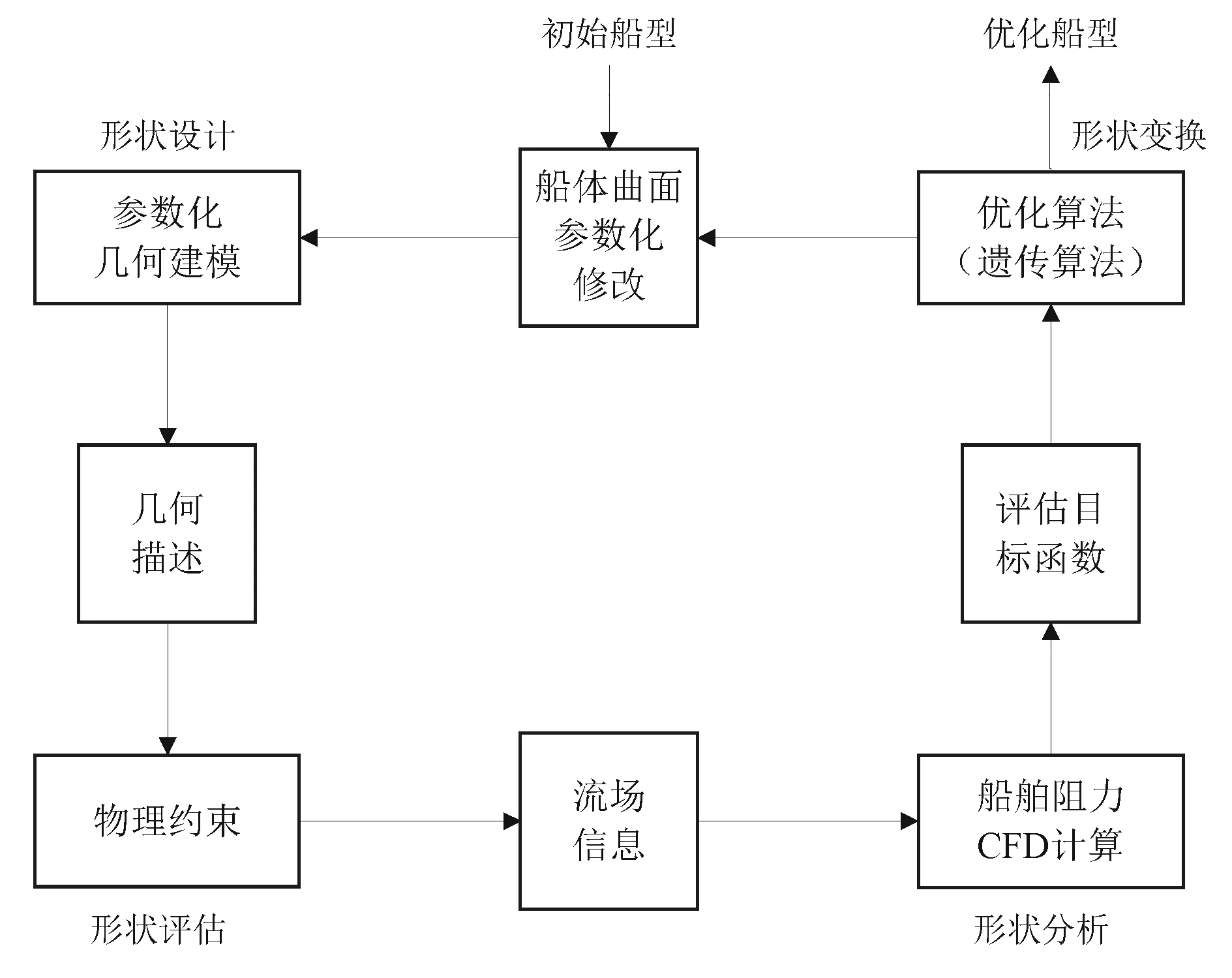
图3 基于CFD的船体型线优化平台

3 国际标模KCS艏部型线优化

3.1 优化问题的描述

对韩国船舶与海洋工程研究所(KRISO)的集装箱船KCS进行艏部线型精细优化研究，优化过程中保持排水量及浮心纵向位置在一定范围内变化。其三维模型如图4所示，主要船型参数见表1。

图4 KCS三维模型

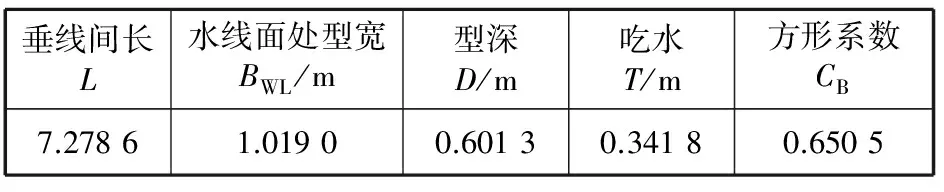
表1 KCS船模主要船型要素

3.2 优化数学模型的建立

3.2.1 优化目标

本文研究的重点是希望优化的船型能够在一定的速度下实现降阻效果，因此，本例的优化目标定义如下：

minfobj=Cw,Fr=0.258

式中：fobj为目标函数；Cw为兴波阻力系数；Fr为傅氏数。

3.2.2 优化变量

艏部控制顶点的选取如图5所示。图中，在船艏部分选择19个可变控制点，其中控制点1和2变化方向为X(船长方向)、Z(吃水方向)，其他控制顶点变化方向为Y方向(船宽方向)。控制点变化范围见表2，这些控制点将作为优化过程中的变量。为保证加工制造的可行性，再选择船底中纵剖面、船艏左端、甲板首尾两端的网格控制点坐标作为优化过程中的不变点，如图5中的粗线表示。

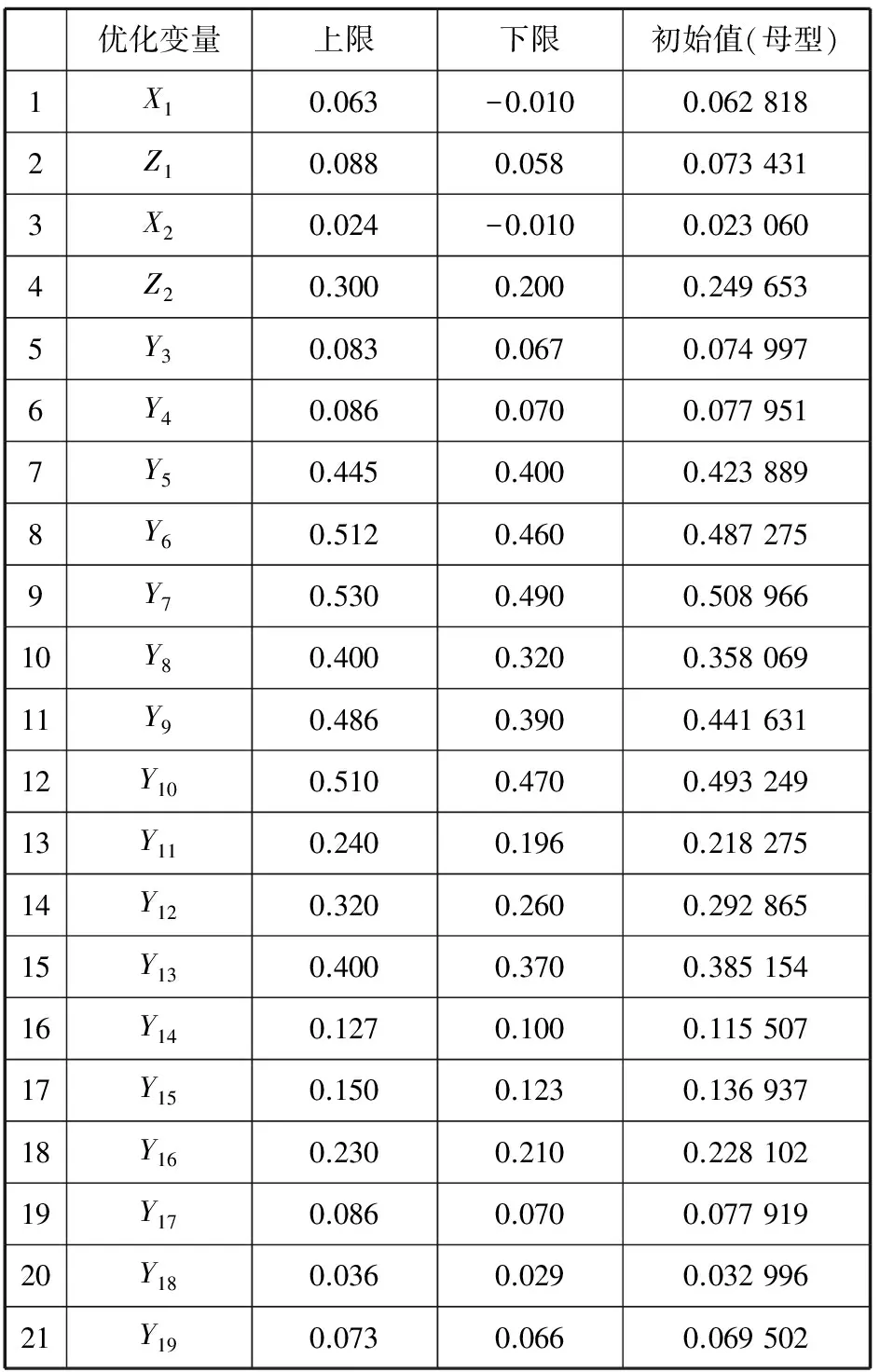
表2 优化变量及取值范围

图5 艏部控制顶点的选取

3.2.3 约束条件

(3)仅改变船艏部线型的几何形状。船宽B、吃水T均保持不变，艉部线型不变。

式中：Δ、Lcb分别为母型的排水量、浮心距舯纵向距离；Δopti、Lcbopti分别为优化船的排水量、浮心距舯纵向距离。

3.3 船型优化流程

船型优化的流程如图6所示。

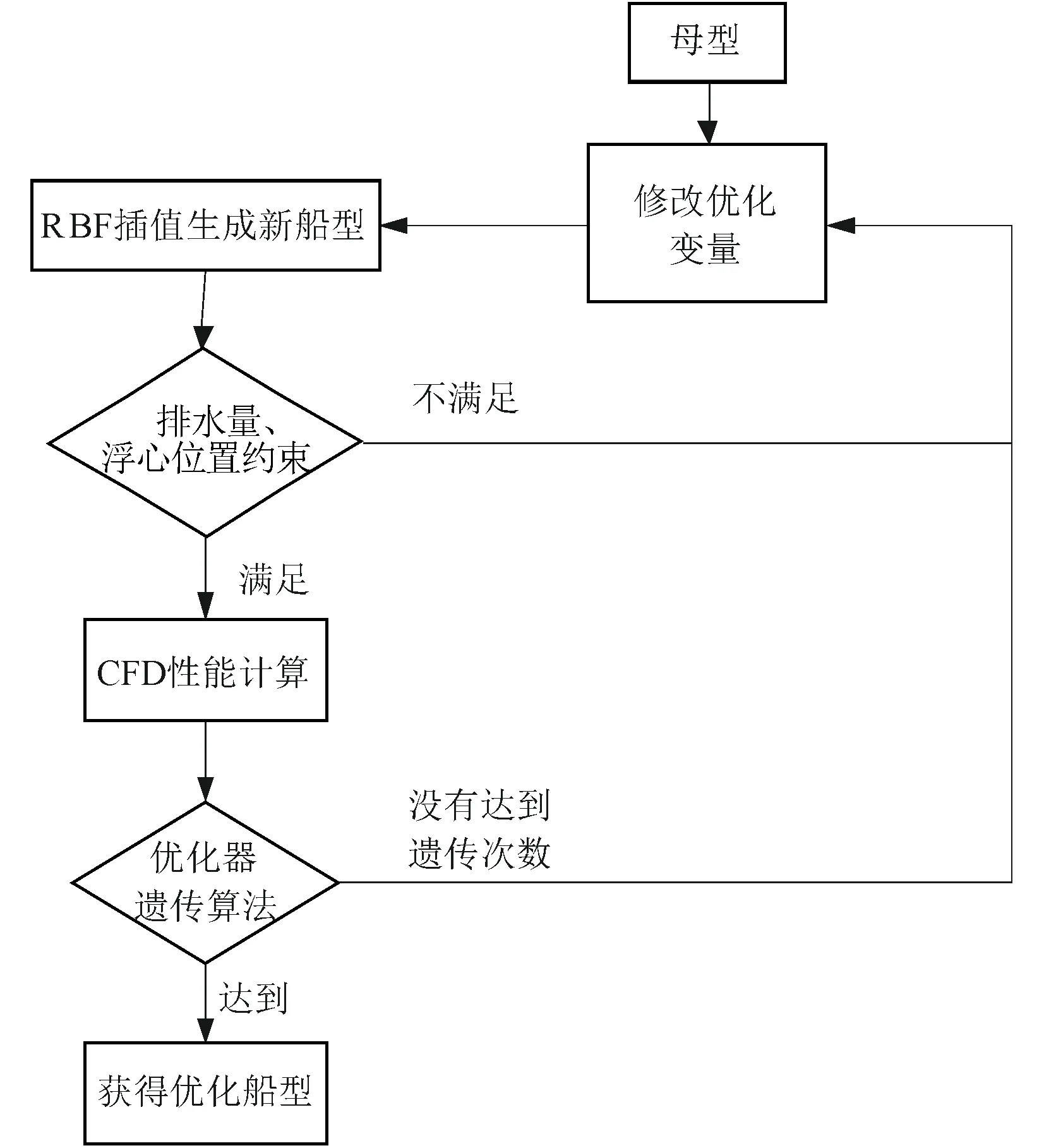
图6 船型优化流程

船型优化流程具体阐述如下。

(1)利用本文第1.2节RBF插值技术进行船艏部曲面的变形。

(2)对生成的每一个新船型进行静水力计算，计算其排水量、浮心纵向位置及湿表面积。若满足约束条件，则通过CFD软件(shipflow)计算船舶兴波阻力；反之，修改优化变量，重新生成新船型。

(3)采用非支配排序遗传算法(NSGA-Ⅱ)进行船型优化。若达到遗传次数则输出优化的船型；反之，修改优化变量，重复上述过程。

3.4 优化结果分析

经过约29h的计算得到优化船型。

3.4.1 优化变量的收敛趋势分析

部分优化变量及兴波阻力系数Cw的收敛曲线如图7所示。优化前后性能指标及约束条件对比见表3。

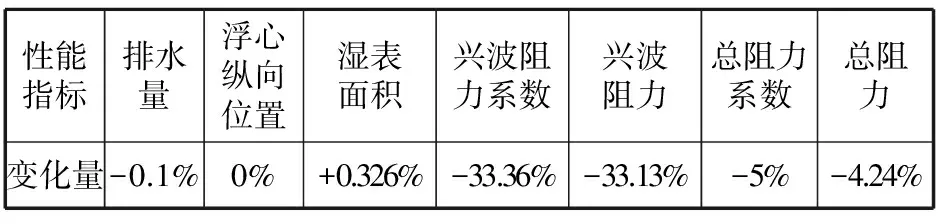
表3 优化前后各性能指标的变化情况

从图7中看出，随着迭代次数的增加，各变量均收敛到最优值。其中，X1、Z1、X2、Y3随着迭代进行逐渐减小，而Z3、Y4随着迭代次数增加也随之增大。

从表3中可以看出，在满足排水量和浮心纵向位置的约束条件下，优化船型比母型的湿表面积稍有增大，兴波阻力系数减少约33.4%，兴波阻力减少约33%。为验证总阻力的降阻效果，对最优船型采用shipflow软件进行了总阻力的数值计算。经计算，优化后总阻力降低约4%，减阻效果明显。

图7 优化变量收敛趋势图

3.4.2 优化前后波形比较

优化前后波形图如图8所示。Y/L=0.079处舷侧纵切波高比较如图9所示，图中，X为流场计算域纵向位置坐标，Y为流场域横向位置坐标。

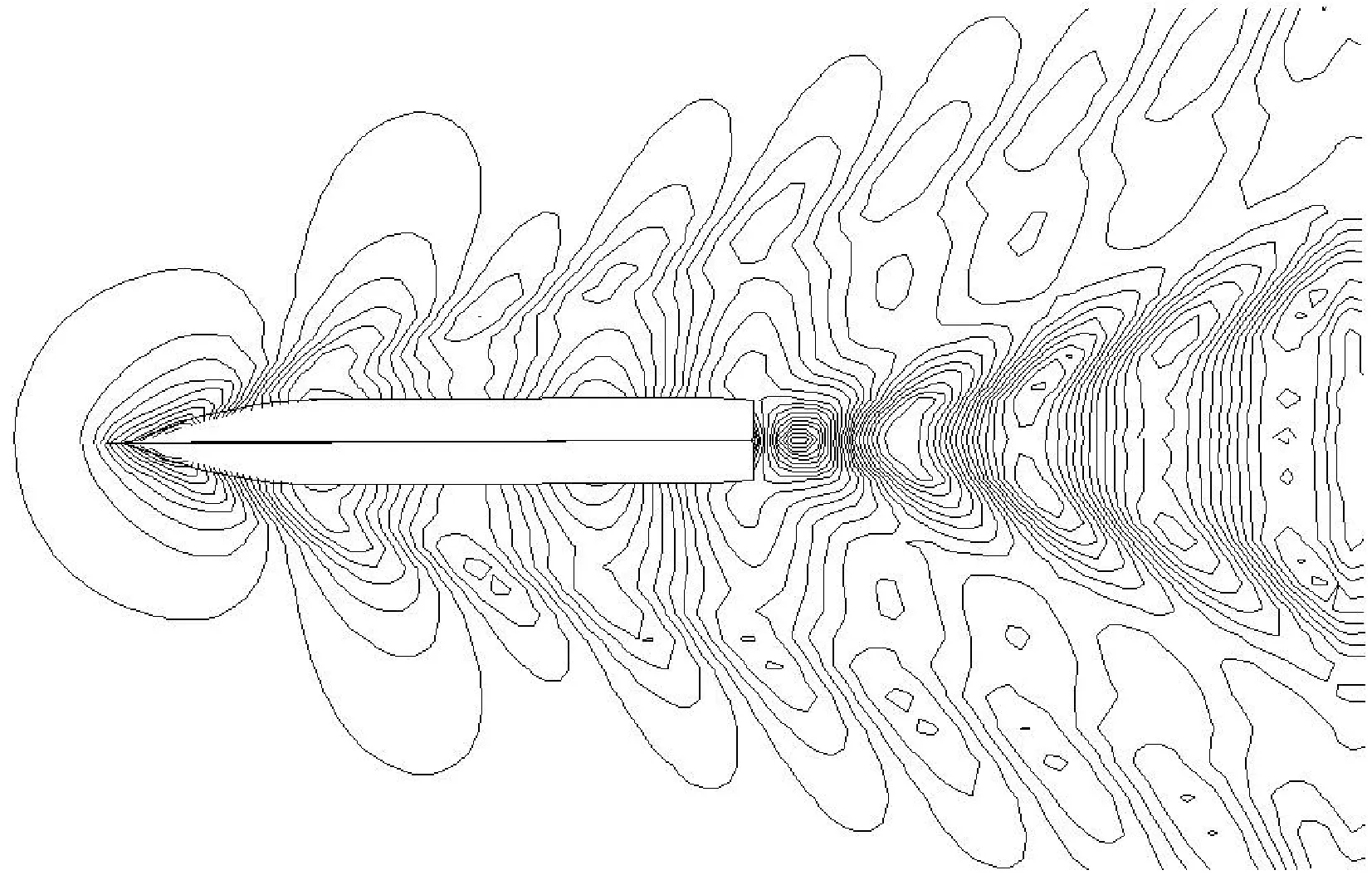
图8 优化前后波形图比较(优化船：上，母型船：下)

图9 Y/L=0.079处舷侧纵切波高图比较

从图8、图9中可以看出，优化后的波形数相对变少，在船艏附近的波形切片幅值也相应减小。

3.4.3 优化前后线型比较

优化后获得的最优方案见表4。横剖线、纵剖线图比较分别如图10、图11所示。

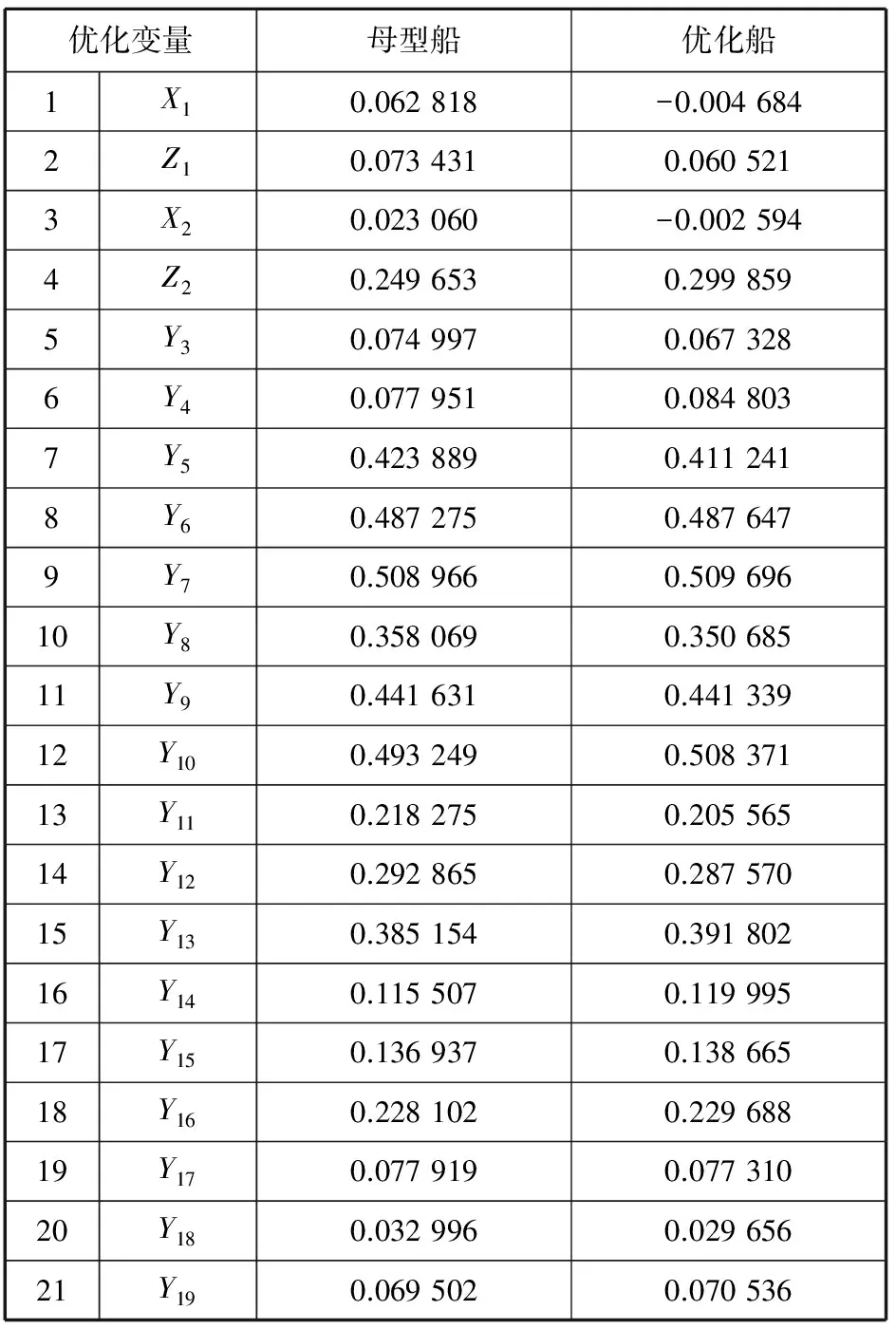
表4 最优方案的取值

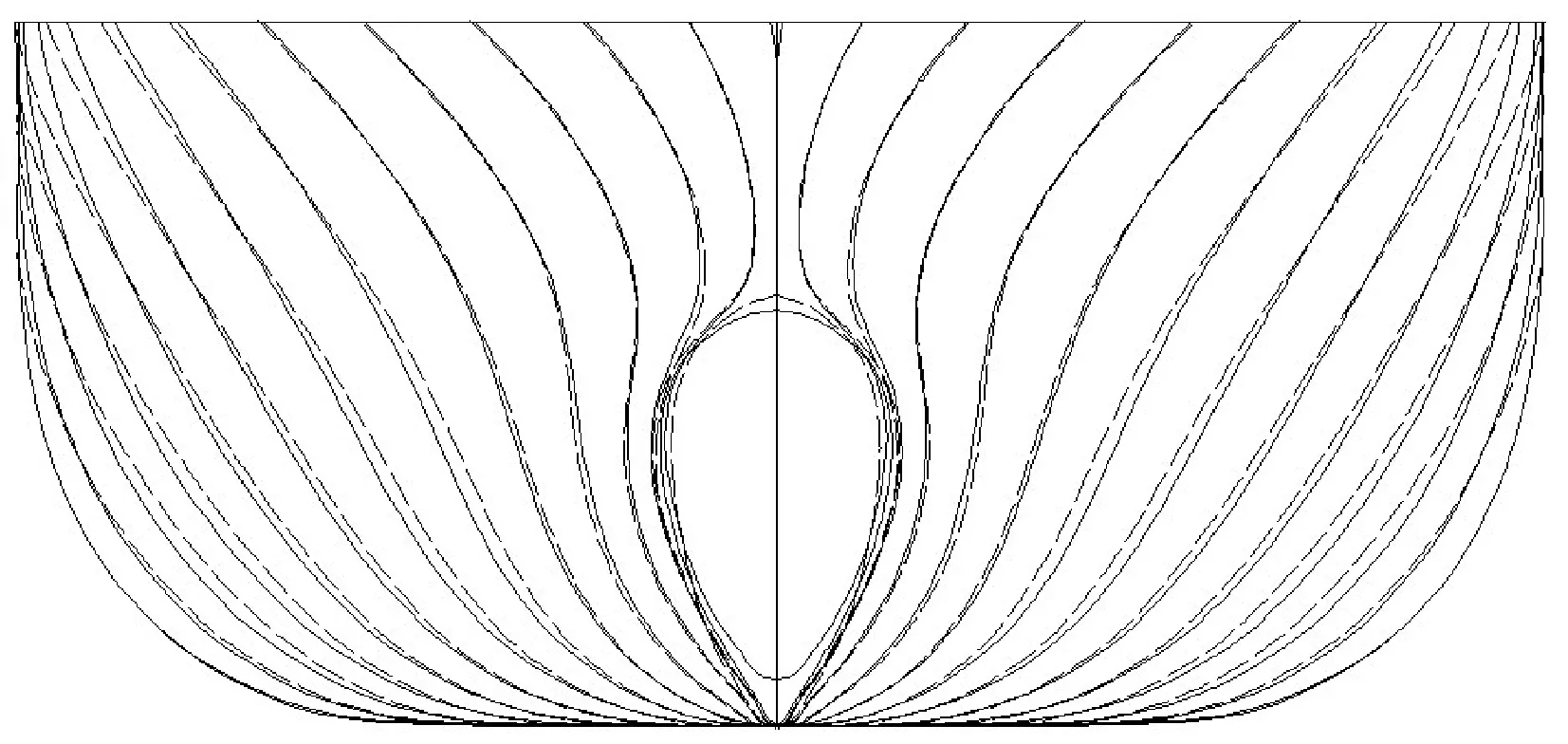
图10 横剖线图比较(实线：母型，虚线：优化)

图11 纵剖线图比较(实线：母型，虚线：优化)

由表4可以看出，变量1～6优化前后的变化较大，说明这6个变量对兴波阻力有很大的影响，而这6个变量正好位于船舶的球鼻艏部位。图10、图11靠近球鼻艏部分的型线发生了较明显变化，也正说明了这一点。

4 结论

(1)RBF曲面插值方法不仅保证了曲面的光顺性，而且使局部线型的变形更为灵活，极大拓宽了船型变化的设计空间。

(2)通过CFD的数值计算和优化算法的寻优机制来驱动控制点坐标的变化，较准确地预报出船体型线的变化趋势，实现了船体型线的仿真优化设计。

(3)船体型线优化平台可满足船舶初期型线设计的需要，具有一定的工程应用价值。

未来的研究主要集中在以下3方面。

(1)目前船艏部的可变控制点在船体表面均匀布置，必然有部分控制点对水动力性能的影响较小。因此，后期拟进一步对这些控制点按照部位进行敏感度分析，保留对优化结果影响较大的点，既节省优化时间又为后期其他船模选择合适的控制点提供经验和依据。

(2)目前船型优化耗费的时间较长，后期将重点针对近似技术开展研究，通过建立近似模型以代替高精度的CFD计算，从而大大节省优化时间。

(3)船舶多学科多目标综合优化是未来的一个发展趋势，因此，后期也将重点开展船舶的快速性、操纵性、耐波性的综合优化研究。

[1] Peri D, Campana E F. Multidisciplinary design optimzation of a naval combatant[J]. Journal of Ship Research,2003,47(1):1-12.

[2] Peri D, Campana E F . High-fidelity models and multi-objective global optimization algorithms in simulation-based design[J]. Journal of Ship Research,2005,49(3):159-175.

[3] Yusuke Tahara, Stern F, Himeno Y. Computational Fluid Dynamics-Based Optimization of a Surface Combatant[J].Journal of Ship Research,2004,48(4):273-287.

[4] 冯佰威，刘祖源，詹成胜.基于船型修改融合方法的参数化建模技术[J].计算机辅助工程,2010,19(4):3-7.

[5] 李胜忠, 赵峰. 基于 BezierPatch 几何重构技术的船舶球艏构型优化设计研究 [C]//吴有生，刘桦，程文，等.第二十三届全国水动力学研讨会暨第十届全国水动力学学术会议文集. 北京：海洋出版社，2011.

[6] 李胜忠.基于SBD技术的船舶水动力构型优化设计研究[D].无锡：中国船舶科学研究中心,2012.

[7] 吴宗敏.径向基函数散乱数据拟合与无网格偏位方程数值解[J].工程数学学报，2002,19(2):10-1l.

[8] Buhmann M D. A New Class of Radial Basis Functions with Compact Support[J]. Mathematics of Computation, 2000，70:307-318.

[9] 沈通，冯佰威.基于径向基函数插值的船体曲面修改方法研究[J]. 中国造船，2013,54(4):45-54.

[10] 周昊,冯佰威,沈通. 基于RBF的船体曲面变形方法及在船体型线优化中的应用[J]. 船舶工程，2014,36(5)：103-106.

[11] Morris A M, Allen C B， Rendall T C S. CFD Based Optimization of a Aerofoils using Radial Basis Functions for Domain Element Parameterization and Mesh Deformation[J]. International Journal for Numerical Methods in Fluids, 2008，58: 827-860.

2016-05-06

国家自然科学基金资助项目(51279147；51179143；51479150；L1422029)

冯佰威(1974—)，男，副教授，主要从事计算机辅助船舶设计、船舶多学科设计优化技术研究；叶诗瑶(1993—)，女， 硕士研究生，主要从事船舶多学科设计优化技术研究；常海超(1985—)，男，博士研究生，主要从事船舶多学科设计优化技术研究。

661.31

A