九年级《圆》“知识树”设计的策略研究
赵琳娜
[摘要]新时期的九年级数学教学中,根据素质教育的需要,为实现高效课堂的构建,势必要提高教师的处理及驾驭教材的能力,结合以往的教学实践来看,设计“知识树”并根据其实施对教材的讲解效果显著.根据此,本文将以九年级《圆》“知识树”设计及应用为例,对“知识树”在当前中学教学中的应用进行积极探讨,
[关键词]“知识树”;圆;设计;策略
当前九年制义务教学发展中,构建高效课堂在教师驾驭教材的水平和处理教材的能力的有效提高方面极其重要,而在其对应的实现途径方面,绘制“知识树”无疑是一项非常实用的措施,构建设计“知识树”并将其运用于实际教学,不但能教会学生对知识的梳理、归纳和总结,更有利于教师把握教材,实现教学的高效性,从而让学生达到对相关知识整体构建和系统化掌握,加深了对教学大纲的理解,奠定了高效课堂实施的标准,对于学生的更高效、更有针对性学习意义重大
“知识树”的绘制要求 .新时期教学发展中,中学教学对于“知识树”的设计和运用,应当分以下几个步骤来完成:首先确定单元教学目标,继而整合分析本单元内容在学段知识体系中的位置,及时明确将学段知识体系中本单元教材内容所处的作用及地位,并结合对学生已积累的经验的分析,按照课标对本单元的教学目标进行确定;其次,是要抓住教材的“点”和“眼”进行“知识树”的设计和解说,具体实施中,绘制并解说本单元知识的重难点及高频考点等,继而对相关解题策略进行分解,利于教学难点和关键点的突破,确保课堂实现高效,使得运用“知识树”教学恰到好处;最后是知识的整合思想及策略,结合学生的已有经验及教师对教材知识结构的理解,对教学内容进行合理调整、补充和取舍,促进学生的更高效学习,实现对教学资源的合理挖掘和使用,这对于学生的发展意义重大,后续结合对单元达标练习题的筛选与设置,方能达到教学的最终目标,促进学生对该单元知识的学习,
设定教学目标
在新时期的九年级数学教学中,运用“知识树”学习“圆”这一知识点,首先要设定教学目标,结合圆的相关教学实践来看,知道圆是轴对称图形,了解圆和圆的相关概念是其最基础的教学目标,需在此基础上对垂直于弦的直径有哪些性质进行理解和掌握,明确圆周角、圆心角及弧等的概念及其之间的关系.在学生学习本单元知识后需要解决的问题方面,需要学生结合对垂直于弦的直径的性质进行掌握的基础上,能解决一些简单的实际问题,数学源于生活又高于生活,在运用圆的相关性质解决实际问题时,促使学生逐渐形成实事求是和勇于创新的精神,利于其后续的全面发展,
教学的重难点分析
综合九年级数学教材中圆这一单元的具体内容来看,垂径、圆周角定理及其推论无疑是其教学的重点,具体而言,垂径定理及其推论是对圆重要性质的反映,是证明线段相等、垂直关系及角相等的必要依据,更是对圆的轴对称性的具体化,是进行圆计算与作图的重要依据及方法另外,在角相等、弦相等等问题的解决方面,圆周角定理及其推论的作用较大,其构成了圆“知识树”教学的重点.此外,结合笔者多年的教学经验来看,圆周角定理的证明及垂径定理及其推论无疑是圆相关内容学习的难点,基于其结构复杂及易混淆等原因,使得垂径定理及其推论变得困难,而完全归纳法则是圆周角定理的证明方法,学生不易理解和运用,这也使其成为次单元教学的难点.
圆“知识树”设计与教学步骤
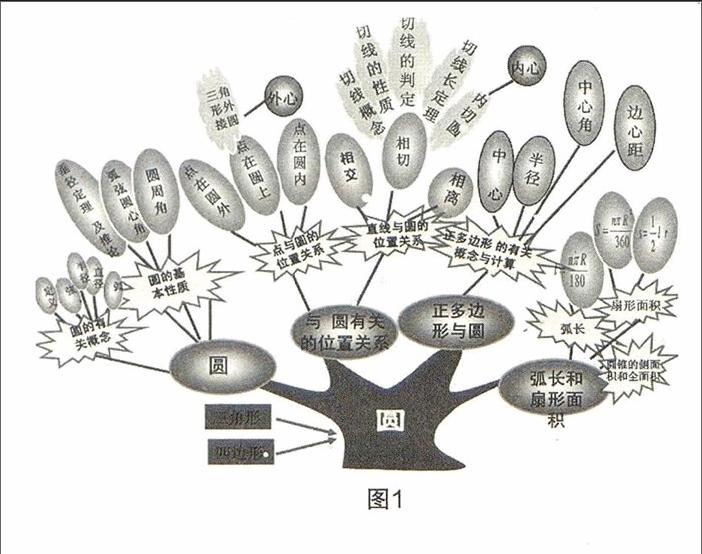
结合圆的相关知识及教学大纲的要求,笔者设计的九年级圆教学的“知识树”如图l所示,结合四边形与三角形等教学基础,引出圆的教学内容,继而将其分为四大模块:圆的定义及概念、与其有关的位置关系、其与正多边形的关系、弧长和扇形面积的计算.每一个模块又分为若干内容,共同构成了圆的“知识树”.下面,我们将对其教学的具体实施进行探讨
1.设计情景,引入新课
在具体的教学中,将准备的日常圆形物品向学生进行展示,这种和谐、美丽的图形,学生在小学阶段已有接触,且能简单计算出圆的周长和面积.在设计情景和新课引入时,结合战国时期对“圆”的记载,引入古语中的“圆,一中同长也”,继而定义圆,使学生知道圆上各点到圆心的距离都等于半径,形成对圆的初步理解.然后教师引入思考:现实生活中为什么车轮会做成圆形的,而非四边形或是三角形?等等,带着这种疑问,引领学生开始对圆“知识树”的学习.
2.引入和总结概念,探索新知识点
此环节教学中,将圆的学习分为四个模块,分别为圆的概念、与其相关的位置关系、其与正多边形的关系、弧长和扇形面积的计算.具体教学中,利用多媒体,播放多种圆物质的图片,结合对图片的观察,让学生去讨论、交流,描述出什么图形是圆,由教师在此基础上总结出圆的定义;在对圆的表示方法方面,一般用“⊙0”表示以点O为圆心的圆,将其读作“圆O”;接着则是要教会学生画圆,在学习与圆有关的概念方面的知识时,让学生明白圆的直径即为经过圆心的弦,弦即为连接圆上任意两点的线段,而对应的优弧则为大于半圆的弧,劣弧为小于半圆的弧.
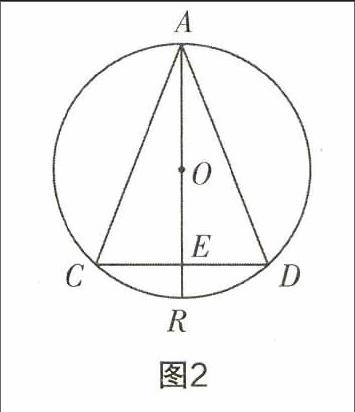
在与圆有关位置关系模块的学习中,用纸剪出一个圆,接下来沿任意一条直径数次对折,让学生总结出其中的结论,使其在积极探讨的过程中,认识到圆有无数多条对称轴;接着要带领学生去探究垂径定理,具体实施中,我们做一个圆,如图2,标出其中的一条弦为CD,接下来沿其垂直方向作一条直径AR,设点E为其垂足,提出两个问题:(1)圆是轴对称图形吗?若是,找出其对称轴;(2)图中有哪些相等的线段和弧?借助于这种探索方式,让学生们通过对圆“知识树”的学习,探索出对称性及垂径定理,利用等腰三角形的构造,将直径看作圆的对称轴,我们即可得出平分弧的结论.以此类推,探讨正多边形与圆的关系,然后推导出弧长的计算公式、扇形面积的计算公式等.
例:赵州桥是我国隋代建造的石拱桥,已有1300多年的历史,它的主桥是圆弧形,弧所对的弦的长也就是跨度是37.4m,弧的中点到弦的距离也就是拱高是7.2m,同学们可以尝试着计算出赵州桥主桥拱的半径.
3.解决典型例题,体验新知识的运用
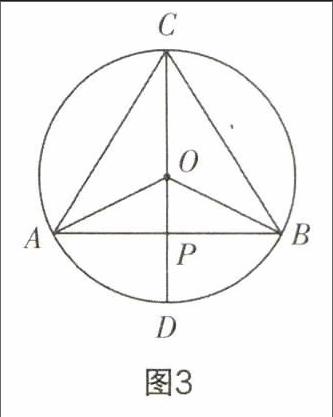
在结合设计的圆的“知识树”进行教学的过程中,教师应当完善对典型例题的运用,借助其进行相关知识的深入学习.让学生深化对某个知识点的学习,如图3,在⊙o中,弧AB与弧AC相等,且∠ACB=60°,求证:∠AOB=∠BOC=∠AOC.这些知识的运用,对于新的知识点的强化i己忆及实践运用作用重大
4.总结、评价教学,分享收获
此环节,应当使学生在运用圆的“知识树”进行对圆的相关内容学习的基础上交流及体会,并及时总结出自己所学的知识.如有学生这样总结:一是对圆有关概念的学习掌握;二是对弧、弦、圆心角的相关性质的理解;三是证明得出垂径定理及其逆定理;四是对圆周角的概念及相关性质的理解学习.这种学习方式有助于学生更好强化对圆相关知识的学习.
5.结合教学内容,布置课后作业
拓展延伸一直是我们进行九年级数学教学的重要方式,而布置作业则是实施这一方式的表现,利于学生对所学知识融会贯通,深入了解,加深他们的记忆,如可以布置以下题目进行后续强化学习,
例1:如图4,在⊙0上有三点A,B,C,其中∠AOC=100°,求∠ABC的度数为( )
A.120°
B.140°
C.130°
D.110°
结束语
在新时期发展的大背景下,新课标的改革使得义务教育阶段越来越注重课堂效率的提高,在本文的写作中,笔者结合自身的教学经验,对九年级数学教学中圆相关知识的“知识树”方式教学进行了积极探究,从设计到具体教学步骤的展开,仔细分析了其教学过程,以期能为新时期的九年级数学教学的实施提供有益的参考.endprint

