船模Z形操纵运动数值模拟与分析*
向 国 欧勇鹏 吴 浩
(海军工程大学舰船工程系 武汉 430033)
船模Z形操纵运动数值模拟与分析*
向国欧勇鹏吴浩
(海军工程大学舰船工程系武汉430033)
摘要:为了研究船舶操纵运动过程中螺旋桨与舵的水动力变化规律,基于URANS方程,联合采用体积力法、重叠网格技术、6-DOF运动模型、VOF模型,计及船体航行姿态的影响,开展了双桨双舵双尾鳍水面船舶的Z形运动数值模拟,通过计算所得横倾、纵倾、超越角、初转期等与试验结果的对比,验证了数值方法的可靠性.在此基础上,分析并获得了双桨船在Z形操纵运动过程中螺旋桨推力与转矩及舵力与转矩的时历变化规律.
关键词:体积力法;Z形运动;数值模拟;重叠网格;舵力;螺旋桨推力
向国(1990- ):男,硕士生,主要研究领域为舰船水动力性能
*水动力学重点基金项目资助(批准号:9140A14030712JB11044)
0引言
获得船舶操纵过程中船体运动与螺旋桨及舵的水动力同步数对深入分析并改善船舶的操纵性具有重要意义,是船舶科研工作者长期以来所关注的科学问题.然而,通过自航模试验获得操纵运动过程中的舵力,以及螺旋桨推力转矩,不仅对试验环境与测试仪器要求高,而且试验方法尚不成熟[1].
采用数值计算的方法,直接数值模拟水面船舶Z形自航试验,不仅可获得操纵运动的基本参数,还可分析螺旋桨旋转、转舵过程中的流动细节,揭示船舶操纵运动过程中的船体运动与螺旋桨、舵的水动力相互关系.目前,Pablo M. Carrica等[2-4]采用自主开发的软件CFDShip-Iowa,在超大型计算服务器上直接模拟船舶在静水以及在波浪中的操纵运动,同时运用体积力法来代替螺旋桨旋转初步探索了水面舰艇MARIN-7967的回转以及Z形试验,但所得结果尚存在较大误差.G.Ryan等[5]运用体积力法和重叠网格对水下航行器的Z形运动模拟进行了改进,但忽略了横倾、纵倾的影响,所得结果具有一定的局限性.
本文在RANS方程及k-ε湍流模型的基础上,联合采用重叠网格技术、6-DOF运动模型、VOF气液两相流模型,构建了双桨双舵船模的Z形试验数值计算方法,并通过了模型试验验证,在此基础上,分析并获得了Z形操纵运动过程中螺旋桨推力转矩及舵力的变化规律.
1数值模拟方法
数值计算基于非定常RANS方程,其控制方程,螺旋桨模型,船体参数以及计算域与网格具体如下.
1.1控制方程
在空间固定坐标系下,不可压缩流体雷诺平均的连续性方程和动量方程为
(1)
(2)
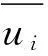
由于2个方程不封闭,所以需要湍流模型对雷诺应力项进行处理,选用k-ε模型,控制方程如下
(3)
(4)
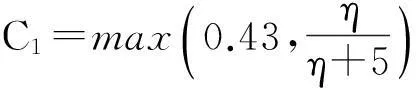
1.2螺旋桨模型
采用体积力法来等效螺旋桨的推力和转矩,忽略螺旋桨叶片几何形状的影响,将推力按半径变化分布在由桨盘面直径、螺旋桨纵向厚度所定义的圆柱形区域内,力的分布采用Goldstein优化方式,其数学表达形式如下.
(5)
(6)
式中:fbx为轴向力;fbθ为切向力;
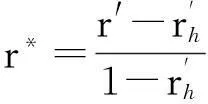
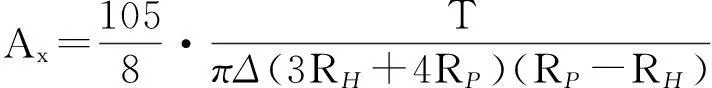

其中:RP为螺旋桨半径;RH为桨毂半径;r为辐射半径;T,Q分别为敞水螺旋桨的推力和转矩.
本文船模螺旋桨为一对内旋桨,单桨的敞水性能曲线见图1,采用如式(9)所示的6次多项式进行拟合,所得系数见表1.
Y=a+bx+cx2+dx3+ex4+fx5+gx6(7)

图1 螺旋桨的敞水性能曲线
1.3 几何模型及坐标系
模型为双桨双舵双尾鳍船,基本参数见表2,船体见图2.
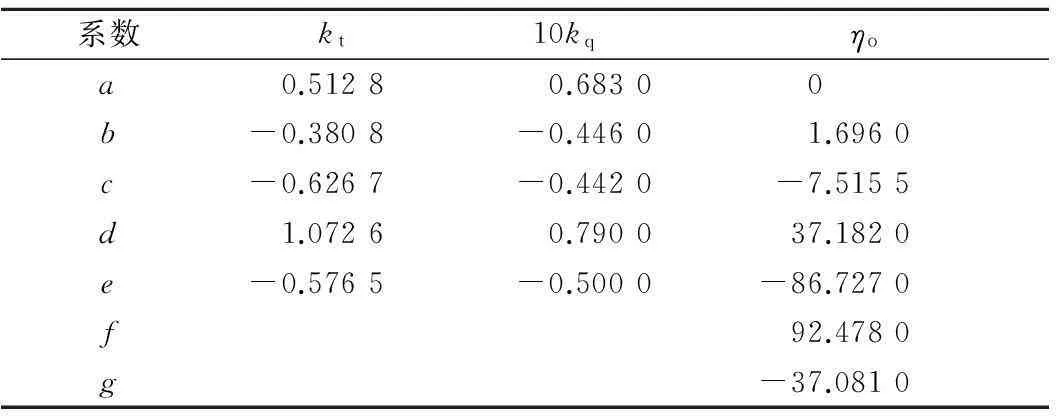
表1 螺旋桨敞水曲线多项式系数
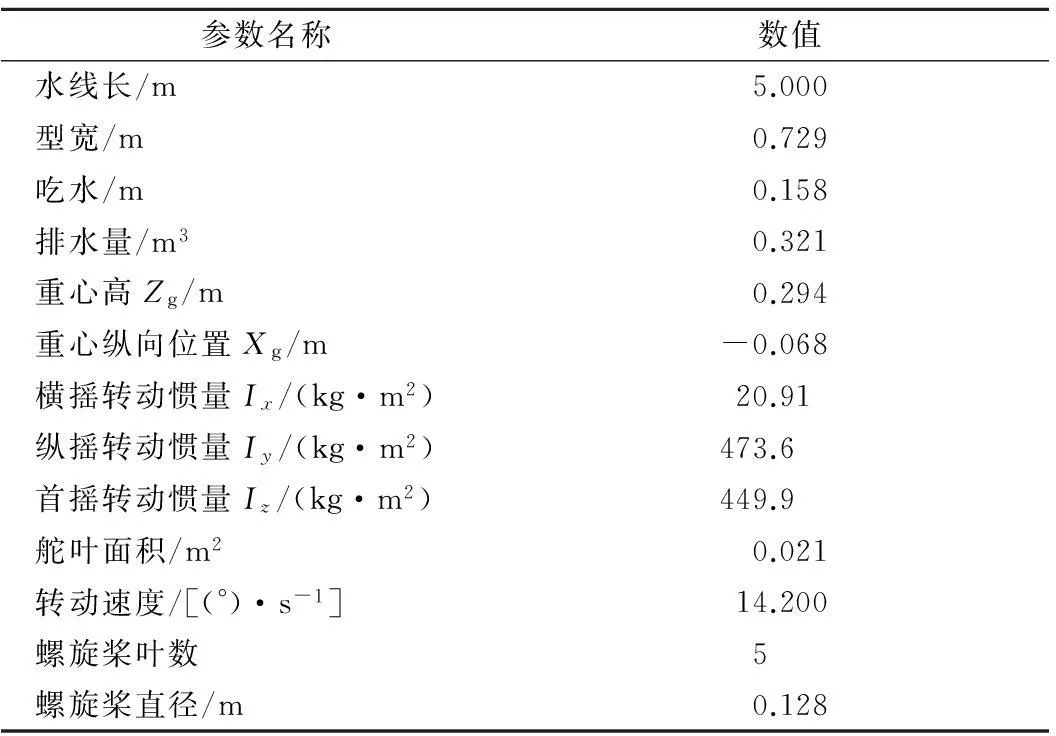
表2 模型的基本参数

图2船体模型
1.4计算域与网格
计算流域共3个,其中1个为船体流域,2个为舵的流域,见图3~4.船体流域为等腰梯形区域,可更好地适应Z形运动过程中的流场特征(见图3),并降低网格数量.流域总长为4倍船长,前方距离船首1L(L为船长),宽为0.5L,设置为速度入口;流域后方距离船尾为1.5L,宽为3.5L,设置为压力出口;流域左右侧面与前方入口的夹角为53°,设置为速度入口.流域总高为0.9L,上表面距离船底0.2L,下表面距离船底0.7L,均设置为速度入口.
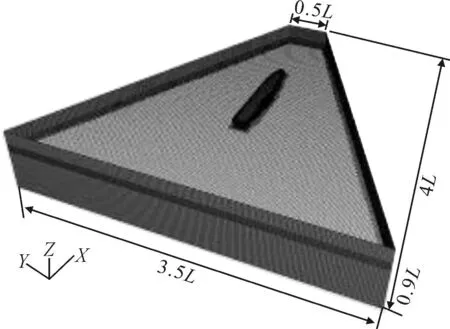
图3 船体计算域
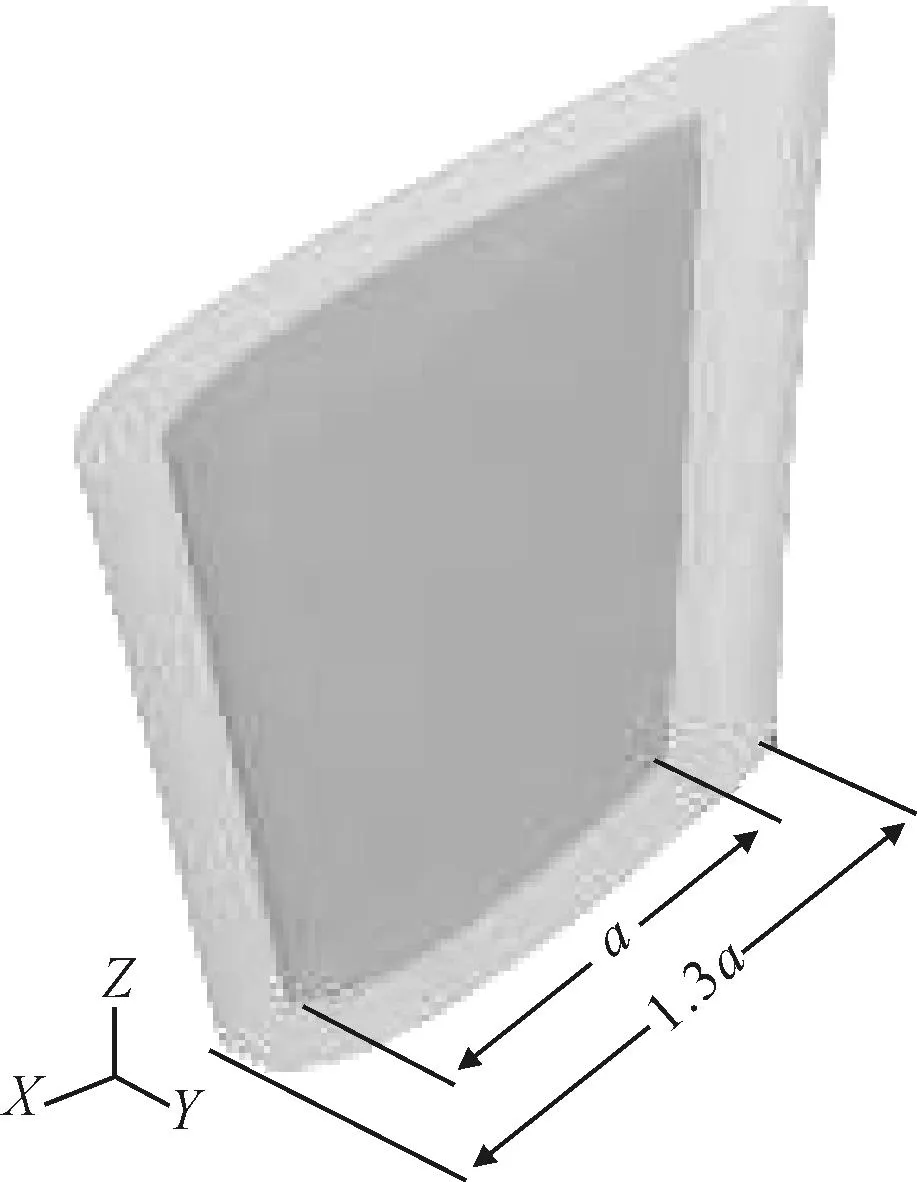
图4 舵流域
计算域采用全六面体剪切型网格(trim网格)进行离散,共202万,其中船体流域180万,舵流域各11万.为保证网格布局合理,对船体、舵、桨、自由液面等区域进行了网格加密.
2数值模拟结果与分析
2.1自由直航
表3给出了船模自由直航时航速的模拟结果与试验值的对比,由表3可见,数值模拟所得航速值与试验值的偏差小于1%.图5给出了相应的船体兴波图像,从波形上看,数值计算结果与模型试验结果基本一致.
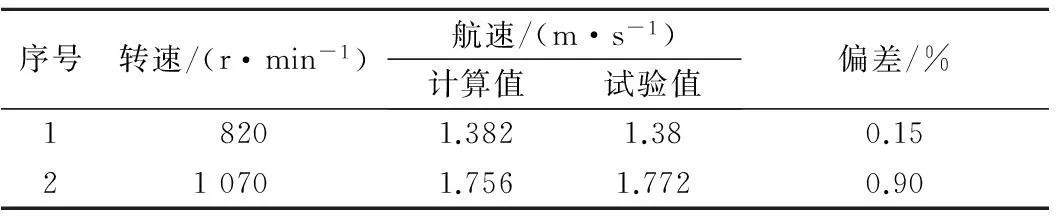
表3 Z形对比的2个状态

图5 直航兴波图像与试验的对比
2.2Z形运动特征参数
数值计算了V=1.38 m/s(Fr=0.195)、舵角10°/10°,20°/20° 2个角度的Z形运动.给出了横摇、纵摇、航向角、航速、轨迹、舵力、螺旋桨推力转矩等参数随时间的变化.
表4为数值模拟结果与试验结果对比,表中:ta为初转期、ts为超越时间、T为周期、ψs1为第一超越角、θmax1为第一次横倾幅值、ψs2为第二超越角、θmax2为第二次横倾幅值.
初转期ta和超越时间ts的绝对误差在0.22~0.35 s之间,相对误差范围为为6.3%~11.3%;周期T的最小误差仅0.6 s;超越角的最大误差为24.0%,但绝对误差仅为1.2°,与试验值基本相符合;最大横倾角的误差范围在0.4°~0.65°.
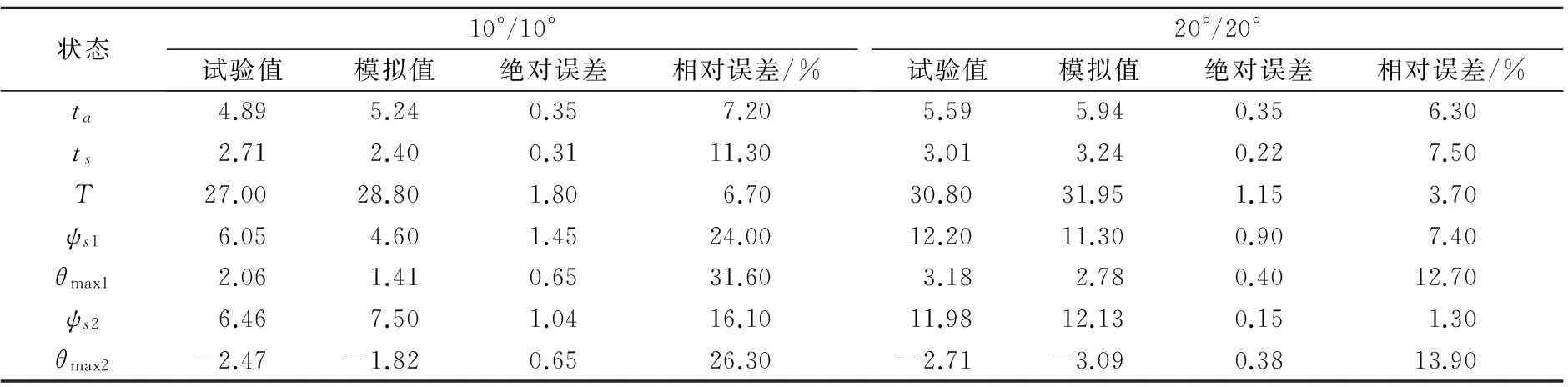
表4 Z形特征参数的结果对比
2.3船体运动时历曲线
图6分别给出了航速V=1.38 m/s,20°/20° Z形运动状态下舵角、航向角、轨迹、航速、横倾、纵倾、的时历曲线.由图6可见,数值计算所得航向角、横倾、纵倾、航速、轨迹的时历曲线与试验结果基本一致.
图7分别给出了模型Z形运动过程中,向左回转与向右回转时的船体兴波图像.由图7可见,数值计算所得波形图与试验结果基本一致.
可见,本文数值计算方法可较好的实现双尾鳍水面舰船操纵运动的模拟,所得运动时历曲线、波形图像均具备较好的精度.
2.4螺旋桨推力
图8给出了20°/20° Z形运动过程中,螺旋桨总推力的时历变化曲线.由图8可见,舵角为零时,船体向前直航,螺旋桨推力趋于一个稳定值;当开始打舵进入Z形运动状态后,螺旋桨总推力呈现周期性变化.
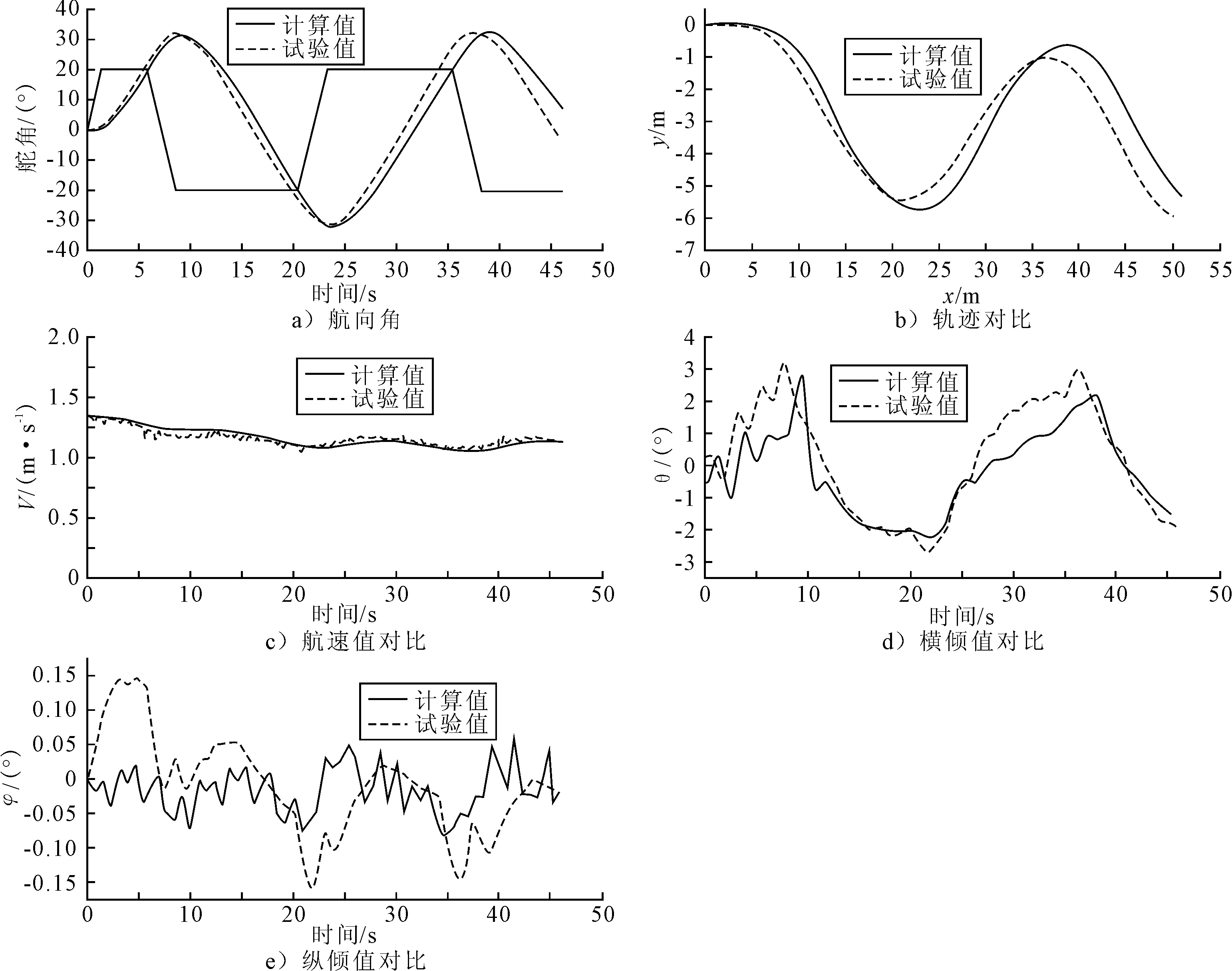
图6 V=1.38 m/s,20°/20° Z形模拟与试验航向角、舵角、轨迹、航速、横倾和纵倾的对比

图7 20°/20°不同时刻的自由面波形
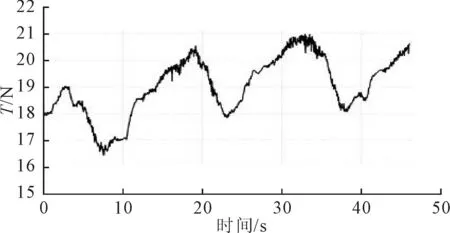
图8 螺旋桨总推力时历曲线
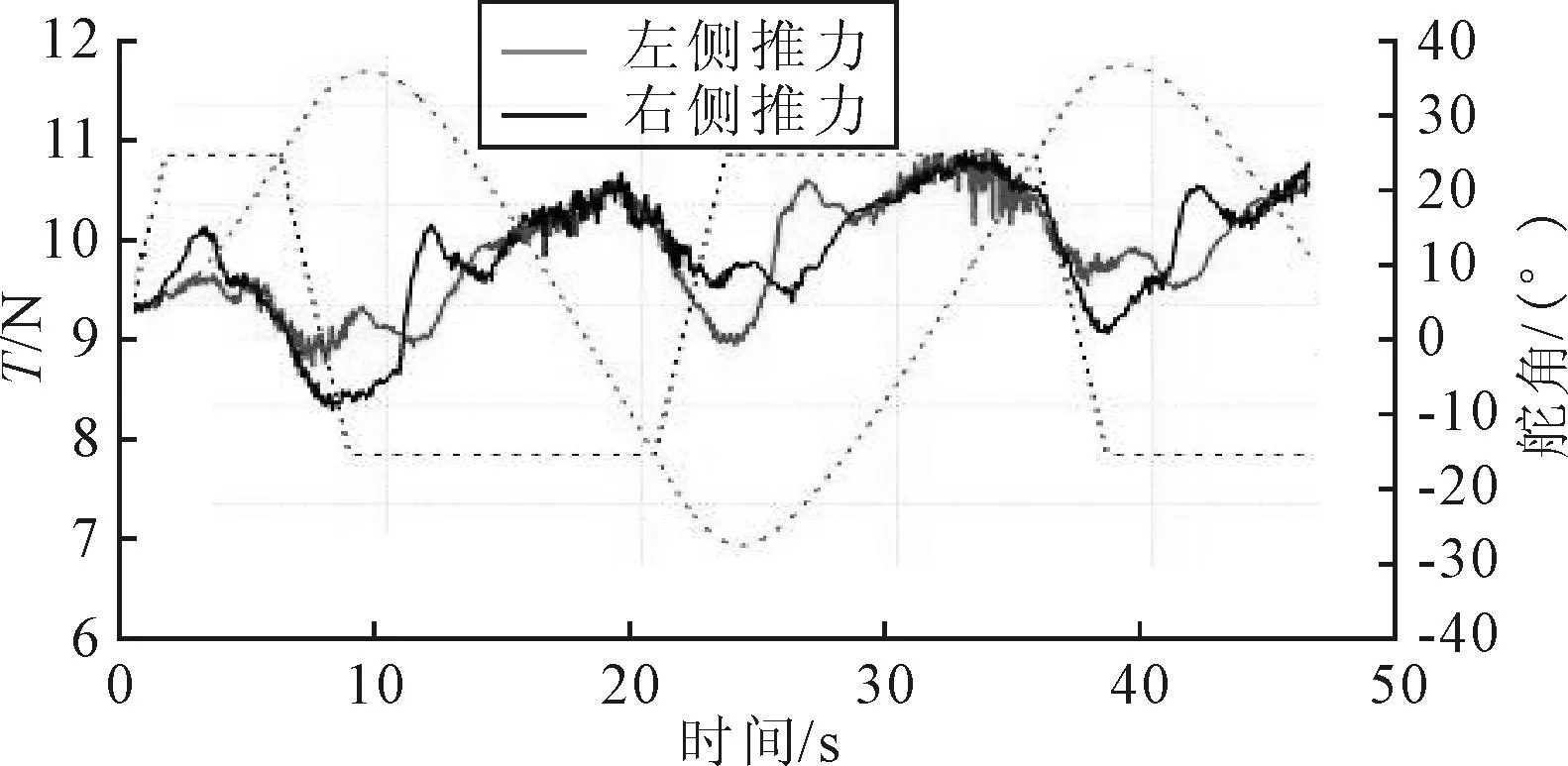
图9 螺旋桨推力时历变化曲线
图9给出了20°/20° Z形运动过程中,螺旋桨推力与舵角、航向角同步变化时历曲线,图中舵角为正表示打右舵.由图9可见,第一次打右舵完成后,左右2桨的推力均先增大,后减小,存在一个明显的峰值,峰值出现在航向角开始明显变大时刻附近(见图10).随后,舵板向右舷移动至指定舵角,每次在舵状态变化时刻附近(开始转或转后停)推力都会出现峰值.
由图9还可以看出,船体向右回转时,右侧螺旋桨推力大于左侧;船体向左回转时,左侧螺旋桨推力大于右侧.这主要是因为转首时,左右螺旋桨盘面处伴流不同引起的,如图11所示为第一次打舵完成后,桨盘面后方0.1D处的轴向速度分布图.
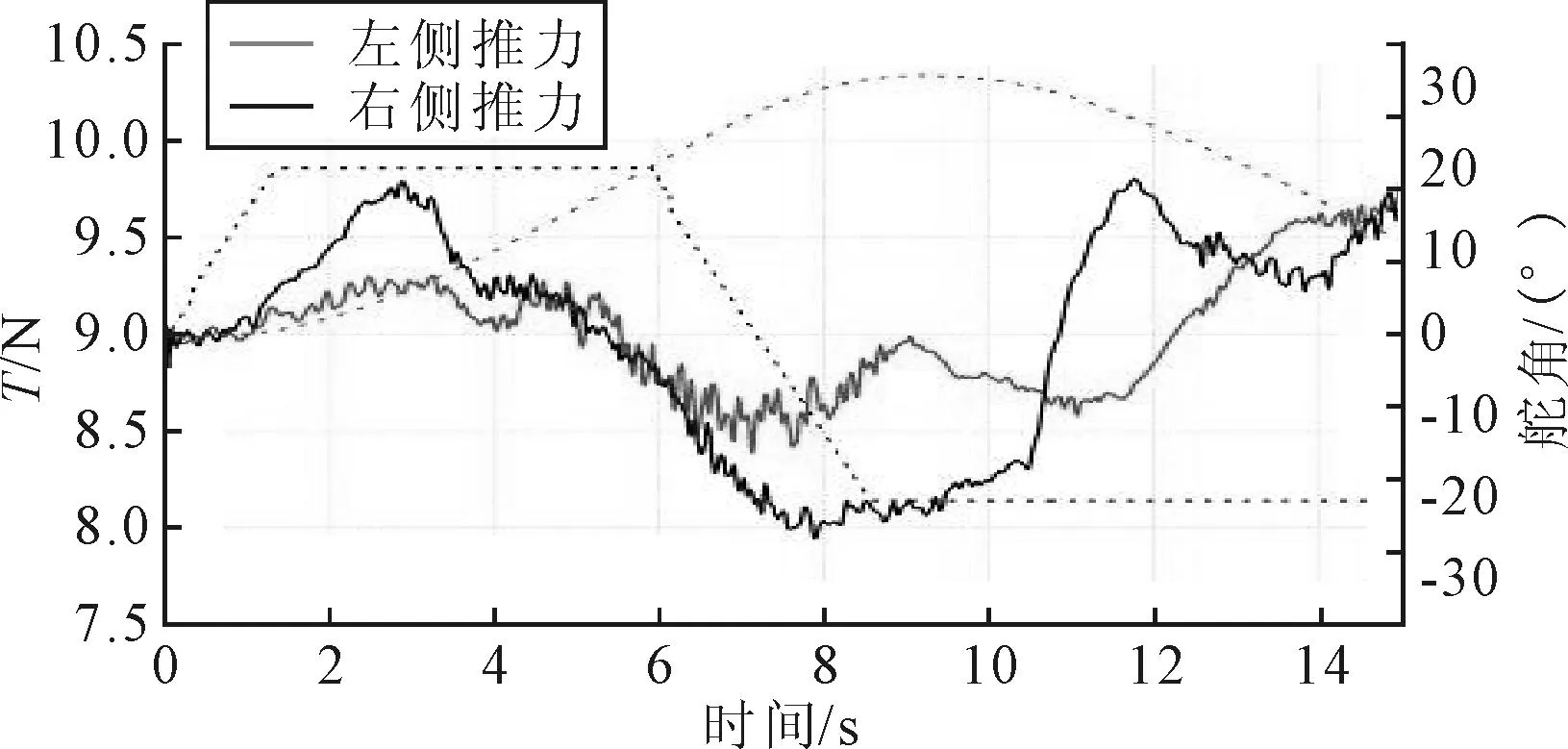
图10 第一个峰值处对应的舵角、首向角曲线局部放大

图11 轴向速度分布图
2.5舵力和转矩
图12给出了20°/20° Z形操纵运动过程中舵升力随时间的变化,图中同时给出了相应的舵角变化曲线.可以看出,舵板从零度舵角向左转舵至20°的过程中,随着舵角增加,舵升力增大,存在一个峰值,此时为舵板运动至最大舵角位置处的时刻.当舵板运动至目标舵角并保持不变,随着船舶发生回转运动,舵板上的升力逐渐降低,直至舵角反向为右舵.此时,舵升力的舵升力方向相反,但其变化规律与打左舵时完全一致.
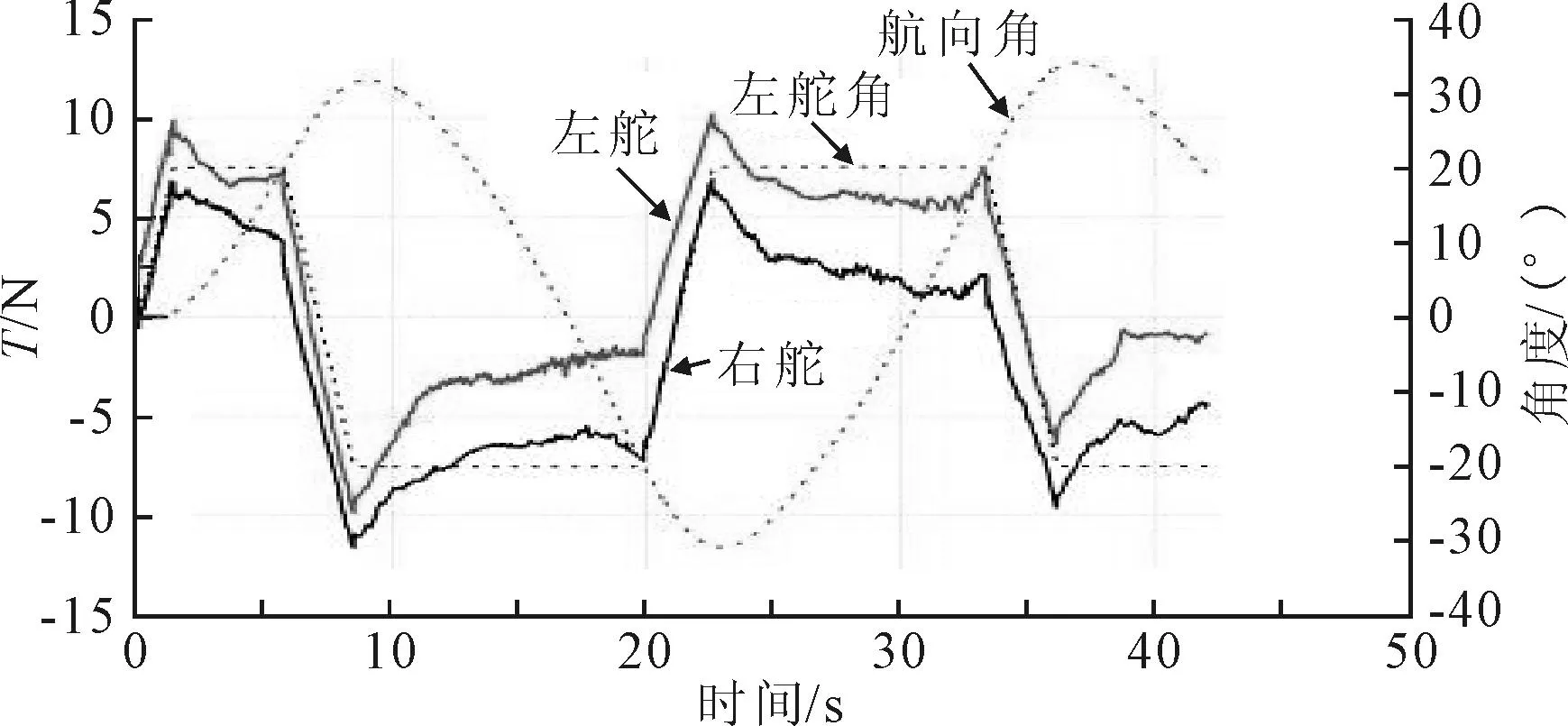
图12 20°/20° Z形运动过程中舵力时历曲线
由图12还可以看出,当打左舵船体向左回转时,左侧舵板上的升力较右侧舵升力大;而打右舵时,右侧舵板上的升力大于左侧.这主要是因为在回转过程中,船体左右流场不对称,使得左右舵板上的压力不一致导致的,见图13.
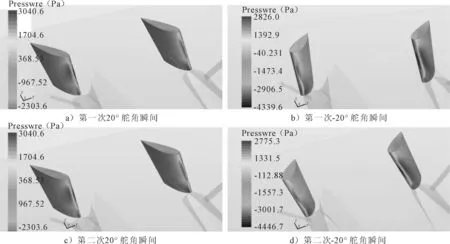
图13 舵附近的压力云图(左边为右舵)
图14给出了Z形运动过程中,舵轴所受水动力转矩随时间的变化曲线.由图14可见,舵板向左转舵过程中,舵转矩随舵角的增加而增大,当舵板转动至20°舵角处时,舵转矩增加至最大值,之后舵转矩逐渐减小.值得注意的是,在舵板转动至目标舵角处时(如图中的t0时刻),舵转矩形成一个“尖锐”的峰值,且在每次舵板开始转动与停止转动时均存在一个转矩峰值(如图中t1、t2、t3时刻),过大的瞬时舵转矩值可能会引起舵机功率不足而出现卡舵现象,在船舶操舵过程中应加强注意.

图14 Z形运动过程中舵转矩时历曲线
由图14还可以看出,回转过程中,左右舵转矩不一致.当打左舵时,左侧舵转矩大于右侧;打右舵时,右侧舵上的转矩大于左侧,两者最大差别可达50%.
上述分析主要以20°/20°例,10°/10°与20°/20°的变化规律一致,仅舵力大小不同,且10°/10°在不打舵状态要平稳,变化范围小.
3结论
1) Z形模拟结果具备一定的精度.
2) 通过对Z形运动过程中船体受力的同步分析,获得了螺旋桨与舵的水动力变化规律.
3) 左右桨的推力大小在Z形转首时呈现周期性交替变化,且内侧桨推力大于外侧.
4) 在Z形运动过程中,每次打舵瞬间,舵升力都会出现一个峰值;左右舵升力内侧舵大于外侧舵;左右舵转矩与舵力的变化规律基本一致.
参 考 文 献
[1]SAHBI K. Manoeuvring characteristics of twin-rudder systems: rudder-hull interaction effect on the manoeuvrability of twin-rudder ships[J]. Journal of Marine Science and Technology,2011(16):472-490.
[2]ALIREZA M, PABLO M C. Simulations of zigzag maneuvers for a container ship with direct moving rudder and propeller[J]. Computers & Fluids,2014,96:191-203.
[3]PABLO M C. Hamid sadat-hosseini CFD analysis of broaching for a model surface combatant with explicit simulation of moving rudders and rotating propellers[J]. Computers & Fluids, 2012,53:117-132.
[4]PABLO M C, FARZAD I. Turn and zigzag maneuvers of a surface combatant using a URANS approach with dynamic overset grids[J]. Journal of Marine Science and Technology,2013,18:166-181.
[5]PABLO M C, ALEJANDRO M C. Self-propulsion computations using a speed controller and a discretized propeller with dynamic overset grids[J]. Journal of Marine Science and Technology,2010,15:316-330.
[6]RYAN G C. Improved underwater vehicle control and maneuvering analysis with computational fluid dynamics simulations[D].Virginia: Virginia Polytechnic Institute and State University,2013.
[7]ALEXANDER B P, STEPHEN R T. Evaluation of manoeuvring coefficients of a self-propelled ship using a blade element momentum propeller model coupled to a Reynolds averaged Navier Stokes flow solver[J]. Ocean Engineering,2009,36:1217-1225.
[8]吴召华.基于体积力法的船/桨/舵粘性流场数值研究[D].上海:上海交通大学,2013.
[9]王化明.双桨双舵船舶操纵性预报研究[J].武汉:武汉理工大学,2006,30(1):124-127.
Numerical Simulation and Analysis of
the Zig-zag Maneuvers of a Ship Model
XIANG GuoOU YongpengWU Hao
(NavalEngineeringDepartment,NavalUniv.ofEngineering,Wuhan430033,China)
Abstract:To study propeller thrust and the hydrodynamic variation of rudder in the process of maneuvering, based on URANS equation, combined with body force method, overset mesh technology, 6-DOF motion model, VOF model, taking into account the attitude of ship, a Zig-zag simulation of double propellers double tail fins and double rudders ship is launched , the numerical simulation results of the heeling, trim, overshoot angle, initial turning time and so on compared with the test results to verify the reliability of the numerical methods. On this basis, the time history curve of rudder force, rudder torque, propeller thrust and torque are analyzed and obtained in the zig-zag maneuvering motion.
Key words:body force method;Zig-zag;numerical simulation;overset mesh;rudder force;propeller thrust
收稿日期:2015-11-21
doi:10.3963/j.issn.2095-3844.2016.01.038
中图法分类号:U631.1

