“平面图形的认识（二）”测试卷

陆浩杰

一、 选一选

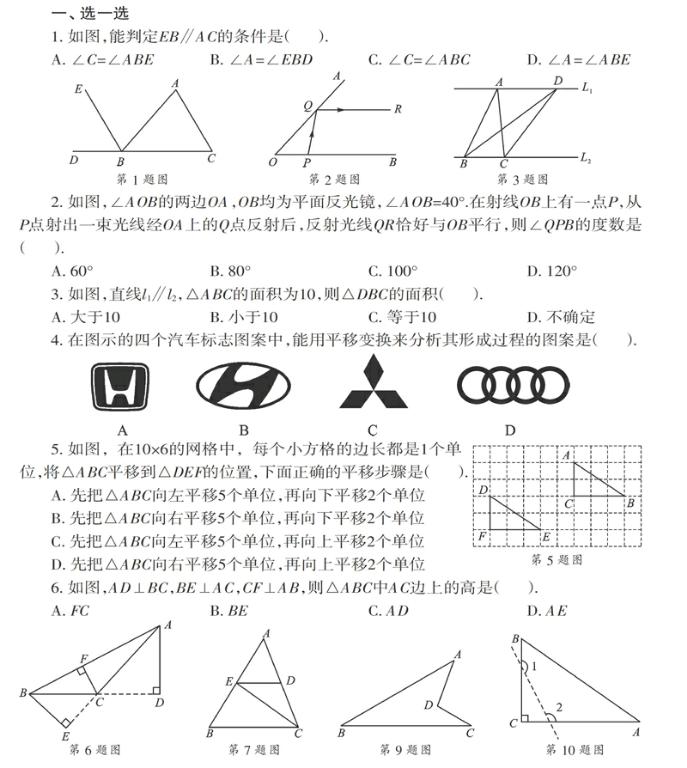
1. 如图，能判定EB∥AC的条件是（ ）.

A. ∠C=∠ABE B. ∠A=∠EBD C. ∠C=∠ABC D. ∠A=∠ABE

2. 如图，∠AOB的两边OA，OB均为平面反光镜，∠AOB=40°.在射线OB上有一点P，从P点射出一束光线经OA上的Q点反射后，反射光线QR恰好与OB平行，则∠QPB的度数是（ ）.

A. 60° B. 80° C. 100° D. 120°

3. 如图，直线l1∥l2，△ABC的面积为10，则△DBC的面积（ ）.

A. 大于10 B. 小于10 C. 等于10 D. 不确定

4. 在图示的四个汽车标志图案中，能用平移变换来分析其形成过程的图案是（ ）.

5. 如图，在10×6的网格中，每个小方格的边长都是1个单位，将△ABC平移到△DEF的位置，下面正确的平移步骤是（ ）.

A. 先把△ABC向左平移5个单位，再向下平移2个单位

B. 先把△ABC向右平移5个单位，再向下平移2个单位

C. 先把△ABC向左平移5个单位，再向上平移2个单位

D. 先把△ABC向右平移5个单位，再向上平移2个单位

6. 如图，AD⊥BC，BE⊥AC，CF⊥AB，则△ABC中AC边上的高是（ ）.

A. FC B. BE C. AD D. AE

7. 如图，已知在△ABC中，D，E分别为AC，AB的中点，且S△CDE=3，则S△ABC的值为（ ）.

A. 7 B. 10 C. 12 D. 14

8. 已知三角形的三边长分别为3、8、x，若x的值为偶数，则x的值有（ ）.

A. 6个 B. 5个 C. 4个 D. 3个

9. 如图所示是某零件的平面图，其中∠B=∠C=30°，∠A=40°，则∠ADC的度数为（ ）.

A. 70° B. 80° C. 90° D. 100°

10. 如图，已知△ABC为直角三角形，∠C=90°，若沿图中虚线剪去∠C，则∠1+∠2=（ ）.

A. 90° B. 135° C. 270° D. 315°

二、 填一填

11. 如图，已知∠1=∠2，∠B=40°，则∠3=_______.

12. 如图所示，CD是△ABC的中线，AC=9 cm，BC=3 cm，那么△ACD和△BCD的周长差是_______cm.

13. 如图，在△ABC中，作AB边中线CD，得到第一个三角形△ACD，在△DBC中作BC边中线DE，在△DBE中作BD边的中线EF，得到第二个三角形△DEF，在△BEF中作BE边中线FN，在△FNB中作BF边中线NP，得到第三个三角形△FNP，依次作下去，……若S△ABC=10，则第四个三角形的面积是_______.

14. 若等腰三角形两边长分别为3和5，则它的周长是_______.

15. 将正三角形、正四边形、正五边形按如图所示的位置摆放.如果∠3=32°，那么∠1+∠2=_______°.

16. 如图，在△ABC中，∠A=α，∠ABC的平分线与∠ACD的平分线交于点A1，得∠A1，∠A1BC的平分线与∠A1CD的平分线交于点A2，得∠A2，…，∠A2013BC的平分线与∠A2013CD的平分线交于点A2014，得∠A2014，则∠A2014=_______.

17. 如图，在△ABC中，∠BAC=40°，BP平分∠ABC，CP平分∠ACB，则∠BPC的度数为_______°.

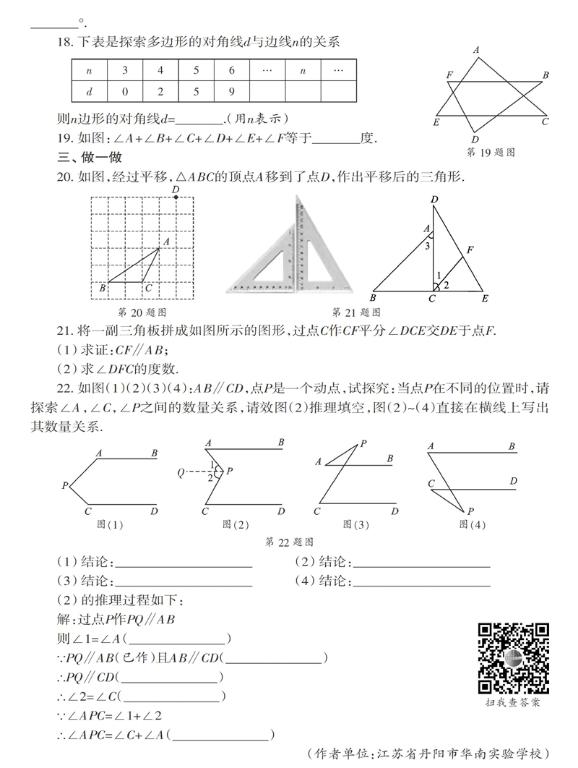
18. 下表是探索多边形的对角线d与边线n的关系

则n边形的对角线d=_______.（用n表示）

19. 如图：∠A+∠B+∠C+∠D+∠E+∠F等于_______度.

三、 做一做

20. 如图，经过平移，△ABC的顶点A移到了点D，作出平移后的三角形.

21. 将一副三角板拼成如图所示的图形，过点C作CF平分∠DCE交DE于点F.

（1） 求证：CF∥AB；

（2） 求∠DFC的度数.

22. 如图（1）（2）（3）（4）：AB∥CD，点P是一个动点，试探究：当点P在不同的位置时，请探索∠A，∠C，∠P之间的数量关系，请效图（2）推理填空，图（2）～（4）直接在横线上写出其数量关系.

（1） 结论：____________________ （2） 结论：____________________

（3） 结论：____________________ （4） 结论：____________________

（2） 的推理过程如下：

解：过点P作PQ∥AB

则∠1=∠A（______________）

∵PQ∥AB（已作）且AB∥CD（______________）

∴PQ∥CD（______________）

∴∠2=∠C（______________）

∵∠APC=∠1+∠2

∴∠APC=∠C+∠A（______________）

（作者单位：江苏省丹阳市华南实验学校）