探索生活中的角问题

沈轶群

角在我们的生活中无处不在，角的知识在实际生活中有很多的应用，下面我们一起来探索几个问题.

一、 钟表问题

例1 图1是一块手表，早上8时的时针、分针位置如图1所示，试求分针OA与时针OB所成的角的度数.

【分析与解】圆形钟面上共有12个大格，所以每大格所对应的角的度数为=30°，又由图1可知∠AOB包含了其中的4个大格，所以∠AOB=30°×4=120°.

二、 折叠问题

例2 把—张长方形纸条如图2所示那样折叠后，若得到∠AOB′=40°，试求∠B′OG的度数.

【分析】折纸问题中常包含许多有关线段和角的知识.寻找∠B′OG与∠AOB′的关系是解本题的关键.

解：因为∠B′OG是由原来的∠BOG沿直线OG对折过去的，故∠B′OG=∠BOG，又∠B′OB=∠B′OG+∠BOG=2∠B′OG=180°-40°=140°，所以∠B′OG=×140°=70°.

【说明】这是一类图形翻转折叠问题，解这类题时，要注意翻折前后的图形关于折痕成轴对称，即它们能够完全重合，对应的各线段相等，对应的各角相等.想想看，本例经折叠后除∠BOG=∠B′OG外，还有哪些角相等？哪些线段相等？

三、 方位角问题

例3 如图3在一张地图上，原标有学校、邮局、电影院三地，由于污损，电影院的具体位置已看不清，根据记忆，电影院位置在学校的北偏东30°的方向，在邮局的北偏西45°方向上.根据上述信息，你能在图上确定电影院的位置吗？如能，请画图说明.

【分析】根据题意，电影院位置在学校的北偏东30°方向上，作图时，应以学校所在地为测点在此处画上“十字型”，其上、下、左、右分别代表北、南、西、东方向.以正北方向的射线为始边，顺时针旋转30°，电影院就在所得的射线上；同理，在邮局的西北方向可作出另一条射线，这两条射线的交点，即为电影院所在的位置.

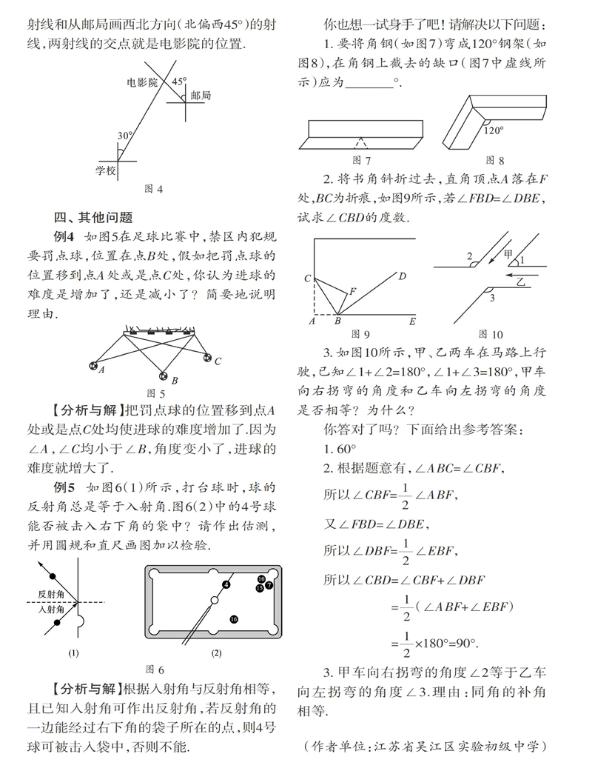
解：如图4分别从学校画北偏东30°的射线和从邮局画西北方向（北偏西45°）的射线，两射线的交点就是电影院的位置.

四、 其他问题

例4 如图5在足球比赛中，禁区内犯规要罚点球，位置在点B处，假如把罚点球的位置移到点A处或是点C处，你认为进球的难度是增加了，还是减小了？简要地说明理由.

【分析与解】把罚点球的位置移到点A处或是点C处均使进球的难度增加了.因为∠A，∠C均小于∠B，角度变小了，进球的难度就增大了.

例5 如图6（1）所示，打台球时，球的反射角总是等于入射角.图6（2）中的4号球能否被击入右下角的袋中？请作出估测，并用圆规和直尺画图加以检验.

【分析与解】根据入射角与反射角相等，且已知入射角可作出反射角，若反射角的一边能经过右下角的袋子所在的点，则4号球可被击入袋中，否则不能.

你也想一试身手了吧！请解决以下问题：

1. 要将角钢（如图7）弯成120°钢架（如图8），在角钢上截去的缺口（图7中虚线所示）应为_______°.

2. 将书角斜折过去，直角顶点A落在F处，BC为折痕，如图9所示，若∠FBD=∠DBE，试求∠CBD的度数.

3. 如图10所示，甲、乙两车在马路上行驶，已知∠1+∠2=180°，∠1+∠3=180°，甲车向右拐弯的角度和乙车向左拐弯的角度是否相等？为什么？

你答对了吗？下面给出参考答案：

1. 60°

2. 根据题意有，∠ABC=∠CBF，

所以∠CBF=∠ABF，

又∠FBD=∠DBE，

所以∠DBF=∠EBF，

所以∠CBD=∠CBF+∠DBF

=（∠ABF+∠EBF）

=×180°=90°.

3. 甲车向右拐弯的角度∠2等于乙车向左拐弯的角度∠3.理由：同角的补角相等.

（作者单位：江苏省吴江区实验初级中学）