基于蠕变试验的ZChSnSb11-6应力松弛特性研究

苗克军，王建梅，李　璞，徐俊良，张笑天，张亚南

(太原科技大学重型机械教育部工程研究中心，太原 030024)



基于蠕变试验的ZChSnSb11-6应力松弛特性研究

苗克军，王建梅，李璞，徐俊良，张笑天，张亚南

(太原科技大学重型机械教育部工程研究中心，太原 030024)

摘要：在相同温度下，对巴氏合金ZChSnSb11-6做了蠕变试验，获得合金在Norton形式和指数形式下的稳态蠕变方程，并利用所得系数得到合金在两种形式下应力松弛计算公式。采用ANSYS有限元分析软件模拟巴氏合金ZChSnSb11-6的应力松弛过程，得到松弛过程中的蠕变曲线，并比较了理论与有限元方法计算结果，两种方法相对误差不到0.5%。结果表明：在松弛过程中，Norton形式的蠕变速率比指数形式的蠕变速率小，且相比指数形式，Norton形式下的应力松弛计算公式精度更高，更适合于巴氏合金ZChSnSb11-6.

关键词：巴氏合金ZChSnSb11-6；应力松弛；蠕变试验；稳态蠕变方程；有限元分析

轧机油膜轴承广泛应用于钢铁、矿山、冶金、电力、航天、航空等关键设备，具有摩擦系数小、损耗低、刚性高等优点[1-2]。油膜轴承最薄弱的部分就是衬套巴氏合金，蠕变是其失效的一种形式[3-5]。蠕变为金属材料在受恒定应力作用下，应力与变形随时间变化的现象。应力松弛为金属材料变形不变，应力随着时间的增加而减少的现象，其本质是材料内部的弹性变形随着时间的增加逐渐转化成蠕变变形的过程[6]，应力松弛是蠕变的另一种表现形式[7]。

许多国内外学者对金属的应力松弛现象进行了研究。王明伟等[8]人通过高温应力松弛实验，分析了BT20钛合金的高温应力松弛行为。朱智等[9]人以不同温度和不同应力条件下的应力松弛试验为基础，建立了用于描述Hastelloy C-276合金应力松弛行为的蠕变本构方程。刘坡等[10]人以蠕变数据为基础预测了钛合金的应力松弛行为，且预测结果与实验结果吻合较好。Gary Paradee等[11]人研究了温度和应力对Sn96.5Ag3Cu0.5应力松弛行为的影响，并分析了其微观组织的变化。Mikael Segersäll等[12]人对镍基单晶高温合金的蠕变与应力松弛行为进行了研究。以上文献虽能提供一些分析合金应力松弛行为的方法，但均未涉及到对巴氏合金ZChSnSb11-6应力松弛行为的研究。

以蠕变试验为基础，得到巴氏合金ZChSnSb11-6的稳态蠕变方程，并通过蠕变与应力松弛之间的转换关系，得到巴氏合金ZChSnSb11-6的应力松弛特性，最后利用ANSYS有限元分析软件模拟了其应力松弛过程。

1蠕变试验

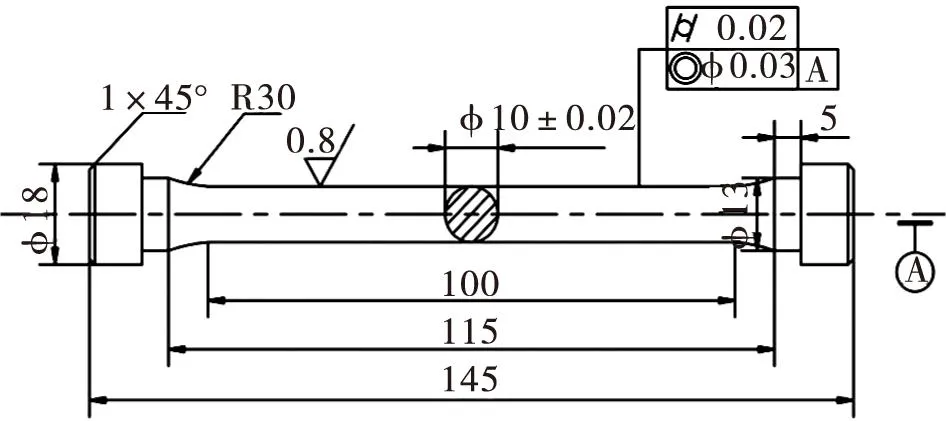
图1　蠕变试件几何示意图(单位mm)

图2　制蠕变试验设备

根据金属材料单轴拉伸蠕变试验方法[13]与巴氏合金ZChSnSb11-6的材料特性，设计了一套可以进行100 ℃以下蠕变试验的装置，蠕变试件几何形状示意图如图1所示。在原有WDW-E100D型万能试验机的基础上增加了YYU系列引伸计，加热带，TI200红外测温仪，加热罩等装置，实现了应变测量，加热，保温，测温，控温的功能，如图2所示。选择温度相同的13 MPa-60 ℃，18 MPa-60 ℃和20 MPa-60 ℃三组工况进行研究。

2巴氏合金ZChSnSb11-6稳态蠕变方程的建立

由蠕变试验，对蠕变数据进行求导处理，可得三种工况下的稳态蠕变速率，如表1所示。

由于选择的三组试验工况在相同温度下，故不考虑温度变化对蠕变变形的影响。选择以下两式建立巴氏合金ZChSnSb11-6的稳态蠕变方程，即[14-15]：

Norton形式：

(1)

指数形式：

(2)

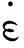
式(1)两边取对数得：

(3)

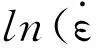
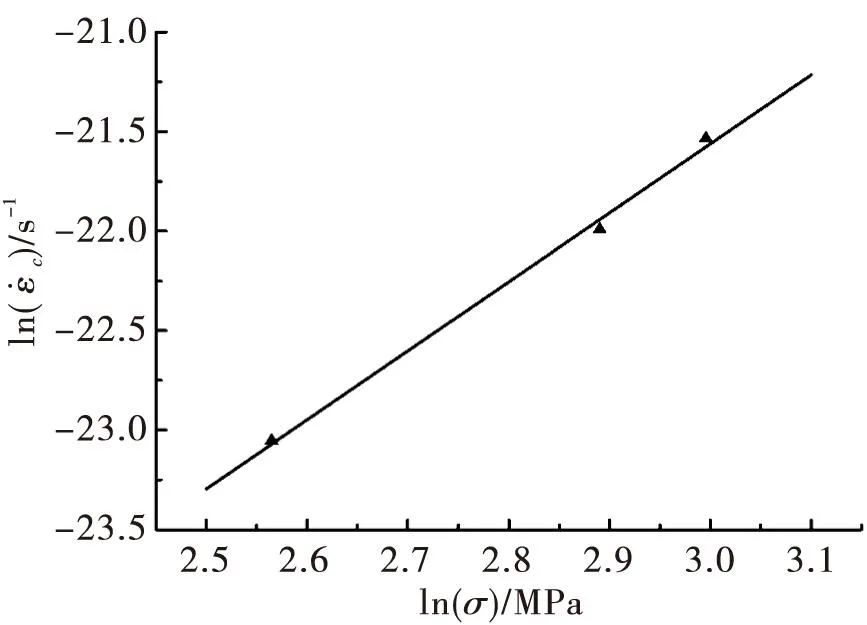
图与lnσ关系曲线

式(2)两边取对数得：

(4)

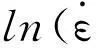
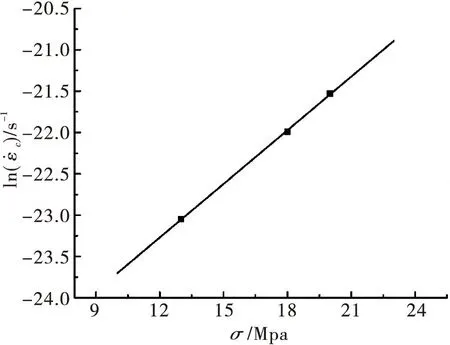
图与σ关系曲线

由图3和图4可得式(1)，式(2)中常数系数的值，如表2所示。

表2　系数的计算结果

将表2数据分别代入式(1)和式(2)，即可得到巴氏合金ZChSnSb11-6 Norton形式和指数形式的稳态蠕变方程。

3理论分析

3.1　以Norton关系稳态蠕变方程为对象的分析

在应力松弛中，设弹性应变为εe=σ/E，总应变为ε0，弹性系数为E，得[16]：

εe+εc=ε0=C

(5)

(6)

C为常数，根据式(1)和式(6)积分后，得到Norton形式稳态蠕变方程下，松弛的应力和时间的关系表达式式：

(7)

其中，σ0为t=0时的初应力，E=4.8e4 MPa.

将表1和表2数据代入式(6)，绘制Norton关系下巴氏合金ZChSnSb11-6的三组应力松弛曲线如图5所示，应力变化率曲线如图6所示。

由图5可知，温度相同时，巴氏合金ZChSnSb11-6在松弛的第一阶段随着初始应力的增加，应力变化率逐渐增加。在松弛的第二阶段，ZChSnSb11-6稳定后的应力随着初始应力的增加而增加。由图6可知，随着时间增加，应力变化率逐渐减小并趋于稳定。

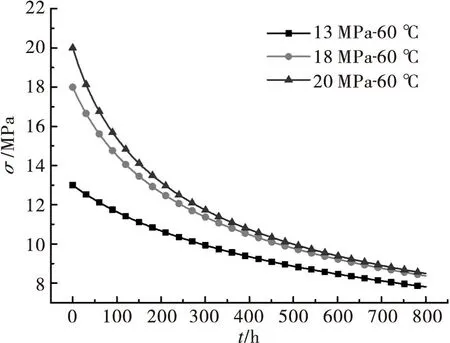
图5　Norton关系下ZChSnSb11-6的应力松弛曲线

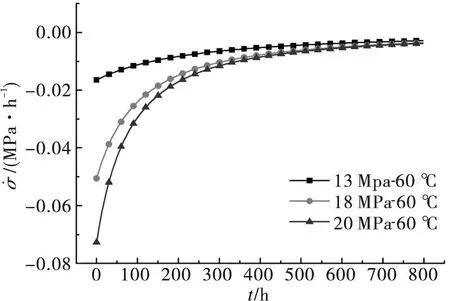
图6　Norton关系下ZChSnSb11-6的应力变化率曲线

3.2　以指数关系稳态蠕变方程为对象的分析

由式(2)式(6)联立可得指数关系稳态蠕变方程下，应力松弛的应力和时间的关系表达式：

(8)

将表1和表2数据代入式(7)，绘制巴氏合金ZChSnSb11-6的三组应力松弛曲线如图7所示。

由图7和图8可知，指数关系下ZChSnSb11-6的应力松弛与应力变化率的规律与Norton关系下ZChSnSb11-6的应力松弛变化规律基本相同，但在数值上存在一定的差异。

4有限元分析

4.1　模拟过程

利用ANSYS有限元软件，按蠕变试件的1/2几何尺寸建立巴氏合金ZChSnSb11-6的二维轴对称有限元模型，如图9所示。模拟过程保证总应变不变，温度设置为60 ℃，分别对初始应力为13 MPa，18 Mpa和20 Mpa三种工况进行应力松弛数值模拟。

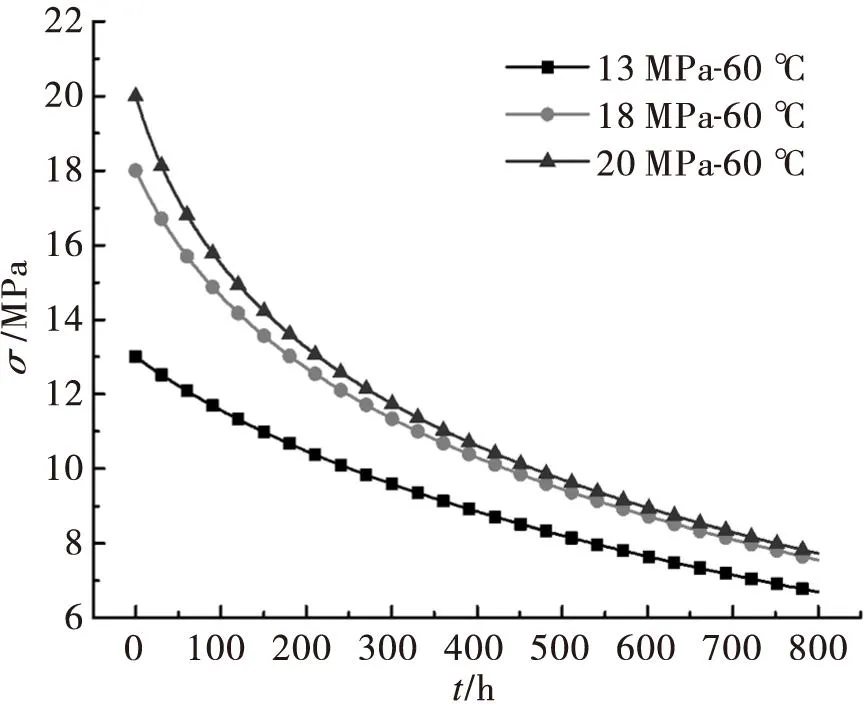
图7　指数关系下ZChSnSb11-6的应力松弛曲线

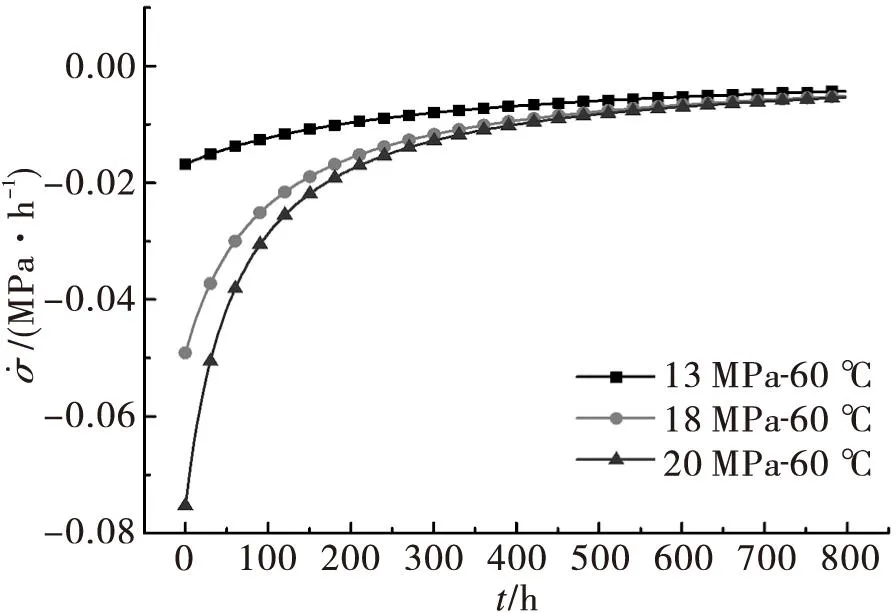
图8　指数关系下ZChSnSb11-6的应力变化率曲线

图9　巴氏合金ZChSnSb11-6有限元模型

ANSYS提供13种蠕变模型，选择其中用于计算稳态蠕变的两种模型分别计算：

TBOPT=10，Norton形式：

(9)

TBOPT=9，指数形式：

(10)

式中，c1~c3，b1~b3为ANSYS计算所需参数，本文不考虑温度变化的影响，故b3=c3=0，将式(9)和式(10)分别与式(1)和式(2)相对应求得：

c1=B=1.318 1e-14c2=n=3.466

b1=C=5.849 9e-12b2=d=4.625 3

4.2　结果与讨论

模拟巴氏合金ZChSnSb11-6试件松弛800 h后，二维模型各个位置的应力相等，故选择中间位置一点，分别绘制Norton形式和指数形式蠕变曲线如图10所示。

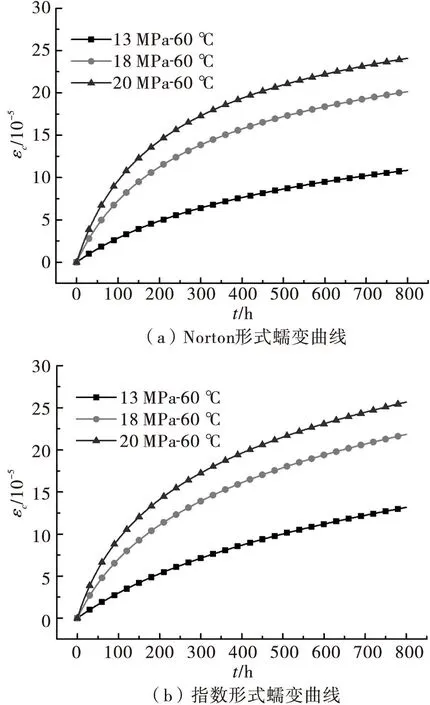
图10　应力松弛过程中的蠕变曲线

由图10可知，在巴氏合金ZChSnSb11-6的应力松弛过程中，蠕变随着时间的增加而逐渐增加，且逐渐趋于稳定。温度一定时，初始应力越大，蠕变越大。图10(a)可知，在800 h内，13 MPa，18 Mpa和20 Mpa三种工况Norton形式下的蠕变分别由0增加到1.09e-4，2.01e-4，2.41e-4，由图10(b)可知，指数形式下的蠕变分别增加到1.32e-4，2.18e-4和2.57e-4，说明在相同条件下，巴氏合金ZChSnSb11-6在松弛过程中Norton形式的蠕变速率比指数形式的蠕变速率小。

比较理论分析与有限元分析两种计算方法所得的应力松弛情况，计算公式为：

(11)

其中，Er为相对误差，T为理论计算结果，F为有限元计算结果。

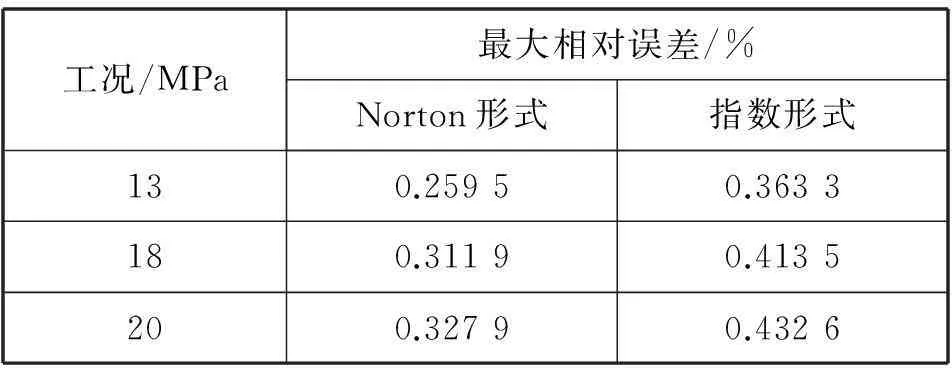
绘制两种方法的应力松弛相对误差曲线如图11所示，不同工况下最大相对误差如表3所示。

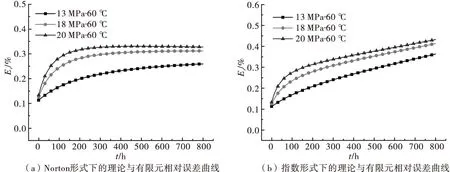
图11　理论与有限元的应力松弛相对误差曲线

工况/MPa最大相对误差/%Norton形式指数形式130.25950.3633180.31190.4135200.32790.4326

由图11可知，理论计算与有限元计算所得应力松弛相对误差不到0.5%，说明理论计算结果是正确的。随着时间的增加，两种形式的相对误差均趋于稳定，随着应力的增大，两种形式的相对误差均增大。

由表3可知，在三种工况下，Norton形式的最大相对误差均小于指数形式，说明相比指数形式，Norton形式下的应力松弛计算公式更适合于巴氏合金ZChSnSb11-6.

5结论

(1)通过蠕变试验，建立了巴氏合金ZChSnSb11-6Norton形式和指数形式的稳态蠕变方程，并得到两种形式下的应力松弛计算公式。

(2)利用ANSYS有限元软件模拟巴氏合金ZChSnSb11-6的应力松弛过程，结果表明三种工况下的蠕变随着时间增加而增加，且初始应力越大，蠕变也越大。松弛过程中Norton形式的蠕变速率比指数形式的蠕变速率小。

(3)对比理论与有限元两种方法所得应力松弛规律，两种方法的计算结果吻合较好，相对误差不到0.5%，且Norton形式的最大相对误差均小于指数形式，表明理论推导过程正确，Norton形式下的应力松弛计算公式更适合于巴氏合金ZChSnSb11-6.

参考文献：

[1]王建梅，黄庆学，丁光正.轧机油膜轴承润滑理论研究进展[J].润滑与密封，2012(10)：112-116.

[2]康建峰，王建梅，薛亚文，等.动压油膜轴承的摩擦性能及表面形貌分析[J].太原科技大学学报，2012(6)：455-460.

[3]王建梅，薛亚文，马立新，等.蠕变对巴氏合金 ZChSnSb11-6 力学性能和显微组织的影响[J].中国有色金属学报，2014，24(10)：2513-2518.

[4]王建梅，薛亚文，侯成，等.巴氏合金ZChSnSb11-6的蠕变特性[J].材料科学与工程学报，2013(6)：785-789+839.

[5]王建梅，薛亚文，蔡敏.油膜轴承巴氏合金ZChSnSb11-6衬套的蠕变寿命评估[J].上海交通大学学报，2015，49(1)：62-66.

[6]湛利华，王萌，黄明辉.基于蠕变公式的时效应力松弛行为预测模型[J].机械工程学报，2013，49(10)：70-76.

[7]穆霞英.蠕变力学[M].西安：西安交通大学出版社，1989.

[8]王明伟，王春燕，杨继新，等.BT20 钛合金高温应力松弛行为研究[J].稀有金属材料与工程，2012，41(3)：502-505.

[9]朱智，张立文，顾森东.Hastelloy C-276 合金应力松弛试验及蠕变本构方程[J].中国有色金属学报，2012，22(4)：1063-1067.

[10]刘坡，宗影影，郭斌，等.钛合金高温短时蠕变与应力松弛的关系研究[J].材料研究学报，2014，28(5)：339-345.

[11]GARY P，ERIC B，ARIS C.Stress relaxation behavior and low cycle fatigue behavior of bulkSAC 305[J].J Mater Sci：Mater Electron，2014，25：4122-4128.

[12]MIKAEL S，JOHAN JM，DANIEL L，et al.Creep and Stress Relaxation Anisotropy of a Single-CrystalSuperalloy [J].Metallurgical and Materials Transactions A，2014，45：2532-2544.

[13]中国钢铁工业协会.GB/T 2039-2012.金属材料单轴拉伸蠕变试验方法[S].北京：中国标准出版社，2012.

[14]尹旭妮，湛利华，赵俊.2219 铝合金稳态蠕变本构方程的建立[J].中国有色金属学报，2014，24(9)：2250-2256.

[15]杨松涛，李继文，魏世忠，等.纯钼板坯高温塑性变形行为及本构方程[J].中国有色金属学报，2011，21(9)：2126-2131.

[16]平修二.金属材料的高温强度理论设计[M].北京：科学出版社，1983.

Research on Stress Relaxation Characteristics of BabbittMetal ZChSnSb11-6 Based on Creep Test

MIAO Ke-jun，WANG Jian-mei，LI Pu，XU Jun-liang，ZHANG Xiao-tian，ZHANG Ya-nan

(Heavy Machinery Engineering Research Center of Education Ministry，Taiyuan University of Science

and Technology，Taiyuan 030024，China)

Abstract：Creep test of Babbitt metal ZChSnSb11-6 was conducted under the same temperature，steady state creep equation of Norton form and exponential form was respectively obtained，and formula of stress relaxation based on creep coefficients was acquired.Stress relaxation process of Babbitt metal ZChSnSb11-6 was simulated by ANSYS，creep curve in stress relaxation process was obtained and relative error curve of stress relaxation between theory method and finite element method was less than 0.5%.The results show that creep rate of Norton form was smaller than that of exponential form，and computational accuracy of Norton form was higher than those of exponential form，which show that formula of stress relaxation based on Norton form was more suitable for Babbitt metal ZChSnSb11-6.

Key words：Babbitt metal ZChSnSb11-6，stress relaxation，creep test，steady state creep equation，finite element analysis

中图分类号：TG146

文献标志码：A

doi：10.3969/j.issn.1673-2057.2016.01.009

文章编号：1673-2057(2016)01-0039-06

作者简介：苗克军(1990-)，男，硕士研究生，主要研究方向为机械设计及理论；通讯作者：王建梅，教授，E-mail：wjmhdb@163.com

基金项目：国家自然科学基金(51205269)；山西省回国留学人员科研资助(2013-093)

收稿日期：2015-05-18