2015年湖北高考(理)第14题的推广与简解
2016-03-02 11:52陈柏历
高中数学教与学 2016年1期
2015年湖北高考(理)第14题的推广与简解
陈柏历
(湖北省宜都市一中 高三(1)班,443300)

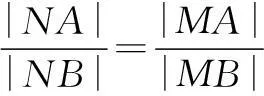
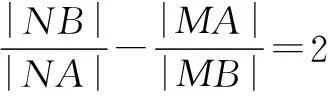

中正确的结论有______.
有些解析几何问题具有平面几何问题背景,利用平面几何推理方法进行论证,可避免繁琐的代数计算,简化问题处理过程.这里先给出结论的推广:
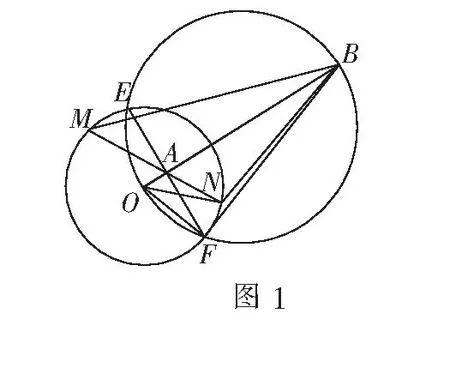
如图1,点B是半径为r的圆O外一定点,|OB|=d,以OB为直径的圆与圆O交于E,F两点,直线OB与直线EF交于点A,过A任作一直线交圆O于M,N两点,则下列三个结论都成立:

∠MBN);
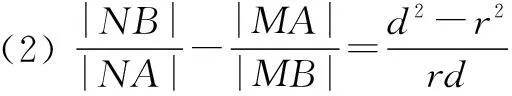

证明由圆的切线的定义,可知BF,BE为圆O的切线,且EF⊥OB.
由直角三角形射影定理,可得OF2=OA·OB,因OF=ON,故ON2=OA·OB.
又∠BON为公共角,故∆ONB∽∆OAN,有
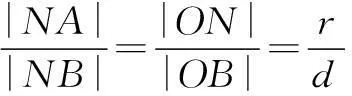
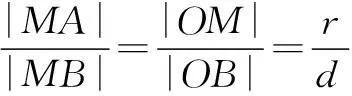


回到本道高考题中
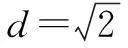
故本题所填答案为①② ③.
(指导老师:刘宜兵)
消去b,c,得
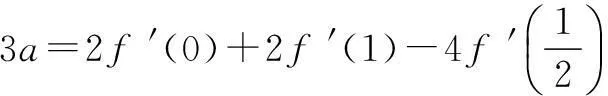
猜你喜欢
中学生数理化(高中版.高二数学)(2021年9期)2021-11-05
中学生数理化(高中版.高二数学)(2021年2期)2021-03-19
中学生数理化·高一版(2020年11期)2020-12-14
新世纪智能(数学备考)(2020年12期)2020-03-29
新世纪智能(数学备考)(2018年9期)2018-11-08
高中生·天天向上(2018年1期)2018-04-14
江西建材(2018年2期)2018-04-14
课程教育研究(2017年26期)2017-08-02
浙江柑橘(2016年3期)2016-03-11
浙江柑橘(2016年1期)2016-03-11

