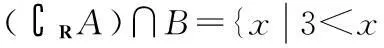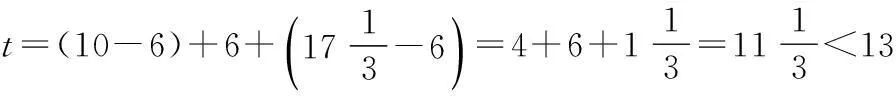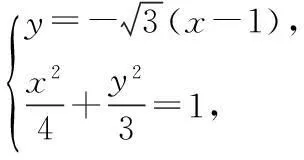用基底表示任意向量的三种基本方法



用基底表示任意向量的三种基本方法

张国坤

(云南省曲靖市第一中学，655000)

平面向量基本定理如果e1、e2是同一平面内不共线的两个向量,那么对于这个平面内的任一个向量a,有且只有一对实数λ1、λ2,使a=λ1e1+λ2e2.不共线的向量e1、e2叫做表示这一平面内的所有向量的一组基底.

那么,在具体操作中,怎样用e1、e2表示a呢?也就是如何确定λ1、λ2的值呢?有以下三种基本方法.

一、三角形法则或平行四边形法则

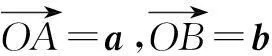
解法1(三角形法则)

已知点C在AB上，且AC=2CB,则

据三角形法则，有

解法2(平行四边形法则)

如图2，过点C作OB的平行线CD与直线OA相交于点D,过点C作OA的平行线CE与直线OB相交于点E.

已知AC=2CB,由平行线分线段成比例的规律及共线定理，得

二、待定系数共线法

解法1由A、E、C三点共线,可设

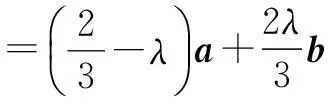
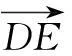
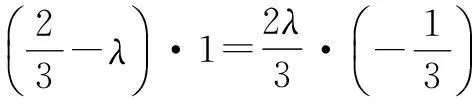
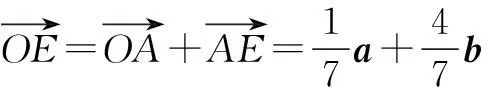
解法2由条件知

即2x+3y=2；

①

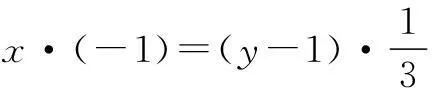
即3x+y=1.

②

三、待定系数“点乘”法

①

即a2x+abycos(α+β)=accosα；

②

即abxcos(α+β)+b2y=bccosβ.

③

联立② ③，得关于x、y的二元一次方程组,解之即得x、y的值.

解由余弦定理，得

OA是∆ABC外接圆半径,由正弦定理，得

①

6x-2y=-3；

②

3x-4y=2.

③

联立②③，解得

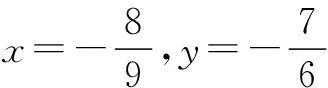
○课外测试○

高一数学测试

一、填空题(本大题共14小题,每小题5分,共70分)

1.若集合A={1,2},B={-2,1},则A∪B=______.

2.函数f(x)=lg(3x-2)的定义域为______.

4.函数y=ax+1(a>0,a≠1)过定点______.

5.函数f(x)=|x-1|的单调递增区间是______.

6.已知函数f(x)=ax3+bx+1,且f(a)=6,则f(a)=______.

8.已知a=log1.20.6,b=1.20.6,c=log0.50.6,则a,b,c从小到大排列依次为______.

9.方程log3x=3-x的解在区间(n,n+1)内，n∈N*，则n=______.

11.已知f(x)=x|x+1|,则

的解集是______.

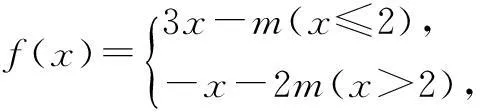
二、解答题(本大题共6小题,共计90分,解答时应写出文字说明、证明或演算步骤)

(1)若m=3,求(RA)∩B;

(2)若A∪B=A,求实数m的取值范围.

16.(本小题满分14分)已知函数

(1)证明:函数f(x)在(1,+∞)上递减;

(2)记函数g(x)=f(x+1)-1,判断函数g(x)奇偶性,并加以证明.

17.(本小题满分15分)已知函数f(x)=x2-ax+3在区间(-∞,2)上是减函数,在区间[2,+∞)上是增函数.

(1)求a的值;

(2)求函数f(x)在区间[0,3]的值域;

(3)求函数f(x)在区间[0,m](m>0)上的最大值g(m).

18.(本小题满分15分)心理学家通过研究学生的学习行为发现:学生的接受能力与老师引入概念和描述问题所用的时间相关.教学开始时,学生的兴趣激增,学生的兴趣保持一段较理想的状态,随后学生的注意力开始分散,分析结果和实验表明,用f(x)表示学生掌握和接受概念的能力,x表示讲授概念的时间(单位:min),可有以下的关系:

(1)开讲后第5 min与开讲后第20 min比较,学生的接受能力何时更强一些?

(2)开讲后多少min学生的接受能力最强?能维持多少时间?

(3)若一个新数学概念需要55以上(包括55)的接受能力以及13 min时间,那么,老师能否在学生一直达到所需接受能力的状态下讲授完这个概念?

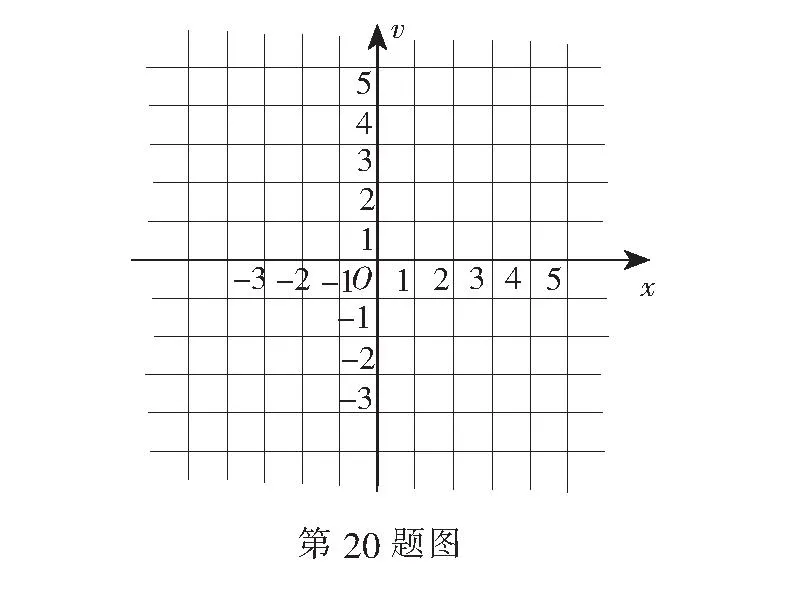
19.(本小题满分16分)已知函数f(x)是定义在(-4,4)上的奇函数,当-4

(1)求实数a,b的值,并求函数f(x)的解析式;

(2)若关于x的方程f(x)=m有两个不同的实数解,请写出实数m的取值范围;

(3)解关于x的不等式(x-1)f(x)<0.

20.(本小题满分16分)已知函数

f(x)=|x2-1|+x2-kx.

(1)若k=2,作出函数y=f(x)的图象,并根据图象写出函数的单调区间;

(2)若f(x)≥0恒成立,求实数k的取值范围;

(3)若关于x的方程f(x)=0在(0,+∞)上有两个不同的解x1,x2,试比较f(x1x2)与1-k的大小.

参考答案

一、填空题

4.(0,2);5.(1,+∞);6.-4;7.-2;

二、解答题

(1)当m=3时,RA={},集合B={<7},于是

(2)因为A∪B=A,所以B⊆A.

16.(1) 设x1>x2>1,则x2-x1<0,x1-1>0,x2-1>0.

∴f(x1)

∴f(x)在(1,+∞)上递减.

∴g(x)是奇函数.

17.(1)∵f(x)=x2-ax+3在区间(-∞,2)上是减函数,在区间[2,+∞)上是增函数,

(2)∵f(x)=x2-4x+3在[0,2]上递减,在[2,3]递增,

∴f(x)min=f(2)=-1.

∵f(0)=3,f(3)=0,∴f(x)max=f(3)=3,

∴f(x)值域为[-1,3].

18.(1)∵f(5)=53.5,f(x)=47,∴f(5)>f(20),

∴开讲后第5 min比开讲后第20 min,学生的接受能力更强些.

(2)当0

∴当x=10时,f(x)max=f(10)=59；

当x>16时,f(x)<-3×16+109=59.

∴开讲后10min(包括10分钟)学生的接受能力最强,能维持6 min.

(3)由函数f(x)=

当1

答:老师不能在学生一直达到所需接受能力的状态下讲授完这个概念.

19.(1)由f(-3)=0,f(-2)=1,得

loga(-3+b)=0,loga(-2+b)=1,

∴a=2,b=4,

∴-4

设0

∴f(-x)=log2(-x+4).

∵f(x)是定义在(-4,4)上的奇函数,

∴f(-x)=-f(-x)=-log(-x+4)，且f(0)=0,

(2)当-4

当0-2.

要使方程f(x)=m有两个不同的实数解应满足-2

所以-2

∴1

∴-3

20.(1)k=2时,

图略.由图可知,f(x)单调减区间(-∞,1),单调增区间(1,+∞).

-1

∴-1≤k≤1.

综上所述，k的取值范围是[-1,1].

∴方程-kx+1=0在(0,1)上必有一根,

∴k>1,此时x2>1,

∵k>1,∴0

∵k>1时，f(x)在(0，1)上递减,

∴f(x1x2)>f(1),而f(1)=1-k,

∴f(x1x2)>1-k.

高二数学测试

一、填空题(本大题共14小题,每小题5分,共70分)

2.命题p:“∀x∈R,x2+2x-3≥0”,命题p的否定为______.

3.“一条直线与两个相交平面都平行”是“这条直线与这两个平面的交线平行”的______条件.(在“充分不必要”,“必要不充分”,“充要”,“既不充分也不必要”中选填)

4.等轴双曲线的离心率等于______.

6.火星的半径约是地球半径的一半, 则地球表面积约是火星表面积的______倍.

8.已知直线l⊥平面α,直线m⊂平面β，给出下列命题：

①若α∥β，则l⊥m;

②若α⊥β，则l∥m;

③若l∥m,则α⊥β；

④若l⊥m,则α∥β.

其中,正确命题的序号是______.(写出所有正确命题的序号)

10.长方体ABCD-A1B1C1D1中，AB=BC=3，AA1=2,则四面体A1BC1D的体积为______.

12.已知命题p:“∀x∈R,∃m∈R,4x-2x+1+m=0”,若命题p是假命题,则实数m的取值范围是______.

13.已知椭圆C的左右焦点分别为F1,F2,过F1且斜率为2的直线交椭圆C于P,Q两点,若∆PF1F2为直角三角形,则椭圆的离心率为______.

二、解答题(本大题共6小题,共计90分.解答应写出文字说明、证明过程或演算步骤)

15.(本小题满分14分)如图,斜三棱柱ABC-A1B1C1中,侧面AA1C1C是菱形,AC1与A1C交于点O,E是AB的中点.

(1)求证:OE∥平面BCC1B1;

(2)若AC1⊥A1B,求证:AC1⊥平面A1BC.

(1)求椭圆的标准方程;

(2)求以椭圆焦点为顶点且离心率与椭圆的离心率互为倒数的双曲线的标准方程.

17.(本小题满分14分)已知a∈R,命题p:“∀x∈[1,2],x2-a≥0”,命题q:“∃x∈R,x2+2ax+2-a=0”.

(1)若命题p为真命题,求a的取值范围;

(2)若命题“p∨q”为真命题,命题"p∧q"为假命题,求a的取值范围.

18.(本小题满分16分)如图,在三棱锥P-ABC中,∆PAB和∆CAB都是以AB为斜边的等腰直角三角形,D、E、F分别是PC、AC、BC的中点.

(1)证明:平面DEF∥平面PAB;

(2)证明:AB⊥PC;

19.(本小题满分16分)请你设计一个包装盒,如图所示.ABCD是边长为60 cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得ABCD四个点重合,正好形成一个正四棱柱形状的包装盒(不考虑拼接等损耗),E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm.

(1)将包装盒的侧面积S(cm2)表示成x的函数,并写出x的范围;

(2)若广告商要求包装盒侧面积S最大,试问x应取何值?并求此时S的值.

(2)当a2+b2=4时,设M为椭圆C上第一象限内的点,直线l交y轴于点Q，F1M⊥F1Q,证明:点M在定直线上.

参考答案

一、填空题

1.6;2.∃x∈R,x2+2x-3<0;

二、解答题

15.(1) 连结BC1.

∵侧面AA1C1C是菱形,AC1与A1C交于点O,

∴O为AC1的中点.

∵E是AB的中点, ∴OE∥BC1.

∵OE⊄平面BCC1B1,BC1⊂平面BCC1B1,

∴OE∥平面BCC1B1.

(2)∵侧面AA1C1C是菱形, ∴AC1⊥A1C.

∵AC1⊥A1B,A1C∩A1B=A1,

A1C⊂平面A1BC,A1B⊂平面A1BC,

∴AC1⊥平面A1BC.

17.(1)命题p:“∀x∈[1,2],x2-a≥0”为真命题.

令f(x)=x2-a,根据题意,只要x∈[1,2]时，f(x)min≥0即可，

也就是1-a≥0⟹a≤1.

(2)由(1)可知,当命题p为真命题时,a≤1.

命题q为真命题时,Δ=4a2-4(2-a)≥0,解得a≤-2或a≥1.

因为命题“p∨q”为真命题,命题“p∧q”为假命题,所以命题p与命题q一真一假.

当命题p为真,命题q为假时,

当命题p为假,命题q为真时,

综上,a>1或-2

18.(1)∵E、F分别是AC、BC的中点,

∴EF∥AB.

∵AB⊂平面PAB,EF⊄平面PAB,

∴EF∥平面PAB, 同理DF∥平面PAB.

EF∩DF=F，且EF⊂平面DEF,DF⊂平面DEF,

∴平面DEF∥平面PAB.

(2)AB的中点G,连结PG、CG.

∵∆PAB和∆CAB都是以AB为斜边的等腰直角三角形,

∴PG⊥AB,CG⊥AB.

∵PG∩CG=G, 且PG⊂平面PCG,CG⊂平面PCG,∴AB⊥平面PCG.

∵PC⊂平面PCG, ∴AB⊥PC.

(3)在等腰直角三角形PAB中,

∵AB⊥平面PCG,

其侧面积

S=4ah=-8(x2-30x),0

(2)S=-8(x-15)2+1 800.

当x=15时,S有最大值1 800.

20.(1)设F2(c,0),则

(2)设M(x0,y0)(x0>0,y0>0),F2(c,0),则

直线l的方程为

由F1M⊥F1Q,可知

又c2=a2-b2=2a2-4,

所以点M在定直线x+y=2上.

一道高考数学压轴题的简便解法及应用

程汉波杨春波

(广东省广州市第二中学,510040)(河南省郑州外国语学校,450001)

(1)、(2)(略);

(3)记g(x)=|f′(x)|(-1≤x≤1)的最大值为M，若M≥k对任意的b,c恒成立,试求k的最大值.

此压轴题构思精巧,涉及到导数、绝对值、不等式与最值等知识点,而且将其融合在一个新的定义运算情境之中,耐人寻味.后期统计发现该题第(3)问得分率极低,遗憾的是之后关于该题的研究也很少,很多师生都觉得参考答案中缜密而复杂的讨论不可避免.笔者近日又偶遇此题,意外之中得到了一个巧妙的解法,并且很容易将该题拓广,介绍如下,供参考.

M≥f(1)=|1-2b-c|,

M≥f(-1)=|1+2b-c|,

M≥f(0)=|c|.

于是4M≥f(1)+f(-1)+2f(0)

≥|1-2b-c+1+2b-c+2c|=2,

该解答利用绝对值不等式,并结合最值定义利用特殊值使问题巧妙得解.类似地，我们可解决如下的最值问题：

例1已知函数f(x)=ax3+bx2+cx+d(a≠0),当-1≤x≤1时,有|f′(x)|≤M恒成立,求a的最大值.

解由已知得f′(x)=3ax2+2bx+c,故

消去b,c，得

6a=f′(1)+f′(-1)-2f′(0),

所以6|a|=|f′(1)+f′(-1)-2f′(0)|≤|f′(1)|+|f′(-1)|+2|f′(0)|≤4M,

例2(2010年全国数学竞赛联赛题)已知函数f(x)=ax3+bx2+cx+d(a≠0),当0≤x≤1时，有|f′(x)|≤1,试求a的最大值.

解由已知，得f′(x)=3ax2+2bx+c,于是有

○高考之窗○