基于纯方位信息的目标跟踪线性修正模型*
刘进忙,张春梅,甘林海,王迎春
(空军工程大学,陕西西安 710051)
基于纯方位信息的目标跟踪线性修正模型*
刘进忙,张春梅,甘林海,王迎春
(空军工程大学,陕西西安710051)
摘要:在基于几何关系的纯方位航迹不变量信息处理过程中,对非线性模型进行细致分析,提出了线性修正模型,在处理问题时更加清晰、可靠,减小了大量的计算和计算误差,使纯方位信息的非线性处理实用化。
关键词:几何定理;目标跟踪;纯方位信息
修回日期: 2015-12-10
张春梅(1978-),男,讲师。
甘林海(1991-),男,硕士研究生。
王迎春(1986-),男,博士研究生。
方位信息是飞行目标的重要信息,包含了飞行目标航迹的方向信息,对目标定位、跟踪有重要的作用[1-2]。在红外跟踪系统中,一般的数据采样率为15-30次/S,可近似认为机动目标作匀速直线运动。对预警雷达而言,由于目标距离较远,一般都假定目标作匀速直线飞行。纯方位信息计算目标的航向角和预测方位角度将会引入较多的非线性计算[3-11]。作者经过详细理论分析,认为可由线性模型和修正项来实现方位的预测和估计,使计算尽可能简单、可靠,减少了中间环节。仿真试验进一步验证了该方法有效性。
1几何关系定理
1)定理:如图1所示,若B点将AC分成L1、L2段,则
L1cotα3+L2cotα1=(L1+L2)cotα2
(1)
可采用测高公式证明,在此略。可选左侧角度,上式不变。
2)推论:当L1=L2时,有
cotα1+cotα3=2cotα2
(2)

图1 三角形的余切关系
若PB′是∠APC的角平分线,则有
(3)
根据三角形外角关系,存在
(4)
代入式(3),即有关系:
α1-2α2+α3=2θ
(5)
为求θ,以B′点的余切关系:
(6)
求出

(7)
在△BB′P中,由正弦定理可知
(8)
在△ABP中,由正弦定理可知
(9)
将式(7)、(9)代入式(8)可得

(10)
由此可见,θ与α1,α2,α3存在非线性关系。
2平面坐标系纯方位信息的预测线性修正模型
设P点为传感器的位置,目标沿直线运动,A、B、C、D为时间分别为t1,t2,t3,t4的目标位置点,βi为所对应的目标位置的方位值,则目标航迹水平面投影图,如图2所示。

图2 目标航迹水平面投影图
将αi=α0-βi(i=1,2,3,…)代入式(5),可得线性修正模型:
β3=2β2-β1-2θ
(11)
显然,由于θ的出现限制了βi的线性增长。
将平面关系代入式(10),可得
(12)
对式(11)、(12)进一步联合处理可得

(13)
由式(13)可计算出目标航迹直线的方位角:
(14)
3近似计算
由于在式(12)中包含了β3,故需要对式(12)可进一步近似:
β3-β1≈2(β2-β1),cos(β3-β1)≈1
β1+β3≈2β2
(15)
则式(12)可进一步近似为
sinθ=cot(α0-β2)sin2(β2-β1)
(16)
式(14)可近似为
(17)
4仿真算例
设测量系统在坐标原点,采样周期为0.1s,空中目标初始化位置为(0m,4000m),目标作匀速直线运动,目标速度200m/s,航向角(与正北方向夹角)为π/3,对目标进行100次测量,测量误差均值为0,方差为0.01的高斯白噪声,利用线性修正模型对目标方位进行预测和估计,由于传感器采样频率较高,故仿真中取10个采样点角度的平均值来进行计算,这样可以减少测量误差的影响,仿真结果如图3、图4所示。

图3 匀速直线运动估计结果对比(去野值前)
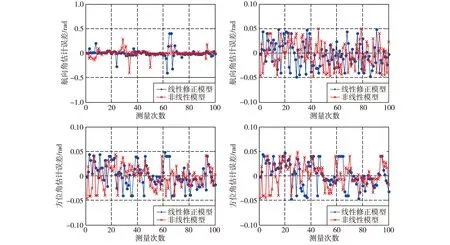
图4 匀速直线运动估计结果对比(去野值后)
由仿真结果可以看出,所提出的线性修正模型可以有效的对目标的方位角进行预测和估计,并且与非线性模型误差相当,其优点是计算简单、可靠,因此,线性修正模型更易于工程实现,仿真试验进一步验证了该方法有效性。
5结束语
利用线性修正模型避免繁杂的非线性计算,极大地方便了纯方位的匀速直线运动的目标跟踪,对算法的工程应用起到了重要作用,仿真结果进一步表明此方法是实用和可靠的,该算法已在有关科研项目中得到应用,效果良好。
参考文献:
[1]Multiple Autonomous Robotic Systems Labraratory-Bearing-only tracking using bank of MAP estimators, TR2010-0001[R]. Minneapolis: Department of Computer Science & Engineering University of Minnesota, 2010.
[2]刘进忙. 空中分坐标滤波与参数航迹融合技术研究[D].西安:西安电子科技大学, 2012.
[3]鹿传国, 冯新喜, 张迪. 基于改进容积卡尔曼滤波的纯方位目标跟踪[J]. 系统工程与电子技术, 2012, 34(1): 28-33.
[4]黄波, 刘忠, 吴玲. 纯方位目标运动状态的极大似然估计及迭代算法[J]. 海军工程大学学报, 2013(1):54-58.
[5]郁涛. 固定单站纯方位目标运动参数的解析方法[J]. 电波科学学报, 2014(6):4-8.
[6]石杰, 戚国庆, 盛安冬. 基于非质点模型的纯方位解距离方法[J]. 计算机与数字工程, 2013, 41(7): 1070-1073.
[7]董志荣.舰艇指控系统的理论基础[M].北京:国防工业出版社, 1995.
[8]D.C.Chang, M.W.Fang. Bearing-Only Maneuvering Modile Tracking With Nonlinear Filtering Algorithms in Wireless Sensor Networks[J]. Systems Journal, IEEE, 2014, 8(1): 160-170.
[9]刘进忙,姬红兵,左涛.纯方位观测的航迹不变量目标跟踪算法[J].西安电子科技大学学报,2008(2):49-53
[10]Bonneton F,Jauffret C.Bearing Line Tracking and Bearing-Only Target Motion Analysis[C]∥Aerospace Conference.Big Sky:IEEE,2007:1-9.
[11]Ho K C,Chan Y T.An Asymptotically Unbiased Estimator for Bearings-Only and Doppler-bearing Target Motion Analysis[J].IEEE Trans on Signal Processing,2006,54(3):809-822.
Research on Linear Amendatory Model of Target Tracking Problem Based on Bearing-only Measurement
LIU Jin-mang, ZHANG Chun-mei, GAN Lin-hai, WANG Ying-chun
(Air Force Engineering University, Xi’an 710051, China)
Abstract:A new linear amendatory model is proposed for target tracking based on bearing-only measurement. Compared with the nonlinear model,the linear amendatory model is more clear and credible, reduced the calculate error effectively.It also makes the engineering using widely.
Key words:geometry theorem;target tracking;bearing-only measurement
作者简介:刘进忙(1958-),男,陕西渭南人,教授,博士生导师,研究方向为信息融合理论及应用。
*基金项目:国家自然科学基金(60677040)
收稿日期:2015-11-25
中图分类号:TN953;E911
文献标志码:A
DOI:10.3969/j.issn.1673-3819.2016.01.001
文章编号:1673-3819(2016)01-0001-03

