基于熵理论的网络空间作战指挥系统结构优化研究*

王南星,王劲松,李国伟

(解放军信息工程大学,河南郑州　450001)



基于熵理论的网络空间作战指挥系统结构优化研究*

王南星,王劲松,李国伟

(解放军信息工程大学,河南郑州450001)

摘要:作战指挥系统的优劣程度,通常用系统内信息传递的及时性和准确度两项指标进行衡量,结构熵理论中时效和质量两种度量方式可以有效地对这两项指标进行定量分析。运用这一理论对网络空间作战指挥系统的传统型构建方式和改进型构建方式分别建立了系统有序度模型,结合实例进行评价分析,从而论证两种作战指挥系统结构优劣程度,为网络空间作战指挥体系的构建提供参考。

关键词:熵理论;网络空间；作战指挥;有序度;优化

修回日期： 2015-11-27

王劲松(1965-),男,教授,硕士生导师。

李国伟(1984-),男,硕士研究生。

网络空间作战指挥是指挥员为达成特定作战目的,对网络空间作战行动进行的决策计划、组织指挥、协调控制和效能评估等活动。近几场局部战争表明,网络空间作战指挥活动中指挥关系、指挥手段、指挥方式、指挥环境等因素决定网络空间作战行动的成败。运用熵理论对网络空间作战指挥系统结构的构建进行评估分析,实现系统结构的优化和功能的释放,对建立网络空间作战指挥系统具有重要意义。

1概述[1-3]

在传统的指挥系统中,信息的流通更多地体现在上、下级之间的纵向流通,作战任务的下达基于部队武器装备技战术性能,指挥信息的流通呈现出独立的线性结构。而网络空间作战行动更加依赖于信息,作战任务需要各要素协力配合完成。信息不仅在指挥系统内纵向流通,各要素间的横向流通也成为网络空间作战指挥的显著特点。作战指挥系统对各要素的协调控制和各要素间的相互联通使得信息的流通较以往作战更加复杂,各要素对信息的共享和分配都提出了更高的需求。总体上看,前者是根据自身武器装备性能组织指挥控制;后者是根据任务需求协调控制各类武器装备。

1850年,鲁道夫·克劳修斯首次提出熵的概念,用来表示一种能量在空间中分布的混乱程度,能量分布得越混乱,熵就越大。熵理论的不断发展使其成为度量与测量组织结构复杂性的研究中一个主要的研究分支。结构熵模型理论是应用范围非常广泛的一门科学理论,熵既是一个物理学概念,又是一个数学函数,也是一种自然法则[4]。

文献[5-9]中使用了结构熵模型对指挥系统进行建模,并用时效和质量两个指标对指挥效益进行了评价。文献[5]的实例分析在指挥层级和要素组成不一致的情况下得出改进后的指挥系统效率高于原始状态;文献[6]中在两作战系统构成相差悬殊的条件下,得出美军指挥系统效率高于俄军;文献[7]采用了相同的指挥层级和要素组成进行对比分析,但在计算质量实现概率中存在明显偏差,最终仍得出基于作战任务建立的指挥系统比基于武器结构建立的指挥系统效率更高;文献[8]总结了早期有关熵理论文献中的不足,构建了改进的时效有序度模型,阐述了权重系数的分配应针对不同系统而设定,并指出“当组成系统的元素个数一定时,结构高时效有序度和高质量有序度不可兼得,总存在一优一劣的状况[8]”。但在文献[9]中通过多链路共享信息的组合模式,使得元素个数相同时,时效和质量同时提升存在可能。文献[9]在时效和质量两种指标的基础上增加了可靠度指标,对于综合效率的评价采用三者的算术平均数,没有对三者的权重系数进行讨论分配。本文以及时性和准确度作为指挥系统衡量标准,基于熵理论从时效和质量两个指标建立结构有序度模型,定义各指标的含义并依此建立系统特征表达,并进行计算分析得出结论。

2作战指挥系统有序度模型的建立

信息效用指信息满足需要的能力。信息越能满足需要,其效用就越大。如采用基数效用理论,则信息效用是可以度量的,衡量单位为“信息效用量”(information utility)[10-11]。由此,在对系统进行结构有序度评价时,可采用时效性和质量性两个“信息效用量”进行定量分析。时效性表示信息传递的及时性,质量性表示信息传递的准确度。在结构熵模型中时效熵是信息传递时间不确定性的度量,用时效表示系统在时效性方面的有序度;质量熵是信息传递质量不确定性的度量,用质量表示系统在准确性方面的有序度。将两者进行综合对系统组织进行整体评价。

在对系统组织结构定量化描述中,系统有序度表示系统的复杂及有序程度。通常用R=1-H/Hmax表示。其中,R表示系统组织有序度,H表示系统组织结构熵,Hmax表示系统组织最大熵(从数学角度分析,存在Hmax=0的情况,但在实际组织结构中基本不存在点对点的单一指挥关系结构,所以本文不考虑这种极端情况);R越大,表示系统有序化程度越高、结构越优。

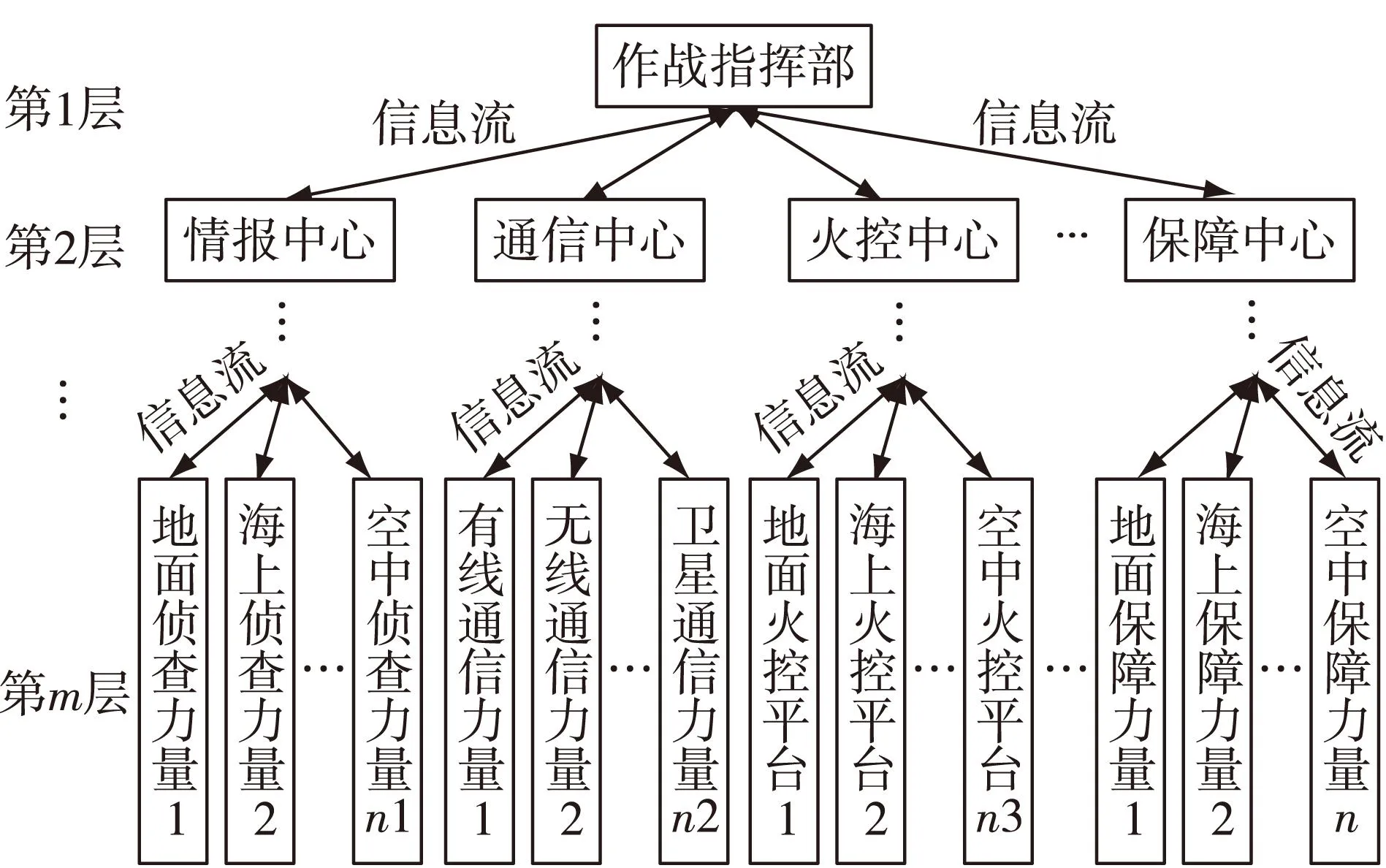
图1　联合作战指挥系统组织结构图

图1为联合作战指挥系统组织结构图,在该拓扑结构中共有n个元素和m层指挥层次。其中“—”代表两元素间存在信息直接联系。下面以此模型为例,对系统组织结构中各项指标进行定义。

2.1指挥系统组织结构时效有序度模型

在指挥系统组织结构中,信息的流动指在指挥控制关系网上的信息流动[10],反映着指挥信息的下达与反馈。图2为某防空想定指挥控制图[11],图中箭头表示信息在该指挥控制系统中的流动及方向,从指挥部、武器平台、探测器到单兵。信息流将指挥命令和反馈信息传输至系统的每一个元素,构成完整的信息流回路,从而完成指挥控制的整个流程。

系统中任何两个节点之间都有可能进行信息的交流,那么系统中任意两元素的时效熵定义为

(1)

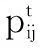
系统总的时效熵定义为

(2)

n表示系统中总元素个数,定义系统最大时效熵为

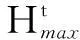
(3)

其中，An为系统中时效微观态总数,时效微观态为系统中两元素联系的状态数。

(4)

Lij为系统中i,j两元素间的联系长度,以两者间取得联系的最短路径来计算。由于效率表示单位时间信息的流通量,所以取系统内直接关联的两元素长度为1,每次信息中转后长度加1。如在图1中,“作战指挥部”与“情报中心”的联系长度为“1”,“作战指挥部”与“地面侦查力量1”的联系长度为“m-1”。

定义i,j实现转移的概率:

(5)

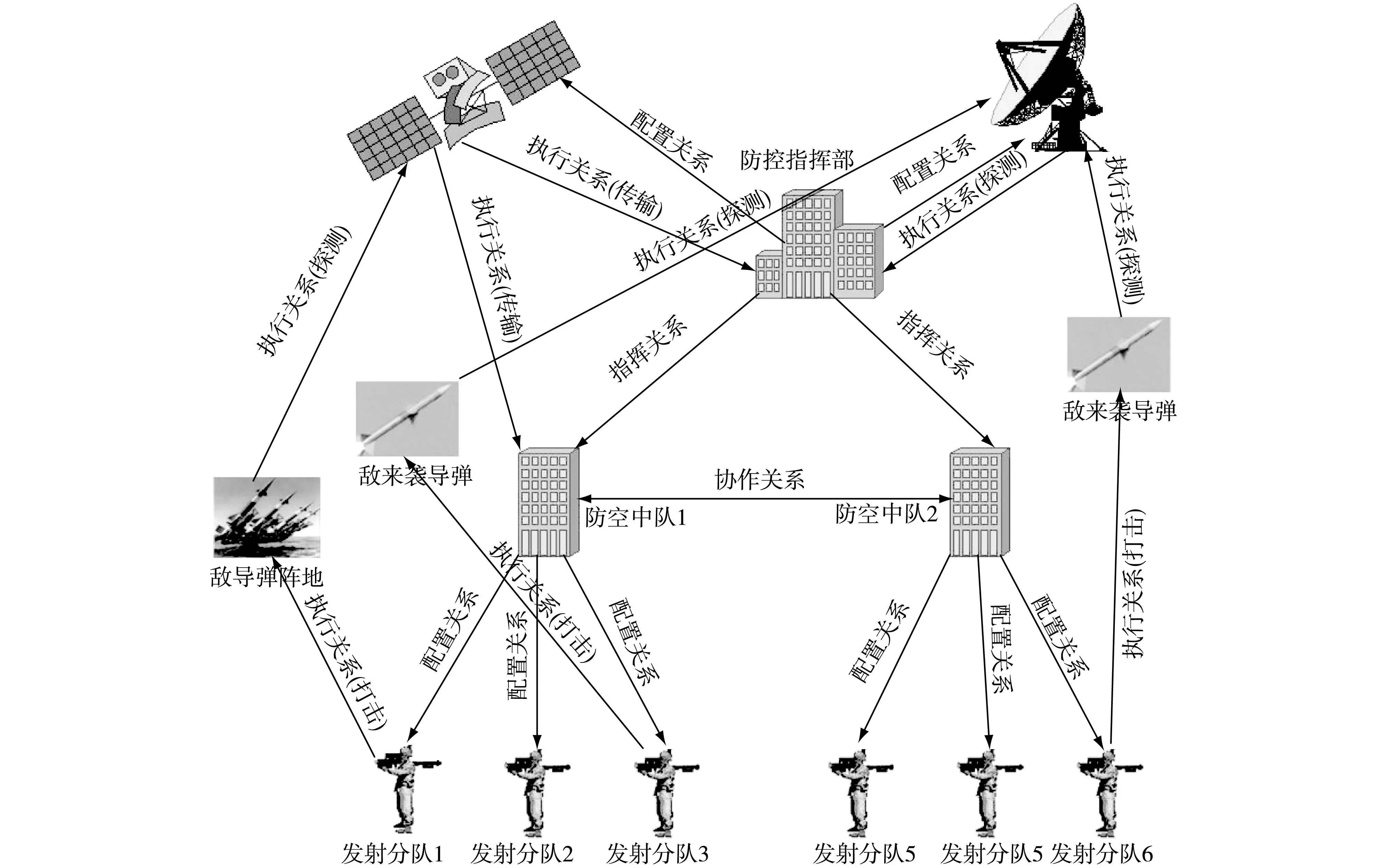
图2　某防空想定指挥控制图

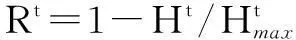
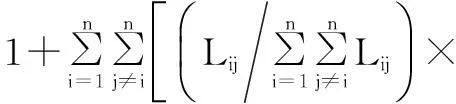
(6)

2.2作战指挥系统组织结构质量有序度模型

(7)

(8)

Ek为系统中指挥联系的跨度数,即联系个数,表示在系统中与第k个元素有直接联系的元素个数,如在图1中与“作战指挥部”直接存在信息来往的有“情报中心”、“通信中心”、“火控中心”、“保障中心”,那么其联系个数就为“4”;Aq为系统质量微观态总数,质量微观态为联系个数与该类元素的个数的乘积。系统总质量熵表示为

(9)

系统最大质量熵:

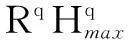
(10)

则该作战指挥系统组织结构质量可表示为

(11)

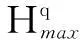
(12)

系统质量越大,表示系统内信息在产生转移时准确性越高,系统的质量有序度越高。

2.3指挥系统组织结构有序度的综合评定

指挥系统组织结构的有序度,要综合考虑其时效和质量两个指标对于系统内不确定性因素的度量。在文献中,将时效与质量的相加取算术平均值,显然这与实际作战指挥需求不相符。特别是在网络空间作战指挥中,情况瞬息万变,战机稍纵即逝;且不同的作战任务要求也不尽相同,所以不能对评价指标一概而论。这里定义系统综合有序度R为

R=αRt+βRq;α+β=1

(13)

α,β为系统中时效和质量的权重系数,根据不同情况对作战指挥系统的要求定义不同的权重系数以得出合理的作战指挥系统有序度。权重系数具体数值可通过专家综合运用层次分析法进行计算得出。

R的数值越大,说明系统有序度和指控效率越高。

3应用实例

3.1情况说明

图3表示基于传统作战指挥系统组织结构建立的网络空间作战指挥系统,其中信息的传递只在各要素及其下属要素间进行,高级平台与次级平台间的信息交流仅限于有直接隶属关系的各要素，所有信息最终汇总于顶层,由顶层完成决策计划、指挥协同，属于典型的顶层设计、部门分工合作式的指挥控制系统。图中“①”表示第1种元素的标号序号,与下图含义相同。

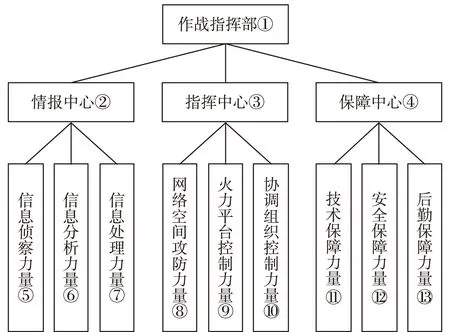
图3　传统型网络空间作战指挥系统组织结构示意图

图4在原有基础上,加强了相邻层级间的信息交流,使上级平台的信息能够与所有次级平台要素共享,增加了信息向下传达和向上反馈的通信链路。如信息侦查组获取通信遭到干扰的信息需将此信息传递至通信保障组,在传统型系统中需经过作战指挥部再转达至信息保障组;在改进型系统中信息侦查组可将信息同时向作战指挥部和通信保障组传递,提高了指挥的效率。这种系统拓扑结构能够充分体现出网络空间作战信息高度的互联互通,同时多通信链路的存在能够增强指挥系统的抗毁性能。亦可以理解为网络空间作战任务非单一作战单元能够完成,需要参战各要素共享信息,协力完成同一作战目标。

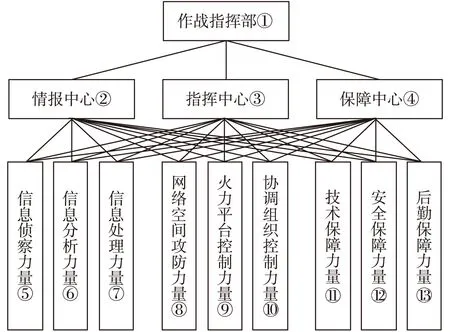
图4　改进型网络空间作战指挥系统结构组织示意图

3.2模型计算

根据上述系统有序度计算步骤,对以上两种组织结构的时效熵和质量熵进行计算，结果如表1-5所示。

表1　传统型作战指挥系统时效熵

表2　传统型作战指挥系统质量熵

表3　改进型作战指挥系统时效熵

表4　改进型作战指挥系统质量熵

计算过程如下:

在此实例中,改进型系统组织结构的时效熵与质量熵均较传统型作战指挥系统组织结构有所提高,为方便计算,取权重系数各为0.5。

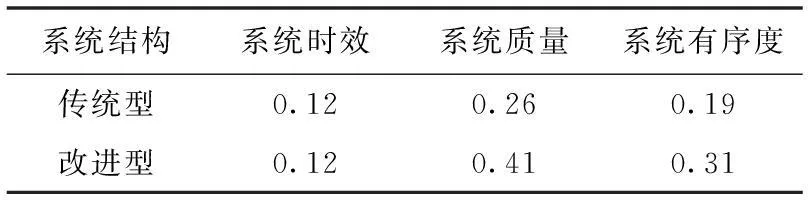
表5　各系统综合有序度

3.3结果分析

在文献[8]中分析了线性指挥系统和扁平式指挥系统的结构有序度,得出系统时效和质量不可兼得的论断。但在实际指挥体系中,单纯的线性结构存在甚微,即使是传统的作战指挥系统,也存在部门间的相互协同。在文献[5,7]构建的指挥系统中,存在系统时效与质量不可得兼的情况,在这种情况下需对权重系数进行讨论分析。根据作战任务的不同,及时性和准确度亦有所偏倚。即使是同一系统,对其的系统组织结构有序的界定也不是固定的,根据不同的作战条件权重会跟随变化,以满足作战指挥的需求。

通过计算所得数据,当作战指挥系统的信息传递链路增加时,信息传递的途径得以增加,系统由金字塔形趋近于扁平型。在时效上没有明显的改变,在质量上取得较大幅度的提高。这说明,在不改变指挥层级而增加指挥信息传递链路,将作战指挥系统结构趋近于扁平时,指挥系统的综合效能得到了提高。这也符合网络空间作战指挥系统的建立高度依赖于信息的互联互通,信息传递渠道的广泛深入也是网络空间作战指挥的必然需求。

4结束语

运用熵理论对传统型和改进型网络空间作战指挥系统组织结构进行定量分析,在时效和质量两个方面对系统进行评定,建立有序度模型,对计算结果进行分析,提出了优化后的扁平式多链路组网模式更适用于网络空间作战指挥系统的构建。同时,影响作战指挥效益的因素还有很多,这里的分析还不够完整全面,后续还将结合更多影响因素对网络空间作战指挥系统的构建进行更加深入的论证分析。

参考文献:

[1]丁邦宇.作战指挥学[M].北京:军事科学出版社,2004.

[2]王刚.任清华. 赛博空间指挥控制问题研究[J].中国电子科学研究院学报,2011(3):243-246.

[3]孙儒凌.作战指挥基础理论[M].北京:国防大学出版社,2011.

[4]邱菀华.熵学及其近代应用[M].北京:北京航空航天大学,1993:33-40.

[5]蒋胜平,汪清园.基于结构熵模型的炮兵致使体制评价方法[J].舰船电子工程,2012(6):23-24.

[6]来 源,季福新,毕长剑.基于结构熵模型的指挥控制系统组织结构评价[J].系统工程,2001(4):27-31.

[7]解维河,汪德虎.基于熵理论的舰炮作战指挥方式[J].四川兵工学报,2014 (12):28-30.

[8]庄钟锐,黄文伟,于淼.基于熵理论的指挥系统拓扑结构有序度评价分析[J].火力与指挥控制,2010(6):73-75.

[9]付新华,张伟星,付新兵.基于熵理论的航空兵作战指挥体系建模分析[J].空军空降兵学院学报,2014(1):26-29.

[10]张东戈,C3I系统评估中信息效用概念的提出[J].系统工程与电子技术, 2001, 23(6):46-48.

[11]Zhang Dongge, Study on information utility[J].Journal of Systems Engineering and Electronics, 2005,16(3): 579-582.

[12]周道安，张东戈，常树春.C2组织指挥控制关系的形式化描述[J].指挥控制与仿真，2008，30(4)：13-17,40.

Cyberspace Combat Command System StructureOptimization Based on Entropy Theory

WANG Nan-xing, WANG Jin-song, LI Guo-wei

(PLA Information Engineering University, Zhengzhou 450001, China)

Abstract:The quality of the combat command system is usually judged by the timeliness and the accuracy of the information transformation in the system. These two items can be effectively analyzed quantitatively with the measurements of timeliness and quality in structure entropy theory. Using structure entropy theory, this paper builds up system order degree models for the traditional and the improved constructions of cyberspace combat command system. Then, the models are analyzed using some examples to find out the relevant effectiveness of these two combat command systems so as to assist the construction of the cyberspace combat command system.

Key words:entropy theory； cyberspace； combat command； order degree； optimization

作者简介：王南星(1988-),男,河南郑州人，硕士研究生,研究方向为信息作战指挥理论与应用,

*基金项目：全军军事类研究生资助课题(2014JY168)

收稿日期：2015-11-04

中图分类号:E94

文献标志码:A

DOI:10.3969/j.issn.1673-3819.2016.01.004

文章编号：1673-3819(2016)01-0013-05