一类具有时滞的传染病模型的Hopf分支分析

陶　龙，曹　磊，周　文，张道祥

(安徽师范大学数学计算机科学学院, 安徽 芜湖 241000)



一类具有时滞的传染病模型的Hopf分支分析

陶龙，曹磊，周文，张道祥

(安徽师范大学数学计算机科学学院, 安徽 芜湖 241000)

摘要：考虑体检和消除疾病因素的影响，提出并研究了一类具有潜伏时滞的SEIR模型.得到了正平衡点局部稳定的以及发生Hopf分支的充分条件.进一步地,利用规范形理论和中心流形定理获得Hopf分支的特性,如分支方向和稳定性.所得结果改进和扩展了文献中的相应结果.

关键词：SEIR疾病模型;时滞;稳定性;Hopf分支;周期解

0引言

数学模型中微分方程动力系统在理解疾病传送机制对人口水平影响方面扮演着重要的角色[1-7].而国内外学者产生兴趣的重要课题之一是模型由于时滞产生Hopf分支进而导致周期解.

文[3-5]考虑了具有暂时免疫性的传染病模型,研究了系统稳定性并得到Hopf分支参数曲线.文[6]考虑了具有非线性发生率和恢复期时滞的SIS模型,并给出了系统在地方性平衡点产生Hopf分支的充分条件.文[7]研究了具有时滞和不同潜伏期的艾滋病模型,讨论了时滞影响疾病平衡点的稳定性及分支现象.随着医疗条件的改善,人类的某些疾病可以通过体检等手段来发现,此时通过治疗从而延缓或避免自己成为疾病的传播源[8]；再者,计算机蠕虫病毒由于受到杀毒软件的检测和清除病毒的影响,其潜伏者类E的变化率也有可能与时滞有关.如文[8]研究了具有双线性发生率和潜伏期时滞的SEIDQV计算机蠕虫病毒模型,得到系统的Hopf现象,并提出了控制病毒传播的隔离策略，基于此研究更具有实际意义.本文考虑了如下一类具有瞬时免疫,并且在潜伏期受体检和清除疾病影响而带有时滞的SEIR模型.

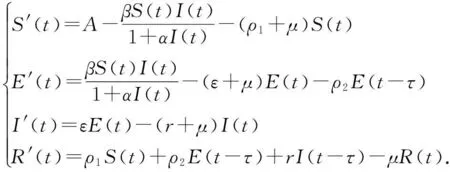
(1)

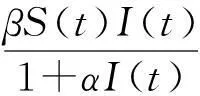
注意到上式中的前三个方程与R无关,所以只需要考虑如下系统:

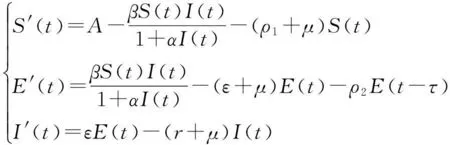
(2)

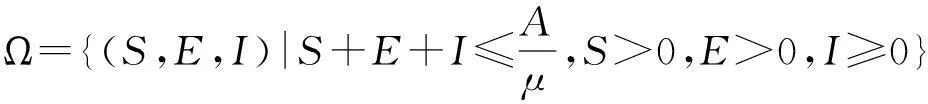
(3)

1平衡点的局部稳定性和Hopf分支的存在性

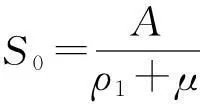
H(1):R0>1

在H(1)的条件下系统存在地方病平衡点P*(S*,E*,I*),其中

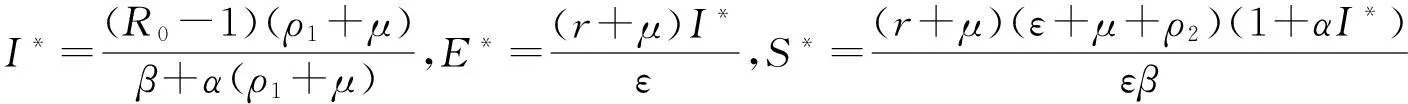
其中

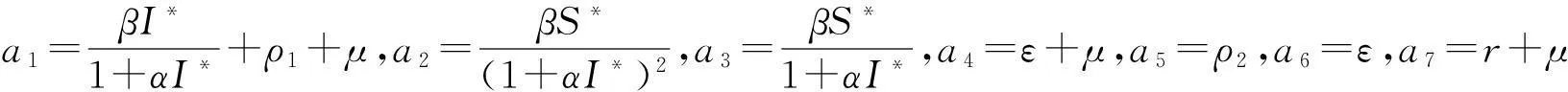
从而其特征方程为

λ3+A1λ2+A2λ+A3+e-λτ(B1λ2+B2λ+B3)=0.

(4)

其中

A1=a1+a4+a7,A2=a1a4+a1a7+a4a7-a2a6,A3=a1a4a7+a2a3a6-a1a2a6,

B1=a5,B2=a1a5+a5a7,B3=a1a5a7

当τ=0时此时的特征方程为

λ3+(A1+B1)λ2+(A2+B2)λ+A3+B3=0

(5)

H(2):

A1+B2>0

(A1+B1)(A2+B2)-(A3+B3)>0

易知当H(2)满足时,由Routh-Huritz[10]定理可知当τ=0时平衡点P*是局部渐近稳定的.

若λ=iω是特征方程(4)的根,将其实虚部分开,则有:

B2ωsin(ωτ)+(B3-B1ω2)cos(ωτ)=A1ω2-A3;

B2ωcos(ωτ)-(B3-B1ω2)sin(ωτ)=ω3-A-2ω

(6)

对上述两个方程同时平方后相加得

ω6+r1ω4+r2ω2+r3=0

(7)

其中

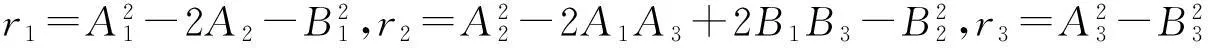
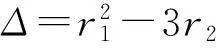
h(z)=z3+r1z2+r2z+r3=0

(8)

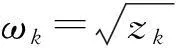
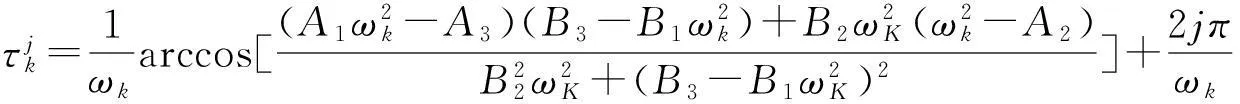
(9)

使得方程有一对纯虚根±iωk.

定义:

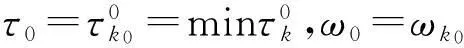
(10)

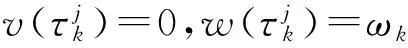
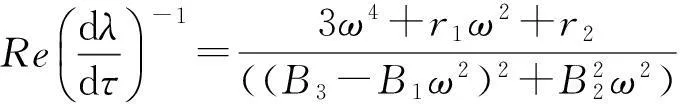
(11)

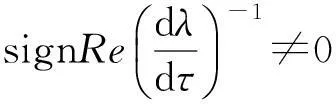
综上所述:

定理1若满足H(1)和H(2)的条件则

(1)当r3>0且Δ≤0时地方病平衡点P*是渐近稳定的.

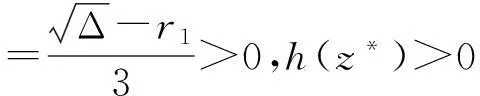
2Hopf分支方向和稳定性分析

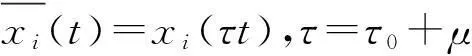
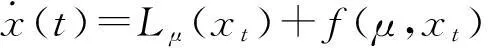
(12)

其中x(t)=(x1(t),x2(t),x3(t))T∈R3,Lμ:C→R,f:R×C→R.Lμ,f的表达式为:

Lμφ=[B1φ(0)+B2φ(-1)]

(13)

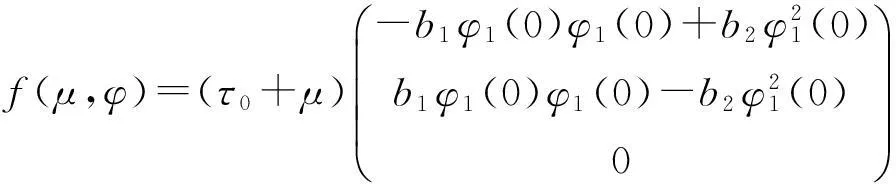
(14)

其中

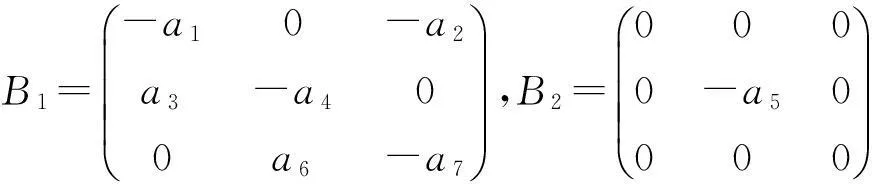
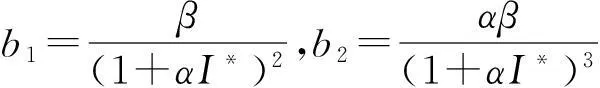
利用Riesz表现定理,存在一个在θ∈[-1,0]上的有界变差函数η(θ,μ)使得

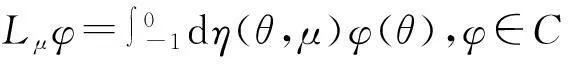
(15)

事实上可以选择

η(θ,μ)=(τ0+μ)[B1δ(θ)+B2δ(θ+1)]

(16)

其中δ(θ)是Dirac-δ-函数.

接下来,对φ∈C1([-1,0],R3)定义如下算子:

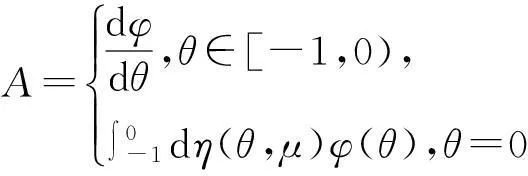
(17)

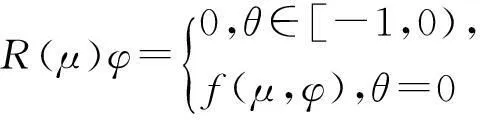
(18)

从而系统(12)等价为:

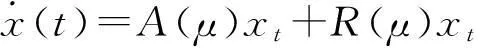
(19)

其中xt(θ)=x(t+θ),θ∈[-1,0].

当ψ∈C1([-1,0],(R3)*)定义A的共轭算子A*为

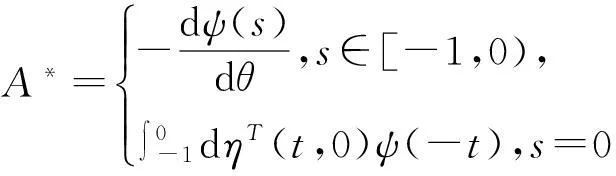
(20)

对φ∈C1[-1,0]和ψ∈C1[-1,0]定义双线性映射:

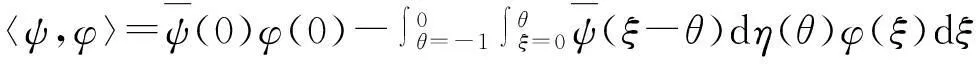
(21)

当η(θ)=η(θ,0)有±iτ0ω0是A(0)的特征值,再由共轭算子的性质知±iτ0ω0也是A*(0)的特征值.

下面分别计算出A(0)和A*(0)对应τ0ω0和-τ0ω0的特征向量.设q(θ)=(1,m,n)eiτ0ω0θ为A(0)对应于iτ0ω0的特征向量,从而易知

A(0)q(θ)=iτ0ω0q(θ)

(22)

从而由A(0)的定义和式(13)(15)(16)得:

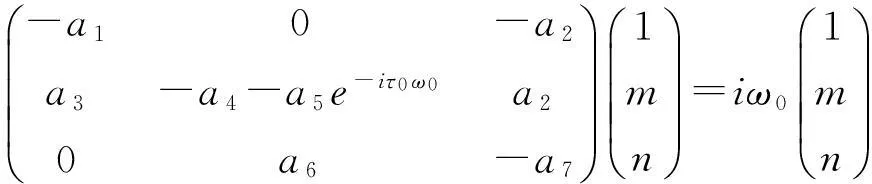
(23)

所以有

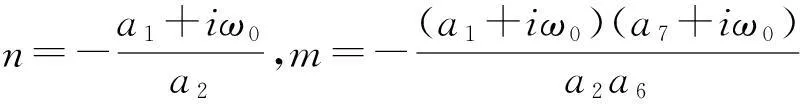
同理令q*(θ)=M(1,m*,n*)eiτ0ω0θ是A*(0)关于-iτ0ω0的特征向量,从而由A*(0)的定义和式(13),(15)得

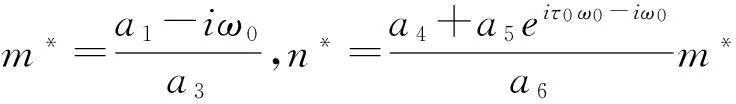
为了保证〈q*,q〉=1,很容易计算出M.由式(21)易得:

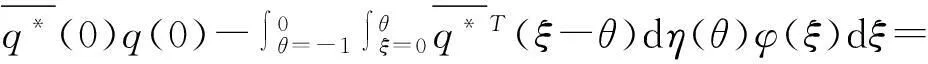
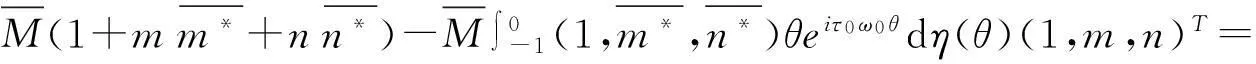
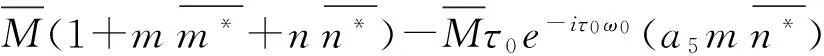
(24)

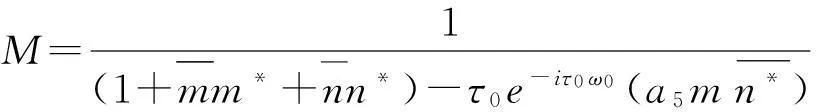
接下来利用和Hassard[11]类似的方法,先计算中心流形C0的状态坐标.当μ=0时,令xt是(19)在μ=0时的解.定义:

z(t)=〈q*,xt〉,W(t,θ)=xt-2Rez(t)q(θ)

(25)

从而在中心流形C0处有:

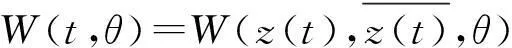
(26)

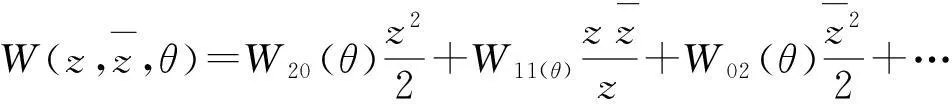
(27)

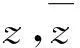
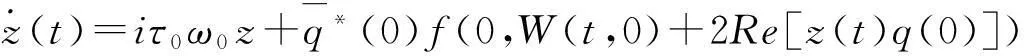
(28)

即

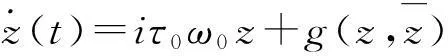
(29)

其中

(30)

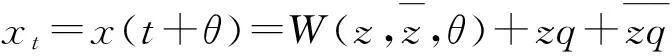
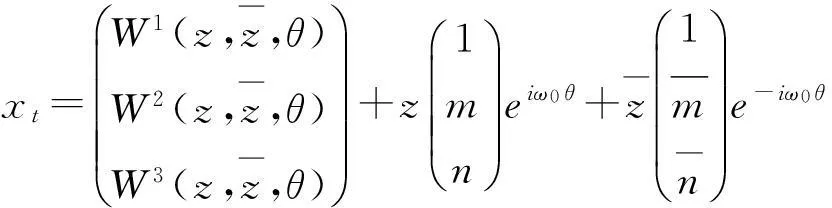
(31)

从而

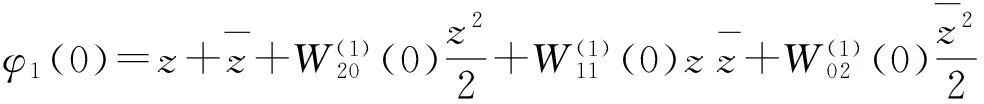
(32)

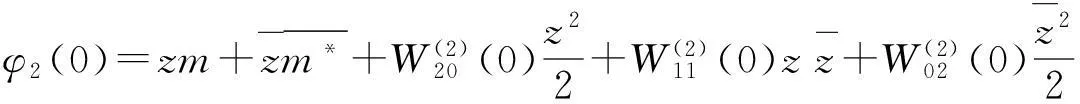
(33)

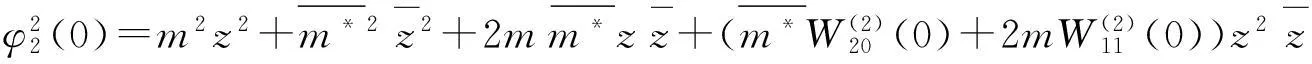
(34)

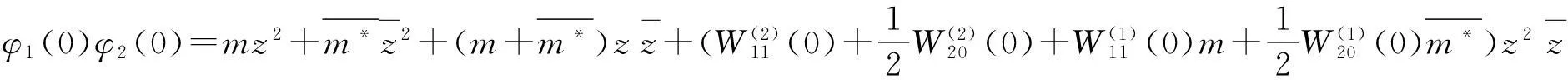
(35)

由(28)和(29)得:

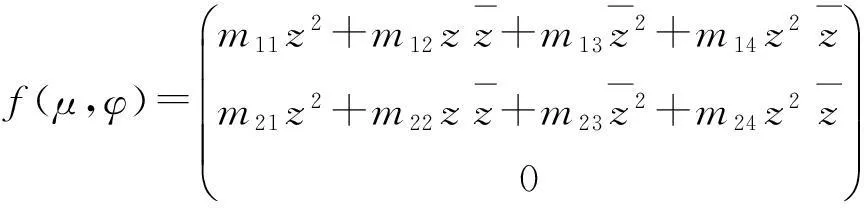
(36)

其中

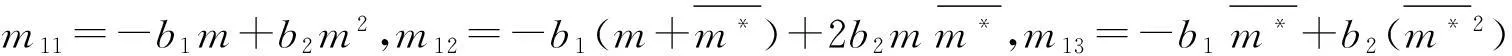
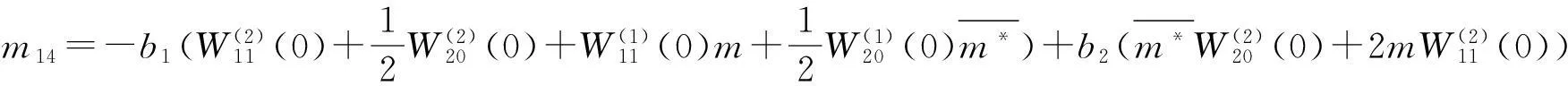
m21=-m11,m22=-m12,m23=m13,m24=m14

由于有:

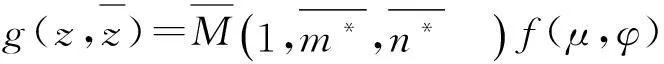
比较式(30)得出:

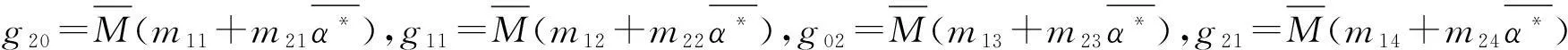
由于在g21中用到了W20(θ)和W11(θ),接下来计算它们的值.由式(19)和(25)知:

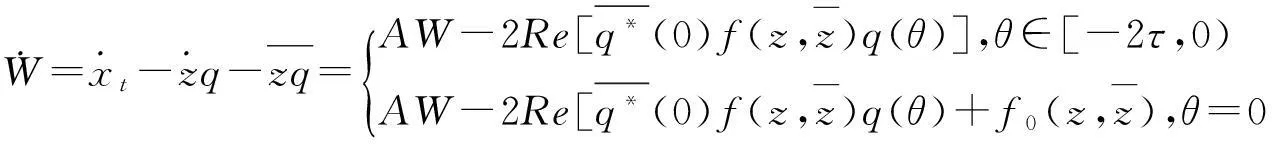
(37)

令

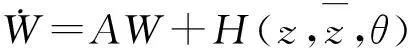
(38)

其中

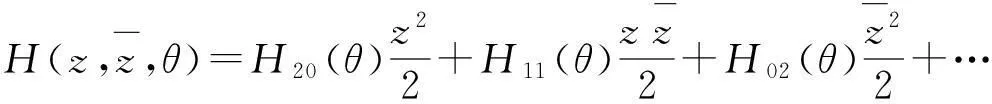
(39)

将式(37)带入(38)并比较系数有:

(A-2iω0)W20(θ)=-H20(θ),AW11(θ)=-H11(θ),(A+2iω0)W02(θ)=-H02(θ)

(40)

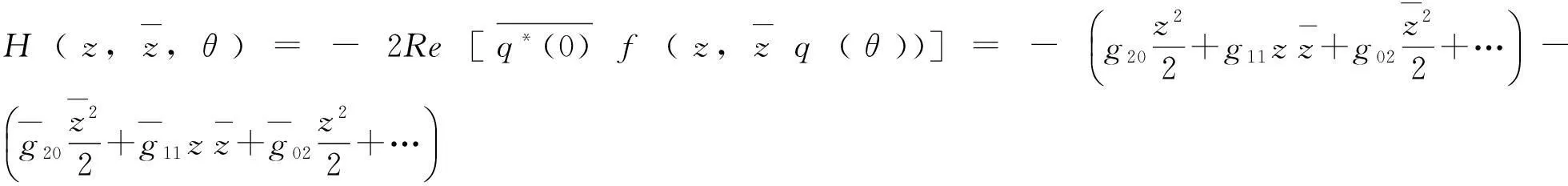
从而：

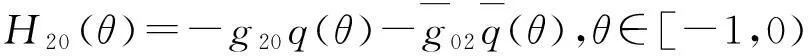
(41)

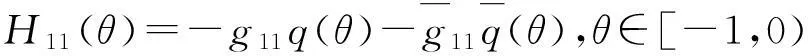
(42)

由式(40)(41)(42)得:

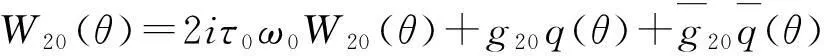
(43)

(44)

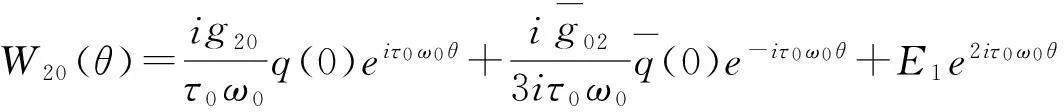
(45)

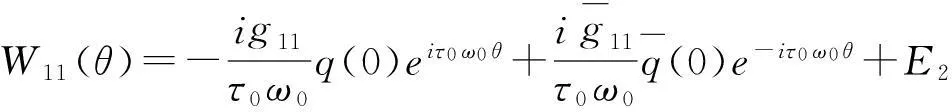
(46)

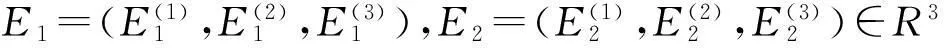
接下来计算E1,E2.由式(40)有

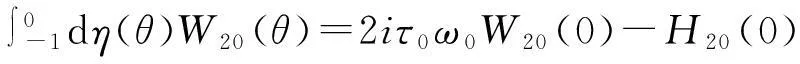
(47)

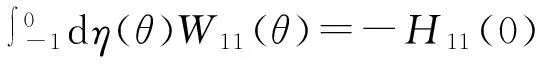
(48)

从式(37)得:

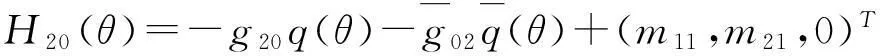
(49)

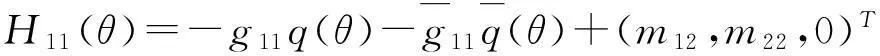
(50)

注意到:

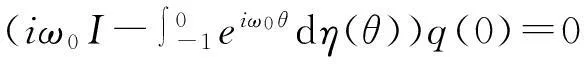
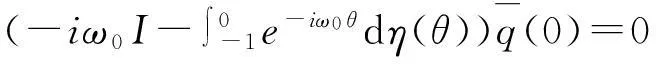
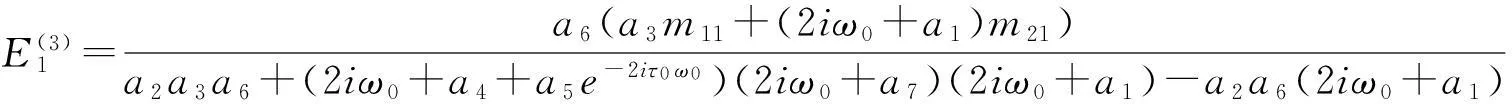
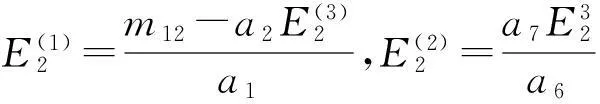
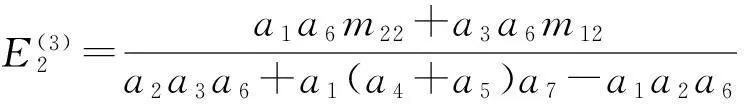
进而有

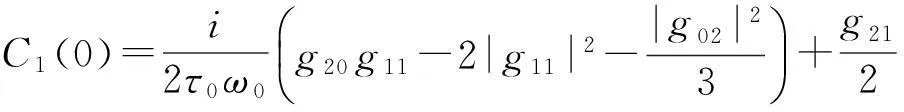
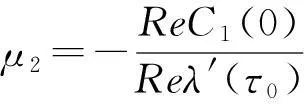
β2=2ReC1(0)

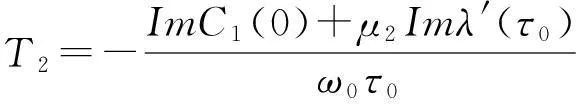
定理2在上述的情况下有以下结论:

1)μ2的正负决定了Hopf分支的方向,当μ2>0(μ2<0)时Hopf分支是向前分支(向后分支),此时分支周期解是存在的当且仅当τ>τ0(τ<τ0);

2)β2的正负决定了分支周期解的稳定性,当β2<0(β2>0)分支周期解是稳定的(不稳定);

3)T2的正负决定了分支周期解的周期,当T2>0(T2<0)周期是递增(递减)的.

参考文献:

[1] 赵金庆,刘茂省,马扬军,等.带有双噪音的随机SI传染病模型的稳定性与分岔[J].应用数学和力学,2013,34(12):1300-1310.

[2] ZHANG Daoxiang, DING Weiwei, ZHU Min. Existence of positive periodic solutions of competitor-competitor-mutualist Lotka-Volterra systems with infinite delays[J]. Journal of Systems Science and Complexity, 2015, 28(2)：316-326.

[3] 尹红云,董冉冉,张道祥.一类具有饱和发病率与暂时免疫的时滞SIRS模型[J].安徽师范大学学报(自然科学版),2012,35(2):115-118.

[4] 宋蛰,李海春,陶桂洪.一类具有暂时免疫传染病模型的Hopf分支[J].生物数学学报,2009,24(3):427-432.

[5] 童姗姗,窦霁虹,王佳颖.一类具时滞和非线性传染率的SIS传染病模型的Hopf分支[J].延安大学学报(自然科学版),2011,30(3):19-21.

[6] AGARMAL M, VERMA V. Stability and Hopf bifurcation analysis of a SIRS Epidemic model with time Delay[J]. International Journal of Applied Mathematics and Mechanics, 2012, 8(9):1-16.

[7] 尹锦锦,胡志兴.具有时滞和不同潜伏阶段的艾滋病模型的Hopf分支[J].陕西师范大学学报(自然科学版),2014,42(5):6-11.

[8] YAO Yu, XIANG Wenlong, QU Andong, et al. Hopf bifurcation in an SEIDQV worm propagation model with quarantine strategy[J]. Discrete Dynamics in Nature and Society,2012,2012:1-8.

[9] CAPSSSO V, SERIO G. A generalization of the kermack-Mckendrick deterministic epidemic model[J]. Mathematical Biosciences, 1978,42(1):43-61.

[10] OLGA Holtz. Hermite-Biehler, Routh-Hurwitz, and total positivity[J]. Linear Algebra and its Applications, 2003, 372:105-110.

[11] HASSARE B D, KAZZRINOFF N D, WAN Y N. Theory and applications of Hopf bifurcation[M]. Cambridge: Cambridge University Press, 1981:129-144.

第15卷第1期2016年1月杭州师范大学学报(自然科学版)JournalofHangzhouNormalUniversity(NaturalScienceEdition)Vol.15No.1Jan.2016

Hopf Bifurcation of a Class of Delayed Epidemic Model

TAO Long, CAO Lei, ZHOU Wen, ZHANG Daoxiang

(College of Mathematics and Computer Science, Anhui Normal University, Wuhu 241000, China)

Abstract:Considering the impact of health examination and removing infectious diseases, a new delayed SEIR model is proposed and investigated. Sufficient conditions for the local stability of the positive equilibrium and the existence of Hopf bifurcation are obtained. Further, the properties of Hopf bifurcation, such as the direction and stability, are investigated by using the normal form theory and center manifold argument. The results of references are improved and extended.

Key words:SEIR epidemic model; delays; stability; Hopf bifurcation; periodic solution

文章编号:1674-232X(2016)01-0081-07

中图分类号:O175.14MSC2010: 92D30

文献标志码:A

doi:10.3969/j.issn.1674-232X.2016.01.016

通信作者：张道祥(1979—)，男，副教授，博士，主要从事微分方程理论及应用研究.E-mail:18955302433@163.com.

基金项目：国家自然科学基金项目(11302002).

收稿日期：2015-05-21