基于改进神经网络的两电机同步系统张力辨识

袁 骏，刘国海

(江苏大学，镇江 212013)

基于改进神经网络的两电机同步系统张力辨识

袁 骏，刘国海

(江苏大学，镇江 212013)

张力辨识是实现两电机同步系统无传感器运行的重要步骤。为了辨识出张力值，在系统数学模型左逆存在性已证明的前提下，针对BP算法训练慢且精度不高，两电机系统存在负载扰动和系统噪声的特点，提出一种基于跟踪微分器——粒子群优化BP网络左逆软测量辨识方法。仿真结果表明，该方法辨识出的张力可以在存在负载扰动情况下精确跟踪张力实际值，抑制外在扰动对于张力辨识的影响，为实现两电机无张力传感器系统的控制提供了现实可行性。

两电机同步系统；张力辨识；神经网络左逆；跟踪微分器；粒子群算法

0 引 言

多电机同步系统广泛应用于各工业领域，比如轨道交通、电动汽车以及冶金业等[1-4]。对于由两个三相交流感应电机组成的两电机同步系统而言，它具有多变量、非线性、强耦合和时变的特性[5]，而且在实际运行中，易受外在扰动和负载变化的影响。在两电机同步系统运行过程中，皮带的张力和运行的速度是否被同步控制是系统安全运行的关键。皮带的滚轴由电机拖动旋转来控制皮带张力，若张力传感器发生故障，错误测量，可能会使皮带撕裂，最终导致整个系统崩溃。因此，张力控制是保证物料运输质量和效率的重要环节。为达到系统张力控制的精度要求，就必须对皮带张力进行精确地实时监控。如今大多类似系统中，都在系统内部安装传感器来检测张力，但张力传感器本身精度不高、价格不菲、且信号在噪声干扰下存在延迟现象[6]，这无疑使得张力传感器的进一步应用受到了限制。

长期以来，张力的辨识工作得到众多专家学者的关注与探究，这些探究均基于精确系统模型，且系统运行会存在一定的外界扰动，需要对系统参数进行实时监控并调整，使得辨识效果滞后，精度降低。两电机系统的特性决定了其数学模型十分复杂，且系统工作环境恶劣，因此需要探究出一种不基于系统数学模型的辨识方法尤为重要。近几年东南大学戴先中教授与王万成博士提出一种利用神经网络逼近函数特性来实现对参数的跟踪与辨识[7-8]，称为神经网络左逆软测量。本文利用粒子群算法(Particle Swarm Optimization，PSO)的快速性以及微分跟踪器(Tracking Differentiator，TD)的强抗干扰力，提出了改进神经网络左逆软测量的方法，即基于TD-PSOBP的张力左逆辨识策略，使神经网络训练速度大幅加快，进一步提高张力辨识的精度；减少系统内外干扰引起的误差，具有较强的鲁棒性。本文以两电机同步系统为例，通过搭建系统仿真模型，分别在负载恒定和负载突变运行环境下，完成对张力值的辨识并进行比较，验证该方法的可行性。

1 两电机数学模型及左逆可逆性分析

1.1 两电机同步系统数学模型

图1为两电机系统的物理模型，控制器通过分别传输控制信号给两台变频器来完成对两台三相交流感应电机的控制，电机轴通过一条聚酯皮带连接，当主电机运行时，电机转子运动带动皮带运动，从而完成两电机协调运动。

图1 两电机同步系统的物理模型

在两电机同步系统中，当变频器采用矢量控制运行模式运行时，考虑转子磁链恒定，其数学模型：

式中：ωi和ωri分别代表电机的同步角速度和电气角速度；npi,Ji,ψri分别表示电机的极对数，转动惯量和转子磁链；Lri,Tri,TLi分别为电机的转子自感，电磁时间常数以及负载转矩；ri,ki为电机的半径和速比(i=1, 2)；F为皮带张力；K=E/V表示传递系数，其中E表示传动带的杨氏弹性模量，V表示期望速度；T=L0/AV为张力变化时间常数，L0表示机架间距离。

1.2 左逆系统的证明与搭建

根据式(1)，其中：

输出:

y=h(x)=[y1,y2]T=[x1,x3]T=[ωr1,F]T

控制变量:

u=[u1,u2]T=[ω1,ω2]T

状态变量:

x=[x1,x2,x3]T=[ωr1,ωr2,F]T

于是，式(1)又可被表示:

(2)

为了估计出皮带张力x3，假定在两电机同步系统中存在这样一个子系统：系统的输出是可直接测量量x1和x2，输入则是不可直接测量量x3，一些系统参数比如u1,u2是子系统的可变参数。这个子系统被看作是一个“内含传感器”，如图2所示。

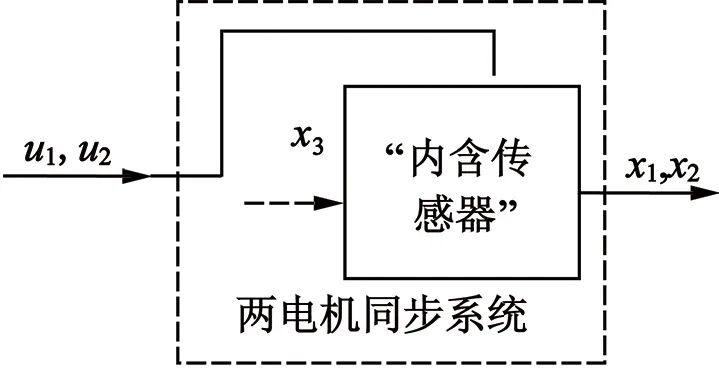
图2 “内含传感器”模型

根据左逆软测量理论，本文将F作为待测变量，选取直接可测变量ωr1，根据“内含传感器”辅助算法[9]对第一台电机转速ωr1进行求导运算，可得：

(3)

得出的相应的Jacobi矩阵为：

(4)

(5)

Jacobi矩阵的秩与待测变量个数相等，则建模算法结束，张力“内含传感器”构造成功，为：

(6)

显然，系统的左逆存在，且左逆系统可被表示为：

(7)

式中：z代表其余可测参数。

根据式所示“内含传感器”左逆表达式。基于“内含传感器”的左逆软测量结构如图3所示。

图3 基于“内含传感器”的左逆软测量模型

2 张力TD-PSOBP左逆辨识

2.1 PSOBP优化算法

作为一种全局搜索的优化算法的PSO算法，响应速度快，需要调整参数少。在该算法中，把解空间的每个潜在解看作一个粒子。所有粒子都有记忆能力，能记忆当前位置、速度以及适应度值。在算法开始前，每个粒子都会初始化其速度和位置，粒子的飞行速度由该粒子自身达到的最优位置和整个粒子种群达到的最优位置来进行动态调整，逐次搜索得到最后的最优解。PSO算法中各粒子根据式(8)更新自己的速度及位置。

(8)

式中：t为迭代代数；Vi=(Vi1,Vi2,…,ViN)和xi=(xi1,xi2,…,xiN)表示粒子当前的速度和位置；c1,c2为学习因子；pi表示第i个粒子自身达到的最优位置，pg表示所有粒子所达到的最优位置；r1,r2是分布于[0,1]的随机数。

基于梯度下降的BP算法过分依赖于初始权阈值的选择，不可避免地存在收敛速度慢且精度低，容易陷入局部最优等缺陷，因此有必要利用其它算法进行完善BP网络的建模功能。考虑到BP算法的特点以及PSO算法良好的全局寻优能力，在对神经网络训练时，采用PSO算法对BP神经网络的初始权阈值进行优化[10]，称为PSOBP算法。该算法不仅能使网络训练速度变快，还能稳定初始权阈值，使训练精度提高。

PSOBP算法的实现步骤如下：

1) 参数初始化。初始化网络的权阈值后将这些值化为单个的粒子，随机初始化这些粒子的位置和速度；再设置好学习因子c1,c2和随机数r1,r2；

2) 迭代更新。利用式(8)分别更新每个粒子的速度和位置，采用均方差作为粒子的适应度函数，计算出每个粒子的适应度值；

3) 经过迭代更新粒子的位置和速度；找出粒子的个体最优位置和种群最优位置；

4) 将最优位置的值赋给BP算法的初始权阈值并进行网络训练。

2.2 基于TD的左逆辨识方法

神经网络左逆软测量在很多领域有广泛应用，例如生化过程测量、电力系统测量等。但在很多工况恶劣、噪声干扰严重的情况下，左逆辨识所使用的神经网络输入在上述影响下出现振荡，输入的微分信号也会在振荡中被噪声淹没，因此辨识精确度大大降低。为改善上述情况，本文将TD[11]代替原有的传统微分器，与左逆系统结合，利用TD噪声中提取微分信号能力强的特点，分析并处理神经网络的输入信号及其微分信号，保证神经网络输入的精确性。

非线性TD不仅不依赖于目标的状态模型，而且不需要测量噪声特性；能在随机噪声或被污染的信号中有效地提取微分信号，不受干扰影响，相比于传统微分器，有显著的优越性。因此本文采用如下非线性TD，其离散形式：

(9)

式中：fhan(x1,x2,r,h)为快速最优控制综合函数，其算法为：

(10)

式中：v0为输入信号；v1为输入信号的跟踪信号；v2表示跟踪的近似微分信号；h表示能量系数；h0表示滤波因子；r为速度因子；fsg(x,d)为定义区间函数，在区间[-d,d]上取1，其余取0，其表达式如式所示。

(11)

合理选择TD的参数，就可以在噪声及其他外部干扰下合理地提取出输入信号的微分信号，抑制噪声。利用TD将传统的左逆观测器进行改进，由TD代替传统微分器，将改造完成的基于TD的左逆(Tracking Differentiator-Neural Network Left Inversion，TD-NNLI)观测器串联在两电机同步系统之后，构造出左逆辨识模型。

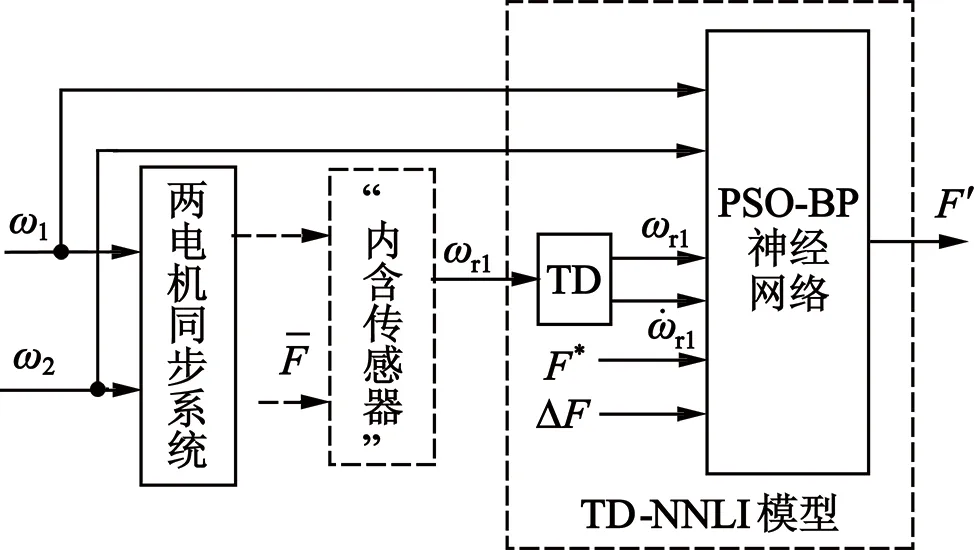
图4 基于TD-PSOBP左逆辨识模型

3 仿真试验

3.1 网络训练

为了验证改进的神经网络左逆软测量系统，在MATLAB中构建两电机同步系统模型。根据实际系统的转速和张力承受范围，给定0～50 kg范围的张力激励，激励采用幅值各不相同的随机方波，使系统能最大化体现其动静态特性，并采集激励张力与采样张力信号，激励张力与采样张力如图5所示。

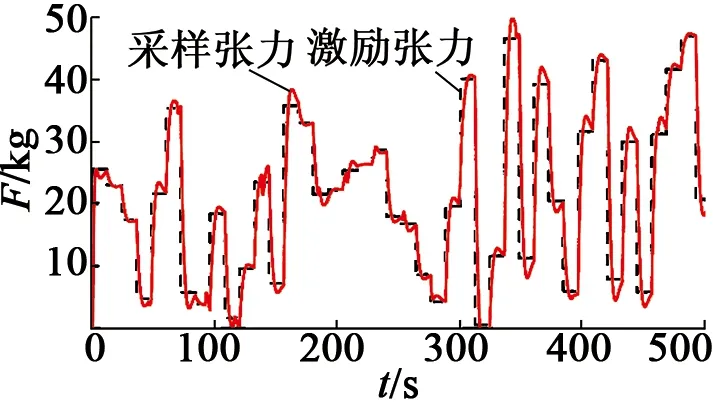
图5 仿真中张力采样数据

为验证TD-PSOBP左逆系统的可行性，利用采样数据分别对传统BP网络和PSOBP网络训练。PSO算法中学习因子c1,c2均设置为1.494 45，迭代次数设置为50次。表1列出了PSOBP网络和传统BP网络的训练精度和步数对比。

表1 训练结果比较

从训练结果可知，PSOBP网络比传统BP网络收敛速度更快，且训练精度大大提高，取得了较好的训练效果。

3.2 仿真

将训练得到的PSOBP网络代入系统模型，串联到两电机同步系统后，得到PSOBP左逆辨识模型。张力F给定上下限为0 kg，35 kg的随机方波。传统BP左逆辨识系统得到的实际张力波形、辨识波形和辨识误差结果如图6；PSOBP左逆辨识系统得到的结果如图7所示。

图6 传统BP左逆辨识仿真结果图7 PSOBP左逆辨识仿真结果

仿真结果表明，PSOBP左逆辨识策略辨识得到的张力比传统BP左逆辨识更好地跟踪了实际值，动态响应更快，尤其表现在实际张力突降时，稳态波形平滑且辨识精度较高，辨识效果较理想。

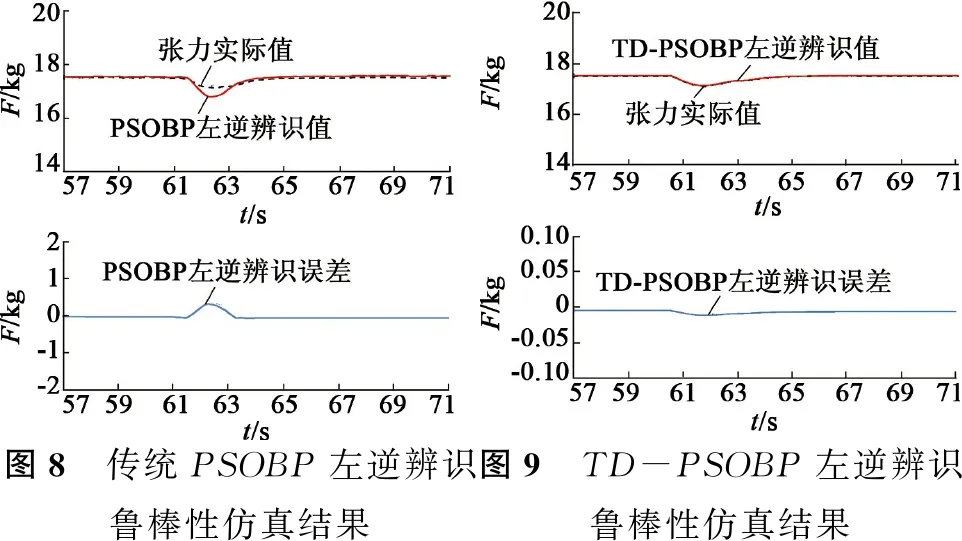
为验证TD-PSOBP张力左逆辨识对负载扰动的鲁棒性，负载转矩在60 s时从15 N·m突降到5 N·m。图8和图9为PSOBP左逆辨识和TD-PSOBP左逆辨识的辨识效果。

通过比较图8和图9的仿真结果可知，存在扰动时，TD-PSOBP左逆辨识的辨识结果响应速度更快，辨识误差能在很短时间内收敛，稳态误差也较传统PSOBP小，鲁棒性能良好。

4 结 语

本文提出了一种在负载突变情况下的TD-PSOBP张力辨识策略，利用基于TD的张力左逆观测器实现对张力的实时观测。通过理论和仿真验证，该策略不仅不依赖系统数学模型，而且训练迅速精确，由于TD的特性使得系统的抗干扰能力大大增强。为工业大规模生产运输节约了张力传感器这一环节的维修费用和使用成本，具有实际意义。

[1] WANG Z，PARANJAPE R.An evaluation of electric vehicle penetration under demand response in a multi-agent based simulation[C]//IEEE Electrical Power and Energy Conference，2014，11：220-225.

[2] 卢东斌，欧阳明高，谷靖，等.电动汽车永磁同步电机最优制动能量回馈控制[J].中国电机工程学报，2013，33(3)：83-92.

[3] 孙飞飞，刘星桥.基于自抗扰的三电机同步系统无速度解耦控制[J].微特电机，2014，42(1)：38-41.

[4] CANDEO A，DUCASSY C.Multiphysics modeling of induction hardening of ring gears for the aerospace industry[J].IEEE Transactions on Magnetics，2011，47(5)：918-921.

[5] 康梅，赵文祥，吉敬华，等.基于GA-RBF神经网络逆的两电机同步控制[J].微特电机，2012，40(8)：53-57.

[6] JACOBINA C B，FREITAS I S.Reduced switch-count six-phase AC motor drive systems without input reactor[J].IEEE Transactions on Industrial Electronics，2008，55(5)：2024-2032.

[7] 李亮亮，何勇，叶海翔.永磁同步电动机神经网络逆系统简化模型的研究[J].微特电机，2010，38(7)：57-60.

[8] 王万成，张媛.神经网络逆软测量方法的拓展及在生物浸出过程中的应用[J].仪器仪表学报，2012，33(3)：661-669.

[9] 戴先中.多变量非线性系统的神经网络逆控制方法[M].北京:科学出版社,2005.

[10] 潘芳，仲伟俊.基于粒子群算法的复杂应急调度建模与仿真[J].统计与决策，2014(21)：18-21.

[11] 韩京清，王伟.非线性跟踪-微分器[J].系统科学与数学，1994，14(2)：177-183.

Tension Identification Based on Improved Neural Network of Two-Motor Synchronous System

YUANJun,LIUGuo-hai

(Jiangsu University，Zhenjiang 212013,China)

Tension detection is a key to achieve sensorless operation of two-motor synchronous system. After proving left-invertibility of mathematical model, to identify the tension of belt, a novel identification based on tracking differentiator particle swarm optimization BP network left-inversion is proposed, considering that the convergence speed of BP network is slow and accuracy is low, two-motor system exit load disturbance and system noise. The simulated result shows that, the tension identified by the method can track the actual value exactly under the load disturbance, and also can restrain the influence of the system noise. The result offers practical feasibility for achieving the control of two-motor synchronous system under sensorless operation.

two-motor synchronous system； tension identification； neural network left-inversion (NNLI)； tracking differentiator (TD)； particle swarm optimization (PSO)

2015-10-10

国家自然科学基金项目(61273154,51577084);江苏省高校自然科学研究重大项目(15KJA470002);江苏省“333工程”科研资助项目(BRA2015302)

史晓娟(1970-)，女，工学博士，教授，主要研究方向为数控技术及自动化装备。

TM346

A

1004-7018(2016)12-0077-04