具有阻尼绕组永磁同步电动机的转子位置辨识方法

邓先明，李绍武，刘 娜

(中国矿业大学，徐州 221116)

具有阻尼绕组永磁同步电动机的转子位置辨识方法

邓先明，李绍武，刘 娜

(中国矿业大学，徐州 221116)

针对永磁同步电动机控制系统中位置传感器安装困难、可靠性低的问题，提出基于单相信号注入的无传感器转子位置辨识方法。分析了具有阻尼绕组永磁同步电动机采用单相信号注入法检测转子位置的原理，即通过注入单相高频或低频信号检测电机的阻抗特性，从而准确计算转子位置角度；再利用直流偏置法鉴别转子永磁体的极性。利用有限元方法对具有阻尼绕组永磁同步电动机的阻抗特性和转子位置关系进行了仿真分析。通过有限元仿真与样机实验验证了基于单相信号注入转子位置辨识方法的可行性，为永磁同步电动机无传感器控制技术的实际应用提供了良好的理论基础。

永磁同步电动机；阻尼绕组；信号注入；转子位置辨识；有限元分析

0 引 言

永磁同步电动机具有较高的效率与功率密度，是实现高效节能型传动系统的重要研究方向[1-2]。在由永磁同步电动机构成的高性能交流调速系统中，为实现闭环控制，需获取准确的转子位置信息；对于矢量控制系统，一旦转子位置估计误差过大，将导致电机起动失败[3-4]。传统位置传感器的安装不仅增加系统体积和成本，而且在一些特殊场合也降低了永磁同步电动机应用的可靠性[5-6]。高频信号注入法采用人为制造高频磁场的方法实现转子位置与转速的估计，追踪的是永磁体磁场的饱和性凸极，不依赖于电机参数，具有较高的估计精度与鲁棒性[7-8]，现已成为实现永磁同步电动机零速与低速情况下无传感器控制的首选[9]。

文献[10]在电机定子侧施加低频旋转电压矢量，通过对响应电流的傅里叶分析计算得到转子的位置和极性信息，该方法不依赖于电机的转子结构，同时在重载条件下也可以使用，缺点是会造成电机的小范围微动。文献[11]与文献[12]通过在定子侧注入低频电流信号并检测其响应来获取位置和转速信息，实现隐极PMSM低速条件下的位置估计，适用性好，但该方法存在动态响应速度较慢的问题。文献[13]采用直接磁链法获取永磁同步电动机转子位置。文献[14]采用低频谐波电流注入法检测定子电压响应来判断转子初始位置。文献[15]对带阻尼绕组的永磁同步电动机进行了研究，设计了阻尼绕组补偿器，较好的补偿了阻尼绕组电流对转子位置估计的影响，提高了估计精度，但同时也增加了一定的复杂性。目前来看，对具有阻尼绕组永磁同步电动机采用低频信号注入估算转子位置的方法还少有文献涉及。本文利用有限元仿真对基于信号注入的具有阻尼绕组永磁同步电动机的转子位置辨识方法进行研究，结合实验证明了该方法的正确性。

1 基于单相信号注入转子位置辨识原理分析

在永磁同步电动机的转子结构中，通常无需安装阻尼绕组。如若要求电动机在低速运行时仍具较高的平稳性，就需要有效地降低其输出转矩波纹，为此需安放阻尼绕组以减少电枢反应磁链的脉动[15]。有阻尼绕组永磁同步电动机的结构如图1所示。

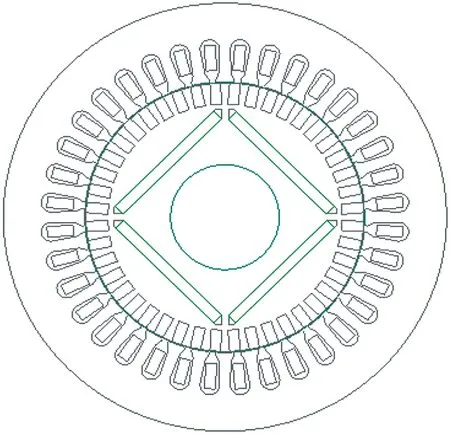
图1 有阻尼绕组永磁同步电动机结构图

1.1 有阻尼绕组永磁电机转子位置检测原理分析

转子有阻尼绕组永磁同步电动机，定子A相单独励磁时等效电路如图2所示。

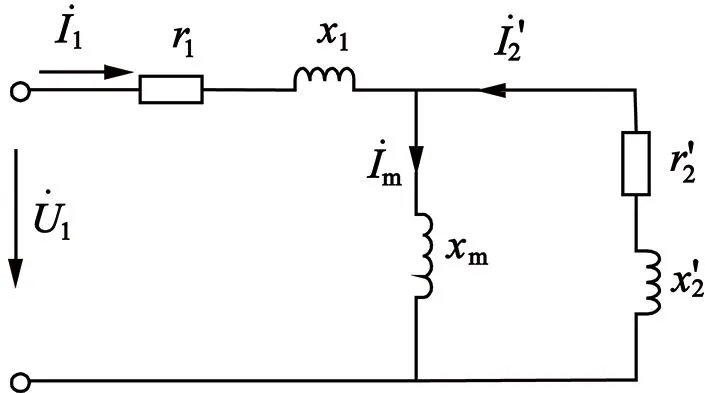
图2 有阻尼绕组永磁同步电动机定子单相励磁时等效电路

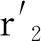
(1)

转子阻尼绕组漏电抗x2的大小与转子漏磁通经过磁路的磁阻R2m成反比，即：

(2)

式中：N1，N2分别表示电枢绕组和转子阻尼绕组的匝数。由式(1)、式(2)可知，当磁阻改变时，其对应的电抗也将发生变化。

1.1.1 高频信号注入法

当定子绕组加单相高频电压时，激磁电抗xm的数值很大，转子阻尼绕组漏电抗相对较小，激磁电抗xm与转子阻尼绕组的漏阻抗并联，激磁电抗支路可等效为断路。因此，永磁同步电动机定子单相高频励磁时等效电路可以简化为图3。

此时，无法利用激磁电抗的变化趋势检测电机的转子位置，定子电流的大小由定转子漏阻抗决定。但是，电机高频漏电抗的大小与转子位置也是密切相关的，可以根据漏电抗的变化趋势检测转子的位置。图4表示A相单独励磁时的转子漏磁场分布情况。由漏电抗变化趋势检测转子位置的原理分析如下。

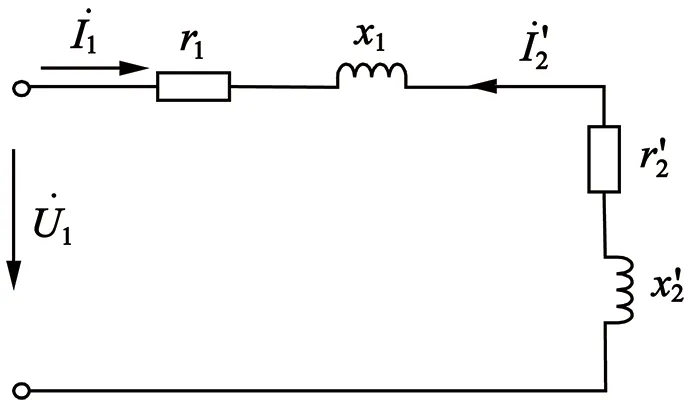
图3 有阻尼绕组永磁同步电定子单相高频励磁时等效电路

图4A相单独励磁转子漏磁场磁力线分布示意图

转子在d，q轴分别形成漏磁回路。由图4(a)可知，当转子d轴与A相的轴线+A轴重合时(定义为转子位置θ=0°处)，转子漏磁通经过转子永磁体外侧的转子铁心构成磁回路，磁阻相对较小，此时转子漏电抗x2较大。由图4(b)当转子q轴靠近+A轴时，转子漏磁通经过的转子铁心截面积越来越小，磁回路经过永磁体，磁阻变大，转子漏电抗x2变小。电机注入高频信号时，可以根据漏电抗的变化趋势检测转子位置角。转子高频漏电抗与转子机械位置角度关系：

(3)

式中：xhσ为最大漏电抗值(d轴)；xlσ为最小漏电抗值(q轴)；θ为转子位置角度。

1.1.2 低频信号注入法

当定子单相加低频电压时，激磁电抗xm的数值较小，而转子阻尼绕组的电阻相对较大，永磁同步电动机定子单相低频励磁时等效电路简化为图5所示，电机低频电抗与转子位置角θ关系：

(4)

式中：xh为低频电抗最大值(q轴)；xl为低频电抗最小值(d轴)。

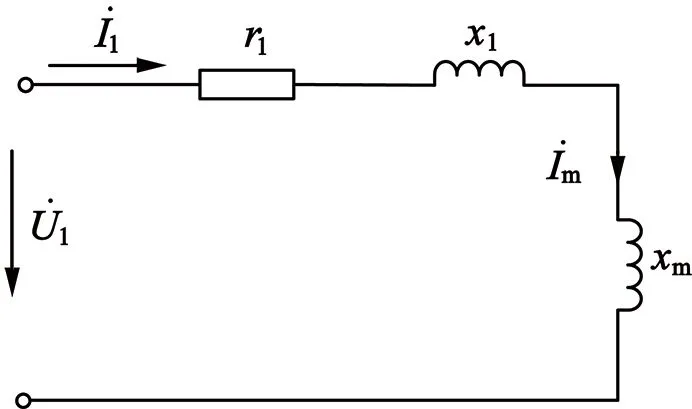
图5 有阻尼绕组永磁同步电动机定子单相低频励磁时等效电路

由于永磁同步电动机的凸极效应，转子d轴存在永磁体，其磁导率与空气相近，磁阻呈最大，电感数值最小；q轴磁阻达到最小，电感数值最大[16]。在电机的定子端注入幅值较小的低频电压(或电流)信号，并通过提取定子绕组中产生的可表征转子位置信息的低频电流(或电压)信号，计算其低频阻抗，利用不同位置的低频电抗值和式(4)可以推导出转子位置和速度信息。

1.2 有阻尼绕组永磁电机的转子极性辨识方法

图6为定子铁心磁化曲线，从图中可以看出磁链与d轴电流的关系。电枢绕组施加直流偏置信号，直流信号形成的磁场与转子磁极方向相同时，绕组磁势起助磁作用，电机磁路饱和程度增加，d轴电感减小；反之，d轴电感变大。改变d轴电流的大小可以改变主磁路的磁链，从而实现对转子永磁体N极的跟踪。

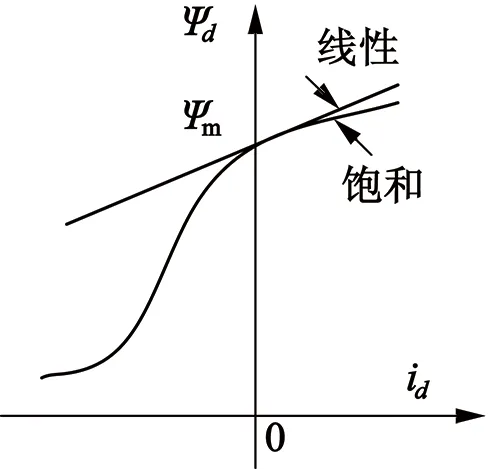
图6 定子铁心磁化曲线

2 转子位置辨识方法的有限元分析

本文仿真及实验采用永磁同步电动机带有阻尼绕组，通过分别注入高频电压和低频电压的方法，对基于单相信号注入的转子位置检测进行有限元分析，并借助叠加直流偏置信号的方法，实现转子永磁体极性的鉴别。

2.1 永磁同步电动机有限元分析模型

本文借助有限元分析法对2对极永磁同步电动机进行仿真，分析其转子位置变化时的高频与低频阻抗特性，仿真模型为带有阻尼绕组的内置式结构电机，其参数见表1所示。

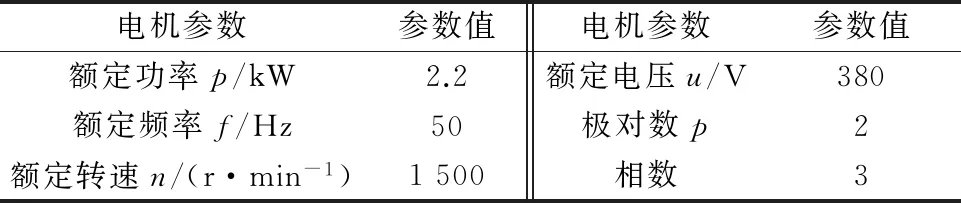
表1 电机参数

2.2 高频信号注入分析

由图7(a)可以看出，当转子机械角度为0°，90°，即转子电角度为0°，180°时，A相电枢绕组轴线与转子d轴位置对齐，漏阻抗最大；当转子电角度为90°，270°时漏阻抗达到最小值。同一转子位置角下漏阻抗的数值随着注入高频电压信号的频率增加而增加。电机的高频漏阻抗主要为感性漏电抗，其大小与频率成正相关，频率越高，漏阻抗数值越大，相应的转子位置辨识精度也就有所提高。有限元仿真结果符合理论分析。

为进一步研究漏阻抗与注入高频电压幅值大小的关系，选用频率为400 Hz，幅值分别为20 V和40 V的电压信号注入AX绕组中，仿真得到电机高频漏阻抗特性如图7(b)所示。

由图7(b)可知，施加电压信号的幅值为20 V和40 V时的漏阻抗曲线基本重合。同一位置角下漏阻抗的数值与注入电压的幅值无关，原因在于漏阻抗与注入信号的频率、磁路的磁阻、绕组匝数有关，与注入信号的幅值无关。因此，注入幅值较小的高频电压信号即可检测出转子的位置。

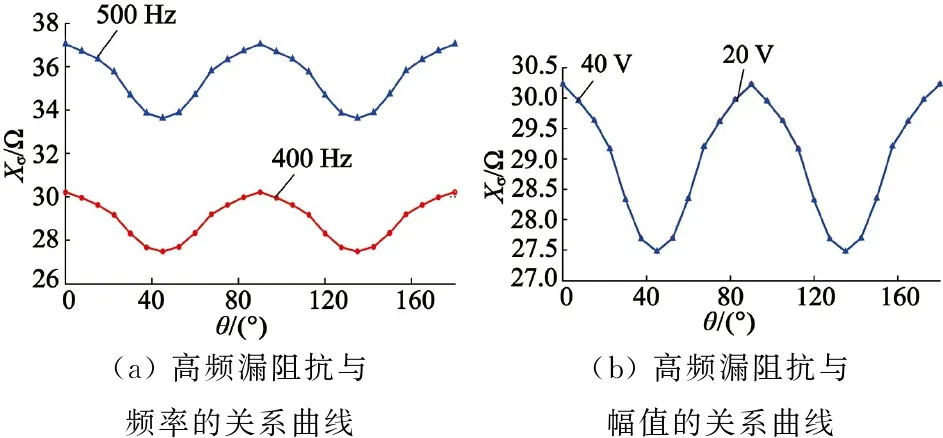
图7 高频漏阻抗与转子位置的关系

2.3 低频信号注入分析

利用有限元方法，在定子端注入低频电压信号实现对电机转子位置的检测。

根据前面的分析，为尽可能地避免单相低频信号注入电机定子时等效电路中阻尼绕组的影响，选用的低频信号的频率f应在合理范围内尽可能取小，否则将无法取得较好的位置检测效果。

小学语文阅读教学中切入点的选择是小学语文教师引导学生剖析、学习一篇文章的着眼点，是阅读教学的起始点。在阅读教学中，教师选择一个恰当合理的切入点，就是选择了文章的突破口，让学生能够举重若轻地把握文章，产生浓厚的学习兴趣和思维的火花。

经过综合考虑后，本文选用幅值均为20 V，频率分别为1 Hz与2 Hz的低频电压信号注入AX绕组，通过检测绕组中产生的电流信号，并计算电压对电流的比值得到低频阻抗的值。鉴于注入的是低频信号，定子绕组中包含的电阻分量不能忽略。有限元仿真得到的低频阻抗特性如图8所示。

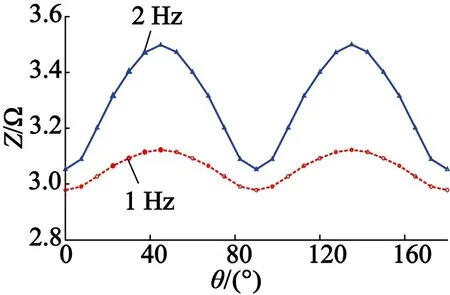
图8 低频阻抗与转子位置的关系

可以看出，在一个电角度周期内，低频阻抗的值与转子位置角度密切相关。当转子机械角度为0°，90°时，磁路处于转子d轴位置，对应的电角度为0°，180°，在此处施加低频电压信号，阻抗最小；转子电角度为90°，270°时，低频阻抗最大。

对比两种频率电压信号注入时电机的低频阻抗发现，频率为1 Hz与2 Hz信号的阻抗特性曲线正弦度都较好，有利于转子位置的检测。但同一位置角下2 Hz信号测得低频阻抗的值更大，原因是信号频率增加，电抗变大，位置辨识精度有所提高。

2.4 转子极性判断

为鉴别转子的极性，首先将电机转子定位于d轴处，在AX绕组中注入低频电压信号，同时在BC-YZ绕组中添加直流偏置信号，根据磁路的饱和原理，即可检测出转子极性。利用有限元方法，选用频率为2 Hz、幅值为20 V的低频电压信号注入AX绕组中，对BC-YZ绕组施加不同幅值的直流偏置信号。图9为BC-YZ绕组中分别叠加-2～2 A直流偏置信号时的低频阻抗特性曲线。

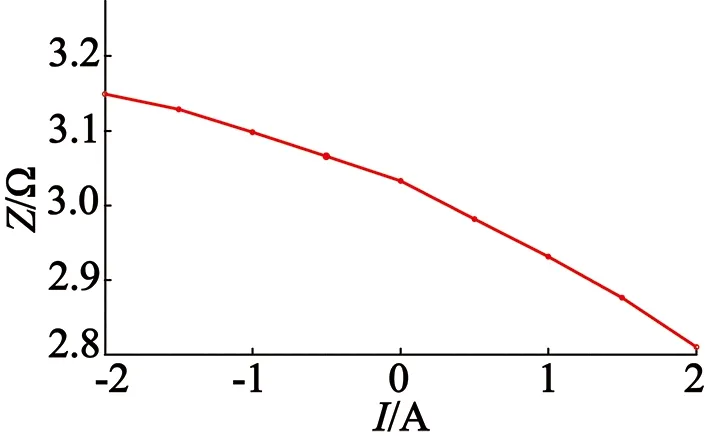
图9 施加直流偏置的低频阻抗特性

根据该仿真结果，当施加直流电流方向为正，绕组磁势起增磁作用，d轴磁路饱和程度增强，低频阻抗减小；相反，低频阻抗随d轴磁路饱和程度的降低而增大。当叠加直流分量的数值越大，d轴磁路饱和程度的变化越明显，阻抗的变化也就越大。有限元仿真结果与理论分析相吻合。

3 样机实验分析

为验证采用单相信号注入法实现有阻尼绕组永磁同步电动机转子位置辨识在实际应用中的可行性，本文运用了如图10所示的实验线路方案。其中样机采用如图11(a)所示带有阻尼绕组的TYBZ系列永磁同步电动机，额定电压380 V，容量2.2 kW，额定电流为4.5 A，频率为50 Hz，额定转速为1 500 r/min, 图11(b)为实验所用控制台。

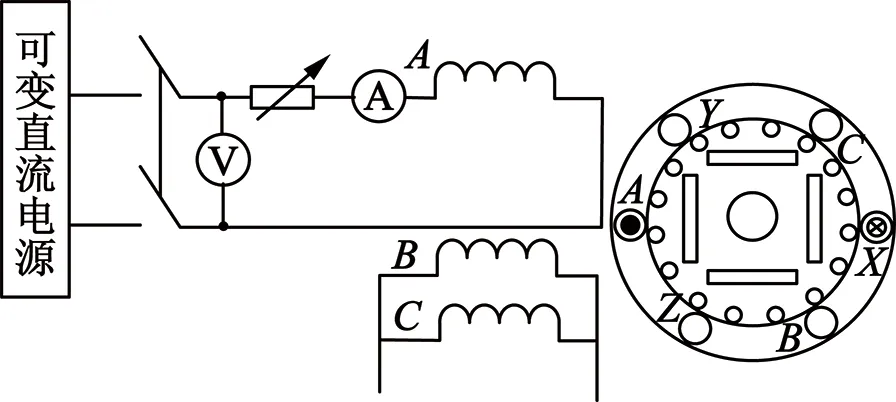
图10 永磁同步电动机转子位置检测实验线路

图11 实验装置图

3.1 转子极性判断实验

实验首先利用可调压直流电源向电机A相绕组中通入直流电的方法实现转子d，q轴的定位。

实验时将转子N极固定于AX绕组轴线方向上，将BC-YZ绕组并联，并在BC-YZ绕组间施加直流偏置电压。选择频率为2 Hz的低频电压信号注入电机AX绕组，并检测AX绕组中电压和电流的值，从而计算得到低频阻抗的值。

改变BC绕组间直流偏置电压的大小与方向，根据上述计算得出的低频阻抗特性如图12所示。

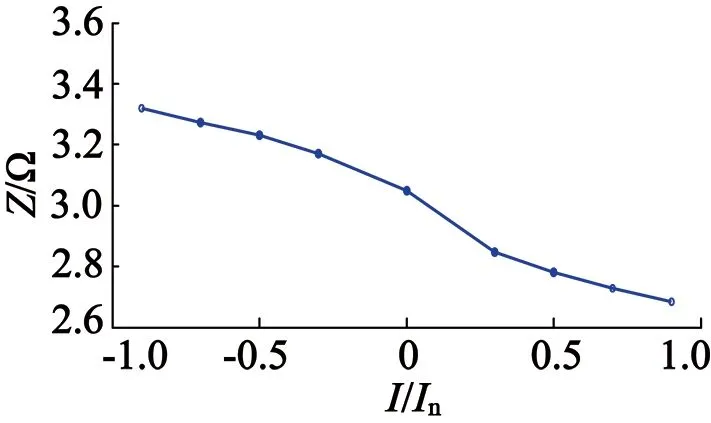
图12 叠加直流信号下的低频阻抗特性

可以发现，当BC-YZ绕组中叠加正向电压时，直流信号起助磁作用，磁路饱和程度增加，磁阻变大，低频阻抗的值变小；叠加反向电压，低频阻抗变大。实验结果符合理论分析。

3.2 高频注入转子位置检测

选用400 Hz高频电压信号注入电机AX绕组，实验过程中改变转子位置角，检测AX绕组中的电压与电流，计算得到高频漏阻抗与转子机械角度的关系如图13所示。

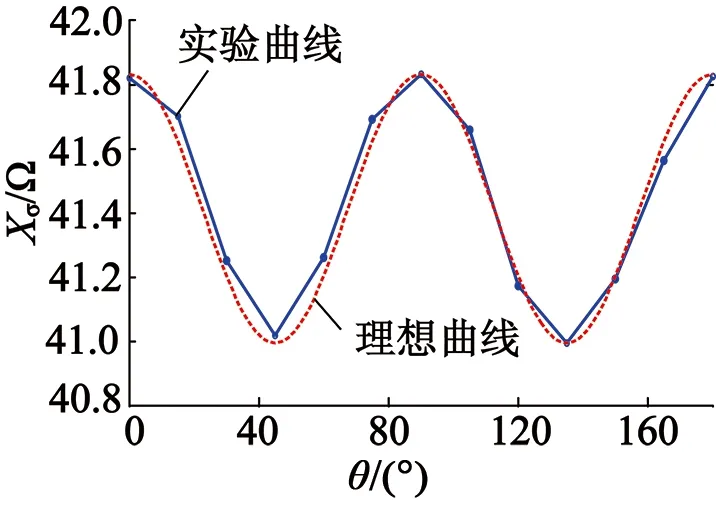
图13 漏阻抗与转子位置的关系

实验采用2对极电机，其机械周期与电周期成2倍关系。由实验曲线可知，当转子的机械角度为0°，高频漏阻抗最大；机械角度为45°，高频漏阻抗最小。实验结果符合理论分析。

根据测得的交直轴漏阻抗，代入式(3)绘制出高频漏阻抗与转子位置关系的理想曲线，按照该理想曲线可以得到基于高频信号注入的电机转子位置角度的估计。

3.3 低频注入转子位置检测

选用频率为2 Hz低频电压信号注入电机AX绕组，改变电机转子位置角，检测绕组中电压和电流的大小，由此计算得到不同转子机械角度下低频阻抗的值，如图14所示。

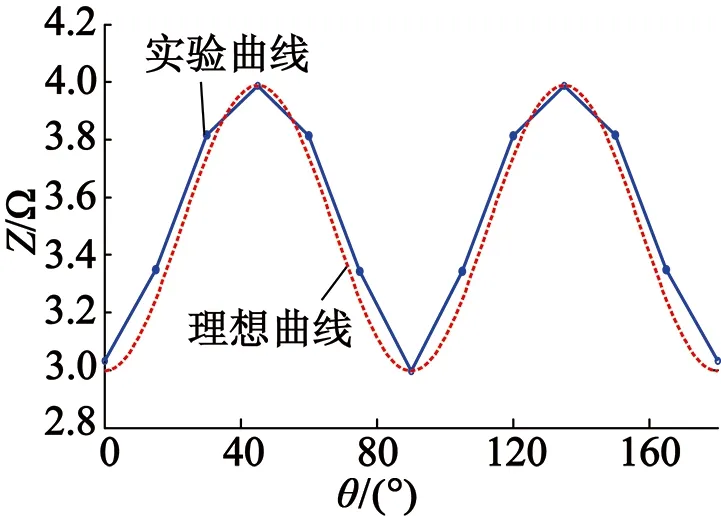
图14 低频阻抗与转子位置的关系

可以发现，当转子机械角度为0°，此时对应电机d轴位置，低频阻抗最小；当机械角度为45°时，低频阻抗达到最大值，与理论分析相吻合。

根据测得的交直轴低频阻抗，代入式(4)绘制出低频阻抗与转子位置关系的理想曲线，从而可以得到基于低频信号注入的电机转子位置角度的估计。

3.4 误差分析

为验证信号注入法估算转子位置角度在实际应用中的精度，将实验曲线中各个位置角度下的阻抗值代入绘制的理想曲线中，经公式反推出理想位置角度，两者角度相减后得出误差角度的绝对值，如图15所示为计算后的误差曲线。

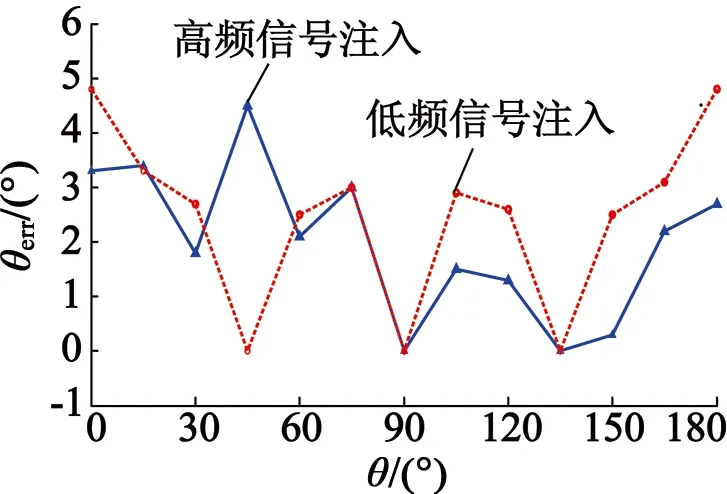
图15 误差曲线

由误差曲线可得，采用信号注入法估算转子位置时，其结果存在一定误差。其中，低频信号注入法估算转子位置的误差在0°～4.8°范围内；高频信号注入法的估算误差在0°～4.5°范围内。该误差范围较小，因此实验结果证明，利用信号注入法可以有效的实现永磁同步电动机转子位置的检测。

4 结 论

本文给出了具有阻尼绕组永磁同步电动机定子端注入单相信号时的等效电路，并对基于单相信号注入法辨识转子位置的原理进行了研究分析。即采用高频信号注入检测电机的高频漏阻抗；采用低频信号注入检测电机的低频阻抗，从而根据阻抗特性估算转子位置角度，并在低频信号注入的同时添加直流偏置信号鉴别转子磁极的极性。利用有限元方法对具有阻尼绕组永磁同步电动机进行了仿真分析，有效地提取出了转子位置信息。仿真和样机实验结果均表明基于单相信号注入的方法能够有效辨识出转子位置，鉴别转子永磁体的极性，对于永磁同步电动机的无传感器控制技术有良好的应用效果。

[1] 唐任远.现代永磁电机理论与设计[M].北京:机械工业出版社,2012.

[2] 刘颖.永磁同步电机脉振高频信号注入无位置传感器技术研究[D].南京：南京航空航天大学,2012.

[3] 陈书锦,李华德,李擎,等.永磁同步电动机起动过程控制[J].电工技术学报, 2008,23(7):39-44.

[4] 贾洪平,贺益康.基于高频注入法的永磁同步电动机转子初始位置检测研究[J].中国电机工程学报,2007,27(15):15-20.

[5] 苏健勇,杨贵杰,李铁才.PMSM 扩展状态滑模观测器及转子位置和速度估算[J].电机与控制学报,2008,12(5)：524-533.

[6] 王子辉,叶云岳.反电势算法的永磁同步电机无位置传感器自启动过程[J].电机与控制学报,2011,15(10):36-42.

[7] 王高林,杨荣峰,李刚,等.基于高频信号注入的IPMSM无位置传感器控制策略[J].电工技术学报,2013,27(11):62-68.

[8] 刘海东,周波,郭鸿浩,等.脉振高频电压注入法误差分析[J].电工技术学报,2015,30(6):38-44.

[9] 刘颖,周波,冯瑛,等.永磁同步电机低速无传感器控制及位置估计误差补偿[J].电工技术学报,2012,27(11):38-45.

[10] 李毅拓,陆海峰,瞿文龙,等.一种新颖的永磁同步电机转子初始位置检测方法[J].中国电机工程学报,2013,33(3):75-82.

[11] 徐艳平,郜亚秋,钟彦儒.基于低频信号注入法的PMSM低速无传感器控制[J].电力电子技术,2011,45(3):62-63.

[12] 徐艳平,郜亚秋,钟彦儒.低频信号注入法的永磁同步电机无速度传感器控制[J].电气传动自动化,2010,32(1):13-16.

[13] THIEMANN P，MANTALA C，HORDLER J,et al.PMSM sensorless rotor position detection for all speeds by direct flux control[C]//2011 IEEE International Symposium on Industrial Electronics.IEEE,2011:673-678.

[14] BASIC D,MALRAIT F,ROUCHON P.Initial rotor position detection in PMSM based on low frequency harmonic current injection[C]//14th International Power Electronics and Motion Control Conference.IEEE,2010:139-141.

[15] 郭志荣,谢顺依,高巍.带阻尼绕组的凸极永磁同步电机转子位置估计[J].中国电机工程学报,2009,29(36):55-59.

[16] 邓先明,汪文文,庞晴晴.永磁同步电机无传感器位置检测[J].实验室研究与探索,2015,34(4):112-116.

Rotor Position Identification of Permanent Magnet Synchronous Motor with Damper Windings

DENGXian-ming,LIShao-wu,LIUNa

(China University of Mining and Technology,Xuzhou 221116,China)

In order to overcome the problem of difficult installation and low reliability of the position sensor in control system, the sensorless rotor position identification of permanent magnet synchronous motor (PMSM) based on single-phase signal injection was proposed. The principle of single-phase signal injection method applied to the rotor position identification of PMSM with damper windings was analyzed. The impedance characteristics of the motor were detected to calculate the rotor position accurately by injecting a single-phase high frequency or low frequency signal, and the DC bias method was used to identify the polarity of the permanent magnet at the same time. The relationship between the impedance characteristics and rotor position of PMSM with damper windings was simulated and analyzed based on the finite-element method. The simulation and the prototype experiment show that the rotor position identification based on single-phase signal injection is feasible, which provides a good theoretical basis for the practical application of sensor-less control technique of PMSM.

permanent magnet synchronous motor (PMSM); damper winding; signal injection; rotor position identification; finite element analysis

2016-03-16

TM341；TM351

A

1004-7018(2016)12-0006-05