PMSM伺服系统的自适应模糊滑模切换控制

史晓娟，杨紫艳

(西安科技大学，西安 710054)

PMSM伺服系统的自适应模糊滑模切换控制

史晓娟，杨紫艳

(西安科技大学，西安 710054)

为了提高系统扰动较大时永磁同步电动机伺服系统位置跟踪响应的快速性和精确性，在普通滑模控制策略中引入自适应模糊控制算法，设计了基于自适应律的模糊滑模切换控制器。通过Lyapunov稳定性分析设计参数自适应律，同时也证明了控制系统的稳定性。通过理论分析、MATLAB/Simulink纯仿真实验以及基于AD5435的半实物仿真实验，验证了该算法在系统扰动较大时不仅能保证系统鲁棒性，而且能有效抑制系统抖振，使永磁同步电动机伺服系统获得准确的位置响应。

永磁同步电动机；模糊滑模控制；自适应律；位置伺服系统

0 引 言

永磁同步电动机(以下简称PMSM)由于控制结构简单、转动惯量低、体积小、输出转矩大、功率密度高、运行可靠且易于维护等优点，广泛应用于高性能位置伺服系统[1]。但是，PMSM又是一个多变量、强耦合的非线性系统，为了提高其控制精度并保证系统鲁棒性，算法鲁棒性好的滑模控制被广泛应用于PMSM位置伺服系统[2-3]。但是，普通滑模控制中存在开关切换动作的时间滞后、空间“死区”、状态变量测量误差以及时间离散等不利因素，控制系统常常会出现抖振问题。滑模控制的抖振问题本质上是由于其控制律中存在不连续的切换项引起的。而且，系统干扰较大时，控制律中的切换增益也会随之增大以保证滑模系统的稳定性，从而加剧系统抖振[4-8]。

到目前为止，人们已经为削弱滑模控制系统的抖振做了很多努力，如文献[9]张晓光等人提出了一种新型趋近率，该方法不仅降低了滑模控制的抖振问题，而且有效提升了滑模趋近速率；文献[10-11] Castanos F.等人提出了一种积分型滑模变结构控制器，仿真实验表明基于该控制器的系统具有响应快、无超调、鲁棒性好等优点；文献[12]中朱俊杰等人提出采用分段式滑模变结构状态重构法抑制抖振；文献[13]刘红俐等人在滑模变结构中引入了模糊控制，有效地抑制了普滑模变结构控制中的固有抖振问题；文献[14]中吴志飞等提出了一种基于自适应算法的滑模观测器，实验结果表明驱动系统具有优良的动、静态控制性能；文献[15]中姜红等人在模糊滑模控制的基础上，提出了一种自适应模糊滑模控制算法，实验结果证明该方法不仅能提高控制系统的响应性能，而且对参数变化具有鲁棒性。虽然以上方法在一定程度上能抑制抖振，但是当系统扰动较大时，其对系统抖振的抑制效果甚微。从本质上讲，滑模控制的抖振问题是由于控制律中存在不连续的切换项所导致的。而且，系统干扰较大时，控制律中的切换增益也会随之增大以保证滑模系统的稳定性，从而加剧系统抖振。针对这种情况，本文利用自适应模糊控制算法，通过模糊逼近滑模控制器中控制律的切换项，以达到将切换项连续化的目的，从而实现即使系统扰动较大，该算法也能简单、有效地减弱系统抖振。

1 PMSM位置伺服系统的数学模型

本文采用基于d-q轴同步旋转坐标系下的PMSM数学模型，对于表面式永磁同步电动机有Ld=Lq，其数学模型如下：

(1)

式中：ud，uq为d，q轴定子电压；id，iq为d，q轴定子电流；Rs为定子电阻；Ld，Lq为定子电感；Tl为负载转矩；J为转动惯量；B为粘滞摩擦系数；p为极对数；ω为转子角速度；ψf为永磁磁通。

式(1)表明永磁同步电动机是一个非线性多变量的控制系统。其伺服系统一般采用三环控制结构，从内到外依次是电流环、速度环以及位置环。PMSM位置伺服系统的结构如图1所示。

图1 PMSM位置伺服系统

本文速度调节器和电流调节器均采用PI控制，位置调节器采用自适应模糊滑模切换控制策略。

设位置环实际值为θ，设定值为θd，那么：

(2)

式中：ωr是电机转子角速度ωr=ω/p。

采用id=0的矢量控制，由式(1)和式(2)得：

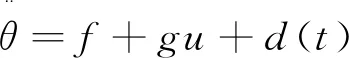
(3)

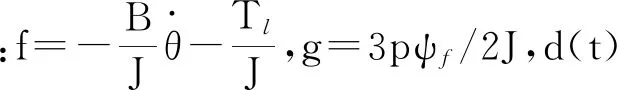
2 自适应模糊滑模切换控制器设计

2.1 滑模控制器设计

定义切换函数：

(4)

式中：e=θ-θd，c1>0满足Hurwitz多项式条件。

设计滑模控制律如下：

(5)

式中：usw=ηsgn(s)，切换增益η>D。

由式(3)和式(4)，可得：

(6)

将式(5)代入式(6)，得：

(7)

则:

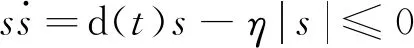
(8)

系统满足广义滑模条件，并且在滑动模态下是渐进稳定的。

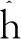
2.2 自适应模糊滑模切换控制器的设计

本文所设计的PMSM位置伺服系统结构框图如图2所示。

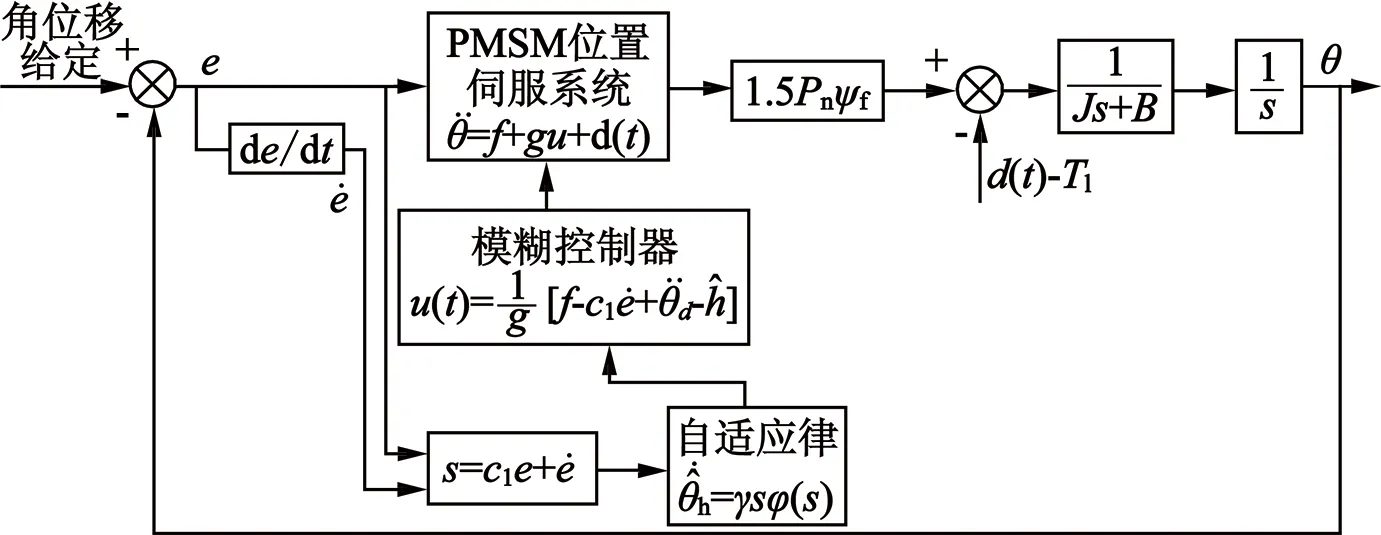
图2 PMSM位置伺服系统结构框图

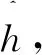
(9)

(10)

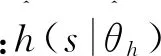
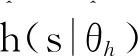
(11)

设计自适应律:

(12)

式中：γ为自适应参数。

由式(7)和式(10)，可得：

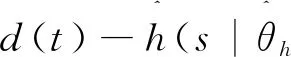
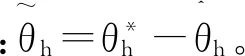
取Lyapunov函数形式如下：

(13)

则：

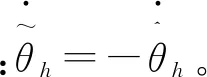
将自适应律式(12)代入上式，可得：

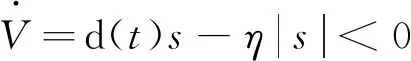
(14)

由此可以证明，图2中所设计的自适应模糊滑模切换控制器是稳定的。

3 系统仿真分析

3.1 抑制抖振有效性分析

首先，为验证自适应模糊滑模切换控制算法能有效地抑制抖振，将PMSM伺服系统的位置环分别采用普通滑模控制和自适应模糊滑模切换控制，系统扰动均设为d(t)=10sint，对比分析这两种控制策略的仿真结果，以验证自适应模糊滑模切换控制策略的有效性和优越性。

位置环采用普通滑模控制策略时，仿真系统的位置、速度跟踪曲线和控制输入曲线如图3所示。

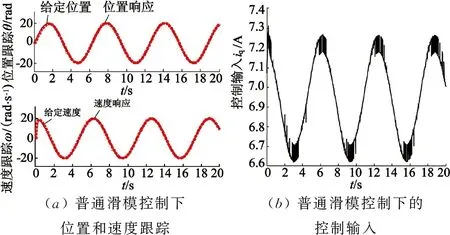
图3 基于SMC控制策略的系统仿真结果

由图3(a)可以看出，系统在仿真初始时刻1s左右，其位置跟踪滞后，速度响应产生了超调和振荡；图3(b)中普通滑模控制器输出的交轴电流iq抖振现象明显。

位置环采用自适应模糊滑模切换控制策略时，根据图2建立的MATLAB/Simulink仿真模型如图4所示。

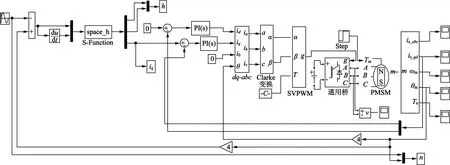
图4 基于自适应模糊滑模切换控制策略的PMSM位置伺服系统仿真模型

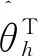
定义切换函数s(t)的隶属函数：

(15)

μZ(s)=exp (-s2)

(16)

(17)

采用控制律式(9)和自适应律式(12)，得到系统仿真结果如图5所示。对比图3(a)和图5(a)，当位置给定为θd(t)=20sint，干扰为d(t)=10sint，可以看出自适应模糊滑模切换控制策略的位置和速度响应上升时间很短，系统可快速到达给定位置，几乎没有振荡和超调；对比图3(b)和图5(b)可以看出，系统控制输入几乎没有抖振；图5(c)可以看出该策略能有效地将控制律中的切换项连续化。综上所述，在普通滑模控制中引入切换自适应模糊算法可以有效拟制滑模系统抖振，提高永磁同步电动机伺服系统位置跟踪响应的快速性和准确性。

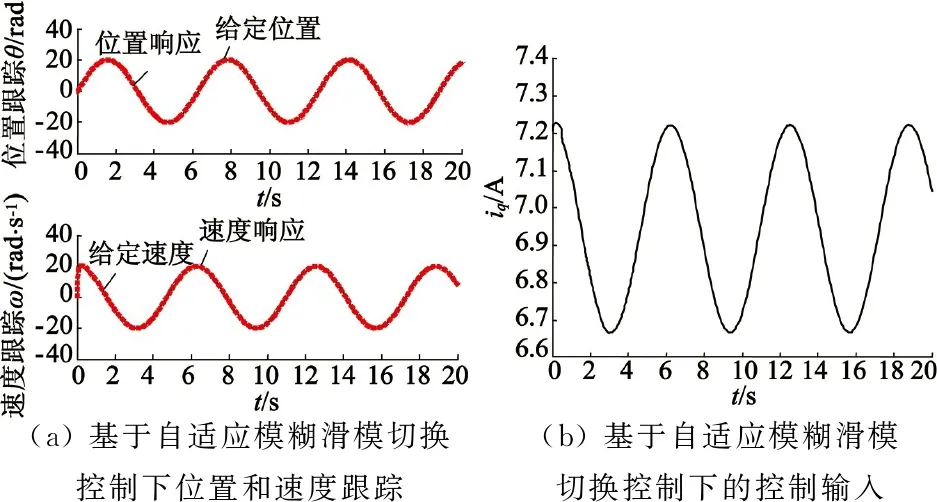
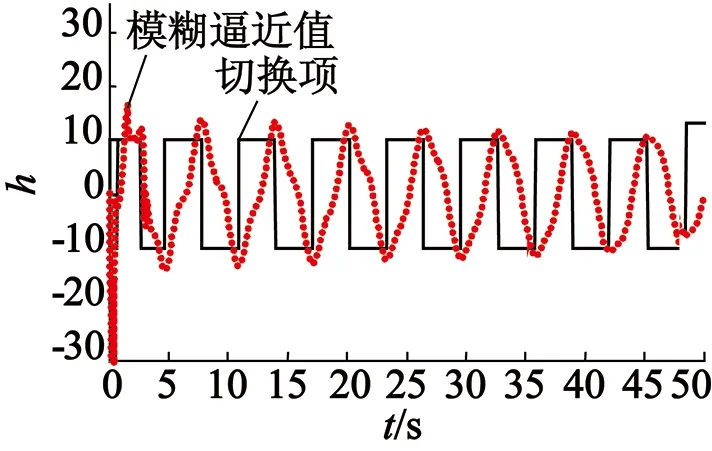
(c) 切换项及其模糊逼近值

3.2 系统抗扰动实验分析

当系统扰动较大时，为了验证自适应模糊滑模切换控制策略仍能有效地抑制系统抖振。本文在原有模型的基础上，成比例依次增大系统扰动d(t)，使得d(t)=20sint，d(t)=40sint，PMSM位置伺服系统固有参数不变，只需根据系统扰动分别调节自适应律中的参数为γ=17，γ=26。将两组参数代入图4的仿真模型中调试，得到结果如图6、图7所示。

由仿真结果可以看出，即使系统扰动不断增大至给定信号的2倍，引入的自适应模糊滑模切换控制算法仍能有效地拟制系统抖振，且其位置响应和

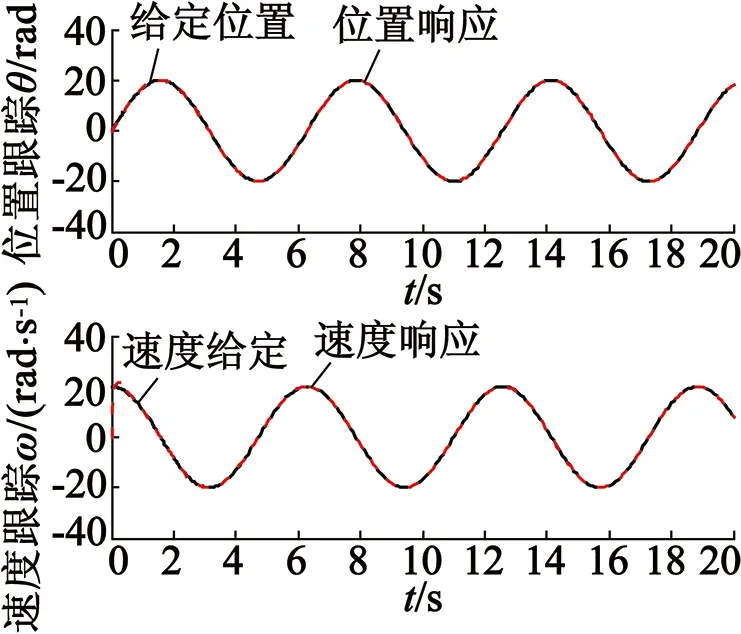
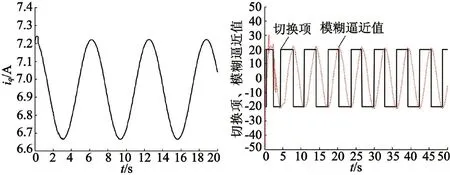
图6d(t)=20sint，γ=17时的仿真模型

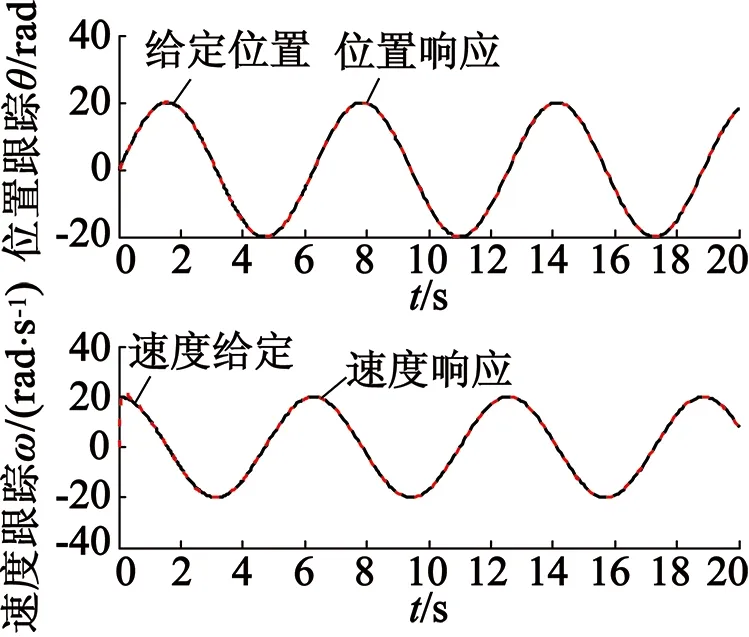
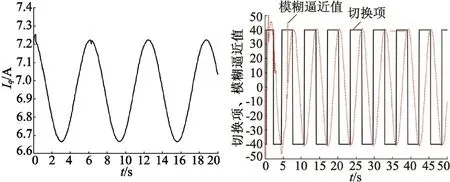
图7d(t)=40sint，γ=26时的仿真模型

速度响应性能也没有因此减弱，仍能快速跟踪给定的位置信号。实验表明该算法在减弱系统抖振的同时能保证永磁同步电动机伺服系统位置跟踪响应的快速性和准确性。

4 基于AD5435半实物仿真系统的实验研究

为了验证自适应模糊滑模切换控制算法的优越性和有效性。在MATLAB/Simulink仿真模型的基础上进行半实物实验验证，以充分证明本文中所提出的自适应模糊滑模切换控制算法的完善性。根据控制原理所搭建的基于AD5435的实验平台主要由上位机、控制器、驱动装置、执行电机以及显示输出等五大模块组成；系统软件控制程序是由已建立的MATLAB/Simulink程序所改写。

建立永磁同步电动机位置伺服系统的半实物仿真实验平台如下所示，其中，图8为位置伺服系统的半实物仿真结构图；图9为实验平台的硬件图。

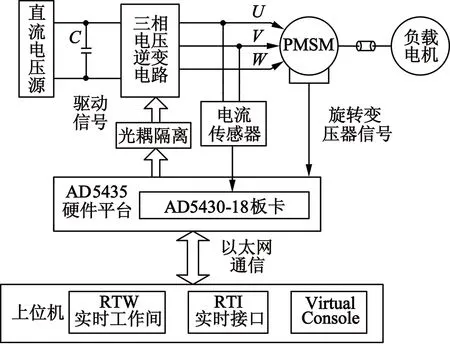
图8 永磁同步电动机位置伺服系统的半实物仿真结构图

图9 实验平台的硬件实物图

该实验平台的搭建主要包含以下6个模块：载有MATLAB以及AD5435相关控制软件的上位机模块，主要用于位置伺服系统建模和实验数据监测；核心控制模块AD5435 仿真机，它与上位机的通讯方式为以太网；永磁同步电动机的功率驱动模块采用的是Microchip公司的PICDEMTMMCLV开发板，主要包括驱动电路和电源电路等；AD5430-18板卡，主要用于输出三相PWM波，AD采样输入以及旋转变压器信号输入；电流传感器HS04-6A-NP，主要用于检测控制电机的电流信号；旋转变压器，采用的是双赢公司研发的YS 36XFW975，其作用是测量被控电机的转轴角位移。

4.1 正弦响应实验

本文再次对基于两种控制策略的位置伺服系统进行了正弦响应实验，系统给定位置指令为θd(t)=20sint，电机负载Tl=5 N·m，系统扰动为d(t)=10sint。系统的位置和速度响应曲线如下所示，其中，图10分别为普通滑模控制和自适应模糊滑模切换控制下系统的位置、速度响应对比图，根据图10(a)和10(b)可以看出采用普通滑模控制时，因为存在系统抖振，位置和速度响应曲线存在振荡和超调，系统跟随性能一般；而采用自适应模糊滑模切换控制时，系统抖振已经减弱，它的位置和速度跟踪性能明显优于普通滑模控制。实验结果充分证明了本文所提出的基于自适应模糊滑模切换控制策略的系统响应性能更好，且系统抖振也明显降低。

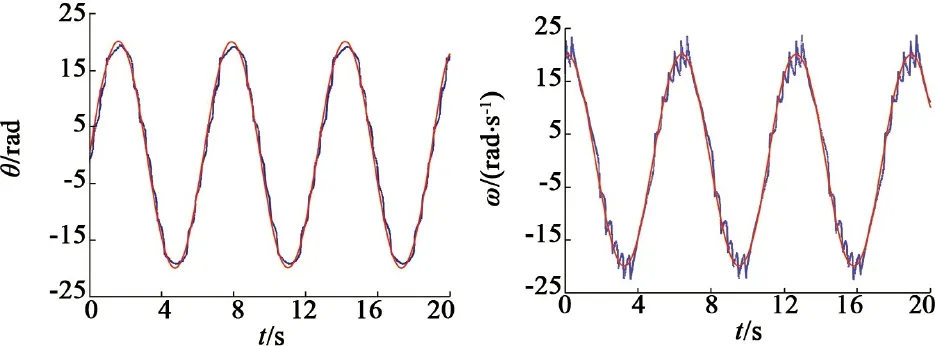
(a)普通滑模控制的位置和速度响应

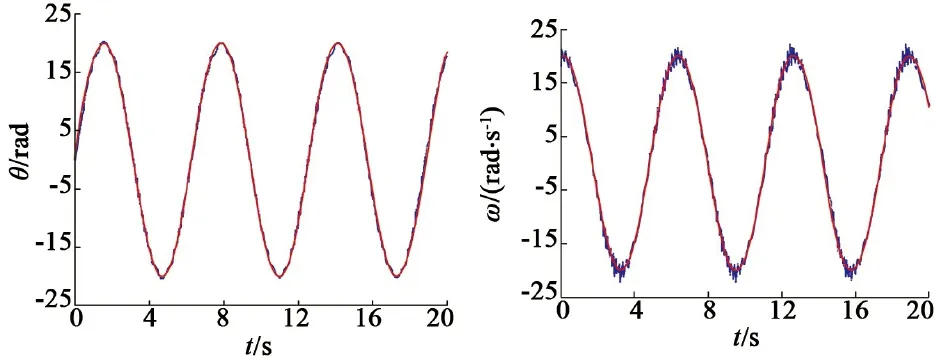
(b)自适应模糊滑模切换控制的位置和速度响应

图10 两种位置控制策略的位置正弦响应曲线

4.2 系统扰动变化实验

上文已采用纯仿真的方法验证了理论分析的正确性，仿真结果证明了即使系统外部干扰增大至给定信号的数倍，基于自适应模糊滑模切换控制策略的系统性能仍能保持良好。为了再次验证该策略的抗干扰性，进行了系统扰动变化实验，通过成比例依次增大系统扰动d(t)，使得d(t)=20sint，d(t)=40sint。实验结果如图11所示，将这两组响应曲线与图10对比发现基于自适应模糊滑模切换控制策略的系统位置、速度响应性能依然优越。

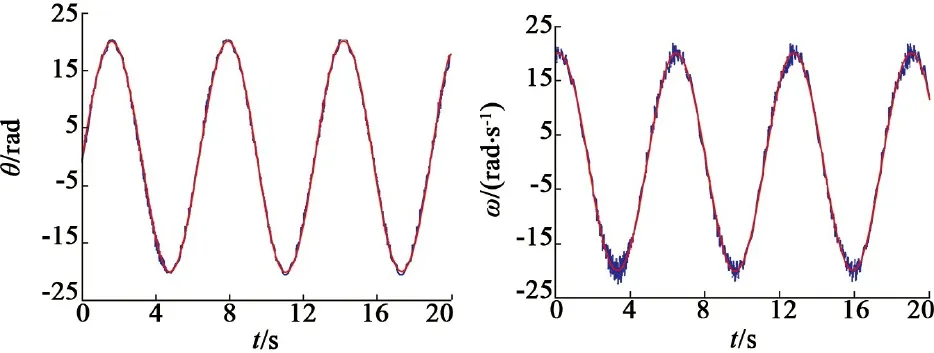
(a)干扰d(t)=20sint的位置和速度响应

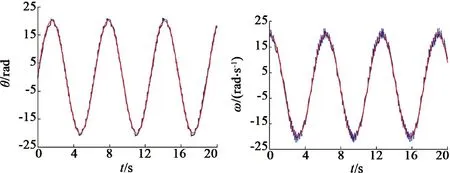
(b)干扰d(t)=40sint的位置和速度响应

图11 不同干扰下系统的位置和速度响应

5 结 语

本文在普通滑模控制的基础上，对于PMSM位置伺服系统，提出了基于自适应律的模糊滑模控制算法，有效地抑制了系统扰动较大时的抖振问题。在MATLAB/Simulink中建立了相应的仿真模型，并与普通滑模控制系统对比分析，结果表明该策略不仅可以有效拟制系统抖振，还能提高系统的位置响应性能。不断增大原有模型的系统扰动，验证了该策略在扰动较大时既能保证系统鲁棒性，又能有效地抑制系统抖振。最后，搭建基于AD5435的半实物仿真实验平台进一步验证了自适应模糊滑模切换控制策略能有效提高系统扰动较大时永磁同步电动机伺服系统位置响应的快速性和精确性。

[1] 陈荣.永磁同步电机控制系统[M].北京：中国水利水电出版社，2009.

[2] ZEROUG H,HOCINE L.Sensorless control of a surface mounted permanent magnet motor by signal injection associated with space vector modulation technique[C]//IEEE International Electronics Machines and Drives Conference.2009:153-184.

[3] 王丰尧.滑模变结构控制[M].北京：机械工业出版社，1995.

[4] LAI K C,SHYU K K．A novel motor drive design for incremental motion system via slidingmode control method[J]．IEEE Transaction on Industrial Electronics，2005，52(2)：499—507.

[5] 诸静.模糊控制原理与应用[M].北京：机械工业出版社，2005.

[6] 刘金琨.滑模变结构控制MATLAB仿真[M].北京：清华大学出版社，2012.

[7] 韩俊峰.永磁同步电机伺服系统的自适应模糊滑模控制研究[D].哈尔滨:哈尔滨工业大学,2014.

[8] 黄石维，周国荣.永磁同步电机的模糊滑模控制[J].机械工程及自动化，2010(2)：151-153.

[9] 张晓光，赵克，孙力,等.永磁同步电动机滑模变结构调速系统新型趋近率控制[J].中国电机工程学报，2011,31(24)：77-82.

[10] CASTANOS F,FRIDMAN L.Analysis and design of intergral sliding manifolds for systems with unmatched perturbations[J].IEEE Transaction on Automatic Control,2006,51(5):853-858.

[11] 李政,胡广大,崔家瑞,等.永磁同步电机调速系统的积分型滑模变结构控制[J].中国电机工程学报,2014,34(3):431-435.

[12] 朱俊杰，粟梅，王湘中,等.分段式滑模变结构无刷直流电机直接转矩控制[J].仪器仪表学报,2013,34(11):2634-2640.

[13] 刘红俐，张鹏，朱其新,等.基于新型趋近律的积分模糊滑模控制及其在PMSM控制中的应用[J].航天控制，2014,32(6):81-86.

[14] 吴志飞，张兴华，孙振兴.基于自适应滑模观测器的感应电动机直接转矩控制[J].微特电机，2013,41(10):64-67.

[15] 姜红,韩俊峰.PMSM伺服系统的自适应模糊滑模控制[J].微电机,2014,47(5):46-49.

Fuzzy Adaptive Sliding Mode Switching Control For PMSM Servo System

SHIXiao-juan,YANGZi-yan

(Xi’an University of Science and Technology University, Xi’an 710054)

In order to improve the speed and accuracy of the position tracking response of permanent magnet synchronous motor servo system when the system was disturbed, a fuzzy sliding mode controller based on adaptive law was designed by combining switching fuzzification adaptive control algorithm with traditional sliding mode control method. Through Lyapunov stability analysis, parameter adaptive laws was designed and the stability of servo system based on switching fuzzy adaptive sliding mode control algorithm was proved. When the system is disturbed, theoretical analysis, MATLAB/Simulink pure simulation experiment and the semiphysical simulation experiment based on AD5435 results show this algorithm can reduce chattering, has strong robustness and make PMSM servo system obtain accurate position response.

permanent magnet synchronous motor (PMSM)； fuzzy sliding mode control； adaptive law； position servo system

2016-06-22

国家自然科学基金项目(51275403)

周珍香(1981-)，女，讲师，研究方向为电气工程及其自动化。

TM341；TM351

A

1004-7018(2016)12-0058-05