一种改进的永磁同步电机最大转矩电流比控制方法

陈 吉，商红桃，王剑锋

(1.江苏联合职业技术学院 常州铁道分院，常州 213011；2.江苏联合职业技术学院 常州刘国钧分院，常州 213025；3.江苏省电力公司检修分公司 南通分部，南通 226000)

一种改进的永磁同步电机最大转矩电流比控制方法

陈 吉1，商红桃2，王剑锋3

(1.江苏联合职业技术学院 常州铁道分院，常州 213011；2.江苏联合职业技术学院 常州刘国钧分院，常州 213025；3.江苏省电力公司检修分公司 南通分部，南通 226000)

永磁同步电机的最大转矩电流比控制因可以降低电机的损耗而得到广泛应用。然而，传统的基于直接计算的永磁同步电机最大转矩电流比控制方法受电机参数变化的影响较大，而传统的基于扰动观察法的永磁同步电机最大转矩电流比控制方法无法兼顾动态特性和稳态性能。为了克服直接计算法和扰动观察法各自的缺点，提出了一种改进的基于扰动观察法的永磁同步电机最大转矩电流比控制方法。所提方法既提高了系统的稳态精度，又提高了系统的动态响应速度，从而可实现高性能的最大转矩电流比控制。仿真试验验证了所提方法的有效性。

永磁同步电机；最大转矩电流比控制；直接计算法；扰动观察法

0 引 言

永磁同步电机(Permanent Magnet Synchronous Motor， PMSM)因效率高等优点而广泛的应用于电动汽车驱动控制等工业场合[1]。与隐极式PMSM相比，凸极式PMSM通过利用磁阻转矩可进一步提高其驱动效率，因此得到更广泛应用。最大转矩电流比(Maximum Torque per Ampere，MTPA)控制就是一种可降低损耗的凸极式PMSM优化控制方法。顾名思义，MTPA控制就是指在输出转矩相同的情况下，保证电机的定子电流最小[2-6]。因此，MTPA控制可降低电机的铜耗。常用的MTPA控制方法主要包括直接计算法[7]、扰动观察法[8]和高频信号注入法[9]等。直接计算法根据PMSM的数学模型直接计算得到最优电流指令，在参数准确的前提下可以获得较高的控制精度。然而，PMSM的参数会随温度、磁场饱和程度的变化而变化，从而导致基于直接计算法的MTPA控制的控制精度急剧下降。为此，有学者研究了基于参数辨识的MTPA控制方法[10-11]，然而该方法并不能对电机的所有参数实现在线辨识。

为了克服直接计算法存在的缺点，有学者研究了基于扰动观察法的PMSM MTPA控制方法[8]。该方法通过在线扰动电流的角度，可以实时获得MTPA控制所对应的电流角度，从而可实现较高精度的MTPA控制。然而，该方法的扰动步长较难选择。扰动步长太小会导致系统的动态跟随特性较差，扰动步长太大又会导致系统的稳态性能较差。因此，该方法较难兼顾系统的稳态特性和动态特性。

此外，高频信号注入法也被应用于PMSM的MTPA控制[9]。然而，高频信号注入法的实现较复杂，需要合理设计滤波器对高频信号进行处理。其控制精度依赖于所设计的滤波器。此外，高频信号注入法也存在较大的稳态脉动。

为了克服传统MTPA控制所存在的缺点，本文提出了一种基于改进扰动观察法的PMSM MTPA控制方法。该方法将直接计算法和扰动观察法结合在一起，既可以提高MTPA控制对电机参数变化的鲁棒性，也可以通过选择较小的扰动步长来提高MTPA控制的稳态精度。因此，所提MTPA控制方法可以获得更好的动稳态特性。仿真试验验证了所提方法的有效性。

1 传统的基于直接计算的MTPA控制方法

在两相同步旋转d-q坐标系上，PMSM的电磁转矩可表示：

(1)

式中：id，iq分别为定子电流在同步旋转d，q轴上的两个分量；ψf为永磁体磁链；p为电机极对数；Ld为d轴电感；Lq为q轴电感。

假设电流矢量位于第二象限，如图1所示。

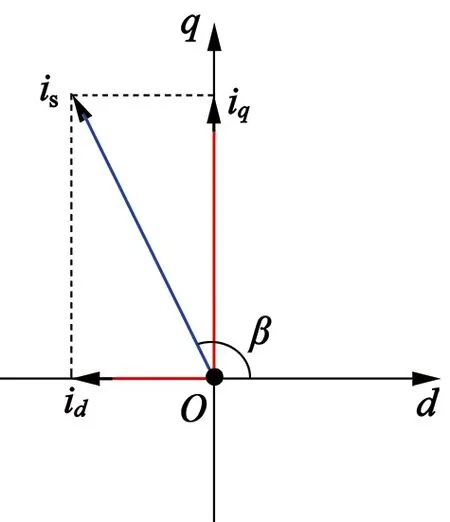
图1 电流矢量图

此时，由图1可得：

id=iscosβ

(2)

iq=issinβ

(3)

式中：is为电流矢量幅值;β为电流矢量的角度。

由式(1)～式(3)可得：

(4)

根据MTPA控制的定义，MTPA控制对应：

各县市区政府均成立了地质灾害防治领导小组，除城区各分局外，各县市区局均设有专门的地质灾害防治工作机构（地质环境股或地质环境储量股），耒阳、常宁和衡阳县还成立了地质环境监测站，其中，耒阳、常宁市局地质环境监测站为副科级二级事业单位。自2017年以来，根据省厅的统一要求，各县市区局还采取政府购买服务方式，分别与坐落在我市的4家地勘单位合作建立地质灾害防治技术指导中心，较好地解决了市县地质灾害防治缺技术、缺人员、缺装备等问题。此外，全市所有已查明的地质灾害隐患点均确定了一名监测员。

(5)

由式(4)～式(5)：

(6)

由式(2)～式(3)和式(6)可得：

(7)

(8)

式(7)～式(8)给出了实现MTPA控制的直接计算方法。由式(7)～式(8)可见，直接计算法完全依赖于PMSM的参数，因此其控制精度较差。

2 传统的基于扰动观察的MTPA控制方法

区别于直接计算法，扰动观察法通过对电流矢量的角度施加扰动，可在线获得MTPA控制所对应的电流矢量角度，从而可实现MTPA控制。以下分4种情况进行介绍。

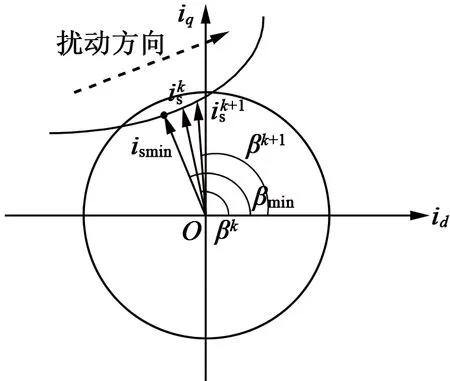
图2 扰动观察法情况1

图3 扰动观察法情况2

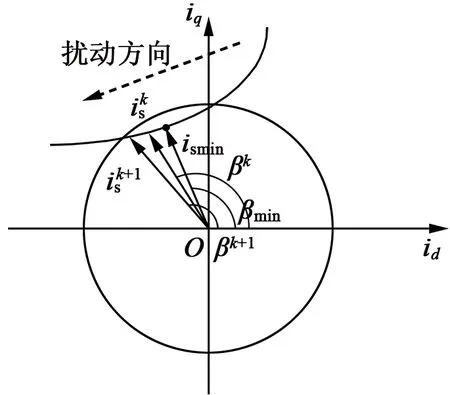
图4 扰动观察法情况3

由以上4种情况可得实现基于扰动观察法的PMSM的MTPA控制的算法流程图如图6所示。根据图6即可实现MTPA控制。

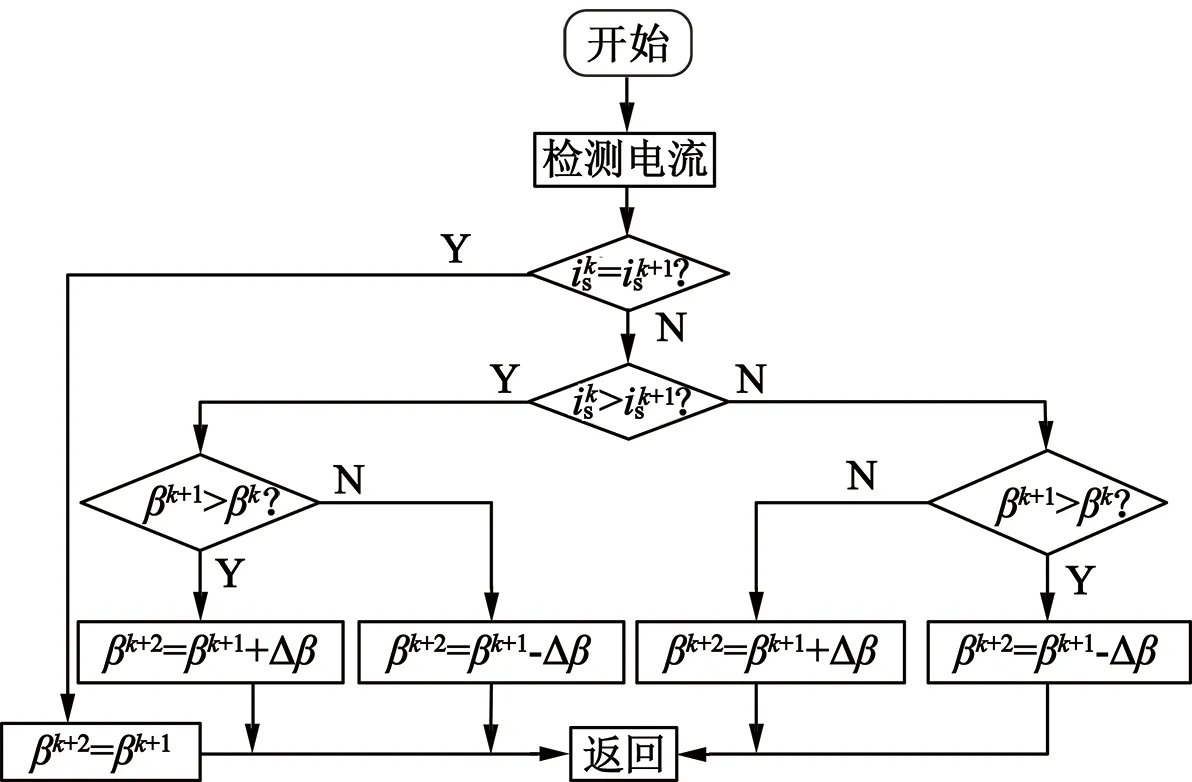
图6 基于扰动观察法的MTPA控制流程图

3 改进的基于扰动观察的MTPA控制方法

由前文可知，传统的基于直接计算的PMSM MTPA控制方法依赖于高精度的电机参数。而由于PMSM是一种高阶非线性强耦合系统，其参数会随运行条件发生变化，这导致直接计算法的控制精度较低。同时，采用扰动观察法实现MTPA控制虽然可以克服参数变化的影响，但其扰动步长较难选择。选择较大的扰动步长可以提高MTPA系统的动态收敛速度，但会导致其稳态转矩脉动较大。相反，选择较小的扰动步长虽然可以减小稳态转矩脉动，但其动态收敛速度会减慢。

为了克服传统的直接计算法和扰动观察法各自的缺点，并融合其各自的优点，本文提出了一种改进的基于扰动观测的PMSM MTPA控制方法。该方法根据电机的数学模型直接计算得到MTPA所需的电流矢量角度，然后在此基础之上对直接计算得到的电流矢量角度进行小扰动，以获得准确的电流矢量角度，从而既可以克服直接计算法存在的参数灵敏性问题，也可以解决扰动观察法存在的稳态转矩脉动较大的问题。所提方法的控制框图如图7所示。

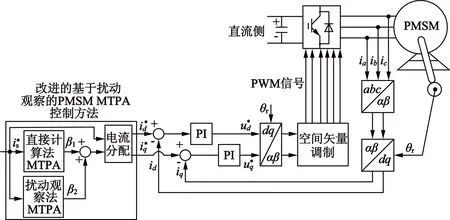
图7 改进的基于扰动观察法的PMSM MTPA控制方法

如图7所示，所提方法融合了直接计算法和扰动观察法各自的有点，并克服了各自的缺点，因此其动态响应速度和稳态控制精度都得到提高。

4 仿真试验

为了验证理论分析，基于MATLAB对所提方案进行了仿真试验研究。仿真中所使用的电机参数：Rs=0.03 Ω，Ld=0.013 H，Lq=0.025 H，ψf=1.16 Wb。

首先，本文对基于直接计算的MTPA控制方法进行了仿真验证，并于传统的id=0控制进行了对比。仿真时，采用转速闭环控制。转速指令设定为400 r/min，转速环输出为电流幅值，其限幅值设定为100 A。在0.3 s时负载由300 N·m突减为200 N·m，在0.6s时，负载由200N·m突减为100N·m。仿真结果如图8所示。由图8可见，在同样条件下，与id=0控制相比，采用MTPA控制的PMSM定子电流更小，因此MTPA控制有助于减小电机的铜耗。

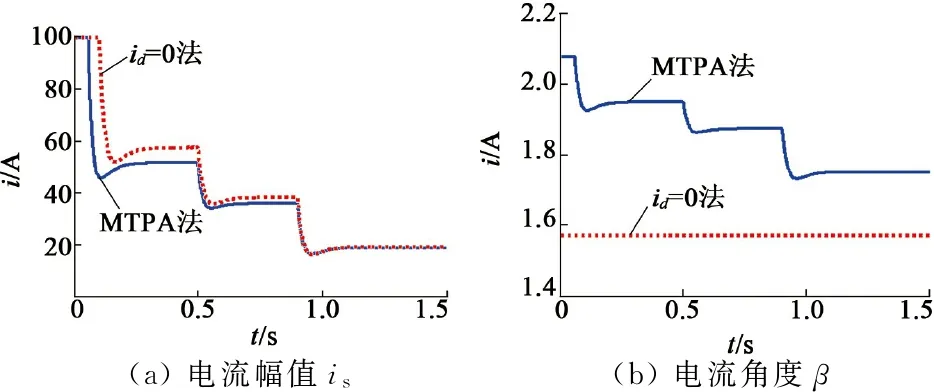
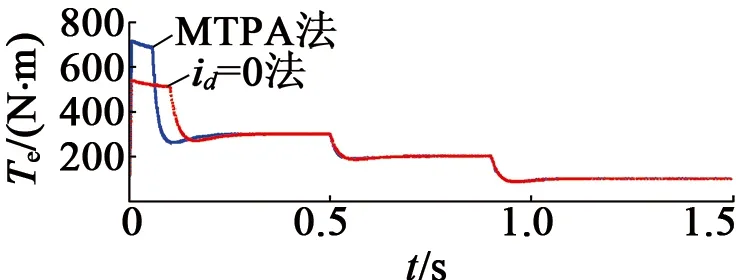
(c) 实际转矩Te

同时，需要指出的是，直接计算法对参数极为敏感，以下进行仿真验证。仿真时，电机运行在400r/min，负载转矩固定为300N·m，0.5s时参数发生变化。由于电机本体的参数较难改变，仿真中只改变控制器中使用的电机参数。图9给出了Ld变化时的仿真结果。由图9可见，当Ld出现偏差时，基于直接计算法的MTPA控制出现了角度偏差(如式(6)所示)，导致电流增大，即无法实现准确的MTPA控制。

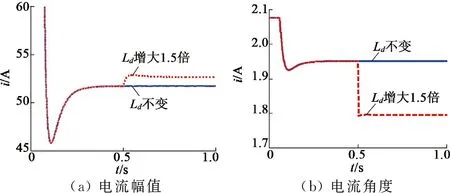
图9 Ld出现偏差时的仿真结果

同样条件下，图10给出了Lq变化时的仿真结果，图11给出了ψf变化时的仿真结果。由图10和图11可见，电机的参数变化均会影响直接计算MTPA控制方法的控制精度。

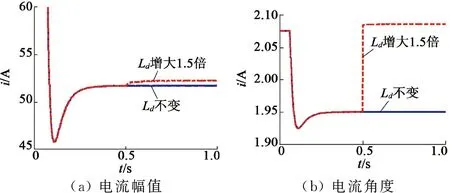
图10 Lq出现偏差时的仿真结果

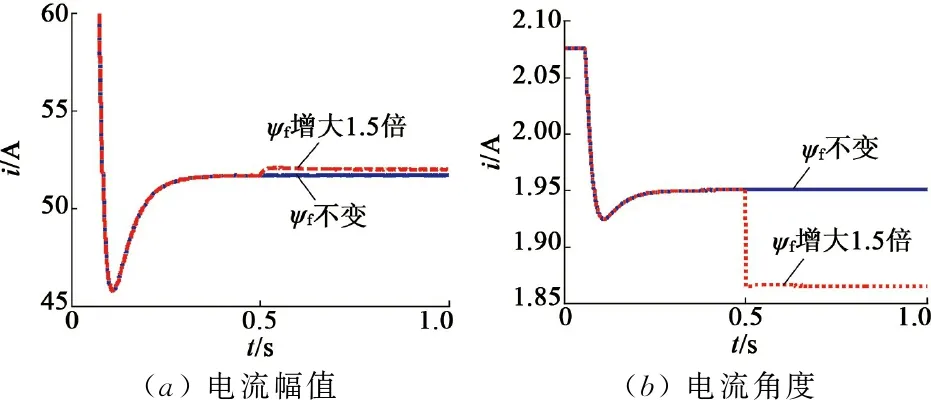
图11ψf出现偏差时的仿真结果

其次，对基于扰动观察法的MTPA控制进行仿真研究。在这个仿真中，采用转速闭环控制。转速指令设定为400 r/min，转速环输出为电流幅值，其限幅值设定为100 A，扰动步长设置为3°。在0.8 s时负载由300 N·m突减为200 N·m，在1.5 s时，负载由200 N·m突减为100 N·m。采用直接计算法和扰动观察法进行对比研究，仿真结果如图12所示。由图12可见，在稳态时，扰动观察法可以获得较高的MTPA控制精度，但在动态过程中，由于扰动步长较小，其收敛速度较慢。此外，由图12(d)可见，由于扰动观察法在稳态时也会不断进行扰动，导致其转矩脉动较大。步长越大，转矩脉动越大。

最后，重点对所提出的改进型MTPA控制方法进行了仿真验证，主要包括动稳态特性验证及参数鲁棒性验证。

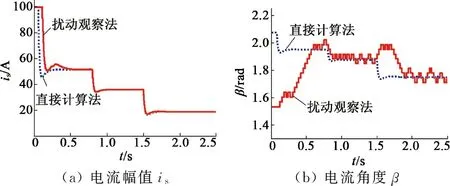
图12 基于扰动观察法的MTPA仿真结果

图13给出了改进的MTPA控制方法的动态仿真结果。在这个仿真中，通过MATLAB设置使PMSM运行于固定转速模式，并设定转速为400r/min，采用转矩闭环控制，电流矢量角度的扰动步长设为1°。在0.5s时转矩指令由200N·m突减为100N·m，在1s时转矩指令由100N·m突减为0，在1.5s时转矩指令由0突减为-100N·m，在2s时转矩指令突减为-200N·m，PMSM逐渐由电动状态过渡到发电状态。采用直接计算法和改进的扰动观察法进行对比研究。由图13可见，本文设计的改进型MTPA控制的动态收敛速度很快，这是因为该方法结合了直接计算法的优点。同时，该方法的稳态转矩脉动大大减小，这是因为该方法可以选择较小的扰动步长。

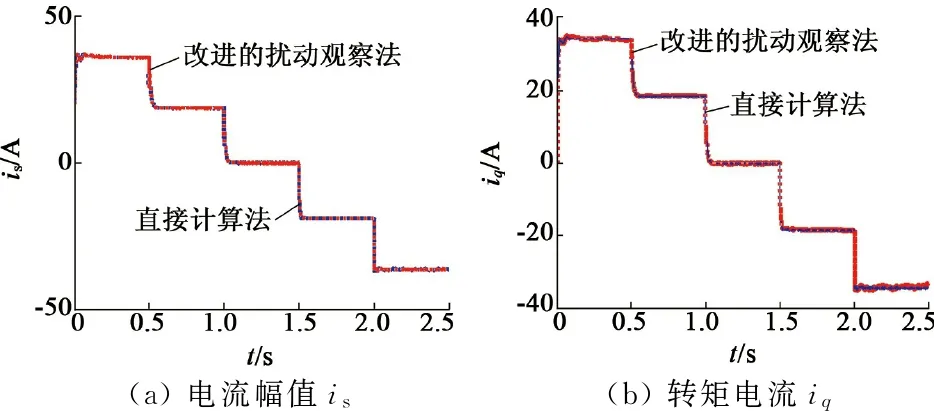
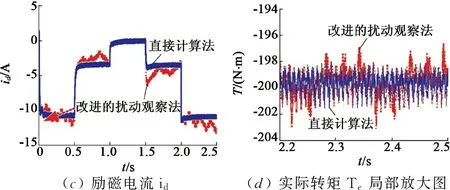
图13 基于改进的扰动观察MTPA控制的仿真结果

同时，图14～图16给出了改进型MTPA控制方法的参数鲁棒性仿真验证结果。由图14～图16可见，由于改进的扰动观察法结合了传统扰动观察法的优点，因此可以克服参数变化的影响，从而可提高MTPA控制的参数鲁棒性。

图14 Ld变化时改进的扰动观察MTPA控制方法的仿真结果

(a)电流幅值(b)电流角度

图15 Lq变化时改进的扰动观察MTPA控制方法的仿真结果

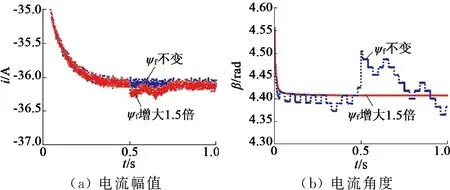
图16 ψf变化时改进的扰动观察MTPA控制方法的仿真结果

5 结 语

针对传统的PMSMMTPA控制所存在的问题，本文提出了一种基于改进型扰动观察法的PMSMMTPA控制方法。该方法融合了直接计算法的优点，因此其动态收敛速度和稳态控制精度都得到提高。同时，该方法融合了扰动观察法的优点，因此其对电机参数变化也具有较强的鲁棒性。仿真实验结果验证了所设计的改进型MTPA控制方法的有效性。

[1] 徐艳平,郭科，钟彦儒.基于强跟踪滤波器的PMSM无速度传感器DTC策略[J].系统仿真学报，2012，24(10):2197-2202.

[2] 赵志诚，桑海，张井岗.永磁同步电机速度伺服系统的分数阶内模控制[J].系统仿真学报，2015，27(2):384-388.

[3] 刘子建，吴敏，王春生，等.基于自适应观测器和自抗扰控制的PMSM直接转矩控制[J].系统仿真学报，2010，22(11):2702-2707.

[4] 张兴，郭磊磊，杨淑英，等．永磁同步发电机无速度传感器控制[J]．中国电机工程学报，2014，34(21)：3440-3447．

[5] 陈思溢，皮佑国.基于滑模观测器与滑模控制器的永磁同步电机无位置传感器控制[J]．电工技术学报，2016，31(12)：108-117．

[6] 左月飞，张捷，刘闯，等.基于自抗扰控制的永磁同步电机位置伺服系统一体化设计[J]．电工技术学报，2016，31(11)：51-58．

[7] 林立，黄苏融.基于精确线性化解耦的内置式永磁同步电机牵引系统[J].系统仿真学报，2009，21(20):6529-6533.

[8]NIAZIP,TOLIYATHA.Robustmaximumtorqueperamp(MTPA)controlofPM-assistedsynchronousreluctancemotor[C]//Twenty-FirstAnnualIEEEAppliedPowerElectronicsConferenceandExposition,APEC'06.IEEE,2006:685-692.

[9]BOLOGNANIS,PETRELLAR,PREAROA,etal.AutomatictrackingofMTPAtrajectoryinIPMmotordrivesbasedonACcurrentinjection[J]．IEEETransactionsonIndustryApplications，2011，47(1):105-114．

[10]KIMH,HARTWIGJ,LORENZRD.Usingon-lineparameterestimationtoimproveefficiencyofIPMmachinedrives[C]//IEEE33rdAnnualPowerElectronicsSpecialistsConference,PESC'02.IEEE,2002:815-820.

[11]MOHAMEDYA-RI,LEETK.Adaptiveself-tuningMTPAvectorcontrollerforIPMSMdrivesystem[J]．IEEETransactionsonEnergyConversion，2006，21(3):636-644．

An Improved Maximum Torque per Ampere Control Method for Permanent Magnet Synchronous Motor

CHENJi1，SHANGHong-tao2，WANGJian-feng3

(1.Changzhou Railway Institute of Jiangsu Joint Vocational and Technical College,Changzhou 213011,China;2.Changzhou Liu Guojun Institute of Jiangsu Joint Vocational and Technical College,Changzhou 213025,China;3.Jiangsu Electric Power Company Maintenance Branch Company Nantong branch,Nantong 226000,China)

The maximum torque per ampere (MTPA) control method of permanent magnet synchronous motor (PMSM) is widely used due to that it can reduce the loss of the motor. However, the conventional direct computing based MTPA control method of PMSM is heavily influenced by the motor parameters. The conventional perturbation and observation based MTPA control method of PMSM is unable to take into account the dynamic performance and steady-state performance at the same time. In order to overcome the drawbacks of the direct computing and perturbation and observation based MTPA control method, an improved perturbation and observation based MTPA control method for PMSM is proposed. The proposed method not only can improve the steady-state accuracy, but also can improve the dynamic response speed. As a result, high performance MTPA control is achieved. The simulation test verifies the effectiveness of the proposed method.

permanent magnet synchronous motor; maximum torque per ampere control; direct computing method; perturbation and observation method

2016-07-06

TM341;TM351

A

1004-7018(2016)12-0053-05

陈吉(1979-)，女，工程硕士，讲师，主要研究方向为电工电子技术理论与应用、智能控制等。