基于弱磁升速的永磁同步电机模型预测控制

余雨婷，滕青芳，柏建勇，韩思远

(1.兰州交通大学,兰州 730070;2.济南铁路局青岛电务段,青岛 266000)

基于弱磁升速的永磁同步电机模型预测控制

余雨婷1，滕青芳1，柏建勇2，韩思远1

(1.兰州交通大学,兰州 730070;2.济南铁路局青岛电务段,青岛 266000)

针对永磁同步电机在弱磁过程中容易产生转矩脉动的问题,在弱磁控制的基础上设计了有限集模型预测控制.有限集模型预测(Finite Control Set Model Predictive Torque Control, FCS-MPC)控制算法的实现需要利用整流器有限开关的状态特点,和电机的数学模型来预测系统的未来状态.同时，构造系统的目标函数，采用遍历法，在线进行寻优选出系统的最优开关状态.最后将目标函数选择的最优开关信号作为控制信号，以使系统稳定性更好.仿真和实验结果表明，所提出的控制策略使永磁同步电机的转矩脉动小、鲁棒性更好。

面贴式永磁同步电机；弱磁控制；恒磁链控制；有限集模型预测控制；稳定性

0 引 言

永磁同步电机(Permanent Magnet Synchronous Motor，PMSM)的结构比异步电机更加紧凑、且还具有功率密度大[1]、转子发热量小等优点，用永磁同步电机做主轴传动正在成为一个新的研究方向[2]。传动系统不仅要求低速时输出的转矩要大，还要求在加速的过程中，能在逆变器容量不变的情况下，调速的范围能较宽[3]。PMSM的弱磁控制策略能在维持逆变器容量不变的前提下而使系统的速度范围得以被拓宽[4]。基于弱磁控制的优点和意义,对于弱磁控制在升速过程中容易造成转矩和磁链的不稳定，学者们提出了许多用于改善弱磁控制性能的方法。文献[5]提出了单电流调节器控制算法，鲁棒性能好，但是在改变转速和转矩变化时最优直轴电压较难选择。文献[6]通过控制定子电流和直轴夹角控制定子电流，从而控制转矩,计算量大。文献[7]采用六步电压过调制法,能最大限度的利用直流母线电压，然而会产生很大的电流谐波，在整流阶段电流谐波的得不到抑制。文献[8-9]采用查表法实现永磁同步电机弱磁的优化控制，计算量大，实现起来较为复杂。

模型预测控制(Model Predictive Torque Control，MPC)开发于1970年代，并被应用于复杂的工业控制领域当中。MPC控制根据系统的所建立的动态模型和系统的当前状态来预测系统在未来的状态。建立的系统性能指标函数来计算系统在每个预测控制周期内的最优控制量，以使控制过程更加 快速并趋于平稳[10]。

基于MPC能提高系统稳定性的优点，本文在模型预测控制下对永磁同步电机磁链进行控制实现弱磁，设计了有限集模型预测模块。通过在弱磁控制过程中使用有限集模型预测来减小转矩的脉动，以使弱磁控制过程更趋平稳。

1 永磁同步电机弱磁控制原理

本文的电机模型建立在同步旋转d-q坐标系下，所采用的电机模型为面贴式永磁同步电机。

1.1 数学模型

电流方程：

(1)

磁链方程:

(2)

(3)

式中：ψd,ψq分别为d，q轴的磁链分量；Rs为定子电阻；Ld，Lq分别为d，q轴自感，且Ld=Lq=L；ψf为永磁体磁链；id，iq为d，q轴定子电流分量。

在模型预测转矩控制中，弱磁控制的实现是通过对电机定子磁链的调节来完成的，使弱磁控制系统运行于高速。在恒转矩区，当电机稳定运行时，忽略其定子电阻Rs压降，定子电压峰值可表示：

|us|=ωr|ψs|=

(4)

式中：us为电机定子端电压，ψs为定子磁链，ωr为机械角速度。

(5)

本文的弱磁控制基于模型预测控制系统，磁链幅值与电磁转矩的给定框图如图1所示。通过在模型预测控制系统下，控制定子磁链幅值达到弱磁控制的效果。当电机转速在转折速度ωrt以下时，电机的输出转矩通过含有限幅的速度PI调节器给定，给定一个恒定的定子磁链幅值，使电机工作于恒磁通控制方式；当转速在电机的转折速度ωrt以上时，系统运行于弱磁工作区，磁链幅值的变化与转速呈反比例关系，而转矩的变化也随转速的升高而逐渐减小。该方法下的非弱磁和弱磁状态之间的切换简单，计算量小，易于实现。

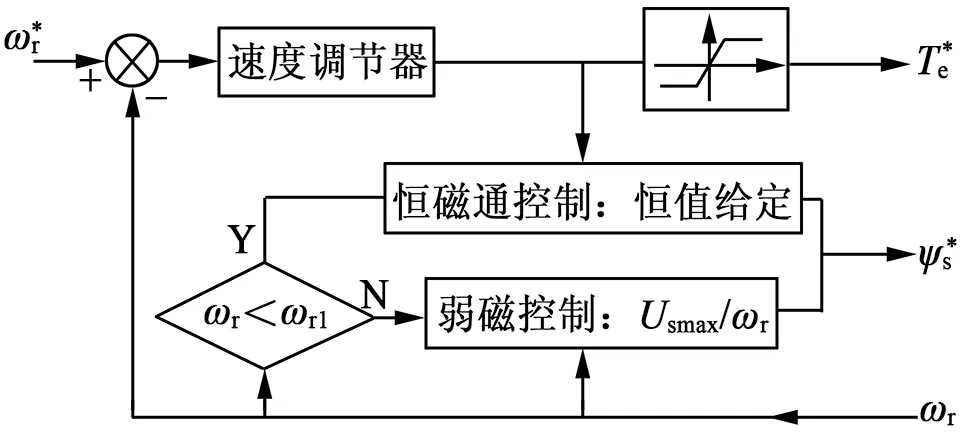
图1 弱磁控制器复合控制原理框图

2 有限集模型预测控制模块设计

有限集模型预测控制模块主要由电流预测模块、转矩磁链计算模块、成本函数最小化模块构成。

2.1 电流预测模块

对于面贴式电机直轴电感近似等于交轴电感即Ld=Lq=L,其数学模型由电流方程(1)进行欧拉离散化，得到电流方程的离散化模型：

(6)

式中：Ts表示采样间隔时间；k表示采样时刻；p为极对数。

2.2 转矩磁链计算模块

将转矩表达式欧拉离散化得到模型预测转矩：

(7)

同理，将磁链式(3)欧拉离散化得到模型预测磁链：

(8)

2.3 成本函数最小化模块

定义模型预测的成本函数如下：

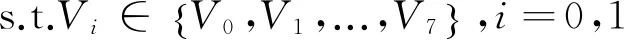
(9)

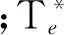
在成本函数中，由于同时含有电磁转矩和定子磁链，且2个量的量纲不同，B1的取值用来平衡2个量之间不同的量纲，使得转矩和磁链具有相同的权值。 的选取在目前还是一个未解决的难题[11]，在文献[12]中B1取值为Tn/ψn(Tn，ψn分别表示转矩和磁链的额定值)，以使得转矩和磁链具有相同的权值。但是这种方法不能满足系统不同性能指标下的不同需求。在文献[13]中，提出一种权值因子的优化算法，但其优化的结果仅仅只是使得转矩脉动最小。本文的的取值在参考文献[13]的理论基础上，结合自身模块的特点进行了一定的调整，取值为80。

式(9)中，V0,V1,...,V7表示的是逆变器8种开关状态下分别对应的电压空间矢量值，其所对应的电压空间矢量Vi(i=0,1,...,7)满足式：

(10)

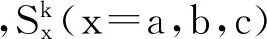
表1 逆变器工作状态、开关函数和相电压之间的关系

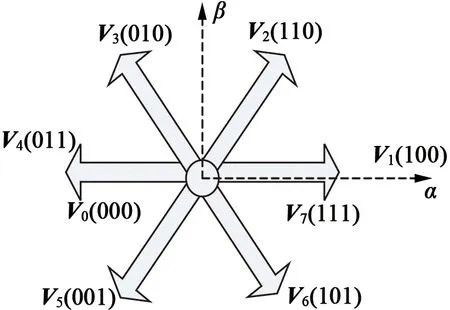
图2 逆变器状态与对应电压矢量关系图

较，选择最小的成本函数值所对应的开关矢量作为一个控制周期逆变器所对应的开关状态，因为相对于传统的直接转矩控制，模型预测控制所选定的开关矢量值是最优的，因而在减少转矩脉动上能达到一定的效果。

在每个采样周期内，分别对8种电压矢量所对应的成本函数值进行计算。对计算后的8个成本函数值进行比较，选择使成本函数值最小化所对应的开关状态作为此控制周期逆变器的开关状态。优化的整个过程如图3所示，其中x表示的是转矩和磁链的响应，Ts表示采样周期.假设如果在t(k)时刻的对应的x[t(k)]为最优值，在第t(k+1)时刻分别计算8种电压矢量所对应的成本函数值x[t(k+1)]，并将8个计算的成本函数值和x*(参考值)进行比较。其中与x*值最接近的xp4[t(k+1)]即为t(k+1)时刻的最优解。v4为t(k+1)时刻最优值所对应的电压矢量的控制信号。同理，t(k+2)时刻v3应选为最优控制信号。

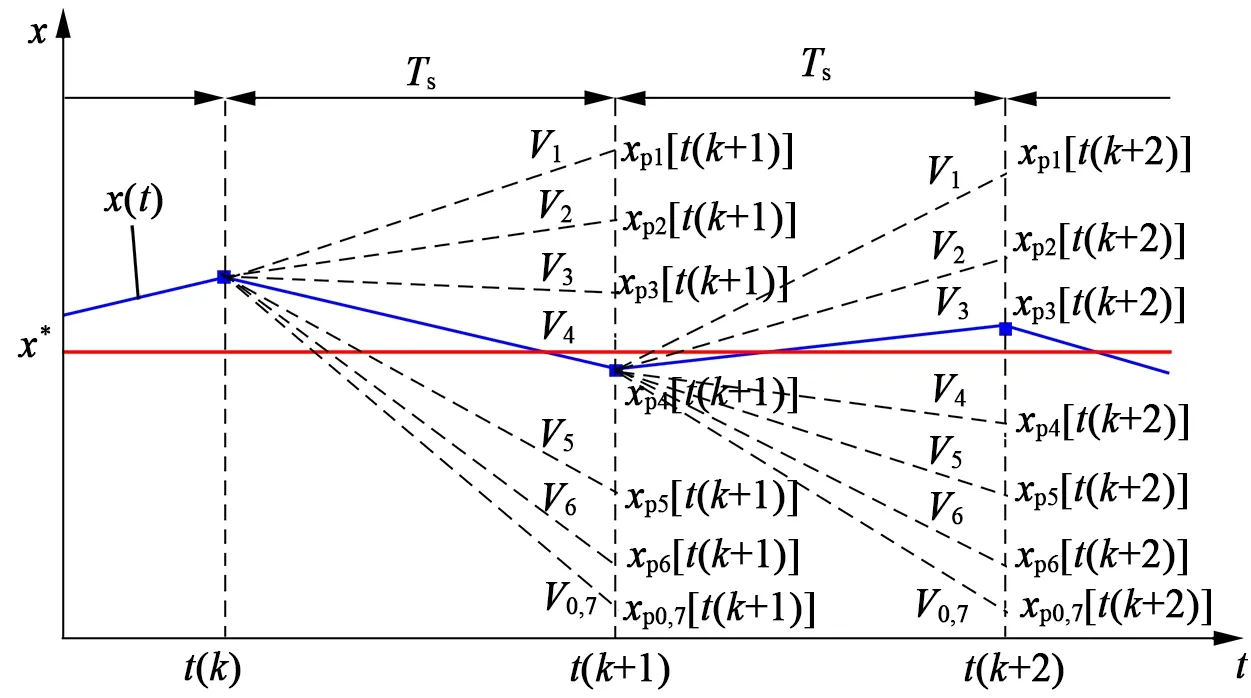
图3 模型预测控制的优化过程图

3 基于FCS-MPC系统下的弱磁控制原理

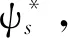
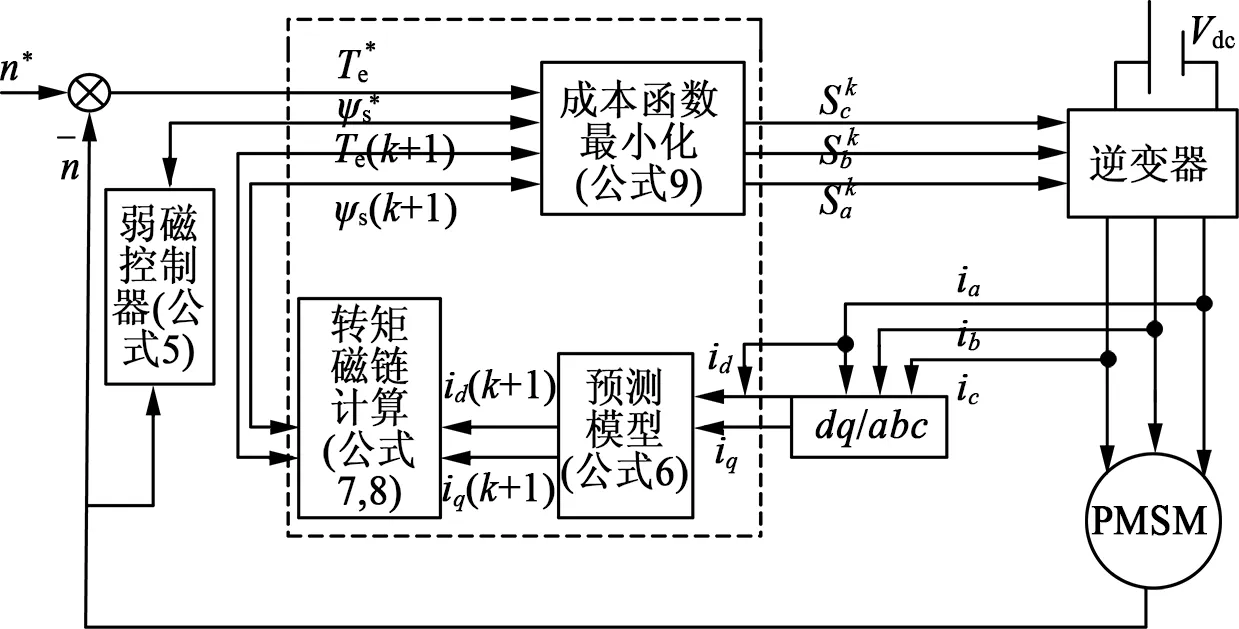
图4 PMSM弱磁FCS-MPC框图

4 仿真结果及分析

通过采用MATLAB软件分别建立了面贴式永磁同步电机在传统直接转矩控制下和在有限集模型预测控制系统下的弱磁模型。并将在两个模型下的弱磁控制效果图进行比较。仿真采用的电机模型为MATLAB自带电机模型，仿真过程中用到的电机参数如表2所示：仿真系统中给定参考速度为3 000 r/min,电机负载为1 N·m;0.05 s后，升速后的参考速度设定为5 000 r/min；0.1 s后，负载转矩值为2 N·m,Vdc的给定值为300 V。

表2 仿真所用永磁同步电机参数

图6、图7说明MPC弱磁系统下的三相电流比DTC弱磁系统下的三相电流在刚启动时的脉动更小。

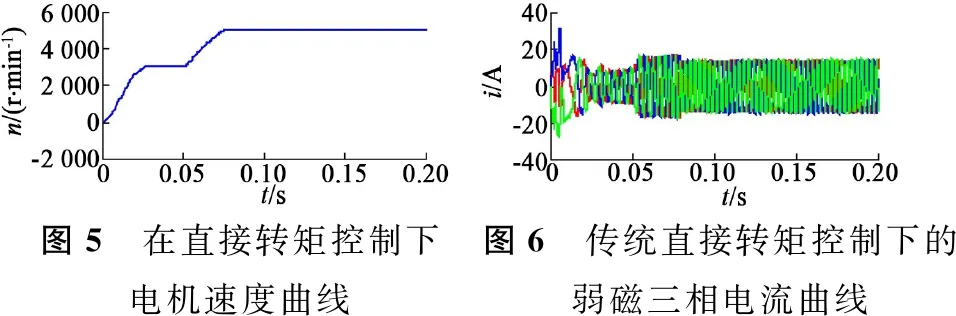
图5 在直接转矩控制下电机速度曲线图6 传统直接转矩控制下的弱磁三相电流曲线

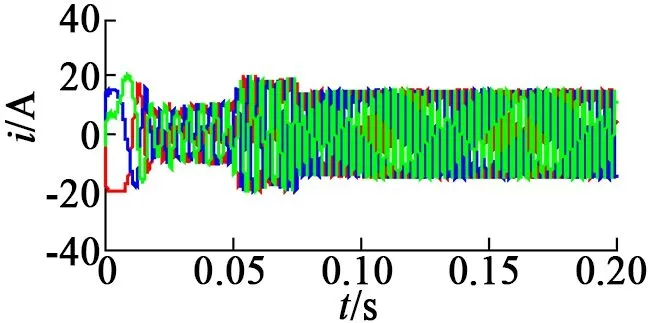
图7 使用有限集模型预测的弱磁三相电流曲线

图8、图9说明MPC下的弱磁控制系统在启动时d,q轴电流比DTC下的d,q轴电流更加稳定，0.1 s负载转矩加大以后DTC下的d轴电流的抖动比较大，而MPC下的d,q轴电流脉动明显较小。

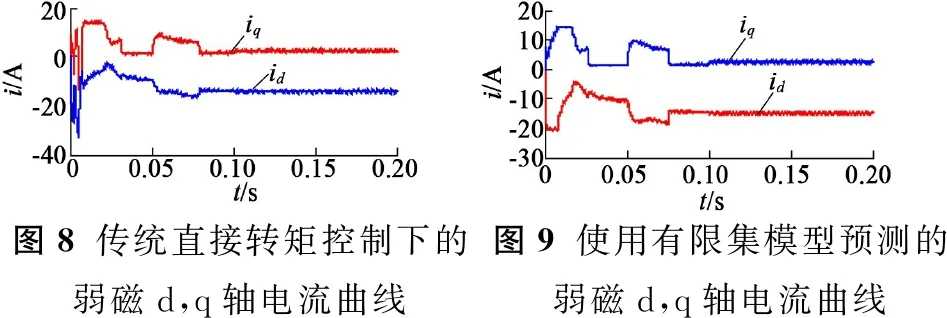
图8传统直接转矩控制下的弱磁d,q轴电流曲线图9使用有限集模型预测的弱磁d,q轴电流曲线

比较图10和图11说明，DTC下的转矩在刚开始启动时振荡较大，稳定后的脉动也大，而MPC系统的转矩在启动时较DTC稳定，转矩脉动小。

图10传统直接转矩控制下的弱磁转矩曲线图11使用有限集模型预测的弱磁转矩曲线

5 结 语

本文基于有限集模型预测对面贴式永磁同步电机的弱磁控制进行了理论分析。建立了使用有限集模型预测和传统的直接转矩下的同步电机弱磁控制模型，并且通过MATLAB/Simulink进行的仿真研究。仿真结果验证了该方法的优越性。与传统的直接转矩控制下的弱磁方法比较，显示出了本方法在抑制弱磁升速过程中转矩脉动以及电流脉动的优点，并且提高了系统的稳定性，为以后在永磁同步电机的驱动研究提供了参考。

[1] 张洪帅,王平,韩邦成.基于模糊PI模型参考自适应的高速永磁同步电机转子位置检测[J].中国电机工程学报,2014(12):1889-1896.

[2] 白玉成,唐小琦,吴功平.内置式永磁同步电机弱磁调速控制[J].电工技术学报,2011(9):54-59.

[3] 黄明明,林鹤云,金平,等.混合励磁同步电机驱动系统弱磁控制[J].电机与控制学报,2012,4(4):8-12.

[4] 陈宁,张跃,桂卫华,等.内埋式永磁同步电机驱动系统的弱磁控制[J].控制理论与应用,2013,6(6):717-723.

[5] XU Longya,ZHANG Yuan,GUVEN M K,et al.A new method to optimizeq-azis voltage for deep fluz weakening control of IPM machines based on single current regulator[C]//ICEMS 2008.IEEE,2008:2750-2754.

[6] KRISHNAN R.Control and operation of PM synchronous motor drives in the field-weakening region[C]//International Conference on Industrial Electronics,Control,and Instrumentation.IEEE,1993(2):745-750.

[7] 吴芳,万山明,黄声华.一种过调制算法及其在永磁同步电动机弱磁控制中的应用[J].电工技术学报,2010,1(1):58-63.

[8] MEYER M,BOCKER J.Optimum control for interior permanent magnet synchronous motors (ipmsm) in constant torque and flux weakening range[C]//12th International Power Electronics and Motion Control Conference,EPE-PEMC 2006.IEEE,2006:282-286.

[9] ZORDAN M,VAS P,RASHED M,et al.Field-weakening in high-performance PMSM drives: a comparative analysis[C]//Conference Record of 34th IAS Annual Meeting.IEEE,2000(3):1718-1724.

[10] 郑泽东,陈宁宁,李永东.基于模型预测控制的异步电机弱磁控制新方法[J].电工技术学报,2014,29(3):33-40.

[11] RODRIGUEZ J,CORTES P,KENNEL R,et al.Model predictive control:a simple and powerful method to control power converters[C]//IEEE 6th International Power Electronics and Motion Control Conference,IPEMC '09.IEEE,2009:41-49.

[12] RODRIGUEZ J,KENNEL R M,ESPINOZA J R,et al.High-performance control strategies for electrical drives:an experimental assessment[J].IEEE Transactions on Industrial Electronics,2012,59(2):812-820.

[13] ALIREZA DAVARI S,KHABURI D A,KENNEL R.An improved FCS-MPC algorithm for an induction motor with an imposed optimized weighting factor[J].IEEE Transactions on Power Electronics,2012,27(3):1540-1551.

Model Predictive Control Strategy for Permanent Magnet Synchronous Motor Based on Flux-Weakening Speed Rise

YUYu-ting1,TENGQing-fang1,BAIJian-yong2,HANSi-yuan1

(1.Lanzhou Jiao Tong University,Lanzhou 730070,China;2.Jinan Railway Signal Depot in Qingdao,Qingdao 266000,China)

For permanent magnet synchronous motor in the process of flux weakening prone to the problem of torque ripple, finite set of model predictive control method is designed on the basis of flux weakening control. Finite set of model predictive control algorithm' realization need to use the limited switch rectifier characteristics, and motor mathematical model to predict the future state of the system. At the same time, set up the target function, using traversing method to optimize the best switch state of the system. In the end , use the best switch state selected by target function as control signal , so that the system stability is better . Simulation and experimental results show that the proposed control strategy reduces torque ripple of permanent magnet synchronous motor and provides better robustness.

surface mounted permanent magnet synchronous motor; flux-weakening control; constant magnetic linkage control; finite set of model predictive control; stability

2016-03-12

国家自然科学基金项目(61463025)；人社部2015留学人员科技活动择优资助项目

吴小江(1986-)，硕士，高级工程师，研究方向为电机结构、电磁设计以及电机控制。

TM341:TM351

A

1004-7018(2016)12-0044-04