基于漏斗试样的C250钢高温扭转低周疲劳行为

赵兴华， 蔡力勋,*， 包陈， 江志华

1.西南交通大学 力学与工程学院 应用力学与结构安全四川省重点实验室， 成都 610031 2.中航工业北京航空材料研究院， 北京 100095

基于漏斗试样的C250钢高温扭转低周疲劳行为

赵兴华1， 蔡力勋1,*， 包陈1， 江志华2

1.西南交通大学 力学与工程学院 应用力学与结构安全四川省重点实验室， 成都 610031 2.中航工业北京航空材料研究院， 北京 100095

C250钢的扭转疲劳破坏是其主要失效形式之一。为了获得航空材料C250钢的扭转疲劳特性，并消除等直圆棒试样在扭转试验中产生的弊端，依据漏斗试样完成了C250钢在3种高温(150、200、350 ℃)环境下的扭转低周疲劳试验，获得了在扭转低周疲劳下的扭矩-名义扭转角曲线。基于试验结果，利用FAT方法分析得到了C250钢在3种高温环境下的材料循环本构关系，利用该循环本构关系对漏斗试样进行三维扭转有限元分析，获得漏斗根部剪切应力与扭矩之间的转换公式及漏斗根部剪切应变与名义扭转角之间的转换公式。基于以上试验与分析方法，得到了材料的剪切应变幅-倍循环次数曲线、剪切应力幅-循环分数曲线以及剪切应力-剪切应变的稳定滞回线，发现材料呈现出循环软化特性，并基于Manson-Coffin模型对材料寿命进行了分析。

扭转低周疲劳； 有限元辅助测试方法； C250钢； 漏斗试样； 扭转特性； Manson-Coffin模型

扭转疲劳问题广泛存在于汽车、火车轮轴，发动机曲轴及航空领域的各种凸轮轴、齿轮轴等关键部件中。目前，对扭转疲劳的研究多集中于高周应力疲劳[1-4]，对低周应变疲劳的研究特别是高温低周疲劳研究[5-6]相对较少。传统扭转低周疲劳通过对等直试样施加循环扭应变完成[7-10]。根据平面假设和von Mises等效原理，扭转的循环应力应变可以直接转换到轴向循环的应力应变，但等直试样的扭转试验仍存在若干问题。首先，等直试样细长比相对较大，要达到足够的剪应变需要有很大的扭转角度，这样不仅大大降低了加载频率，也容易影响应变控制下引伸计的夹持稳定性；其次，在高温条件下由于存在增长的高温引伸加持部件，采用等直试样使得试验机作动器总扭转角更大，试验周期更长，循环稳定性降低；另外，扭转疲劳需了解材料循环本构关系[11-14]，而按传统获取循环本构关系的方法则需要另外完成较多单轴试样的轴向疲劳试验，使得扭转疲劳试验不易实现分析。

C250钢具有较高强度和良好延性，被广泛应用于水翼船支架等民用领域及飞机起落架、各种轴类零件、铀浓缩用离心分离机的旋转桶、导弹壳体、火箭发动机壳体等领域[15-16]。此类构件承受扭转疲劳或弯扭疲劳而破坏，因此材料扭转疲劳行为的研究对结构安全设计有重要意义。

采用漏斗试样进行低周扭转疲劳研究，可以有效解决等直圆棒试样扭转角过大导致应变引伸计存在的应变测控稳定性问题；同时，由于危险截面为漏斗根部的唯一截面，其高温均匀性容易保证。本文采用蔡力勋研究组发展的FAT(Finite-element-analysis Aided Testing)方法[17-18]，以扭转疲劳试验获得的循环载荷-角度曲线为判据，以材料单轴应力-应变关系为初始本构关系进行迭代计算，可基于漏斗试样循环试验关系得到材料循环本构关系，实现名义测试扭应变和漏斗根部横截面径向剪切应力、剪切应变的转换，进而可以实现扭转低周疲劳行为的分析。

1 试验条件

试验材料为C250马氏体不锈钢，图1给出了C250钢单向拉伸试样尺寸，图2是由该试样在不同温度下得到的单向拉伸应力-应变曲线，t为温度，由图2可知，在试验温度范围内材料应力-应变(σ-ε)关系受温度影响较小。C250钢的主要化学成分见表1。

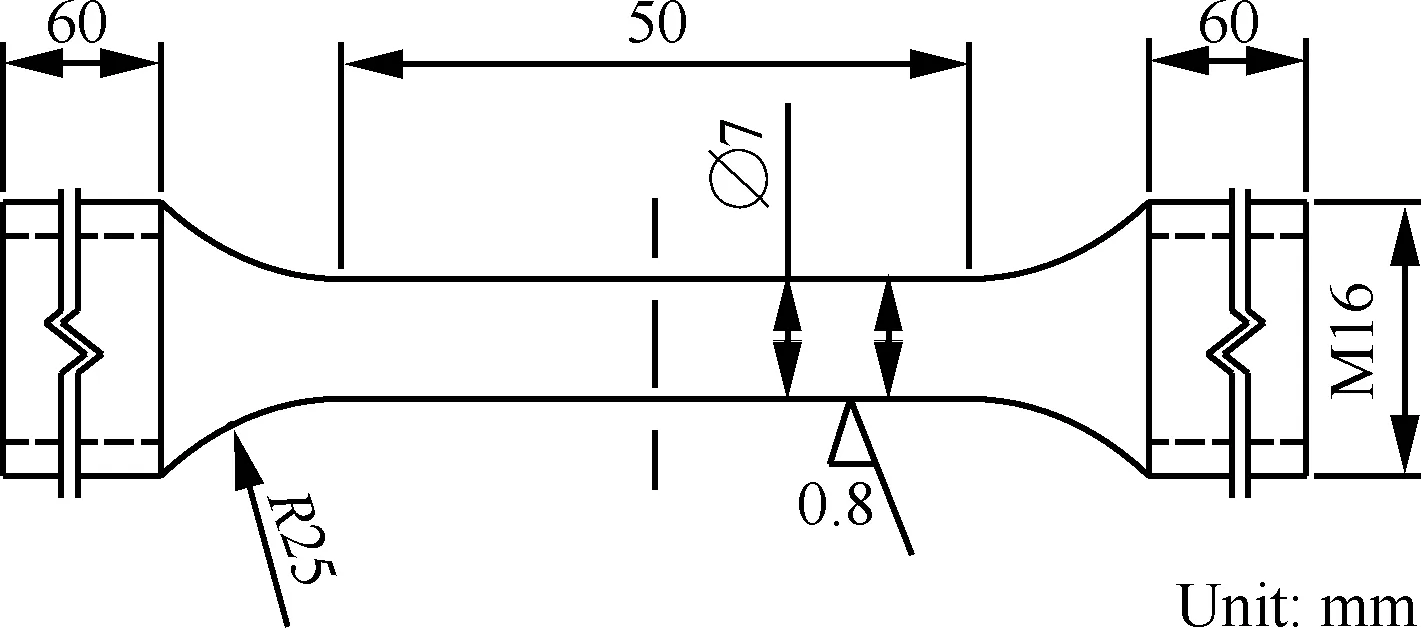
图1 拉伸试样尺寸

Fig.1 Size of tensile specimen

图2 C250钢在不同温度下的单向拉伸σ -ε曲线

Fig.2 Uniaxial tensile stress-strain curves of C250 steel at different temperatures

表1 C250钢的主要化学成分

低周疲劳试验采用图3所示的两级漏斗试样，漏斗根部直径为6 mm，漏斗半径为18 mm，漏斗两侧的4 mm等直段用于夹持引伸计，试样经热处理后加工成形。

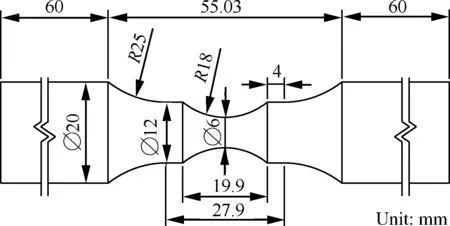
图3 扭转试样尺寸

Fig.3 Size of torsional specimen

试验在MTS809(最大拉力250 kN/最大扭矩2 000 N·m)电液伺服材料试验机上完成，传感器为0.5级精度。试验为等效应变幅比值R=-1的对称扭转，温度t分别为150、200、350 ℃。高温炉(MTS653)控制精度为±1 ℃，引伸计测量范围内的材料温度误差为±5 ℃。试验中采用的拉扭引伸计为MTS632.68F，标距L=25 mm，精度0.5级。该引伸计在出厂时采用半径r=12.5 mm 的圆棒标准试样进行扭应变标定，因所测试样测量位置半径a=6 mm，须对剪切应变进行转换，转角间的关系式为

(1)

式中：φn为名义扭转角(引伸计实测值)；φt为试样标距内的真实扭转角。

2 FAT方法获取材料循环本构关系

有限元辅助测试(FAT)方法是以试验结果为判据，基于有限元测试手段，对初始应力-应变关系进行迭代修正的过程，其分析流程如图4所示。图中T-φn为载荷-名义扭转角试验曲线，σe-εe为等效应力-等效应变曲线，i为迭代次数。

基于有限元分析软件ANSYS，选用Solid186单元建立图5所示的三维实体模型并进行网格划分，并通过比例关系适当增加漏斗根部网格密度，模型单元总量在综合分析收敛性和计算耗时的条件下进行控制。

图4 FAT方法流程图

Fig.4 Flowchart of FAT method

图5 漏斗试样的有限元模型

Fig.5 Finite element model of funnel specimen

为了消除扭矩施加时的应力集中影响，采用无质量刚性梁单元(MPC184)将模型端面节点与端面外一控制节点连接起来，然后在控制节点施加扭矩，从而实现对试样端面均匀施加扭矩。施加柱坐标系下边界条件，对控制节点施加轴向和径向约束，另一端采取固定约束。

图6给出了3种温度下扭转低周疲劳试验获得的T-φn曲线。由图6可知，3种温度下的T-φn曲线几乎重合，说明在该研究范围内温度对材料的影响非常小。因此，任选其中一条T-φn曲线作为判据，利用FAT方法反算材料的高温循环等效应力-等效应变关系。

图7给出了150 ℃下3次迭代所得的T-φn曲线与试验得到的T-φn曲线的对比图。由图7知，经过3次迭代计算后，有限元输出的结果已经与试验结果完全重合，图中迭代结果的外延部分不在本文研究范围内，本文只考虑试验数据范围内转换公式的获得。

图6 3种温度下的T-φn曲线

Fig.6 T-φncurves at three kinds of temperatures

图7 试验与3次迭代计算得到的T-φn曲线(t=150 ℃)

Fig.7 T-φncurves by three times iterative calculation and test (t=150 ℃)

因为3种温度下的T-φn曲线重合，所以200、350 ℃下的迭代结果与150 ℃相同，故可以只进行一种温度下的迭代计算。150 ℃时的T-φn曲线经过3次迭代得到的漏斗根部的σe-εe曲线如图8所示。

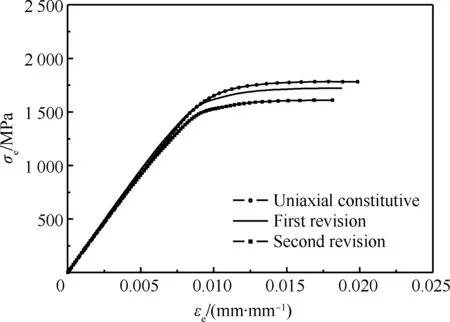
图8 3次迭代计算的漏斗根部σe-εe曲线(t=150 ℃)

Fig.8 σe-εecurves by three times iterative calculation of funnel root (t=150 ℃)

3 转换公式

假定材料满足von Mises等效原则，对于等直圆棒试样的纯扭转问题，等效应变与剪切应变、等效应力与剪切应力关系满足：

(2)

式中：γ为剪切应变；τ为剪切应力。而对于漏斗试样，由于约束条件的改变，依据T-φn曲线不能直接获得漏斗根部的扭转应力状态，因此需要通过有限元重新确定。

将FAT方法迭代得到的循环本构关系代入图5所示的有限元模型进行扭转计算，可以获得图9(a)所示的C250钢漏斗试样标距(25 mm)范围内名义扭转角φn与漏斗根部剪切应变γ之间的关系，剪切应变的表达式为

(3)

式中：p1=10.426；p2=-6.258 9；p3=89.833；p1～p3为表达式系数。同理可以得到扭矩T与漏斗根部剪切应力τ之间的关系(见图9(b))：

τ=f(T)=k1+k2T+

k3T2+k4T3+k5T4+k6T5

(4)

式中：k1=-4.126 2；k2=25.625；k3=-0.459 28；k4=0.024 302；k5=-5.023 2×10-4；k6=2.870 8×10-6。剪切应变与等效应变、剪切应力与等效应力之间仍然满足式(2)。

图9 试样标距范围内的γ-φn和τ-T曲线

Fig.9 Curves of γ-φnand τ-T within gauge length of specimen

4 试验结果与分析

图10给出了不同温度下扭转低周疲劳试验的σe-εe曲线与单调拉伸σe-εe曲线对比情况。由图可见，3种温度下扭转低周疲劳得到的σe-εe试验数据点基本重合，且明显低于单调应力-应变曲线，说明C250钢呈现出循环软化特性。图11给出了扭转低周疲劳3种温度下的剪切应变幅与倍寿命(Δγ/2-2Nf)曲线。鉴于一个循环的拉、压阶段经历了两次等损伤过程，故采用倍寿命，即2Nf来表征应力、应变幅与全程寿命中的低周疲劳损伤累积的关联性。由图11可知，不同温度下的Δγ/2-2Nf曲线几乎重合，且近似满足幂律关系，说明研究范围内温度对C250钢的疲劳性能影响较小。

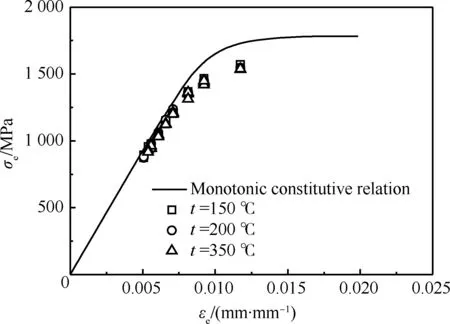
图10 3种温度下扭转低周疲劳试验所得σe-εe曲线与单调本构曲线的对比

Fig.10 Contrast of monotonic constitutive curve and σe-εecurves of torsional low cycle fatigue test at three different temperatures

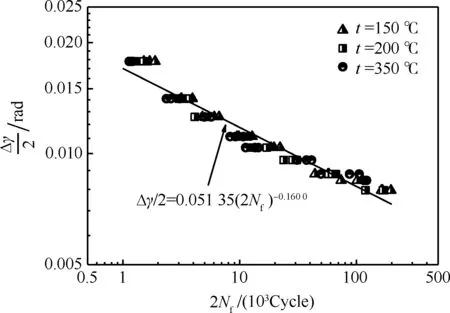
图11 3种温度下的Δγ/2-2Nf曲线

Fig.11 Δγ/2-2Nfcurves at three different temperatures

图12给出了3种温度不同等效应变幅εe下的剪切应力幅Δτ/2与循环分数N/Nf的关系。图中，材料剪切应力幅随循环分数增大而减小，当应变幅较≥8 000 με时减小的趋势明显增大，说明材料表现出循环软化的特性，且随应变幅增大软化现象逐渐增强。这与图10所示的软化特性完全吻合。

图12 3种温度不同等效应变幅下的Δτ/2-N/Nf

曲线

Fig.12 Δτ/2-N/Nfcurves of different equivalent amplitude at three different temperatures

图13给出了3种温度下不同应变幅下的剪切稳定滞回线(τ-γ曲线)，由图13可知，3种温度的稳定滞回线形状基本一致，且当应变幅<8 000 με 时滞回环非常小。这是因为C250钢的强度很高，低周疲劳时塑性应变所占比重很小所致。

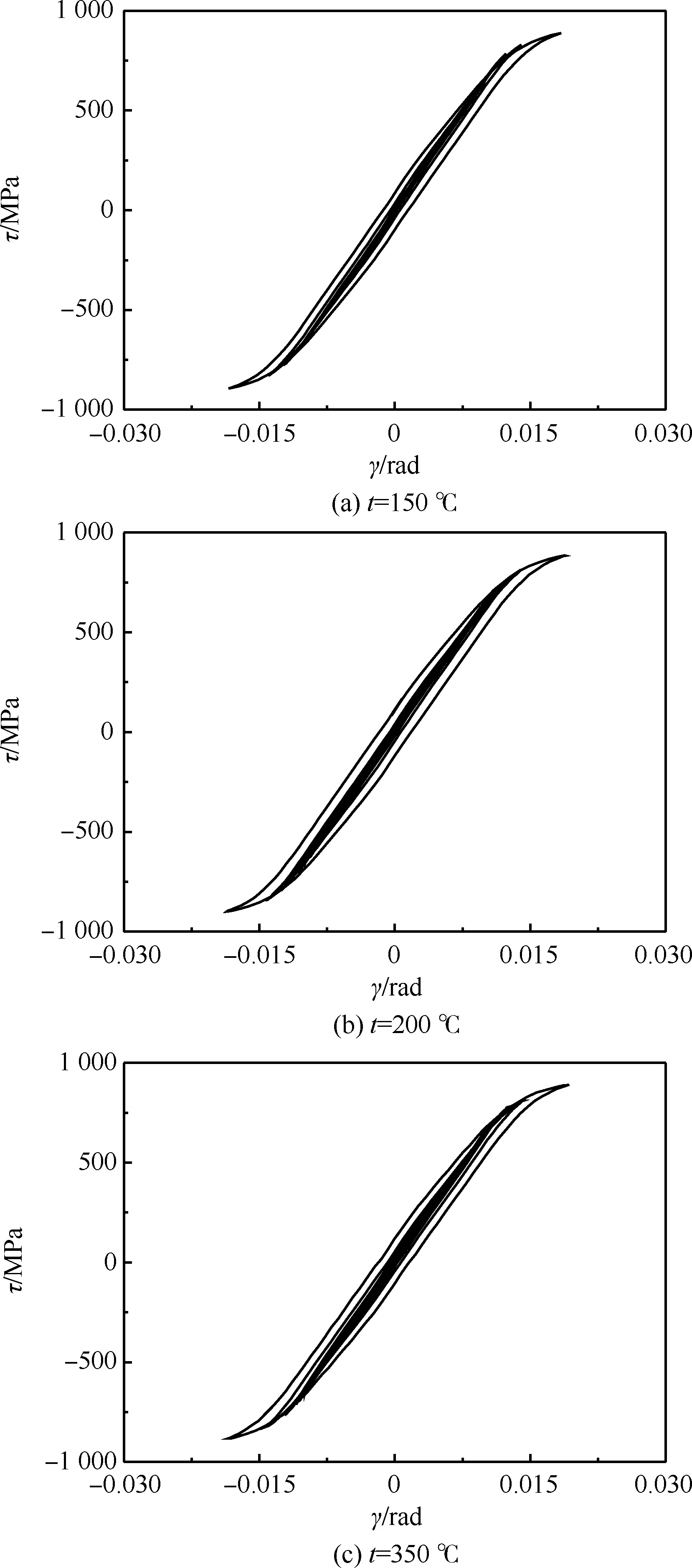
图13 不同应变幅下的滞回线

Fig.13 Hysteresis loops at different strain amplitudes

一般情况下，大部分材料的扭转应变疲劳满足式(5)所示的Manson-Coffin模型[19-20]：

(5)

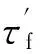
根据剪切应变的弹、塑性分解方法，式(5)可以分解为

(6)

(7)

然而也有部分特殊的材料的扭转低周疲劳不满足单一的Manson-Coffin模型，而是表现出了分段特性，需要用两个不同的Manson-Coffin公式才能描述[21-22]，本文中的材料就表现出这种特性。

图14(a)给出了剪切应力幅Δτ/2与倍寿命2Nf关系曲线，其很好的满足式(6)。图14(b)给出了剪切塑性应变幅Δγp/2与倍寿命2Nf关系曲线。

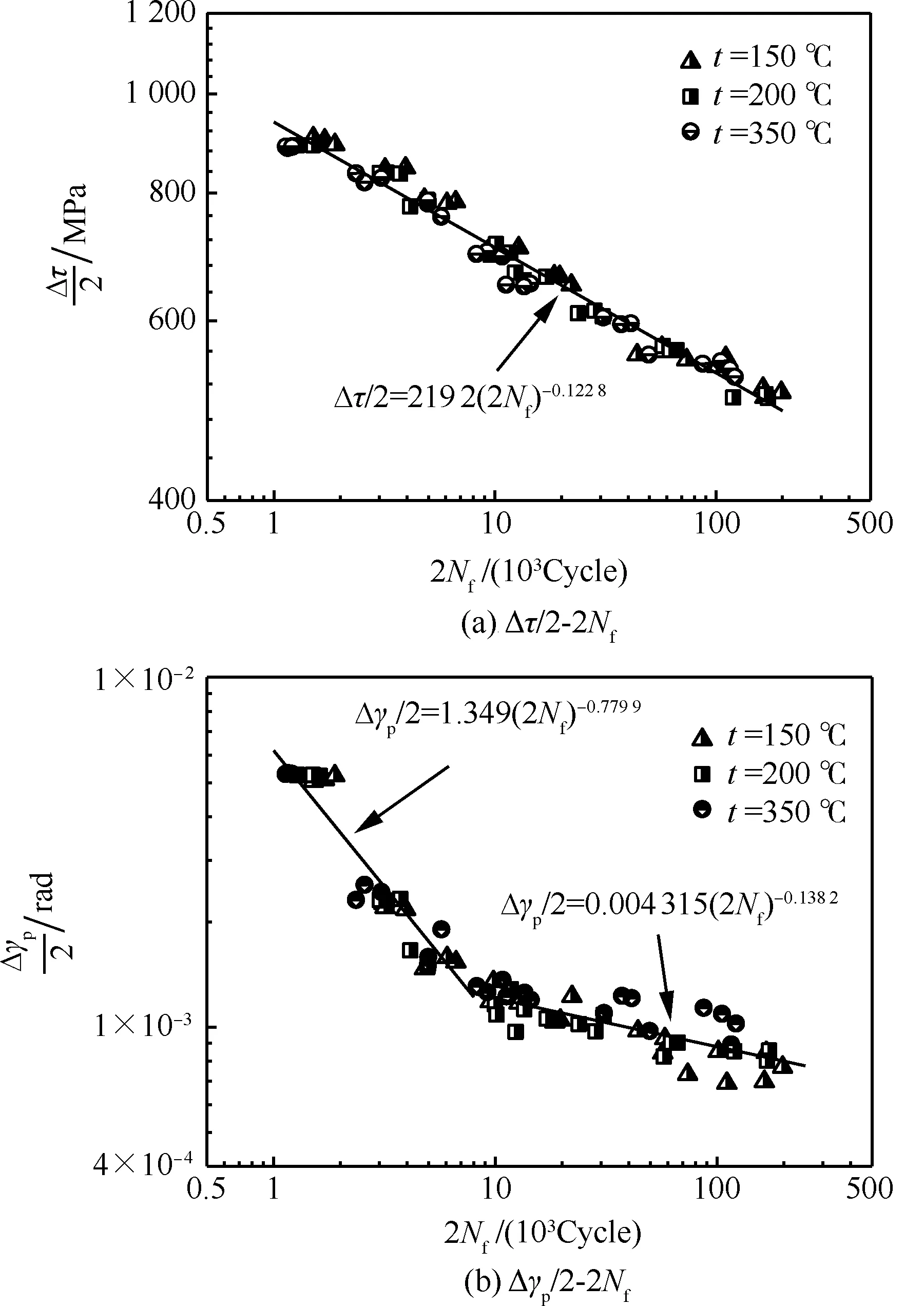
图14 Δτ/2-2Nf和Δγp/2-2Nf曲线

Fig.14 Curves of Δτ/2-2Nfand Δγp/2-2Nf

由图14(b)易见，式(7)不能很好地描述曲线的变化趋势。这是因为，图11中材料的Δγ/2-2Nf曲线虽基本满足幂律关系，但表现出两端寿命偏高的特点。结合前面的分析，该C250钢低周扭转疲劳在小应变幅下的塑性应变占比非常小，因此Δγ/2-2Nf曲线的微小偏离在塑性应变中被放大，呈现出分段式的幂律关系，其分段拟合的表达式如图14(b)中所示。考虑到材料的特殊性，使用总剪切应变-倍循环次数关系进行寿命预测效果更好。

5 结 论

1) 提出了一种用于高温扭转疲劳行为研究的试验方法，该方法以扭转低周疲劳T-φn曲线为基础，结合FAT方法可以获得材料的循环本构关系；基于循环本构关系对漏斗形试样进行三维有限元分析，获得漏斗试样根部剪切应力和剪切应变的转换公式以及循环本构关系的参数,进而可获得材料扭转低周疲劳行为规律。

2) 针对C250试样提出了测试应变和扭矩，获得了试样漏斗根部的剪切应力、应变的转换公式，获得了C250钢的Δγ/2-2Nf低周疲劳特性曲线，且曲线较好地满足幂律关系。

3) 分析了C250材料的剪切应变幅随循环次数的演化规律，当材料在≥8 000με应变幅时表现出较明显的循环软化特性。

4) 利用Manson-Coffin寿命预测模型对试验结果所进行的分析表明，材料的塑性剪切应变幅与倍寿命关系曲线存在明显拐点，不符合单一Manson-Coffin关系。

[1] DAVOLI P, BERNASCONI A, FILIPPINI M, et al. Independence of the torsional fatigue limit upon a mean shear stress[J]. International Journal of Fatigue, 2003, 25(6): 471-480.

[2] 包陈, 蔡力勋, 钟斌. 两种合金钢的高温扭转疲劳性能[J]. 材料研究学报, 2007, 21(增刊): 2-5. BAO C, CAI L X, ZHONG B. Torsional fatigue properties of two alloy steels at elevated temperature[J]. Chinese Journal of Materials Research, 2007, 21(Suppl.): 2-5 (in Chinese).

[3] 金磊, 夏慧琴. 扭转疲劳试验的探索性研究[J]. 材料工程, 1997(6): 34-35. JIN L, XIA H Q. Eploring research on torsional fatigue properties in stainless steel, aluminum alloy and structural steel[J]. Journal of Materials Engineering, 1997(6): 34-35 (in Chinese).

[4] 钟斌, 何玉怀, 苏彬. 1Cr11Ni2W2MoV和16Ni3CrMoE两种钢的高温扭转疲劳性能研究[J]. 机械强度, 2004, 26(增刊): 169-171. ZHONG B, HE Y H, SU B. High temperature torque fatigue properties of 1Cr11Ni2W2MoV and 16Ni3CrMoE[J]. Journal of Mechanical Strength, 2004, 26(S): 169-171 (in Chinese).

[5] 杨晓光, 黄佳, 王井科, 等. 定向凝固镍基高温合金缺口低循环疲劳性能及寿命预测[J]. 航空学报, 2013, 34(7): 1596-1604. YANG X G, HUANG J, WANG J K, et al. Properties and life prediction of low cycle fatigue behavior on notched ds ni-based superalloy[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(7): 1596-1604 (in Chinese).

[6] 丁智平, 曾军, 陈吉平. 镍基单晶合金多轴非对称循环加载应力弱化损伤与低周疲劳研究[J]. 航空学报, 2013, 34(12): 2768-2776. DING Z P, ZENG J, CHEN J P. Study on stress-weakening damage and low cycle fatigue of Ni-based single crystal superalloy under multiaxial asymmetric loading[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(12): 2768-2776 (in Chinese).

[7] 赵廷仕, 刘敦康, 纪惠君. 35钢低周扭转应变疲劳的研究[J]. 金属学报, 1987, 23(2): 156-157. ZHAO T S, LIU D K, JI H J. Low cycle fatigue of steel 35 under torsional strain[J]. Acta Metallurgica Sinica, 1987, 23(2): 156-157 (in Chinese).

[8] 孙永健, 程琴, 唐雪艳. 变工况下汽轮机转子热应力分析及低周疲劳寿命计算[J]. 机械工程学报, 2013, 49(2): 28-36. SUN Y J, CHENG Q, TANG X Y. Analysis of thermal stress and calculation of low-cycle fatigue life for a steam turbine under variable operating conditions[J]. Journal of Mechanic Engineering, 2013, 49(2): 28-36 (in Chinese).

[9] BROWN M W, MILLER K J. High temperature low cycle biaxial fatigue of two steels[J]. Fatigue & Fracture of Engineering Materials & Structures, 1979, 1(2): 217-229.

[11] 杨丽红, 何蕴增, 吴国辉, 等. 基于扭转试验的大变形本构关系分析[J]. 哈尔滨工程大学学报, 2007, 27(6): 816-820. YANG L H, HE Y Z, WU G H, et al. Analysis of large strain constitutive relationship based on torsion test[J]. Journal of Harbin Engineering University, 2007, 27(6): 816-820 (in Chinese).

[12] 杨丽红. 基于实心圆轴扭转实验的大变形本构关系研究[D]. 哈尔滨: 哈尔滨工程大学, 2005: 22-35. YANG L H. Research on large deformation constitutive relationship based on cylindrical shaft torsion test[D]. Harbin: Harbin Engineering University, 2005: 22-35 (in Chinese).

[13] 何蕴增, 邹广平. 实心圆轴扭转测定本构关系的概念和方法[J]. 实验力学, 2003, 18(3): 426-432. HE Y Z, ZOU G P. The concept and method for determining the constitutive law of materials by torsion test with cylindrical specimens[J]. Journal of Experimental Mechanics, 2003, 18(3): 426-432 (in Chinese).

[14] 何蕴增, 邹广平. 实心圆试件扭转试验确定大应变本构关系[J]. 力学学报, 2001, 33(6): 828-833. HE Y Z, ZOU G P. Determine finite-strain stress-strain relationship by torsion test with cylindrical specimens[J]. Acta Mechanica Sinica, 2001, 33(6): 828-833 (in Chinese).

[15] DECKER R F, FLOREEN S. Maraging steels—the first 30 years[J]. Maraging Steels: Recent Developments and Applications, 1988: 1-38.

[16] 姜越, 尹钟大, 朱景川, 等. 超高强度马氏体时效钢的发展[J]. 特殊钢, 2004, 25(2): 1-5. JIANG Y, YIN Z D, ZHU J C, et al. Development of ultra-high strength maraging steel[J]. Special Steel, 2004, 25(2): 1-5 (in Chinese).

[17] 姚迪, 蔡力勋, 包陈, 等. 基于试验与有限元耦合技术的延性材料全程单轴本构关系获取方法[J]. 固体力学学报, 2014, 35(3): 226-240. YAO D, CAI L X, BAO C, et al. Determination of stress-strain curve of ductile materials by testing and finite element coupling method[J]. Chinese Journal of Solid Mechanics, 2014, 35(3): 226-240 (in Chinese).

[18] 陈辉, 蔡力勋, 姚迪, 等. 基于小尺寸材料试验与有限元分析的耦合方法获取材料力学性能[J]. 机械强度, 2014, 36(2): 187-192. CHEN H, CAI L X, YAO D, et al. Obtaining material mechanical properties by coupling method based on tests of small size specimens and finite element analysis[J]. Journal of Mechanical Strength, 2014, 36(2): 187-192 (in Chinese).

[19] MCCLAFLIN D, FATEMI A. Torsional deformation and fatigue of hardened steel including mean stress and stress gradient effects[J]. International Journal of Fatigue, 2004, 26(7): 773-784.

[20] SHAMSAEI N, FATEMI A. Deformation and fatigue behaviors of case-hardened steels in torsion: experiments and predictions[J]. International Journal of Fatigue, 2009, 31(8): 1386-1396.

[21] WANG X G, GAO Z L, QIU B X, et al. Multi-axial fatigue of 2024-T4 aluminum alloy[J]. Chinese Journal of Mechanical Engineering, 2011, 24(2): 195-201.

[22] JAHED H, VARVANI-FARAHANI A. Upper and lower fatigue life limits model using energy-based fatigue properties[J]. International Journal of Fatigue, 2006, 28(5): 467-473.

赵兴华 男， 硕士研究生。主要研究方向： 材料的疲劳与断裂力学。

E-mail: xinghua19881105@126.com

蔡力勋 男， 教授， 博士生导师。主要研究方向： 材料本构关系、疲劳与断裂力学。

Tel: 028-87600850

E-mail: lix_cai@263.net

Received： 2014-12-26； Revised： 2015-01-16； Accepted： 2015-02-05； Published online： 2015-02-12 10：41

URL： www.cnki.net/kcms/detail/11.1929.V.20150212.1041.004.html

Foundation items： National Natural Science Foundation of China (11472228); Sichuan Youth Science and Technology Innovation Team (2013TD0004)

*Corresponding author. Tel.： 028-87600850 E-mail:lix_cai@263.net

Torsional low-cycle fatigue behavior of C250 steel using funnelspecimens at elevated temperature

ZHAO Xinghua1, CAI Lixun1,*, BAO Chen1, JIANG Zhihua2

1.AppliedMechanicsandStructureSafetyKeyLaboratoryofSichuanProvince,SchoolofMechanicsandEngineering,SouthwestJiaotongUniversity,Chengdu610031,China2.AVICBeijingInstituteofAeronauticalMaterials,Beijing100095,China

Torsional fatigue rupture is one of C250 steel’s main failure forms. In order to obtain torsional fatigue characteristics of C250 steel and eliminate the disadvantages of straight rod specimen, a series of torsional fatigue tests on C250 steel at three different elevated temperatures, 150, 200, 350 ℃ using funnel specimens has been carried out, and the curves of nominal torque-nominal torsional angle for C250 steel at each temperature are given. Based on the test results and finite-element-analysis aided testing (FAT) method, the effective cyclic constitutive relationships of C250 steel at those temperatures have been obtained. By using these effective cyclic constitutive relationships, 3D finite element analyses of funnel specimen under torsion are used to reveal the transforming relationship between the torque and shear stress at the root of funnel specimen, as well as the relationship between the nominal torsional angle and shear strain at the root of funnel specimen. On the basis of those test and analyzing methods, the curves of shear stress-times cycles、shear strain amplitude-cyclic fraction and stable hysteresis loop of shear stress-shear strain have been obtained. The material shows cyclic softening by the analysis of the low-cycle fatigue behavior, and the typical Manson-Coffin model is employed to predict the torsional fatigue life of C250 steel at three different elevated temperatures.

torsional low-cycle fatigue; FAT method; C250 steel; funnel specimen; torsional behavior; Manson-Coffin mode

2014-12-26；退修日期：2015-01-16；录用日期：2015-02-05； < class="emphasis_bold">网络出版时间：

时间： 2015-02-12 10：41

www.cnki.net/kcms/detail/11.1929.V.20150212.1041.004.html

国家自然科学基金 (11472228)； 四川省青年科技创新研究团队 (2013TD0004)

.Tel.： 028-87600850 E-mail: lix_cai@263.net

赵兴华, 蔡力勋, 包陈, 等. 基于漏斗试样的C250钢高温扭转低周疲劳行为[J]. 航空学报, 2016, 37(2): 617-625. ZHAO X H, CAI L X, BAO C, et al. Torsional low-cycle fatigue behavior of C250 steel using funnel specimens at elevated temperature[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(2): 617-625.

http://hkxb.buaa.edu.cn hkxb@buaa.edu.cn

10.7527/S1000-6893.2015.0042

V216.3； O348

： A

： 1000-6893(2016)02-0617-09

*