一类分数阶复杂网络系统的有限时间同步控制

毛北行，王战伟

郑州航空工业管理学院数理系，河南郑州 450015



Received：2015-05-17；Accepted：2015-09-23

Foundation：National Natural Science Foundation of China(11404291); Key Scientific Research Project of Colleges and Universities of Henan Province(15B110011)

† Corresponding author：Associate professor Mao Beixing. E-mail: bxmao329@163.com

Citation：Mao Beixing, Wang Zhanwei. Finite-time synchronization control of a class of fractional-order complex network systems[J]. Journal of Shenzhen University Science and Engineering, 2016, 33(1): 96-101.(in Chinese)

【应用数学 / Applied Mathematics】

一类分数阶复杂网络系统的有限时间同步控制

毛北行，王战伟

郑州航空工业管理学院数理系，河南郑州 450015

摘要：研究一类分数阶复杂网络系统的有限时间混沌同步问题，基于Lyapunov稳定性理论和分数阶微积分的相关理论，给出控制律的设计，得到了系统取得有限时间同步的充分条件，估算了系统取得同步所需的时间．研究结果表明，一定条件下分数阶复杂网络混沌系统是有限时间同步的，仿真结果验证了方法的可行性.

关键词：分数阶系统；有限时间；混沌同步；复杂网络；误差系统；控制

自Pecora提出驱动—响应同步方法以来，混沌控制与混沌同步及其应用已逐渐成为研究热点[1-5]．在实际应用中，有时希望同步过程在有限时间内完成，达到所谓“有限时间同步”[6-8]．采用不同的控制方法可达到混沌系统的有限时间同步．文献[9]研究Lurie混沌系统的有限时间同步，给出系统实现快速同步的充分条件；文献[10]研究一类分数阶不确定系统的有限时间鲁棒混沌同步，给出控制律的设计和实现快速同步的条件．本文研究一类分数阶复杂网络系统的有限时间混沌同步问题，基于Lyapunov稳定性理论及分数阶微积分的相关理论，给出实现有限时间同步的充分条件，仿真结果验证该方法是可行的．

1预备知识

定义1[11]Caputo分数阶导数定义为

n-1<α

考虑如下分数阶复杂网络系统

(1)

其中， i表示系统节点， 1≤i≤N， N为网络的节点连接个数； j表示系统连接节点； f(·)是连续可微的非线性函数； xi(t)=[xi1(t),xi2(t),…,xin(t)]T∈Rn是节点i的状态变量； xi1(t),xi2(t),…,xin(t)是状态变量 xi(t)的各个分量， n为状态变量的维数； C=(cij)N×N为N×N阶的耦合配置矩阵， cij为耦合配置矩阵的耦合矩阵元素； A为内部耦合矩阵，反映了网络的拓扑结构和节点的耦合强度．

以系统(1)作为驱动系统，设计响应系统为

Dαyi(t)=f(yi(t))+

(2)

其中， yi和yj为响应系统状态变量；ui(t)为控制器．

定义系统误差ei(t)=yi(t)-xi(t)， 上述两式相减得误差系统方程为

Dαei(t)=f(yi)-f(xi)+

(3)

2主要结果

根据引理1得

(4)

其中， ρ=min{ki(i=1,2,…,n)}, v=min{li(i=1,2,…,n)}．

根据不等式(4)得

因此

(5)

对式(5)两边从0到T积分， e(T)=0, T=max{ti(i=1,2,…,n)}, 得

考虑如下分数阶不确定复杂网络系统

Dαxi(t)=f(xi(t))+Δf(xi(t))+

(6)

其中，Δf(xi(t))表示来自驱动系统的不确定项.

以系统(5)作为驱动系统，设计响应系统

Dαyi(t)=f(yi(t))+Δf(yi(t))+

(7)

其中，Δf(yi(t))表示来自响应系统的不确定项.

定义系统误差ei=yi-xi， 则得到误差系统为

Dαei(t)=f(yi)-f(xi)+Δf(yi)-Δf(xi)+

(8)

定理2选取系统的控制器为

Dα-1[kiei(t)+(γ+

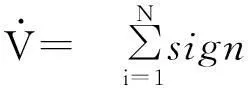
Δf(yi(t))-Δf(xi(t))+

根据引理1得

以下证明同定理1，在此从略．

3数值仿真

为方便，取含3个节点的网络进行仿真.

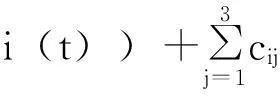
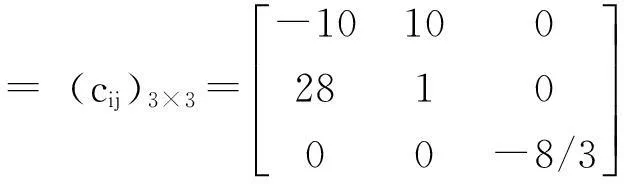
选取分数阶Lorenz系统为例，驱动系统描述为

响应系统设计为

误差系统为

其中， a、b和c为系统参数．当α=0.93, a=10, b=28, c=8/3时系统处于混沌状态． 为了方便，取含3个节点的网络进行仿真．

定理1中选取控制器

其中， A=I3； li=1； ki=1； γ=0.5； μ=0.95． 系统初始值(x1(0), x2(0), x3(0))=(1,2,-1)， 选取步长为0.01 s，所得误差曲线如图1．可见，当T>0.043 s后，系统取得同步．

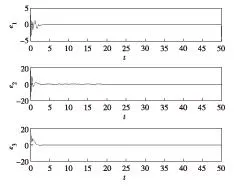
图1　定理1的系统误差曲线(N=3)Fig.1　The system error curves of theorem 1 (N=3)

定理2以下述系统为例：

其误差系统为

Δf(x1)+u1(t)

Δf2(y2)-Δf2(x2)+u2(t)

Δf3(y3)-Δf3(x3)+u3(t)

其中，Δf1=-0.1sin(4t)x1;Δf2=0.1sin(3t)x2;

Δf3=0.15sin(t)x3;

A=I3; li=1; ki=1; γ=0.5; μ=0.95. 系统初始值(x1(0), x2(0), x3(0))=(1,1,-1)， 选取步长为0.01 s，误差曲线如图2．可见，当T>0.046 s后，系统取得同步．

图2　定理2的系统误差曲线(N=3)Fig.2　The system error curves of theorem 2 (N=3)

增加结点的数量，当N=6时，系统误差曲线如图3．可见，当T>0.056 s以后，系统取得同步，表明随着结点的增加，要求系统取得同步所需时间更长．

以下考虑系统有不同结点情形，以N=3为例，单个结点为分数阶Liu系统：

Dαy1=-y1-y22

Dαy2=2.5y2-4y1y3

Dαy3=-5y3+4y1y2

网络节点为分数阶Chen系统：

Dαx1=35(x2-x1)

Dαx2=-7x1-x1x2+28x2

Dαx3=-3x3+x1x2

图3　N=6时的系统误差曲线Fig.3　The system error curves with N=6

图4　不同结点系统的误差曲线(N=3)Fig.4　The error curves of systems with different nodes (N=3)

图5　选取不同Lyapunov函数时的误差曲线Fig.5　The error curves for different Lyapunov functions

结语

基于Lyapunov稳定性理论和分数阶微积分的相关理论，研究一类分数阶复杂网络系统的有限时间混沌同步问题，给出控制器的设计，并估计系统取得同步所需的时间，使系统能够在有限时间内实现快速同步．

引文：毛北行，王战伟. 一类分数阶复杂网络系统的有限时间同步控制[J]. 深圳大学学报理工版，2016，33(1)：96-101.

参考文献/ References：

[1] 余明哲，张友安. 一类不确定分数阶混沌系统的滑模自适应同步[J]. 北京航空航天大学学报，2014，40(9)：1276-1280.

Yu Mingzhe，Zhang You’an. Sliding mode adaptive synchronization for a class of fractional-order chaotic systems with uncertainties[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(9)：1276-1280.(in Chinese)

[2] 严胜利，张昭晗. 一类不确定分数阶混沌系统的同步控制[J]. 系统仿真技术，2013，9(4)：366-370.

Yan Shengli, Zhang Zhaohan. Synchronization control of a class of uncertain fractional-order chaotic systems[J]. System Simulation Technology, 2013, 9(4)：366-370.(in Chinese)

[3] 潘光，魏静. 一种分数阶混沌系统同步的只适应滑模控制器设计[J]. 物理学报，2015，64(4)：5051-5057.

Pan Guang, Wei Jing. Design of an adaptive sliding mode controller for synchronization of fractional-order chaotic systems[J]. Acta Physica Sinica, 2015, 64(4)：5051-5057.(in Chinese)

[4] 徐瑞萍，高存臣. 基于线性控制的一类金融系统的混沌同步[J]. 控制工程，2014，21(1)：18-22.

Xu Ruiping, Gao Cunchen. Chaos synchronization of a financial systems based on linear control[J]. Control Engineering of China, 2014, 21(1)：18-22.(in Chinese)

[5] 张云雷，吴超然. 基于反馈控制的分数阶时滞神经网络的同步[J]. 重庆工商大学学报自然科学版，2014，31(12)：49-53.

Zhang Yunlei, Wu Chaoran. Synchronization of fractional-order neural network with delay based on feedback control[J]. Journal of Chongqing Technology and Business University Natural Science Edition, 2014, 31(12): 49-53.(in Chinese)

[6] 辛道义，刘允刚. 非线性系统有限时间稳定性分析与控制设计[J]. 山东大学学报工学版，2011，41(2)：119-125.

Xin Daoyi, Liu Yungang. Analysis of finite-time stability and design of control of nonlinear systems[J]. Journal of Shandong University Engineering Science, 2011, 41(2): 119-125.(in Chinese)

[7] 杨仁明，王玉振. 一类非线性时滞系统的有限时间稳定性[J]. 山东大学学报工学版，2012，42(2)：36-43.

Yang Renming, Wang Yuzhen. The finite-time stability of a class of time-delay systems[J]. Journal of Shandong University Engineering Edition, 2012, 42(2)：36-43.(in Chinese)

[8] Mei Jun, Jiang Minghui, Wang Jun. Finite-time structure identification and synchronization of drive-response systems with uncertain parameter[J]. Communications in Nonlinear Science and Numerical Simulation, 2013, 18(4): 999-1015.

[9] 毛北行，李巧利. Lurie混沌系统的有限时间同步问题[J]. 四川师范大学学报自然科学版，2014，37(4)：497-500.

Mao Beixing, Li Qiaoli The finite-time synchronization of Lurie chaos systems[J]. Journal of Sichuan Normal University Natural Science, 2014, 37(4): 497-500.(in Chinese)

[10] Mohammad P A. Robust finite-time stabilization of fractional-order chaotic systems based on fractional Lyapunov stability theory[J]. Journal of Computation and Nonlinear Dynamics, 2012, 7(2): 021010.

【中文责编：方圆；英文责编：木南】

Finite-time synchronization control of a class of

fractional-order complex network systems

Mao Beixing†and Wang Zhanwei

Department of Mathematics and Physics, Zhengzhou Institute of Aeronautical Industry Management,

Zhengzhou 450015, Henan Province, P.R.China

Abstract：Based on the Lyapunov stability theory and fractional order system theory, we investigate the finite-time chaos synchronization problem of a class of fractional order complex network systems, propose a control law and the sufficient conditions for the synchronization of systems, and estimate the time for the synchronization of systems. It is shown that the fractional order complex network systems are finite-time synchronized under a certain condition. Numerical simulations are performed to verify the effectiveness of the proposed method.

Key words：fractional order systems; finite-time; chaos synchronization; complex network; error system; control

作者简介：毛北行 (1976—)，男，郑州航空工业管理学院副教授. 研究方向：复杂网络与混沌同步. E-mail: bxmao329@163.com

基金项目：国家自然科学基金资助项目(11404291)；河南省高等学校重点科研资助项目(15B110011)

中图分类号：O 482.4

文献标志码：A

doi：10.3724/SP.J.1249.2016.01096