基于加权滑动平均的磁盘使用率预测模型

张宗华，张海全, 李师航，牛新征

1)南京南瑞集团公司流程与信息管理中心，江苏南京 211106；2)西南财经大学经济信息工程学院，四川成都 611130；

3)电子科技大学计算机科学与工程学院，四川成都 611731



基于加权滑动平均的磁盘使用率预测模型

张宗华1，张海全1, 李师航2，牛新征3

1)南京南瑞集团公司流程与信息管理中心，江苏南京 211106；2)西南财经大学经济信息工程学院，四川成都 611130；

3)电子科技大学计算机科学与工程学院，四川成都 611731

摘要：为能提前做好扩容准备，提出一种改进的加权滑动平均(weighted moving average, WMA)模型，用以预测未来短期内磁盘的使用率. 针对磁盘使用率序列变化较为平缓、要求滞后较小的特性，采用自相关和偏自相关系数法对模型定阶，处理数据后，在不影响精度的前提下计算最小滞后值，并使用结合了拉依达准则的权重转移法来均衡权重，用多新息递推最小二乘法对参数进行更精确的估计，以提高预测的准确性. 通过Matlab仿真实验可知，该算法预测误差小，滞后性弱，与原始WMA模型相比，具有更好的预测效果.

关键词：计算技术；加权滑动平均模型；磁盘使用率；自相关和偏自相关系数法；拉依达准则；权重转移；多新息递推最小二乘法

Disk usage prediction based on an improved

weighted moving average method

Zhang Zonghua1†, Zhang Haiquan1, Li Shihang2, and Niu Xinzheng3

磁盘使用率的预测主要用于资源管理、故障管理、实时监控以及对异常情况进行警报，防止磁盘写满造成数据丢失等问题. 目前有关磁盘使用率预测的研究不多.Murray等[1]提出了一种融合线性和指数回归模型、自回归积分滑动平均模型及贝叶斯结构时间序列模型的算法，而在磁盘使用率短期预测方面目前尚欠有效算法.

短期预测要求精度较高，延迟较小，比较适合用时间序列模型[2]进行预测. 常见的时间序列预测模型包括用来对各种自然现象进行预测的自回归(auto regressive, AR)模型、通过一组时间序列逐次移动完成计算的滑动平均(moving average, MA)模型、由自回归模型和滑动平均模型迭加形成的自回归滑动平均(auto regressive moving average, ARMA)模型及经过差分处理后转化为ARMA并与之形式类似的自回归积分滑动平均模型(auto regressive integrated moving average, ARIMA). 磁盘使用率数据没有明显趋势性，变化较平稳，而在时间序列模型中，MA模型最适合处理平稳数据，且运行效率高，符合预测和警告的即时性要求，已在诸如股票交易、降雨风速和金融时间序列等方面有大量应用[3-4]，取得了较好的预测效果. MA模型基本类型可以分为简单滑动平均(simple moving average, SMA)模型和加权滑动平均(weighting moving average, WMA)模型[5]，SMA模型是用过去若干个时间点的平均值来预测当前的时间值，但是忽略了各个时间点对当前时间点的影响并不相同的问题，而实际上离当前时间更接近的时间点通常都会对预测时间点造成更大的影响. 而WMA模型则可以在不同的时间点上分配不同的权值，让那些对预测点影响更大的时间点拥有更大的权值，以减小过去较远时间点造成的干扰.

针对以上问题，本研究选择WMA模型对磁盘使用率进行预测，对传统WMA模型进行改进，以保证其在处理磁盘使用率数据时能有更好的预测效果. 在保证精度的前提下减小滞后值[6]，并在传统WMA模型上加入权重转移[7]，用来防止采集数据时的意外误差对预测造成的影响，并结合拉依达准则[8]，将出现异常的时间点的权重值转移到其他正常的时间点上，而不是像传统的权重转移法只对丢失值进行处理，最后通过多新息递推最小二乘算法[9]求出参数估计，得到更好的拟合效果. 经实验验证，与传统的SMA和WMA比较，本算法可有效减小误差，对磁盘使用率序列滞后现象的修补效果也十分良好.

1磁盘使用率预测模型

WMA模型属于MA模型的一种. MA模型是一种常见的标准线性模型. 设εt是白噪声序列， i为序列指标. 若时间序列yt满足

yt=εt-α1εt-1-α2εt-2-…-αqεt-q

(1)

则称yt为q阶滑动平均序列，简称MA(q)序列[10]. 式(1)中， αi是滑动平均因子(moving average coefficients, MACs).

本研究将WMA模型做出适当改进，使其更符合磁盘使用率预测的要求，具体建模步骤如下：

1) 通过磁盘使用率数据的自相关和偏自相关系数来对模型定阶[11]，确定的阶数即为后面需要计算的参数个数；

2) 对时间序列进行平稳性检验、消除奇异值和数据平滑[12]等处理，避免一些数据波动造成的影响，减小随机误差，使后面要进行的参数估计更加精确；

3) 通过均方误差公式计算得到最小误差的最小滞后值，将得到的滞后值作为返回值参与计算，可在相同计算精度下减小滞后值；

4) 使用结合了拉依达准则的权重转移法给各个时间点赋予权值，保证赋权的有效性；

5) 用多新息递推最小二乘算法进行模型参数估计[13-21]，将其值代替MA模型表达式中的参数.

至此模型建立完毕.依此模型，用采集得到的真实磁盘使用率数据进行Matlab仿真，验证算法的有效性.

1.1模型定阶

WMA模型的阶数通过对应MA模型的阶数来确定. 本研究使用自相关和偏相关系数法来确定模型阶数，首先对序列的自相关系数(auto correlation function, ACF)和偏自相关系数(partial auto correlation function, PACF)进行计算，然后通过对其拖尾性和截尾性的判断来确定模型的类型及阶数. 拖尾性指这2个系数随延迟k无限增长以负指数的速度趋向于0；截尾性指它们在k大于模型阶数后，其值变为0. 具体判断规则如表1. 其中，AR(p)和MA(q)分别表示p阶AR模型与q阶MA模型.

表1　模型及阶数判断标准

设x1,x2,…,xT是平稳的磁盘使用率时间序列XT的一个样本，则其自协方差系数定义为

(2)

(3)

样本偏自相关系数定义为

(4)

其中，

(5)

由Bartlett公式，对于q>0， 自相关系数满足正态分布

(6)

当样本容量充分大时，有

(7)

(8)

对于每个q>0, 检查从第q+1个开始的ACF落入如式(9)范围中的比例是否占总数的68.3%或95.5%左右.

(9)

如果在首阶数q0之前，ACF都明显不为0，而在q=q0时，ACF中满足式(9)的个数达到上述比例，则可判断ACF序列在q0处截尾，即序列Xt为MA(q0)序列. 计算实际磁盘使用率序列得到的结果如表2.

表2　自相关系数与偏自相关系数

因表2数据满足式(9)条件，则可判断磁盘使用率数据在k=1处截尾，即q0=1， 故此时间序列是符合MA(1)模型的，即磁盘使用率时间序列是符合1阶WMA模型的.

1.2数据处理

对磁盘使用率的数据处理包括平稳性检验、消除奇异值和平滑数据等方面. 表2自相关系数序列同时可以用作平稳性检验的标准. 当自相关系数序列快速衰减至0，则说明此时间序列是平稳序列.由表2可见，磁盘使用率序列是平稳序列.

(10)

(11)

若序列中的值满足式(12)条件则予以剔除，有

(12)

将与样本均值的差值超过3倍标准差的数值确定为异常值，并将其用样本均值代替.

数据平滑的方法有滑动窗口平均法、滑动窗口拟合多项式平滑法、分量回归平滑法、小波变换法和傅里叶变换法等. 磁盘使用率数据本身变化较为平缓，不需要过多的平滑处理，故为了节省运算成本，并取得较好的平滑效果，本研究选取二次滑动窗口平均法来进行数据平滑，设定窗口大小为5个时间点，原理如下：

(13)

其中， y(i)为第i个时间点的值； yy(j)为第j个时间点经平滑处理后的值.

对经过1次平滑后的序列yy(j)用式(13)的方式进行第2次平滑处理，经2次处理后数据的随机误差减小. 用平滑后的序列进行预测，可以保证数据精度，提高预测准确性.

1.3滞后性的改进

由于滑动平均因子的对称性，WMA模型预测有大约(n+1)/2个时间点的滞后，而进行短期的磁盘使用率预测时要求较小的滞后. 故在通过式(14)计算得到的一系列滞后值中，选取造成误差最小的.

(14)

其中，

(15)

其中， α是滑动平均因子. 根据原始输入序列，可以得到输出序列的滞后值为

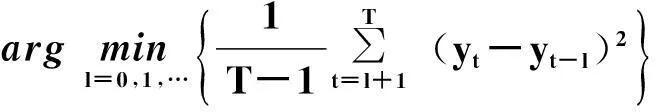
(16)

式(16)使用了均方误差作为衡量标准，用于计算每个滞后值造成的误差，其中造成最小误差的滞后值就作为模型的因子来计算输出，可有效减小磁盘使用率预测模型的滞后性问题.

1.4改进的权重转移

结合拉依达准则法与权重转移法，将不在假设检验范围内的异常点的权重交移给当前预测中权重最大的点，针对磁盘使用率数据中出现的异常波动，加强优化效果.

传统的权重转移是基于WMA模型提出的，将模型中已分配权重但实际值不存在的时间点的权重，重新分配给对当前预测目标点影响最大的时间点. 原始的权重转移法只处理拥有权重但实际值为零的点，即处理丢失值，但对其他异常数据并不敏感，只在极少数情况下才能起到作用，用途受到极大限制. 现将其与达依拉准则结合，即在对每个当前值进行预测时，将每个赋有权重的点依次排成序列，并对此权重序列进行拉依达准则的判断，对于不满足拉依达准则的点，将其权重值重新分配给对当前预测目标点影响最大的点.

如现有磁盘使用率数据中的5个时间点y1、y2、y3、y4和y5分别对应权重值w1、w2、w3、w4和w5， 用以预测下一时间点y6， 根据加权滑动平均公式有

y6=y1w1+y2w2+y3w3+y4w4+y5w5

(17)

若通过计算发现y2满足式(12)，根据上述规则，将要除去的点的权值赋给对当前目标点影响最大的点，而此例中y5距离目标点y6最近，影响最大，故将y2的权值w2转移到y5上，即此刻预测值满足

y6=y1w1+y3w3+y4w4+y5(w5+w2)

(18)

通过改进的权重转移，可有效避免因磁盘使用率数据的异常波动而造成的预测误差.

1.5参数估计

若将磁盘使用率预测模型描述为

y(t)=D(z)v(t)

D(z)=1+d1z-1+d2z-2+…+dvz-v

(19)

其中， y(t)为系统输出观测序列； v为白噪声； z为单位后移算子； di为待计算参数.且有

z-1v(t)=v(t-1)

(20)

设整数p为新息长度(innovation length)， Y(t)为堆积输出向量， V(t)为堆积误差向量， Γ为信息矩阵， θ为对参数di的估计基于最小二乘优化原理[21]，有多新息递推最小二乘法(multiple innovation recursive least squares，MILS)为

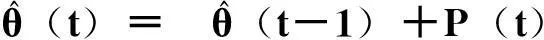
(21)

(22)

(23)

[φ(t),φ(t-1),…,φ(t-p+1)]T

(24)

具体步骤的伪代码如下：

Pseudocode of MILS

set p0=106, P(0)=p0I,θ(0)=1n/p0;

for t=1 to v do

constuct P(t), V(p,t);

for t=1 to n do

choose a new p;

end

end

该算法执行了递阶计算过程，在设置初值后，用式(24)构造Γ(p,t)， 用式(22)构造P(t)， 用式(23)计算V(p,t)， 用式(21)刷新估计值. 经以上计算逐次刷新对di的估计值θ， 则可完成对磁盘使用率模型的所有参数估计.

通过第1节的各步骤，参数估计完毕，模型建立完成.

2实验结果及分析

为验证本算法的有效性，现对不同编号的10个磁盘进行一段时间的使用率记录，磁盘类型为jfs2，操作系统为aix. 本研究采取的记录方式为每隔10 min对磁盘进行1次采样，每个磁盘的采样点保证在300个以上. 得到每个磁盘使用率的时间序列，用于进行Matlab仿真实验.

将传统的WMA和SMA与本研究算法对比，用平均绝对误差(mean absolute error, MAE)作为评判标准. 平均绝对误差是每个时间点上预测值与真实值之差绝对值的平均，相比平均误差，能真实反映预测误差，使结果具有良好的参考价值. MAE的计算公式为

(25)

其中， x(i)是原始时间序列; y(i)是预测时间序列.

各算法的预测结果对比如表3.

表3　算法平均绝对误差对比

由表3可以看到，本研究算法相对于原始的WMA，平均绝对误差减小了24%～73%，在磁盘使用率序列上取得了良好的效果.

本研究用Matlab实现仿真[22]，对10组磁盘使用率数据进行处理和预测，部分实验结果如图1.

图1　自相关系数Fig.1　Autocorrelation coefficients

图1中将表2的自相关系数用散点图画出，并将判断是否落在范围内的标准差用与x轴平行的两条实线标记，可以更明确地看到Lag=1时的点落在实线外，而后面的值都迅速衰减到0左右，并在x轴附近进行无规则的上下波动，根据以上情况可判断该时间序列符合MA(1)模型.

采集到的原始时间序列如图2.

图2　采样后的原始时间序列Fig.2　Original time series of sampling

图2是10组磁盘使用率序列中的一组，可以看到磁盘使用率时间序列极其平缓，甚至会在几个连续时间点里数值保持不变，但在图2中很明显有2个点的数值比其他点高出很多，所以需要处理数据，以避免一些非算法精度问题造成的影响. 图3为处理后的时间序列.

图3　经数据处理后的时间序列Fig.3　Time series after processing

由图3可以清晰看到磁盘使用率序列经过600多次采样，变化范围都在94.8～95.0，明显高于其他数据的值被判断为异常值并予以剔除. 处理过后的序列消除了异常情况和随机误差的干扰，可以进行预测，其预测结果如图4.

图4　预测结果拟合图Fig.4　Fitting curve of prediction result

图4给出了本研究改进的WMA模型的预测序列与原始时间序列的拟合图，由于采样点太多，此图只能粗略地看到预测效果，所以截取了其中一小部分数据并放大，与原始SMA和WMA算法对比.

图5截取了序列中变化较频繁的一段，可以更好地看出拟合效果.由图5可见，改进后的WMA拟合效果优于SMA和WMA，预测误差明显减小，能快速感知数据变化，且滞后也显著减小，较好地解决了磁盘使用率预测中对高预测精度和较小滞后的需求.

图5　改进算法与SMA和WMA的对比图Fig.5　(Color online) Comparison diagram of prodiction by the proposed algorithm, SMA and WMA

结语

本研究提出了一种对WMA模型的改进算法，对真实磁盘进行使用率数据采样，通过Matlab仿真验证了算法的有效性. 实验结果显示本算法优化效果良好，在减小预测误差和滞后方面效果显著.仿真过程中发现，若数据出现连续的上下剧烈波动，则预测效果变差，即本算法对较尖锐的波峰波谷预测能力不强，虽然这种数据出现剧烈波动的情况在磁盘使用率数据中极为罕见，但也值得考虑并做出改进.

引文：张宗华，张海全, 李师航，等. 基于加权滑动平均的磁盘使用率预测模型[J]. 深圳大学学报理工版，2016，33(1)：72-79.

参考文献/ References：

[1] Murray S,Amaan M,Christoph A, et al. Projecting disk usage based on historical trends in cloud environment[C]// The 3rd ACM Workshop on Scientific Cloud Computing. Delft, Netherlands: Association for Computing Machinery, 2012.

[2] Husna S H, Cui Lishan, Herny R H. Time series analysis of Web server logs for an online newspaper[C]// Proceedings of the 7th International Conference on Ubiquitous Information Management and Communication. Kota Kinabalu, Malaysia: Association for Computing Machinery, 2013.

[3] Ahmad A S A,El-Shafie A,Naseri M, et al. Rainfall data analyzing using moving average (MA) model and wavelet multi-resolution intelligent model for noise evaluation to improve the forecasting accuracy[J]. Neural Computing and Applications, 2014, 25(7): 1853-1861.

[4] Raudys A. Optimal negative weight moving average for stock price series smoothing[C]// Conference on Computational Intelligence for Financial Engineering. London: Institute of Electrical and Electronics Engineers, 2014.

[5] Hansun Seng. A new approach of moving average method in time series analysis[C]// International Conference on New Media Studies.Tangerang,Indonesia: IEEE Computer Society, 2013.

[6] Adrian L, Gao Junbin, Zheng Lihong. Optimizing the moving average[C]//World Congress on Computational Intelligence. Brisbane,Australia: Institute of Electrical and Electronics Engineers Inc, 2012.

[7] 杨慧,许福栗. 基于权重转移的加权滑动平均模型改进[J].计算机工程与应用, 2014, 50(14):156-159.

Yang Hui, Xu Fuli. Improvement of weighted moving average model based on transferring weights[J]. Computer Engineering and Applications, 2014, 50(14):156-159.(in Chinese)

[8] Zhang Liang, Qin Yongyuan, Zhang Jinliang.Study of polynomial curve fitting algorithm for outlier elimination[C]// International Conference on Computer Science and Service System.Nanjing, China: IEEE Computer Society, 2011.

[9] 周易,丁峰. 滑动平均模型的最小二乘辨识方法比较研究[J].科学技术与工程, 2007, 18(7): 4570-4575.

Zhou Yi, Ding Feng. Comparison of least squares identification for moving average models[J]. Science Technology and Engineering, 2007, 18(7): 4570-4575.(in Chinese)

[10] 卜爱国,王炯. 基于MA(q)模型的动态电源管理预测策略[J].计算机应用研究,2011,28(7): 2516-2518.

Bu Aiguo, Wang Jiong. Dynamic power management predictive policy based on MA(q) model[J]. Application Research of Computers, 2011,28(7): 2516-2518.(in Chinese)

[11] 张贤达. 用自相关确定MA模型阶数的二种新方法[J].电子学报, 1994, 22(7): 103-104.

Zhang Xianda. Two new mothods for order determination of an MA model using autocorrelations[J]. Chinese Journal of Electronics, 1994, 22(7): 103-104.(in Chinese)

[12] 王达, 崔蕊.数据平滑技术综述[J]. 电脑知识与技术, 2009, 17(5)：4507-4509.

Wang Da, Cui Rui. Data smoothing technology summary[J]. Computer Knowledge and Technology, 2009, 17(5)：4507-4509.(in Chinese)

[13] 李守巨,霍军周,曹丽娟. 盾构机土压平衡系统的ARMA模型及其参数估计[J]. 煤炭学报, 2014, 39(11)：2201-2205

Li Shouju, Huo Junzhou, Cao Lijuan. Autoregressive moving average model and its parameter estimation for earth pressure balance system of shield[J]. Journal of China Coal Society, 2014, 39(11)：2201-2205.(in Chinese)

[14] 宋安超. 滑动平均模型参数估计方法的仿真比较[J]. 大众科技, 2011, 12(1)：49-51.

Song Anchao. Simulation and comparison of three methods of parametric estimation for moving average model[J]. Popular Science and Technology, 2011, 12(1)：49-51.(in Chinese)

[15] 汪海滨,龙俊波,查代奉. 分数低阶时频滑动平均模型参数估计[J]. 计算机工程与应用, 2015, 50(20)：178-182.

Wang Haibin, Long Junbo, Zha Daifeng. Modeling and parameter estimation based on FLO-TFMA[J]. Computer Engineering and Applications, 2015, 50(20),178-182.(in Chinese)

[16] 单锐,施苏桐,刘文. 基于改进共轭梯度思想的滑动平均模型参数估计优化方法[J]. 兰州理工大学学报, 2014, 40(1)：144-147.

Shan Rui, Shi Sutong, Liu Wen. The auto regression moving average model optimization method of parameter estimation based on the improved conjugate gradient thoughts[J]. Journal of Lanzhou University of Technology, 2014, 40(1)：144-147.(in Chinese)

[17] 邓自立. 滑动平均模型参数估计的Gevers-Wouters算法的指数收敛性[J]. 科学技术与工程, 2005, 20(5)：1473-1484.

Deng Zili. Exponential convergence of Gevers-Wouters algorithm for moving average model parameter estimation[J]. Science Technology and Engineering, 2005, 20(5)：1473-1484.(in Chinese)

[18] 单锐,刘雅宁,刘文. 改进的差分自回归移动平均模型的共轭梯度参数估计法[J]. 河南科技大学学报自然科学版, 2015, 36(4)：85-90.

Shan Rui, Liu Yaning, Liu Wen. Improved conjugate gradient parameter estimation for autoregressive integrated moving average model[J]. Journal of Henan University of Science and Technology Natural Science, 2015, 36(4)：85-90.(in Chinese)

[19] 高艳普,王向东,王冬青. 多变量受控自回归滑动平均系统的极大似然辨识方法[J]. 山东大学学报工学版, 2015, 45(2)：49-55.

Gao Yanpu, Wang Xiangdong, Wang Dongqing. Maximum likelihood identification method for a multivariable controlled autoregressive moving average system[J]. Journal of Shandong University Engineering Science, 2015, 45(2)：49-55.(in Chinese)

[20] 李天一,郑建荣.基于ARMAX模型的子空间辨识算法[J]. 计算机仿真, 2015, 32(1)：310-313.

Li Tianyi, Zheng Jianrong. A new subspace identification method based on ARMAX model[J]. Computer Simulation, 2015, 32(1)：310-313.(in Chinese)

[21] Ding Feng,Cheng Tongwen. Hierarchical least squares identification methods for multivariable ststems[J]. IEEE Transactions on Automatic Control，2005, 50(3): 397-402.

[22] 王国峰,王子良,王太勇,等. Matlab在时间序列分析中的应用[J]. 应用科技, 2003, 30(5):36-38.

Wang Guofeng, Wang Ziliang, Wang Taiyong, et al. Application of Matlab in time series analysis[J]. Applied Science and Technology, 2003, 30(5): 36-38.(in Chinese)

【中文责编：坪梓；英文责编：远鹏】

1) Process and Information Management Center, NARI Group Corporation, Nanjing 211106, Jiangsu Province, P.R.China

2) College of Economics and Information Engineering, Southwestern University of Finance and Economics,

Chengdu 611130,Sichuan Province, P.R.China

3) College of Computer Science and Engineering, University of Electronic Science and Technology of China,

Chengdu 611731, Sichuan Province, P.R.China

Abstract：This paper proposes an improved weighted moving average (WMA) model to predict the usage of disks in the near future. Considering the characteristics of showing gentle change in disk usage and the requirements with small lag, we firstly utilize the autocorrelation and partial autocorrelation coefficient method to determine the order of the model. After processing the series, the minimum lag can be calculated on the premise without affecting the accuracy. Additionally, weights transferring combined with the Pauta criterion is used to balance the weight. At last, we estimate the parameters by using the multiple innovation recursive least squares to improve the result of prediction. According to the simulation result by Matlab, this algorithm is proved to have less result errors and a smaller lag. It provides a better prediction effect as compared with the original WMA model.

Key words：computing technology; weighted moving average model; disk usage; autocorrelation and partial autocorrelation coefficient method; Pauta criterion; transferring weight; multiple innovation recursive least squares

作者简介：张宗华(1977—)，男，南京南瑞集团公司工程师.研究方向：电力信息化. E-mail：hangzonghua@sgepri.sgcc.com.cn

基金项目：国家自然科学基金资助项目(61300192) ；国家科技支撑计划资助项目(2013BAH33F00)；南京南瑞集团公司研究基金资助项目(SGTYHT/14-XX-194)

中图分类号：TP 301.6

文献标志码：A

doi：10.3724/SP.J.1249.2016.01072