六轮机器人逆运动学的几何诱导迭代法研究

陈广涛，吕伟新，彭俊杰

(1.上海大学 计算机工程与科学学院，上海 200444；2.中科院上海高等研究院，上海 201210)

六轮机器人逆运动学的几何诱导迭代法研究

陈广涛1，吕伟新2，彭俊杰1

(1.上海大学 计算机工程与科学学院，上海 200444；2.中科院上海高等研究院，上海 201210)

机器人控制对实时性要求高，其逆运动学的快速求解是机器人控制领域的重要问题。在传统的逆运动学求解方法中，大多采用数值迭代的方法，该方法具有一定的通用性，但是该方法同时也有迭代收敛慢或者不收敛的问题。针对数值迭代法在机器人逆运动学求解过程中遇到的运算量大、收敛速度慢、结果唯一性难保证、无法确保实时性要求的问题，提出利用机器人机构的几何特点加速迭代收敛的方法。研究机构的几何特点，找出其表达参数，仅对必要的变量进行迭代运算，其他关节变量由机构几何特点获得的解析式求得。在满足实时性要求的前提下，该方法能以较少的迭代次数达到需要的求解精度。六轮机器人是广泛研究的一种月球探测车模型，机构较为复杂。针对该具体结构的数值仿真表明，该方法快速有效。

机器人逆运动学；迭代求解；几何法诱导；摇臂式六轮探测车

0 引 言

机器人控制对实时性要求高，其逆运动学的快速求解是机器人控制领域的重要问题[1]。有些机器人无法采用解析方法求解逆运动学，采用数值解法就需要在给定时间内稳定收敛，这不但要尽量减少求解运算量，还应该排除算法中的尝试性环节。

解析法计算效率高，是保证实时性的首选，然而应用中有许多机构无法得到解析解，只能借助数值方法求解，通过选择关节变量初值，迭代逼近真实解。数值迭代法虽然能达到给定精度的运动学方程逆解，但运算量大、收敛速度与结果唯一性难保证、无法确保实时性要求[1-2]。最严重的问题是，迭代次数难以预料、计算结果具有不确定的多解性、不能确保收敛[3]。早已有人认识到减少迭代参数的意义，例如，易科[4]采用构造并求解仅含有一个关节参数的非线性方程方法，把逆解问题转化为迭代求解这个角度的问题，再进一步由解析式求得其他角度。虽然这类方法减少了计算量，但是仍然不能克服迭代是否收敛、是否存在多解的问题。

为此，文中提出一种利用机构的几何特点辅助迭代求解的方法，可避免多解问题、确保快速收敛，从而解决机器人逆运动学求解的实时性问题。由于涉及几何方法的问题通用性不显著，难以概括总结出通用法则，以一个被美国NASA等研究机构广为采用的摇臂式六轮探测车的机构模型[5-11]为例，详细介绍了该方法的基本原理，并给出其数字仿真结果。

1 摇臂式六轮车几何模型

文献[6]所给出的摇臂式六轮月球探测车结构模型如图1所示，主要由差动轴、主摇臂、副摇臂、车轮组成。其中差动轴中间的差动器使左右主摇臂相对于差动轴转动的角度互为相反数[6]。

图1 摇臂式六轮探测车结构

建立的空间坐标系如图2、3所示。

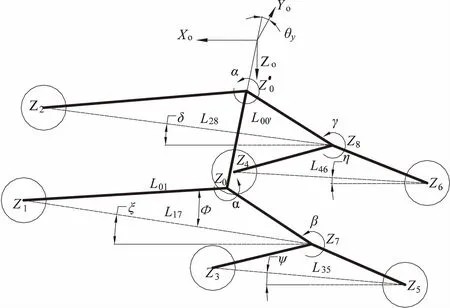
图2 摇臂式六轮探测车空间姿态

定义左右主摇臂之间的差动角度分别α和-α，左右副摇臂相对其主摇臂的转角分别为β和γ。定义差动轴坐标系OD-XDYDZD相对于空间绝对坐标系OO-XOYOZO的前向倾角为θx，侧向倾角为θy，如图3所示。可知，关节角{θx,θy,α,β,γ}确定后，各车轮的相对空间坐标随之确定，反之亦然[6]。

图3 差动轴坐标系与空间绝对坐标系相对关系

应用中感兴趣的是其6个轮心的相对高度与关节变量的关系，以便主动地适应月球的起伏地面。因此，其逆运动学求解问题就是如何从6个轮心的相对高度(即6个轮心在绝对空间坐标系ZO轴上的分量)得知关节变量{θx,θy,α,β,γ}。为此，以6个轮心等高的状态作为初始状态，并始终把最低的轮心高度设为零[7]。

2 利用几何特征引导迭代过程

2.1 几何特征分析及关系方程建立

文献[6]给出的探测车结构尺寸如图4所示。

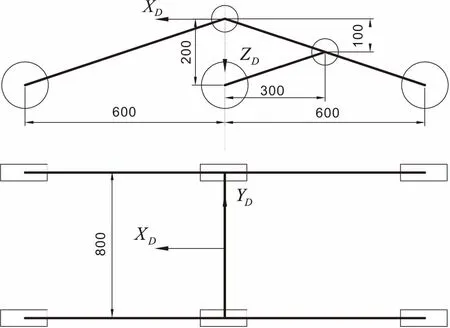
图4 摇臂式六轮探测车结构尺寸

若是以常规方式建立探测车的运动学方程，得到的是多个矩阵相乘而形成的复杂方程组，难以简化处理[6]。

利用图2所示几何关系易得到以下关系式：

(1)

(2)

(3)

(4)

(5)

(6)

(7)

Z0=Z1-L01sin(φ-ξ)cosθy

(8)

那么，容易通过中间变量表示所求关节变量：

(9)

(10)

其中，ξ0为初始状态，即6个轮心在同一高度时ξ应该取得的值。

2.2 几何特征引导迭代过程

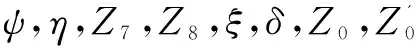
之所以选择θy作为迭代变量，首先是因为这样做可以把复杂的空间几何问题简化为平面上的问题，通过XDZD平面上的几何关系直接得到θx,α,β,γ的解析表达式。更重要的是，能够根据θy的几何意义直观地判断迭代必然收敛于一个唯一值，避免了丢失可能解和盲目探索可能解的问题。因此，选择适当的迭代变量是诱导迭代过程简化计算逆解问题的关键[12]。

利用几何关系辅助迭代求解逆运动学方法的思想是：找出机构运动过程中一个确定的几何规律，利用该规律诱导迭代过程，避开不利方向，将描述该规律的参数选作迭代变量；采用尽可能少的变量表示其他关节变量，仅对必要的变量进行迭代运算，其他间接变量或关节变量均由解析式求得[13]。

本例中θy≠0是造成计算困难的关键，而且它在引导方向上只有一个可能解，就只可能收敛于一点。由于每次更新都相当于修正了前一次假设的误差，因此能够保证足够的收敛速度。

3 数值仿真与分析

分别用常规数值求解法和文中提出的几何辅助诱导迭代的数值法对文献[6]中的机构实例进行求解，以验证算法的有效性。其常规数值求解采用Matlab的fsolve函数对6元非线性方程组进行迭代求解，细节见文献[6]。经对比发现，在所涉及表达式上，常规法求逆解的运算量明显比几何诱导法大，需要消耗更多的时间。再从迭代次数和时间消耗方面对比分析两种算法。为此选择了关节变量{θx,θy,α,β,γ}的三组不同值,通过正运动学方程求得其对应的6个轮心的高度值，然后反过来利用轮心高度作为所求逆解的已知值来求取关节变量，观察结果与事先选定的关节变量理想值的一致性[14]。为避免所用初值不同造成的影响，三组计算的迭代初值统一选为{θx,θy,α,β,γ}={0,0,0,0,0}，而几何诱导法的迭代初值也选用θy=0，两种算法计算结果所允许的误差均为ω=1×10-4。测试采用主频为2.0GHz，内存为2.0GB的WindowsXP系统MATLAB平台。实验数据如表1所示,其中求逆解计算所消耗的时间采用10 000次计算后的平均值。

表1 实验结果对比

由实验数据可以看出：几何诱导法的迭代次数远小于常规逆解法，所耗费的时间是常规逆解法的几千分之一甚至更少，特别地，当θy=0时，几何诱导法仅迭代1次即得到理想值。可见，在迭代次数与计算耗时方面，几何诱导法都明显优于常规逆解法。

4 结束语

运动方程的常规逆解法直接从机器人的运动学方程出发，采用数学工具进行多元迭代，求解非线性方程组[14]；而几何诱导法充分挖掘利用机器人机构的几何特点[12]，采用尽可能少的关节变量表示其他关节变量，仅对必要的关节变量或某一中间变量进行迭代求解[15]，在同样的运算精度要求下减少了迭代次数，单次迭代运算量也大为减少，极大地缩短了求解时间，并且避免了一般多元非线性方程组迭代方法中致命的收敛性问题，能更好地满足机器人控制的实时性和准确性要求。

[1] 陈 鹏，刘 璐，余 飞,等．一种仿人机械臂的运动学逆解的几何求解方法[J]．机器人,2012,34(2):211-216．

[2] 祖 迪，吴镇炜，谈大龙．一种冗余机器人逆运动学求解的有效方法[J]．机械工程学报,2005,41(6):71-75．

[3] 毕诸明，蔡鹤皋．六自由度操作手的逆运动学问题[J]．机器人,1994,16(2):92-97．

[4] 易 科．机器人运动学逆的数值迭代法[J]．计算技术与自动化,1992,11(2):26-30．

[5] 李所军，高海波，邓宗全．摇臂式月球车的运动学建模及悬架参数优化[J]．西安交通大学学报，2009,43(9):62-66．

[6] 周开波，王旭永，罗小桃,等．摇臂式六轮探测车空间姿态建模与求解[J]．上海交通大学学报，2013,47(7):1093-1098．

[7] 毛 宁．六轮摇臂巡视器建模仿真及试验研究[D]．长春：长春理工大学，2014．

[8] 胡 明，邓宗全，高海波,等．摇臂转向架式月球探测车越障通过性分析[J]．上海交通大学学报，2005,39(6)：928-932．

[9] 王佐伟，梁 斌，吴宏鑫．六轮月球探测车运动学建模与分析[J]．宇航学报,2003,24(5):456-462．

[10] 杨艳春，鲍劲松，金 烨．基于虚拟现实环境的六轮月球车运动性能分析[J]．上海交通大学学报,2010,44(8):1079-1083．

[11] 居鹤华，曹 亮，崔平远．基于模糊逻辑的月球车逆运动学求解方法[J]．宇航学报,2009,27(4):643-647．

[12] 刘 达，王田苗．一种解析和数值相结合的机器人逆解算法[J]．北京航空航天大学学报，2007,33(6):727-730．

[13] 蔡自兴．机器人学基础[M]．北京：机械工业出版社，2009:15-26．

[14] 宋小康，谈大龙，吴镇炜,等．全地形轮式移动机器人运动学建模与分析[J]．机械工程学报,2008,44(6):148-154．

[15] 王庆国，林建亚，路甬祥．机器人的运动学与动力学[J]．机器人,1990,12(1):58-64．

Exploration of Geometric Inducing Method in Numerical Iteration for Six-wheeled Robot Inverse Kinematics

CHEN Guang-tao1,LÜ Wei-xin2,PENG Jun-jie1

(1.School of Computer Engineering and Sciences,Shanghai University,Shanghai 200444,China;2.Shanghai Advanced Research Institute,Chinese Academy of Sciences,Shanghai 201210,China)

The automatic control of robot has a higher requirement of real-time,and it is important for automatic control to get the solution of robot inverse kinematics.In the traditional method,the solution by numerical iteration is always used,which is universal,but with the problems of slow convergence or non-convergence.Numerical iteration applied to robot inverse kinematics solution may bring the disadvantage of heavy calculation,slow convergence,the unique result not to guarantee,and good real-time performance not to determine.Therefore,a method using the geometric characteristics of robot mechanism is demonstrated to accelerate iteration convergence.It tries to find the parameters describing the geometric characteristics of mechanism studied,and need merely calculation of the iteration of key variables,while the other variables can be obtained by the analytic formula figured out by the geometric characteristics of mechanism.Applying the method can achieve the required precision by less number of iterations on the premise of meeting the real-time performance.Six-wheeled is a model of robot rover which has extensive research and complex mechanism.Numerical simulation of concrete mechanism shows the availability and high efficiency of the method.

robot inverse kinematics;iterative solution;geometric induction;six-wheeled rocker rover

2016-01-07

2016-04-19

时间：2016-11-21

国家自然科学基金资助项目(61572305)

陈广涛(1988-)，男，硕士，研究方向为机器人、机器视觉；吕伟新，博士，教授，研究方向为机器人学、自动化、机器视觉等；彭俊杰，博士，副教授，CCF会员，研究方向为云计算、嵌入式系统等。

http://www.cnki.net/kcms/detail/61.1450.TP.20161121.1633.018.html

TP301

A

1673-629X(2016)12-0041-04

10.3969/j.issn.1673-629X.2016.12.009