镜像对称的载流导线磁场方向的分析

梁 雄 赖国忠

(龙岩学院，福建 龙岩 364012)

镜像对称的载流导线磁场方向的分析

梁 雄 赖国忠

(龙岩学院，福建 龙岩 364012)

电磁场的对称性分析在大学物理教学中有着极其重要的地位，但是现有的大学物理教材很少给出如何利用稳恒磁场的对称性来分析磁感强度的方向.文章针对此问题应用毕奥-萨伐尔定律并结合矢量的分解更加便捷地分析了一对镜像对称的载流导线在中间面上任意点处的磁场方向：其方向必定垂直于该面.应用这一结论可以很容易判断出像密绕螺线管、直螺线管和圆柱形导线等这一类电流分布具有镜像对称的载流导线在其中间面上的磁感强度的方向.

毕奥-萨伐尔定律；矢量分解；镜像对称；磁场方向

大学物理教学中，电磁场的对称性分析具有很重要的地位[1].有不少文献探讨在求解电磁场问题时如何应用对称性[2-4]，但很少探讨具有高对称性的载流导线的磁场方向问题.大学物理教程中的电磁学部分通常都选取无限长直导线、无限长直螺线管以及载流螺绕环作为典型例子来说明如何应用安培环路定理求解磁感强度[5,6]，其管内的磁场大小分布容易根据载流导线的对称性分析，但对于其方向却未给出相应的分析过程.目前有文献从建立具体的坐标系，并借助于矩阵运算来分析螺绕环内部的磁场方向[7]，但求解过程比较繁琐.本文在应用毕奥-萨伐尔定律基础上，结合矢量分解更加便捷地分析得出镜像对称的载流导线在中间面上任意点的磁场方向，然后应用这一结论分析几种典型载流导线在其中间平面上所激发的磁场方向.

1 镜像对称电流元在中间平面上的磁场方向

在两线圈上对称位置取两电流元Idl(记作电流元1)和Idls(记作电流元2)，在中间平面α(简称面α)上任取一点P，则该点相对这对电流元的位矢分别记作r和rs，将电流元2和电流元1连接起来，则连线与面α相交于O点，引入两个辅助矢量d和rM：d的模等于这对电流元之间的距离，rM是P点相对于O点的位置矢量，具体参见图1.由毕奥-萨伐尔定律可得该两电流元在中间平面某点P点所产生的磁感应强度为

(1)

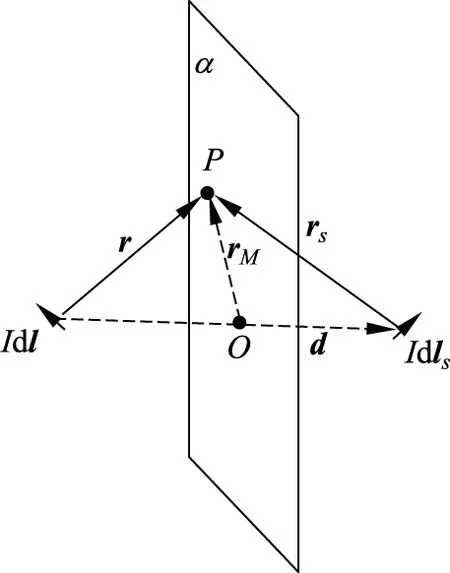
图1 对称电流元的辅助矢量分析示意图

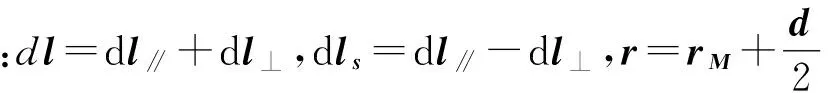
(2)

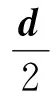
结果1：若有一对载流线圈关于某面镜像对称，则这两线圈在该面所产生的合磁场的方向一定垂直该面；

结果2：若有一对载流直导线关于某面镜像对称，则这对直导线在该面上产生的磁场方向一定垂直该面.

2 典型载流导线的磁场方向

2.1 环形密绕螺线管的内部磁场方向

如图2(a)所示，先以螺绕环的某一线圈所在平面作为中间平面α，我们来分析该线圈内某点P的磁场方向，平面α的左侧任取一线圈(记作线圈A)，则一定可以在面α右侧的对称位置上找到一线圈(记作线圈B)，按照结果1可知：这对线圈在P点的磁场一定垂直面α，因此环形螺线管的所有线圈在点P所产生的总磁场也一定与面α垂直.这就是为什么在应用安培环路定理求其磁场时要选择同心的半径为r的圆作为闭合回路.需要对学生指明一点的是：图中中间面的取法不是唯一的，所作的平面只需通过环形螺线管的环心.

同理可以分析：如图2(b)所示的直螺线管在中间面上磁场方向也必定垂直该面，对于无限长直螺线管而言任意选取一线圈所在平面都可视作中间面，因此无限长的载流直螺线管内部的磁场方向都平行于其轴线.

2.2 无限长半柱面载流导线的磁场方向

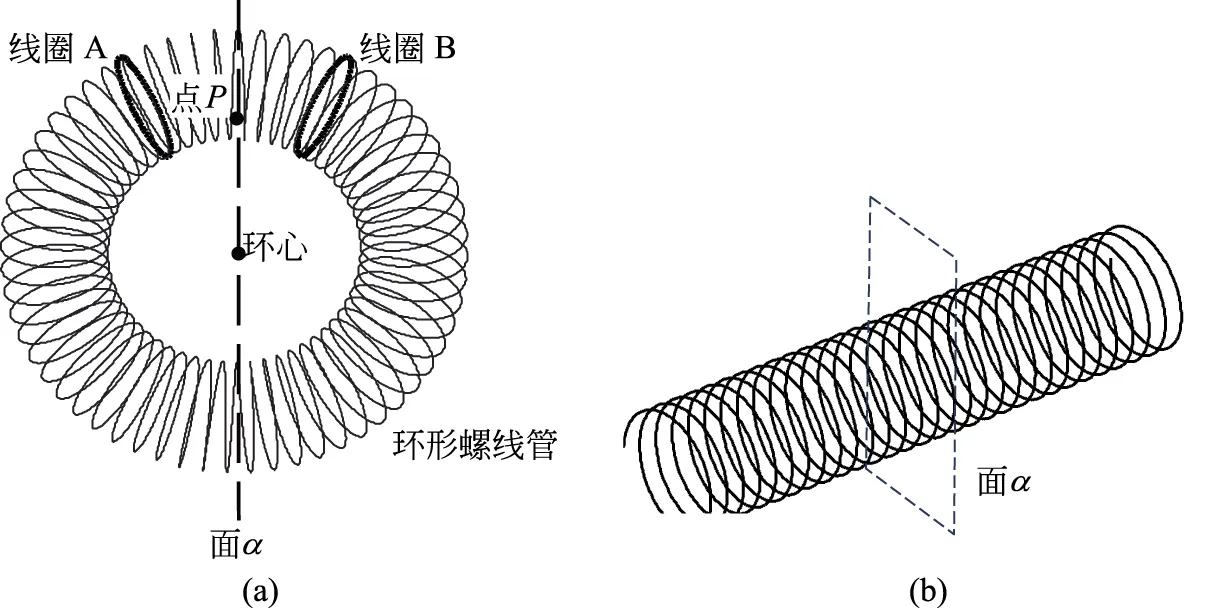
图2 螺线管

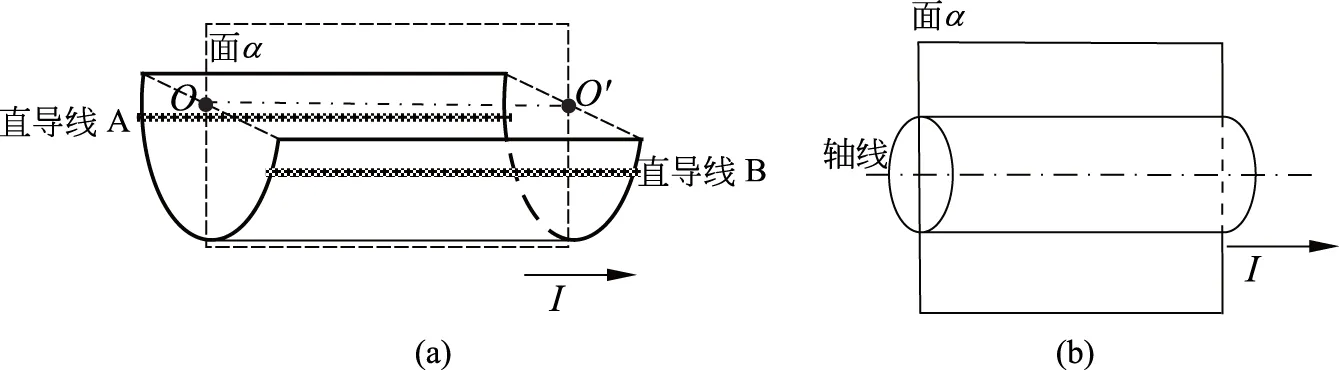
图3 半柱面形和柱体载流长直导线

文献[8]中稳恒磁场这一章的课后有一道习题：求无限长半柱面形载流导线在轴线OO′上的磁感强度，其形状如图3(a)所示.半柱面形导线可视作有许许多多的长直细导线所组成，倘若在面α的后侧取一直导线(记作直导线A)，那么在前侧对称的位置总可以找到一直导线(记作直导线B)与直导线A镜像对称，根据结果2可知，所取的这对直导线在含轴的面α上的合磁场方向垂直于面α，由此可知整个半柱面直导线在面α上所产生的磁场方向一定垂直于面α.因此求其在轴线OO′上磁感强度只需求出这些长直细导线在轴线产生的磁场在垂直于面α的分量即可.

对于图3(b)所示的柱体载流长直导线而言，可按照相同的方法来分析：这种对称电流分布在含轴的面α上的磁场方向必定垂直于面α.

3 结语

大学物理教材中应用安培环路定理求解载流导线的磁场问题，这些载流导线都是具有较强的对称性，“镜像对称分布的载流导线在中间平面上任意处的磁场方向必定垂直于该中间平面” 这结论很容易用以判断具有镜像对称的典型的载流导线的磁场方向问题.

[1] 陈熙谋,赵凯华.电磁学教学中对称性分析的积极意义[J].大学物理,2005,24(4):3-5,10.

[2] 黄亦斌,聂义友.镜象对称性在电磁学中的应用[J].大学物理,2007,26(10):24-26,30.

[3] 张淑芳,赵双义.对称性分析在电磁学中的应用[J].徐州工程学院学报：自然科学版,2008,23(4):72-76.

[4] 刘国钰.浅析对称性分析在电磁学中的应用[J].职业技术教育,2013,34(2):48-50.

[5] 梁灿彬,秦光戎,梁竹健.电磁学[M].2版.北京:高等教育出版社,2004:185-191.

[6] 马文蔚,周雨青,解希顺.物理学教程(下册)[M].2版.北京:高等教育出版社,2006:89-93.

[7] 余仕成,周金华.载流长直螺线管和螺绕环的磁场对称性分析[J].武汉工程大学学报,2010,32(5):106-107.

[8] 赵近芳,王登龙.大学物理学(下)[M].4版.北京:北京邮电大学出版社,2014:54-58,85.

■

ANALYSIS OF MAGNETIC FIELD DIRECTION OF CURRENT-CARRYING WIRES WITH MIRROR SYMMETRY

Liang Xiong Lai Guozhong

(Longyan University, Longyan, Fujian 364012)

The symmetry analysis of electromagnetic field plays an important role in the college physics teaching. But the current textbooks of university physics lack the analysis process of magnetic field direction, during solving a high symmetric static magnetic field by Ampere circulation theorem. Combining with vector decomposition, this paper presents the analysis of the magnetic field direction of current-carrying wires with mirror symmetry by the Biot-Savart law, and draws a conclusion that their magnetic field on a middle plane must be perpendicular to the plane. As applications of our conclusion, it is easy to judge the direction of magnetic field on the middle plane in this kind of mirror symmetry systems, such as the tightly wound solenoid, the straight solenoid, the cylindrical wire, and so on.

Biot-Savart law; vector decomposition; mirror symmetry; magnetic field direction

2015-11-02；

2016-01-31

福建省自然科学基金资助项目(2014J01016).

梁雄，男，讲师，主要从事大学物理教学研究，研究方向为光学薄膜技术.122746587@qq.com

梁雄，赖国忠. 镜像对称的载流导线磁场方向的分析[J]. 物理与工程，2016，26(5)：82-84.