绕月卫星软着陆最优轨道控制策略分析
崔晓琛 吴天一 张晓伟 周曰波
(镇江船艇学院,江苏 镇江 212003)

绕月卫星软着陆最优轨道控制策略分析
崔晓琛 吴天一 张晓伟 周曰波
(镇江船艇学院,江苏 镇江 212003)
对于绕月卫星的软着陆轨道问题,运用天体运动规律构建了物理模型,并利用最优化原理,把软着陆轨道控制问题转化为非线性规划问题,通过正确控制状态改变点来拟定最优控制策略.文章以嫦娥三号卫星为例,参考相关实际数据,给定相应初始条件,结合Matlab的计算结果,给出了多个相关参数随时间的变化曲线,在此基础上详细分析了卫星软着陆过程中的6个分阶段,定性讨论了在此过程中可能影响着陆精度的多种误差因素,并且通过敏感性分析给出了提升安全着落概率的方法.
软着陆;约束非线性规划;最优控制
自从人类掌握了航天技术之后,探测地外天体的首选目标就是月球,进入21世纪以来,中国的航天科技人员们提出了以发射绕月卫星为切入点的探月工程计划.绕月卫星的软着陆轨道及其控制策略关乎探月工程的成败,成为当前航天科技最为关心的话题之一.相关资料表明,由于月球上没有大气,故绕月卫星软着陆过程中主要是依靠自身携带的变推力发动机来改变其运行轨道,但并没有充分考虑合适的状态改变点.本文将绕月卫星的软着陆轨道控制问题转化为非线性规划问题,通过正确控制状态改变点,使得软着陆轨道达到最优.接着以嫦娥三号卫星为例,给出相关参数随时间的变化关系,分析软着陆过程中的6个阶段,讨论可能影响着陆精度的误差,给出提升安全着落概率的方法.
1 构建模型 拟定策略
如图1所示,绕月卫星经过地月转移轨道,在近月轨道作圆周运动,在变推力发动机的推进下,使其进入椭圆轨道,当降至近月点时开始软着陆.
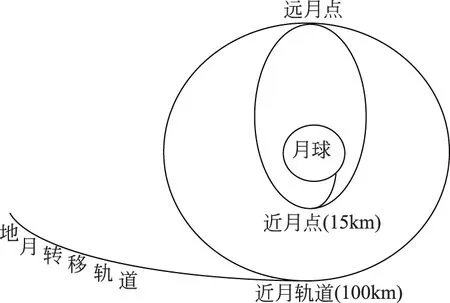
图1 绕月卫星运行轨迹示意图
考虑到降落时间较短,忽略月球自转、月球引力、日月引力摄动等因素的影响,可利用二体模型描述系统的运动,建立如图2所示的月球软着陆极坐标[1].假设着陆轨道在纵向平面内,令月心O为坐标原点,Oy轴由月心指向近月点,Ox轴指向着陆器的运动方向,其中r为着陆器的月心距;v为着陆器在矢径r方向上的速率,则有
(1)
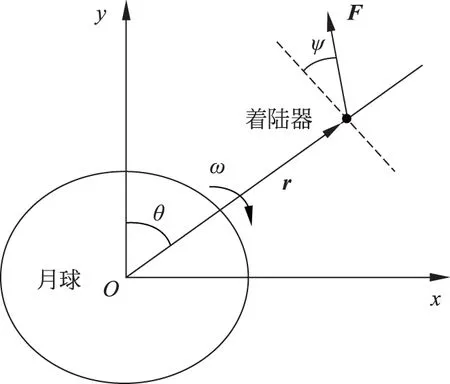
图2 月球软着陆极坐标模型
其中,θ为着陆器环绕月球表面的航程角,即矢径r与Oy轴之间的夹角;ω为着陆器绕月心的角速度,则有
(2)
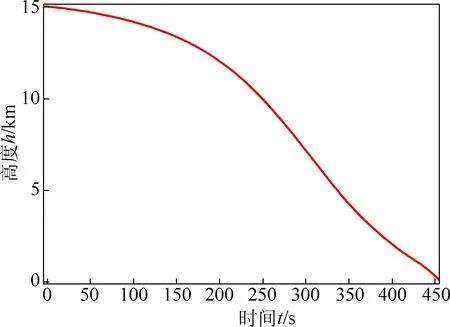
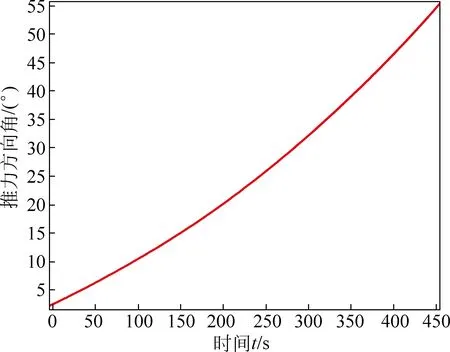
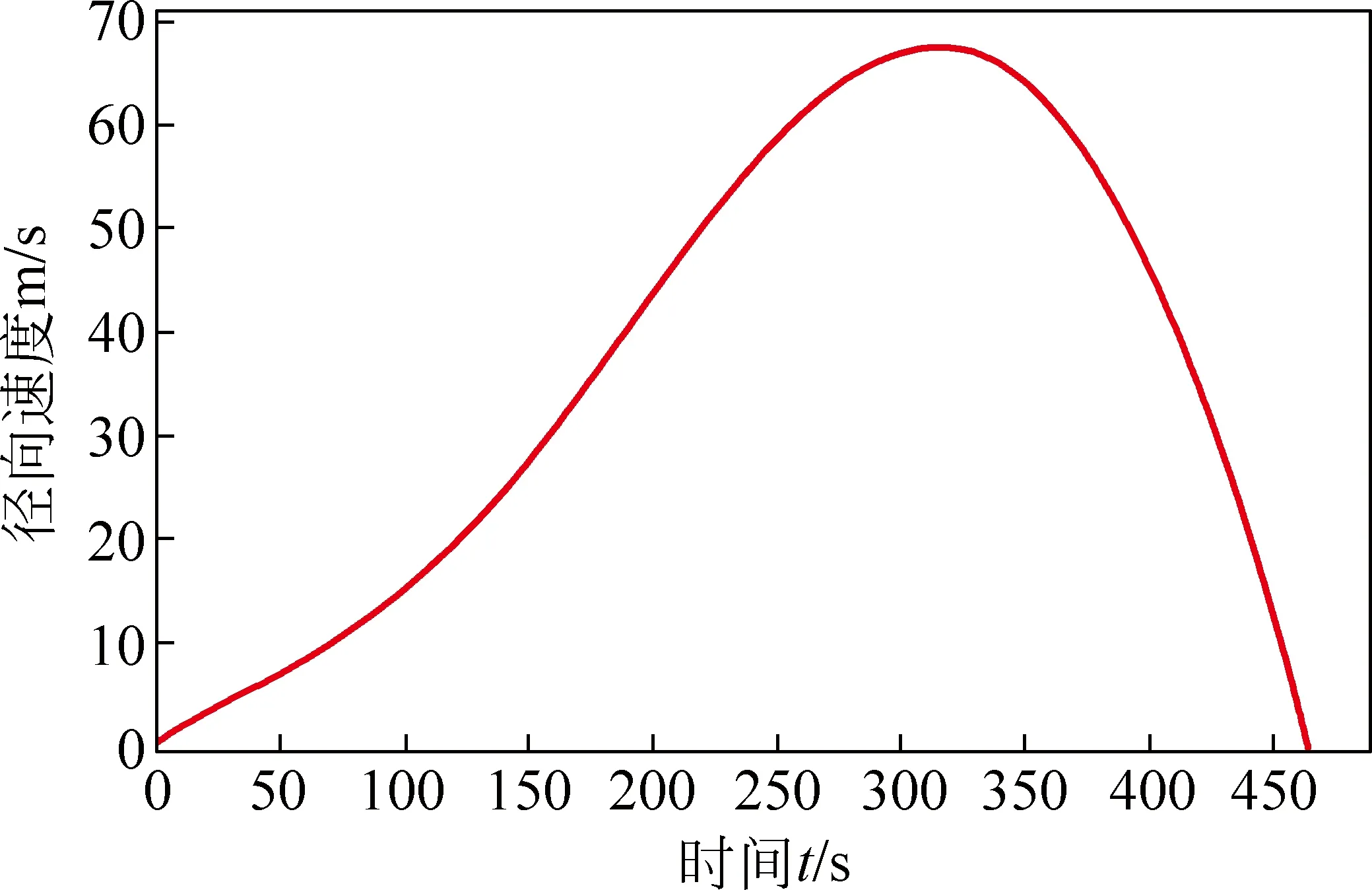
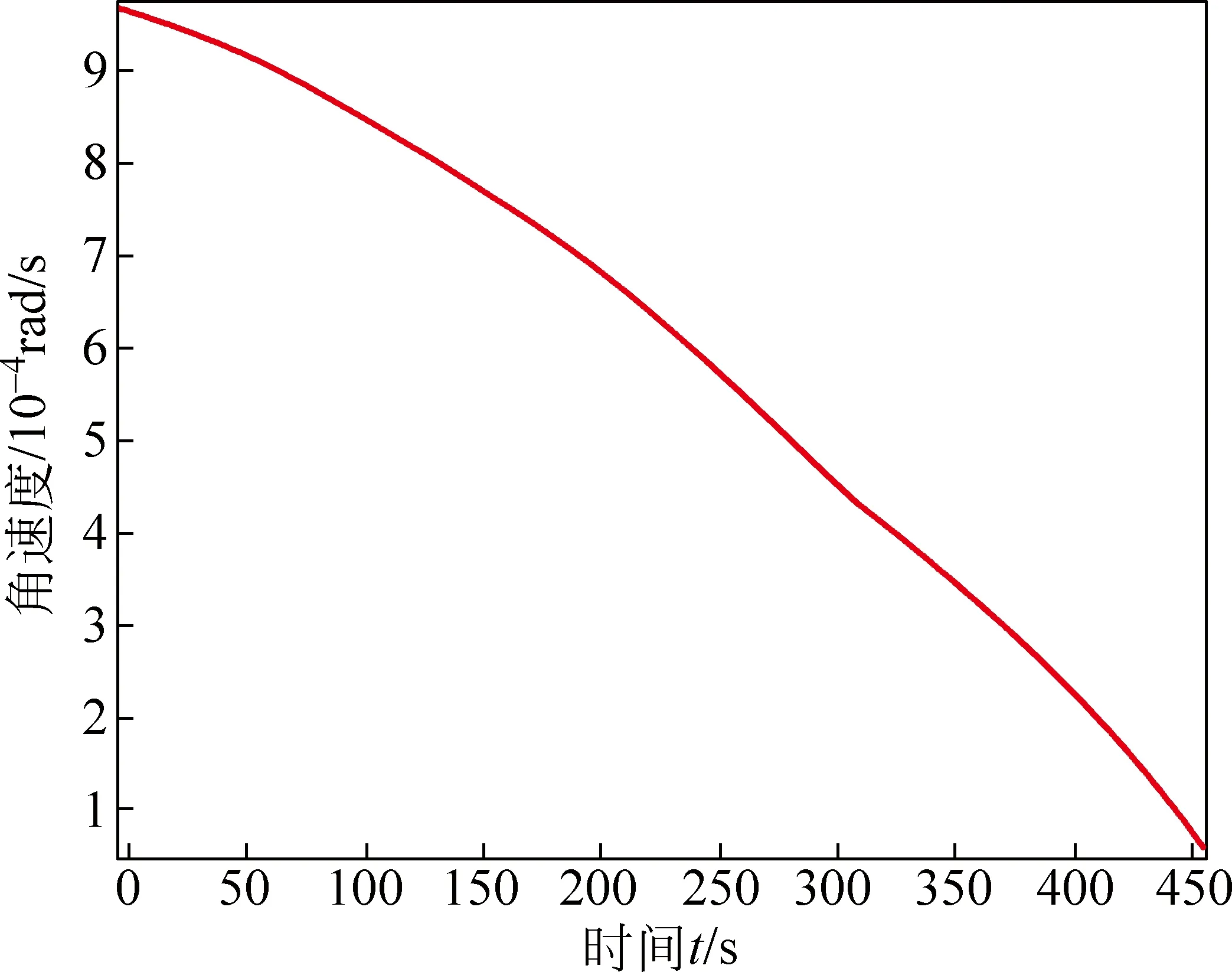
设F为制动推力器的推力,0 (3) 整理可得着陆器的质心方程组为 (6) 寻找最优控制,即使性能指标——燃料消耗量 (7) 取最小值,且满足软着陆条件 (8) 其中,t0为软着陆的初始时刻,且定义t0=0时刻的状态参数即为椭圆轨道的近月点状态参数;tf为着陆时刻,且tf未知;RM为月球半径.根据Pontryagin最大值原理[2],为了使问题简化,假设制动发动机一直以最大推力工作,即F(t)=Fmax. (9) (10) 其中, (11) 为得到各状态量随时间的变化,需增加微分方程 (12) 式(10)和(12)组成新的状态方程组,因实际计算时式(10)中的第4个方程可省略,故新的状态方程组个数不变. 目标函数变为 (13) 约束条件变为 (14) (15) 采取广义乘子法解决此有约束非线性规划问题. 定义增广拉格朗日函数 (16) 式中,λ=[λ1,λ2,…,λi]T,g(ω′)=[g1(ω′),g2(ω′),…,gi(ω′)]T. (1) 假设初始点ω′(0),乘子向量初始估计λ(1),初始罚因子σ,允许误差ε>0,参数α>1,β∈(0,1),置k=1. (2) 以ω′(k-1)为初始点,利用拟牛顿法求解无约束最优化问题minφ(ω′,λ,σ),得到解ω′(k). (17) 式中,p(k)=ω′(k+1)-ω′(k);q(k)=gk+1(ω′)-gk(ω′),gk+1(ω′)=m(ω′(k+1));可以通过有限差分得出,ω′(k)和ω′(k+1)为两个迭代点. (3) 若‖g(ω′(k))‖<ε,停止计算,得到点ω′(k);否则,继续下一步. (5) 采用下式修正乘子 置k=k+1,转步骤(2)[4]. 以嫦娥三号卫星为例,取初始条件为:r0=1753km,v0=0,θ0=0,t0=0,ω′(0)=-9.65×10-4rad/s[5],m0=2.4t;月球引力常数μ=4902.75km3/s2,月球半径RM=1738km[5];变推力发动机推力取最大值F=7500N,比冲Isp=2940m/s;控制量初值ψi=0(i=0,1,2,…,N),乘子向量初始估计λ(1)=[10,10]T,初始罚因子σ=20,允许误差ε=0.1,参数α=2,β=0.5. 利用Matlab进行计算,得到最优结果为:终端速度vf=0.05m/s,终端月心距rf=1738.013m,燃料消耗量J=1491.43kg.软着陆过程中相关参数随时间的变化曲线如图3~6所示[6]. 图3 着陆器高度随时间的变化曲线 图4 着陆器制动推力方向角随时间的变化曲线 图5 着陆器径向速度随时间的变化曲线 图6 着陆器角速度随时间的变化曲线 结合上述计算结果,软着陆过程可分为以下6个阶段: (1) 着陆准备轨道:着陆准备轨道的近月点是15km,远月点是100km.近月点位置和软着陆轨道共同决定了着陆点的位置.嫦娥三号在着陆准备轨道上绕月球运动几圈稳定后选择近月点准备着陆. (2) 主减速段:主减速段为距离月面15km降到3km.嫦娥三号沿抛物线变减速运动至3km处,速度降为57m/s. (3) 快速调整段:快速调整段为距离月面3km降至2.4km,且水平速度降为零.此阶段由于距离较短,角度不大,可看作直线运动. (4) 粗避障段:粗避障段为距离月面2.4km到100m的区间,其主要任务是要避开大的陨石坑,实现在设计着陆点上方100m处悬停,并初步确定落月地点.此阶段为变速运动,且保证悬停时嫦娥三号的重力与推力相等. (5) 精避障段:精避障段为距离月面100m到30m.要求嫦娥三号在距离月面100m的悬停处,对着陆点附近区域100m范围内拍摄图像,获得三维数字高程图.通过分析三维数字高程图,避开较大的陨石坑,确定最佳着陆地点,实现在着陆点上方30m处水平方向速度为零,在此过程中其下落速度应尽量缓慢. (6) 缓速下降阶段:缓速下降阶段的区间为距离月面30m到4m.该阶段的主要任务是控制着陆器在距离月面4m处的速度为零,即实现在距离月面4m处相对于月面静止,之后关闭发动机,使嫦娥三号自由落体到精确落月点. 1) 比冲的变化 若比冲的变化量为ΔIsp,因假定整个过程推力不变,由推力F=m′·(Isp+ΔIsp)可知,当ΔIsp>0时,其所消耗的燃料减少,那么最优控制策略不会发生改变;而当ΔIsp<0时,其所消耗的燃料就会增加,这时最优控制策略必然要发生改变,通过减少燃料的消耗以达到在规定时间内消耗的燃料最少,新的软着陆轨道控制策略必然会与原来的有所不同.而要维持比冲的数值不变,就需要对燃料的性质进行研究. 2) 探月器所受推力不通过质心 若探月器所受推力不通过质心,推力相对于质心的力矩会导致探月器发生偏转,此时推力也会在实际效用上有所降低.为了保证探月器着落在原来规定的落地点,就必须调整变推力发动机,克服探月器的偏转,即通过增加燃料耗能来满足实际需要,这时所消耗的燃料必然会发生改变,那么最优化控制策略就会发生改变.而要保证探月器所受推力始终通过质心,就需要对变推力发动机的推进方法进行研究. 3) 万有引力在水平方向上有分力 在主减速阶段,万有引力的水平分力会使得推力在水平方向上的分力发生变化,而推力在竖直方向上的分力并没有发生变化,所以推力的方向角就会变化,从而导致探月器运行轨迹的变化.在其他阶段,万有引力的水平分力会导致探月器在水平方向上发生位移,从而引起运行轨迹的变化.而要使得探月器的运行轨迹能够回到原来的轨道上来,就需要对变推力发动机的推进方法进行研究. 提高探测器软着陆的成功概率,还需进行敏感性分析.首先保证探测器尺寸不变,扩大着陆区域范围,计算相应的安全着陆概率,绘制安全着陆概率随着陆区域边长变化曲线,如图7所示;同时,保证着陆区域不变,扩大探测器尺寸,计算相应的安全着陆概率,绘制安全着陆概率随探测器尺寸变化曲线,如图8所示. 对比图7和图8的变化曲线可知,着陆区域面积大小对安全着陆概率的影响较小,探测器尺寸对安全着陆概率的影响较大.因此,为了提高行 图7 安全着陆概率随着陆区域边长的变化曲线 图8 安全着陆概率随探测器尺寸的变化曲线 星探测的成功率和生存率,在不影响科学考察的前提下,探测器的设计应尽可能地小型化. 由以上分析可知,绕月卫星软着陆过程中,着陆器的高度、制动推力方向角、径向速率和角速度都是可以人为控制的,在着陆器到达合适状态点即最佳变换时机时改变其运动状态,就可以使软着陆轨迹达到最优.在此过程中,还需考虑比冲变化、推力不通过质心、万有引力水平分力等因素造成的误差,可通过研究燃料性质和改善变推力发动机的推进方法来减小误差.由敏感性分析得知,探测器的小型化也有助于提升安全着落的概率. 备注: 此文获第二届“八一杯”军队院校大学生物理科技创新竞赛论文类二等奖. [1] 王大轶,李铁寿,马兴瑞.月球最优软着陆两点边值问题的数值解法[J].空间控制技术与应用,2000,18(3):44-55. [2] 史秀波,李泽民.用非线性方程组求解等式约束非线性规划问题的降维算法[J].经济数学,2007,24(2):208-212. [3] 周净扬,周荻.月球探测器软着陆精确建模及最优轨道设计[J].宇航学报,2007,28(6):1462,1466. [4] 陈宝林.最优化理论与算法[M].北京:清华大学出版社,2000. [5] 朱建丰,徐世杰. 基于自适应模拟退火遗传算法的月球软着陆轨道优化[J].航空学报,2007(28):806-812. [6] 赵吉松,谷良贤.基于广义乘子法的月球软着陆轨道快速优化般计[J].科技导报,2008,26(20):50-54. ■ STRATEGY ANALYSIS OF THE OPTIMAL TRAJECTORY CONTROL IN LUNAR SOFT LANDING Cui Xiaochen Wu Tianyi Zhang Xiaowei Zhou Yuebo (Zhenjiang Watercraft College, Zhenjiang, Jiangsu 212003) To deal with the soft landing orbit of sircumlunar satelite, the model is built under the motion of celestial bodies. Under the principle of optimality, the problem of soft landing trajectory control is changed into the problem of nonlinear programming. The best control strategy is made through the correct control of state variations. Taking Chang’e-3 for example, reading related real datas for reference, giving initial conditions, the changing curves of the relevent parameters as the time goes by are given out, and the 6 phases of soft landing are detailedly analysed, the errrors that may affect the landing accuracy are qualitatively discussed. After the sensitivity analysis, the method has been demonstrated to increase the probability of safety landing. lunar soft landing; constrained nonlinear optimal; optimal control 2015-11-04; 2016-02-26 崔晓琛,张晓伟,周曰波,男,2012级本科生. 吴天一,女,讲师,主要从事物理教学科研工作,研究方向为非线性动力学.wutianyiwty@126.com 崔晓琛,吴天一,张晓伟,等. 绕月卫星软着陆最优轨道控制策略分析[J]. 物理与工程,2016,26(5):89-92,96.

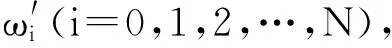
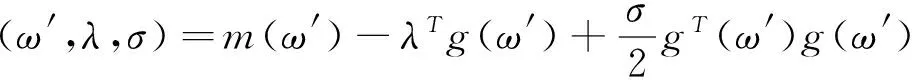
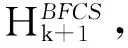
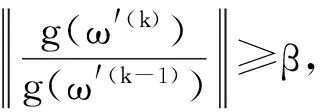
2 嫦娥三号数据分析
3 误差分析
4 安全着陆概率敏感性分析
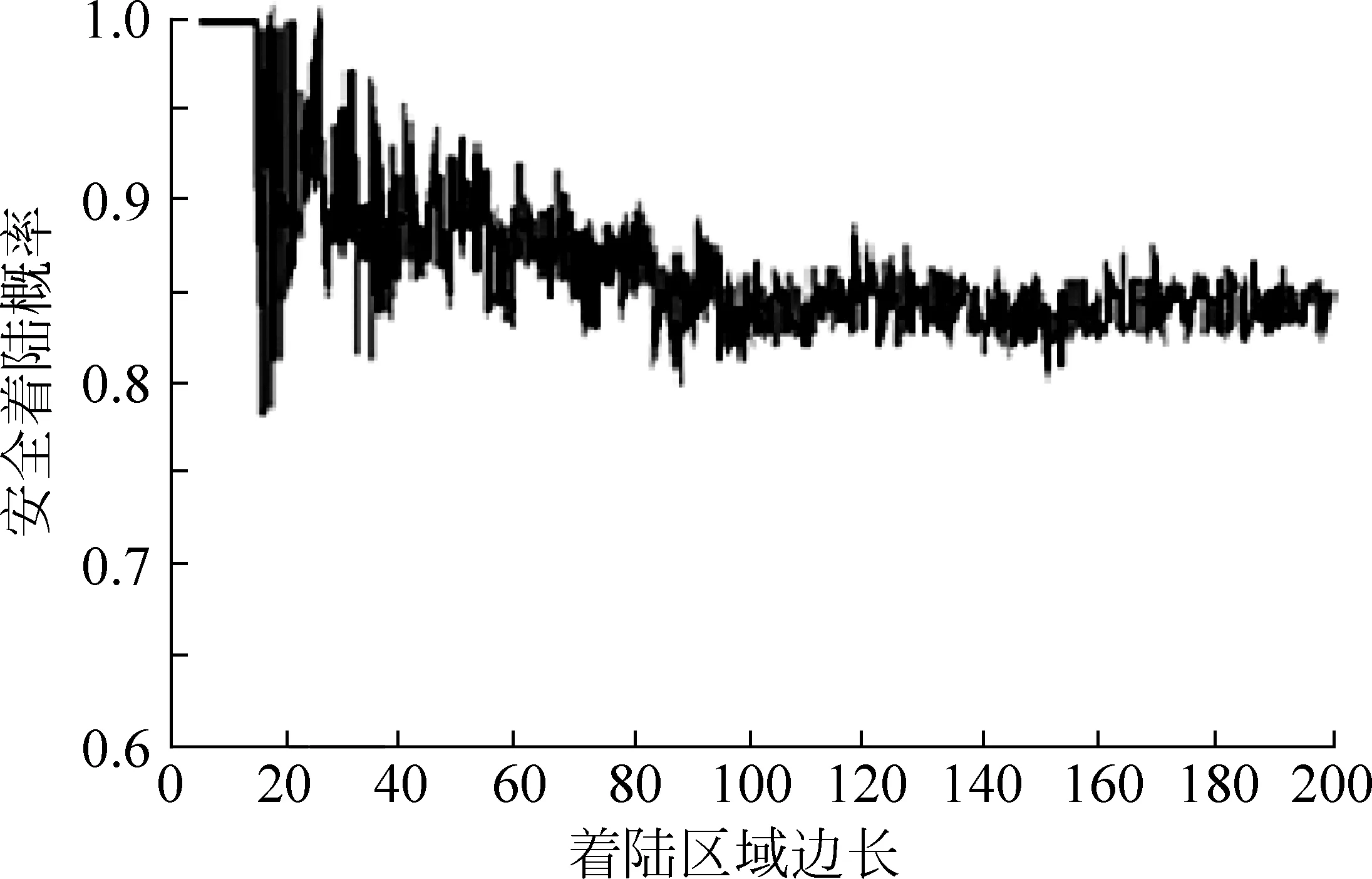
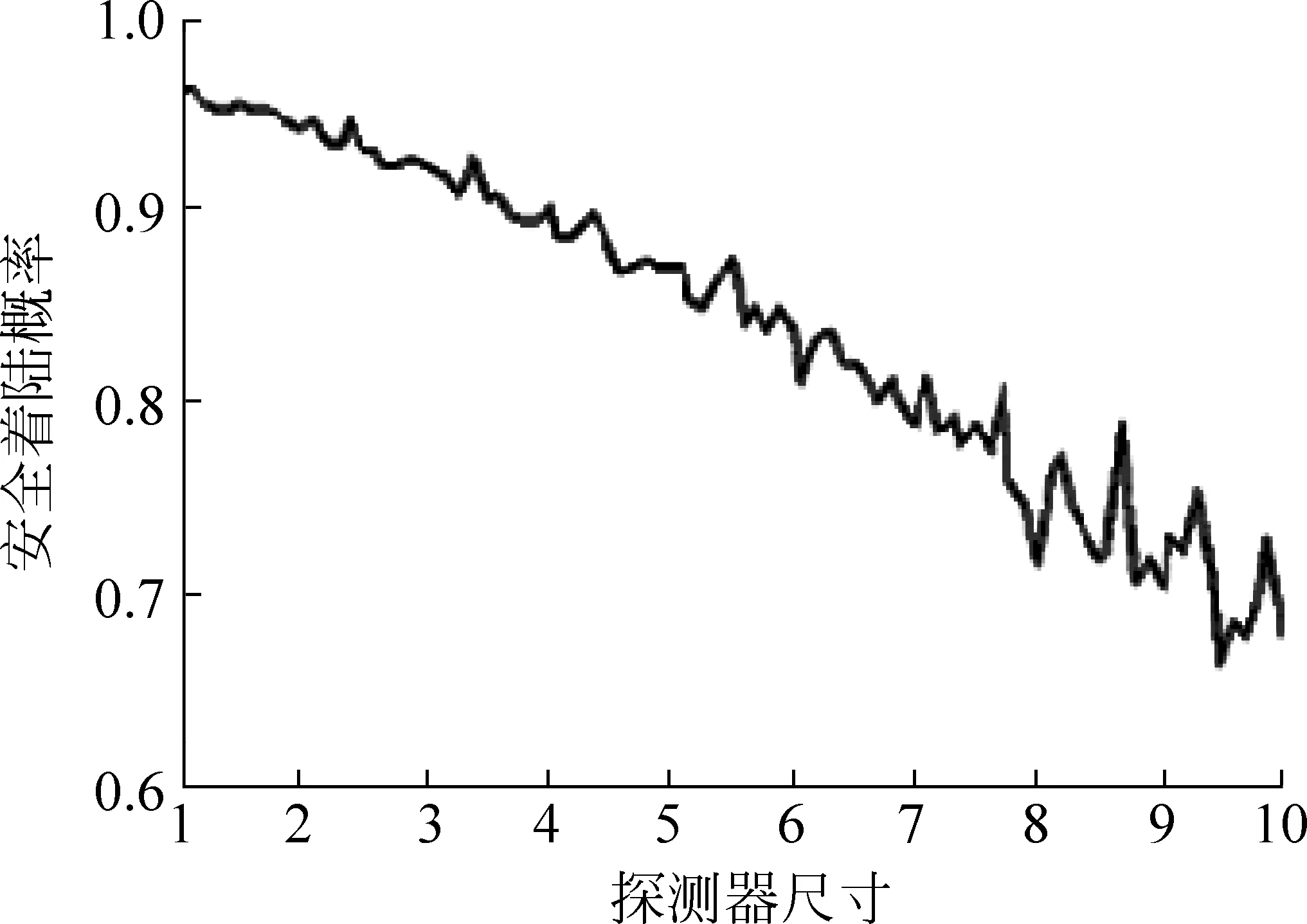
5 结语

