基于判断聚合模型对集体判断不一致的化解*
李 莉,唐 晓 嘉
(西南大学 逻辑与智能研究中心,重庆市 400715)
基于判断聚合模型对集体判断不一致的化解*
李莉,唐 晓 嘉
(西南大学 逻辑与智能研究中心,重庆市 400715)
摘要:阿罗定理证明了将完全理性个体偏好聚合为完全理性集体偏好的不可能性。这个悲观的结论对实际的集体决策过程没有帮助。如何化解聚合产生的集体意见不一致,以保证集体决策公平公正地实现集体最大利益,即实现集体决策的理性化,成为许多学科研究的热点。判断聚合模型将聚合问题放在逻辑框架之下,将集体理性聚合研究提升到一个更高的抽象水平。本文运用判断聚合模型,从分析判断困境入手,对基于前提和结论的判断聚合方法,基于多数判断集的判断聚合方法和基于权重最大的判断聚合方法进行探讨,分析了各种方法在化解集体判断不一致上的优势及局限。这些方法尽管有一定局限,但能够求得一致的集体判断集,并且逻辑形式刻画技术也使这些方法能够运用于计算机和人工智能领域中的推荐系统、多主体决策系统以及搜索引擎技术之中,推动了相关理论和应用技术的发展。
关键词:社会选择理论;集体决策;判断聚合方法;集体判断集;一致性
在社会生活中,人们时刻面临各种集体决策,比如换届选举、公共利益分配以及对服务体系的评价反馈等。社会选择理论研究的是如何将个体的意见、偏好以及判断聚合成集体决策,在公平公正基础上实现集体利益最大化。在这个领域有突出贡献的学者肯尼斯·阿罗(Kenneth Arrow)和阿玛蒂亚·森(Amartya Sen)都获得了诺贝尔经济学奖。社会选择理论涵盖了经济学、政治学、逻辑学、计算机科学与人工智能等多个领域,形成多学科交叉研究的局面。
一、问题的提出
社会选择理论用模型刻画社会选择过程。给定备选项集合X={a,b,c…}和个体集N={i1,…,in}(n≥3),个体根据自己的偏好对候选项集合X中的元素进行排序,得到个体偏好序列或者判断集,模型以个体偏好序或判断集作为输入,通过社会选择机制得到集体决策,社会选择机制通常表现为特定的聚合方法。
一般有三种社会选择模型:偏好聚合模型、投票模型以及判断聚合模型。偏好聚合模型(Preference aggregation model)首先需要每一个个体依据自己的偏好对备选项进行排序,形成个体偏好序列。偏好聚合规则规定了如何从所有个体序列中选择形成一个代表集体偏好的序列。[1]投票模型(Voting procedure)是偏好聚合模型的一种特殊情况,因为投票模型只要求选民投自己最喜欢的候选人,不用将其他的候选人依次排序。[2]判断聚合模型(Judgment aggregation model)则根据个体对议题进行判断所形成个体的判断集,运用聚合规则得到集体的判断。[3-4]
著名的“阿罗不可能定理”断定了把理性个体偏好聚合为理性集体偏好的不可能性。[1]阿罗定理的证明是无懈可击的,然而这个不可能的结论对任何集体决策都没有指导作用。我们需要更多切实可行的方法化解不可能的结论,得到相对公平公正的集体决策。判断聚合模型将聚合问题放入更为一般的逻辑框架之内进行研究,更加明晰地揭示了逻辑与集体理性聚合研究之间的密切联系,将集体理性聚合研究提升到一个更高的抽象水平。为此,本文将从判断困境这个经典案例出发,选取不同的判断聚合方法对集体判断不一致问题进行分析化解,在放宽了集体理性的前提下求得一致的集体判断集,使多主体决策成为可能。在应用方面,集体判断集代表集体决策为推荐系统(recommender systems)中的新用户提供推荐意见,同时集体判断集也可以作为搜索引擎的高频词汇为使用者提供精确的检索词。基于判断聚合模型化解不一致集体判断集的研究可以为个性化推荐和搜索工具方面的应用提供技术准备。
二、判断困境以及判断聚合模型
(一)判断困境
判断困境(discursive dilemma 或doctrinal paradox)[5-6]是孔多塞投票悖论在判断聚合理论中的变种,这个悖论是Kornhauser和Sager在1986年提出来的。由三位法官对一个是否违反合同的案件进行审理。依据法律的规定,如果合同是有效的(用p表示)且被告违反合同(用q表示),那么被告是有违约责任的(用r表示),这一法律规定可以符号化为“(p∧q)→r”。裁定被告违约责任要满足两个条件:第一,合同必须是有效的;第二,被告有违反合同的行为。这条法规对每位法官而言是公共知识,即它不需要裁决都得赞成。三位法官对案件的裁决实际上表现为依据法律规定(p∧q)→r对p、q和r这三个命题的投票。三位法官的个人裁决和集体裁决如表1所示。表1中用“1”表示赞同,“0”表示反对。

表1 判断困境
从表1中可以看出来,每一位法官的裁决都与法律规定相一致,因为与每位法官裁决相应的赋值都使公式(p∧q)→r为真。集体裁决依据的是多数规则,两人赞同合同是有效的p,两人赞同被告有违反合同的行为q,同时有两位反对被告有违约责任r,多数规则下的三位法官构成的集体所得的裁决结果是{p,q,r},这与法律规定相矛盾。因为,当p和q为真而r为假的时候,根据逻辑(p∧q)→r为假。这说明每一位法官的裁决都与法律相一致,多数规则又是公认的体现正义的聚合规则,但集体裁决却与法律规定矛盾。这个集体判断集显然不能作为最终裁决的结果。
判断困境提出之后引起了广泛的关注。政治学家菲利普·皮特(Philip Pettit)认为,这个悖论并非仅仅局限于法庭审判,可将它推广到任何的集体决策情形。[7]在判断困境下,得出理性的集体判断就成为不可能,但我们并不能因为个体理性的判断经过聚合之后得到非理性的集体判断就放弃寻找合理的集体判断,更不能因为这个集体判断与法律或者实际情况存在矛盾就否定社会选择的可能,这无异于因噎废食。现实生活中人们需要集体决策来分配资源,优化政治体制,提高服务质量,最大程度上体现公平公正,因而在实践层面我们需要分析不一致集体判断出现的原因,并寻找有效的判断聚合方法来化解不一致以求得合理的集体判断。为此,我们首先定义判断聚合模型,然后运用模型分析如何化解集体判断的不一致。
(二)判断聚合模型的定义
建立模型首先需要定义语言,我们用L来表示命题逻辑,它的语言L(L)具有一般命题逻辑的语义,其语法定义如下:

判断聚合模型的一个基本假设是:参与判断的所有的个体都是完全理性的,即作出的判断既是一致的又是完全的。所谓一致的是指作出的判断不能具有矛盾,所谓完全的是指对于所有待断定的命题都要作出判断。相关概念定义如下:
议题(Issue)指待判断的命题。显然,议题可以是L(L)中除了⊥外的任一命题。议题既不可以是重言式,也不可以是矛盾式,因为它们没有判断的必要。例如上述判断困境中的p、q和r是原子命题形式议题,当然也会有形如p∧q、p∨q或者(p∧q)↔r等复合命题形式的议题。
议程(Agenda)由议题以及议题的否定形式构成的集合称作议程,记作A。令φ是任一议题,则φ∈A当且仅当φ∈A,显然,A是非空的且A⊆L(L),双重否定可以抵消φ≡φ。对议程进行这样的规定是为了保证判断聚合中所要断定的命题都在议程中且是语言L(L)所能够刻画的。令[A]⊆A,但[A]中只包含议题本身,即A=[A]∪{φ∈[A]},这样的[A]称为预议程。设定[A]是为了方便后面的计算和说明。同理有子议程B是议程A的子集,即B⊆A,同时也有子预议程[B]⊆[A]。
一致性(Consistent)如果对于任一公式集S⊆L(L),如果不存在一个议题φ使得S├Lφ∧φ,则称S具有一致性或者说S是L-一致的。
完全性(Complete)对于任一公式集S⊆L(L),任一集合S⊆A,如果对于A中的议题φ∈A,φ∈S或者φ∈S,则称S具有完全性或者说S是完全的。
判断集(Judgmentset)判断集是与个体与集体相关的概念,用J表示。令N是参加判断的个体,N={1,2,…,n}(n≥2),则任一个体i(1≤i≤n)的判断集Ji是一个一致的且完全的集合,且Ji⊂A。判断集的一致性保证了个体或集体所作出的判断都是理性的,判断集的完全性保证了个体对议程中每一项议题都作出判断。本文中将所有的L-一致的判断集记作D(A),将所有L-一致且完全的判断集记作D(A),所以有D(A)⊂D(A)。
上述判断困境的例子中,所有的法官对议程中所有的议题进行断定的结果为:法官1的判断集J1={p,q,r,(p∧q)→r},法官2的判断集J2={p,q,r,(p∧q)→r},法官3的判断集J3={p,q,r,(p∧q)→r},而J1,J2,J3⊂D(A)⊂D(A)。
判断组合(Judgmentprofile)由所有个体的判断集组成的n元组称作判断组合,可表示为P=(J1,…,Jn)∈Dn(A)。我们用N(P,φ)表示判断组合P中有多少个个体的判断集中包含有φ,也就是N(P,φ)=#{i|Ji∈P,φ∈Ji},也称作议题φ的权重。
判断困境例子中所有法官的个体判断集分别是J1,J2和J3,判断组合就是由所有的法官的个体判断集组成的三元组P=(J1,J2,J3),计算这个判断组合P中支持“合同是有效的p”,N(P,p)=2,因为法官1和法官2支持p,法官3支持p,同理有N(P,q)=2和N(P,r)=2。
定义1判断聚合规则(Judgment aggregation rules) 令N是参加判断的个体集N= {1,…,n}(n≥3),议程A⊆L(L),J(A,L)表示议程A上所有判断集的集合,J(A,L)n表示所有个体的判断集构成的n元判断组合P=(J1,…,Jn)(Ji∈D(A))。一个判断聚合规则就是一个以J(A,L)n为定义域、以J(A,L)为值域的函数
根据聚合规则输出的判断集其性质的不同,可以分为两类判断聚合规则:
(a)确定性的判断聚合规则(deterministic judgment aggregation rule)。这一聚合规则输出的判断集是一致且完全的,即任一J∈J(A,L)都有J∈D(A)。
(b)不确定性判断聚合规则(Irresolute judgment aggregation rule)。这一聚合规则输出的判断集是一致的,但不一定是完全的,即任一J ∈J(A,L)都有J∈D(A)。

如何化解这一困境?研究文献[5,6,8]表明,有两种方法可以化解这一困境,分别是基于前提和基于结论的聚合方法。
(三)基于前提和基于结论的判断聚合规则解决判断困境
基于前提的判断聚合方法(premise-based procedure)和基于结论的判断聚合方法(conclusion-based procedure)[6-7]是在判断聚合理论发展初期由菲利普·皮特提出的。这两种方法的基本思想是通过将议程区分前提集和结论集,运用多数聚合规则分别对前提集和结论集中的议题进行聚合,从而化解集体判断的不一致的情形。这两种方法适用的范围是那些比较容易区分出前提集和结论集的议程。一般情况下我们主要依据逻辑语义来区分前提集和结论集。下面运用基于前提和基于结论的判断聚合方法分别对判断困境进行化解。
在判断困境例子中,预议程[A]={p,q,r,(p∧q)→r},其中复合命题(p∧q)→r的涵义是“如果有p并且有q,那么就有r”,即我们可以根据对(p∧q)→r以及p、q的断定,再运用命题逻辑推理规则推出是否有r这个结论,由此我们可以将预议程[A]区分为前提集的预议程[A]pr={p,q,(p∧q)→r}和结论集的预议程[A]c={r}。
(1)基于前提的判断聚合方法Fpr。大体说来,这一规则分两步运行:第一步,仅对前提集中的每项议题进行判断,采用多数聚合规则进行聚合;第二步,根据对前提集聚合得到的集体判断集,再运用命题逻辑推理规则推演出结论。也就是说,前提集中的一项议题是集体所肯定的当且仅当它是集体中多数人所肯定的;结论集中的议题是集体所肯定的当且仅当它是对前提集中议题的集体判断所能够演绎推出的。
既然仅对前提集中的议题进行判断,因此法官1、法官2和法官3的判断集分别变为J1={p,q,(p∧q)→r}、J2={p,q,(p∧q)→r}和J3={p,q,(p∧q)→r}。由于p在J1和J2中,q在J1和J3中,而(p∧q)→r在J1,J2和J3中,所以,p,q,(p∧q)→r∈JFpr,由其根据命题逻辑推理规则可推出结论r,所以r∈JFpr,即集体判断集JFpr={p,q,(p∧q)→r,r}。如表2所示,基于前提的判断聚合方法Fpr化解了基于多数聚合规则Fmaj的集体判断不一致。
在Fpr这个聚合方法中,个体判断仅对前提集[A]pr={p,q,(p∧q)→r}中的议题进行,所以个体判断集不是完全的,因此这一规则舍弃了个体完全理性。但集体判断集{p,q,(p∧q)→r}是一个L-一致且完全的判断集,因此集体是完全理性的。但这并不意味着Fpr聚合方法具有保持集体理性的性质。例如,当法官3对p的判定变为否定后,“p在J1和J2中”变成了“p在J1和J2中”,由此根据Fpr聚合得到的集体判断变为{p,q,(p∧q)→r},根据这样的前提无法推出r或者r。这使得集体对结论r无法判定,也就很难保持集体判断的完全理性。

表2 基于前提的判断聚合方法化解不一致集体判断集
(a)

[A]pr={pq(p∧q)→r}r法官1111-法官2101-法官3011-Fpr1111
(b)(2)基于结论的判断聚合方法Fc。这个方法仅仅考虑根据个体对结论集中议题的判断,按多数聚合规则得到集体对结论的判断,完全不考虑个体对前提集中议题的判断。如表3所示,基于结论的判断聚合方法Fc化解了多数聚合规则Fmaj中集体判断的不一致。

表3 基于结论的判断聚合方法化解不一致集体判断集
(a)

pq(p∧q)→r{r}法官1---1法官2---0法官3---0Fc---0
(b)显然,在Fc这一聚合方法中,所有判定都围绕结论的预议程集[A]c={r}进行。对结论r的集体判断是根据个体对r的判断和多数聚合规则得到的。由于法官2和法官3都反对r,“r在J1和J3中”,根据多数聚合规则得到集体对r的否定,即集体判断集JFc={r}。Fc聚合方法放弃了对个体判断和集体判断完全理性的要求,因为无论是个体判断集还是集体判断集,它们都是不完全的。
比较基于前提的判断聚合方法和基于结论的判断聚合方法,它们都是对完全理性要求作出修订得到一致的集体裁决,化解了集体判断的不一致难题。但是,这两种聚合方法都是有缺陷的。我们看到,运用Fpr和Fc各自得到的集体判断相互否定:运用Fpr可以得到“被告有违约责任”的集体判决,而运用Fc得到的是“被告没有违约责任”的集体判决。由于两种方法可选择,这意味着存在操纵集体判决的可能性。如何防止集体决策被操纵,保证决策结果公平公正地符合集体利益最大化的理性要求,是化解不一致难题必须考虑的问题。由于本文的重点是化解不一致,防操纵问题将在另外文章中专门讨论。
三、基于判断聚合模型化解集体判断不一致的问题
(一)不可区分为前提集和结论集的不一致集体判断
基于前提的判断聚合方法Fpr和基于结论的判断聚合方法Fc化解不一致,要求议题可以区分为前提集和结论集。然而很多的集体决策不满足这一要求。我们引入更为一般的议程,其中的议题没有办法区分前提或结论,同样是在运用多数聚合规则后得到的集体判断不是L-一致的。
例1给定预议程为[A]={p∧r,p∧s,q,p∧q,t},参与判断的投票者有17人,表4是这17位投票者给出的判断组合P。用“1”表示赞同,“0”表示反对。

表4 判断组合P
运用多数规则聚合后得出的集体判断集JFmaj={p∧r,p∧s,q,(p∧q),t},然而{p∧r,p∧s,q,(p∧q),t}├L(p∧p)或者{p∧r,p∧s,q,(p∧q),t}├L(q∧q),即这个集体判断不是L-一致的。因为,集体判断中有p∧r,而p∧r├Lp,即集体赞成p,集体判断中还有(p∧q),而(p∧q)├L(p∨q),即集体要么反对p,要么反对q,因为集体赞成p,可以推出集体反对q,而集体判断集中有q,即集体赞成q,这意味集体集赞成q又反对q,矛盾。再由集体判断集中有p∧s,而p∧s├Lp,即集体赞成p;集体判断中还有(p∧q)和q,而{(p∧q),q}├Lp,即集体反对p,这意味着集体既赞成p又反对p,矛盾。
因此,多数聚合规则Fmaj得到的集体判断集JFmaj∉D(A)是不正确的。然而,这个集体判断不是L-一致不能用基于前提的判断聚合方法和基于结论的判断聚合方法化解,因为预议程[A]={p∧r,p∧s,q,p∧q,t},我们根据逻辑语义无法区分哪些是前提哪些是结论,因此需要新的化解方法。
(二)基于多数判断集的判断聚合方法
基于多数判断集的判断聚合方法和基于权重最大判断聚合方法是法国逻辑学家吉罗姆·朗(Jerome. Lang)在2011年提出来的,主要是用于证明某些判断聚合规则在一定的限制条件下对应于特定的投票规则。本文中运用这两类方法的原理化解集体判断不一致问题。
基于多数判断集的判断聚合方法(Methods based on the majoritatian judgment set)[9-10]是通过最小化的信息损失得到L-一致的集体判断集。运用这一类方法来化解集体判断集的不一致,首先是改变原有议程中的议题,剔除部分导致集体判断集不一致的议题而形成一个新的子议程,删除要最大限度地保留原议程中的议题,使信息损失最小。然后基于子议程形成新的个体判断组合,再利用多数聚合规则对新的个体判断组合进行聚合,得到一个L-一致的集体判断。显然,这个L-一致的集体判断是原集体判断的一个子集。
有两种方法可以最小化损失信息得到L-一致集体判断:第一种是寻求一个原集体判断的最大L-一致子集;另一种方法是寻求一个原集体判断的基数最大L-一致子集。所谓基数(cardinal number)就是集合中元素的个数。现将两个概念定义如下:
定义3原集体判断最大一致子集原集体判断JFmaj⊆L(L),S是JFmaj的最大L-一致的子集,当且仅当,S是L-一致的,并且不存在一个L-一致的集合S′使得S⊂S′⊆JFmaj,即S是JFmaj的L-一致子集,并且不存在一个比S更大的L-一致的JFmaj子集。原集体判断JFmaj的最大一致子集记作JFMSA。
定义4原集体判断的基数最大L-一致子集原集体判断JFmaj⊆L(L),S是JFmaj的基数最大L-一致的子集,当且仅当,S是L-一致的,并且不存在一个L-一致的集合S′⊆JFmaj,使得S的基数小于S′的基数(|S|<|S′|)。即S是JFmaj一致子集,并且不存在一个比S基数更大的L-一致的JFmaj的子集。原集体判断的基数最大L-一致子集记作JFMCSA。
对应上面的两种方法,要想使得JFmaj由不一致变为一致,最大子议程的判断聚合方法就是对应于寻找原议程中最小删除部分议题而形成的子议程并且在这个子议程基础上使得集体判断是L-一致的;基数最大子议程的判断聚合方法是寻找原集体判断的基数最大且L-一致的子集,同样也是删除最小数目的议题形成新的子议程并且在此基础上得到L-一致的集体判断。删除过程要确保集体判断集基数最大。下面分别定义这两种方法并运用它们化解例1中的不一致集体判断集问题。
原集体判断集的最大L-一致子集是运用最大子议程的判断聚合方法得到的,而其基数最大L-一致子集则是通过基数最大子议程判断聚合方法得到的。
1.最大子议程的判断聚合方法
当多数判断聚合规则得到的集体判断集JFmaj不是L-一致时,运用最大子议程判断聚合方法(Maximal sub-agenda method,记作FMSA)化解集体判断集的不一致,首先要删除原议程中最少数量议题而得到一个原议程的最大子议程,然后基于子议程形成新的个体判断组合,再利用多数聚合规则对新的个体判断组合进行聚合,得到一个原集体判断集JFmaj的最大L-一致子集。下面举例说明化解过程。
例2仍用例1中的议程A和判断组合P,由多数聚合规则所得到的集体判断集JFmaj={p∧r,p∧s,q,(p∧q),t},根据我们前面对例1的分析,JFmaj不是L-一致的,现运用最大子议程判断聚合方法来化解这个不一致的集体判断集,删除议程中的议题q,做到最大限度保留原议程中议题。表5中“1”表示赞成,“0”表示反对,删除线表示剔除的议题以及相应的个体判断。
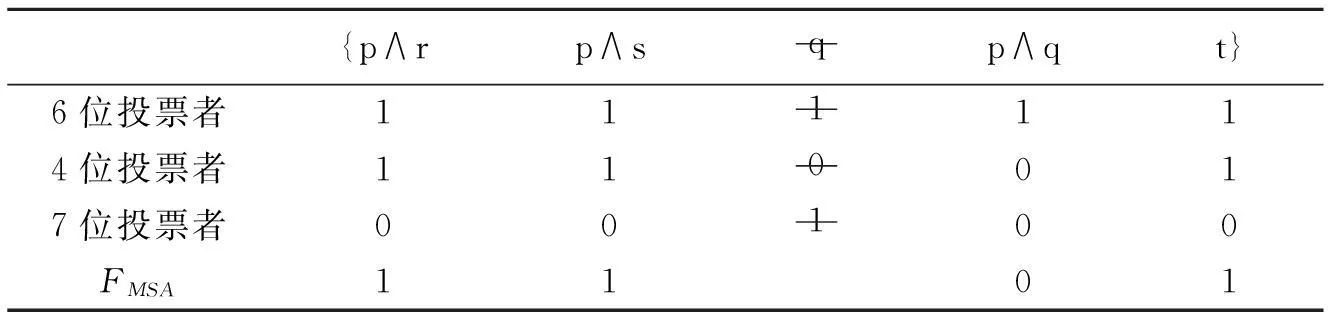
表5 最大子议程的判断聚合方法解决不一致集体判断集
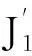
新的集体判断集JFMSA={p∧r,p∧s,(p∧q),t}是L-一致的,它化解了原集体判断集JFmaj={p∧r,p∧s,q,(p∧q),t}的不一致。它虽然不完全但符合不确定性判断聚合规则的要求J∈D(A),是正确的聚合结果。
JFmaj的最大一致子集并不是唯一的。请看表6。

表6 最大子议程的判断聚合方法化解不一致的集体判断
(a)
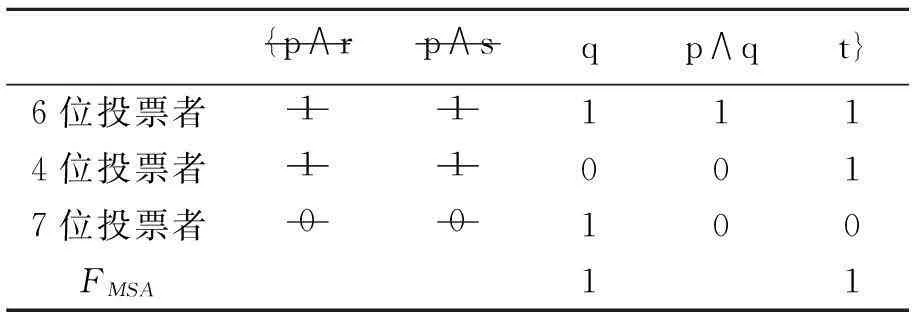
{p∧rp∧sqp∧qt}6位投票者111114位投票者110017位投票者00100FMSA11
(b)如表6中所示,(a)和(b)也是运用最大子议程判断聚合方法得到的L-一致的集体判断集:表6(a)是剔除了议题p∧q得到的集体判断集为{p∧r,p∧s,q,t}⊆JFmaj,这个集体判断集也是L-一致的;同理,表6(b)是剔除了议题p∧r和p∧s得到的集体判断集为{q,(p∧q),t}⊆JFmaj是L-一致的。我们看到这三种剔除议题的方法都可以得到L-一致的集体判断集。所以,最大子议程的判断聚合方法通过不同途径可以成功化解例1中所得到的不一致集体判断。
最大子议程判断聚合方法由不同的途径剔除议题,得到了不同的JFmaj最大L-一致子集。那么这些不同的子集中哪个更符合最小化信息损失的要求呢?最大子议程判断聚合方法没办法给出答案。基数最大子议程判断聚合方法则不同,它考虑了剔除议题的基数,基数是可以比较的,可以参考基数来判定哪种途径最大程度地保留了原议程中的议题,使得信息损失最小,因而集体判断更为合理。如果考虑基数,表6(b)中所示的剔除议题途径比起前两种是最劣的,因为它的集体判断集的基数最小,损失的信息最大。
2.基数最大子议程的判断聚合方法
基数最大子议程的判断聚合方法(Maxcardsub-agenda method)类似于最大子议程规则,同样是需要剔除导致不一致的议题,但它要保证集体判断集基数最大,也就是说要剔除最小数量的议题才能确保集体判断集中议题的个数最多。具体的方法是要根据最大子议程规则求得最大L-一致子集JFMSA,然后对各个最大L-一致子集的基数进行比较,删除最大L-一致子集JFMSA中基数最小的,剩下的就是基数最大的集体判断集JFMCSA,这也说明了JFMCSA⊆JFMSA。


表7 基数最大子议程的判断聚合方法化解不一致的集体判断
(a)

{p∧rp∧sqp∧qt}6位投票者111114位投票者110017位投票者00100FMCSA1111
(b)基数最大L-一致子议程的判断聚合方法化解集体判断的不一致,既得到了L-一致的集体判断,又确保了得到的集体判断集基数最大,也就是在确保最小化损失信息的基础之上得到了L-一致的集体判断集。因此,它是更合理的方法。
如果我们预设复合命题形式的议题包含的信息比原子命题形式的议题多的话,{p∧r,p∧s,(p∧q),t}这个集体判断集是最佳的选择,因为它只剔除了q这个议题得到基数最大且L-一致的集体判断集,也就是以最小的信息损失换取了集体判断的一致性。
最大子议程判断聚合方法和基数最大子议程判断聚合方法都是对议程中的议题进行了剔除以求得一致的集体判断集。对议程的议题剔除之后会导致个体判断集是不完全的,再根据FMSA和FMCSA聚合之后所得到的集体判断集也是不完全的,即最大子议程判断聚合方法和基数最大子议程判断聚合方法为了求得一致的集体判断集是舍弃了个体和集体的完全理性,是有缺陷的聚合方法。
(三)基于权重最大判断聚合方法
用最大子议程方法和基数最大子议程方法来化解集体判断的不一致都没有考虑到每一项议题所支持的人数,因此剔除q是达到集体判断一致的最佳选择,因为它损失信息是最小的。但是q的支持人数最多,这样的剔除是否符合大多数人的意愿值得怀疑。集体聚合问题时常需要考虑每一个议题、项目或者产品的支持或喜欢的人数。
基于权重最大判断聚合方法(method based on the weighted majoritarian judgment set)[9-10]是寻求在L-一致的集体判断的前提下,保留议程A中被最高人数所支持的那些议题。所谓权重(weight)就是议题的支持人数。一般情况下有两种方法可供选择:第一种是找到最多支持人数的议题形成子议程,然后考查在子议程上集体判断集的一致性,剔除那些导致不一致性的议题,将这个议题的否定放入集体判断集,得到的集体判断就是得票总数最多的判断集;另一种是对议程A中的议题按支持人数进行排序,集体判断集是要从这个排序中逐一放入每一项议题并考查集体判断集的一致性所得到的,最终得到的集体判断集是从支持票数最高到最低的议题构成的,如此既确保了一致性又考虑到了议题的支持人数。第一种被称作最大权重子议程方法,第二种被称作分级议程方法。其中,最大权重子议程方法在文献[11]中又被称为“简单得分规则(simple scoring rule)”,分级议程方法在文献[12]中又被称为“最小字典序规则(Leximin rule)”。
1.最大权重子议程方法

最大权重子议程方法(Maxweight sub-agenda method,记作FMWA)就是着重考虑议程每一项议题的权重和集体判断一致性的前提下,寻求最大权重L-一致集体判断集JFMWA的过程。用该方法化解例1中集体判断集不一致情形,首先要统计每一个议题支持的人数,也就是计算议题在判断组合中的权重,在此基础之上为找到一个总的支持人数最多且L-一致的集体判断集,将所有支持人数最多的议题纳入集体判断集,然后考查这个集体判断集的一致性。如果存在导致这个集体判断集不一致的议题,就将它的否定放入其中,最终得到的就是最大L-一致集体判断集JFMWA。用下面的例子来说明运用最大权重子议程方法化解例1中不一致集体判断集的过程。
例3仍用例1中议程集A和判断组合P。根据权重的定义,将每一项议题的权重计算如下:
依据最大权重子议程方法的定义,我们是要找到一个总的支持人数最多且L-一致的集体判断集,对以上每项议题的权重进行排序,得票最高的议题q是13票,其次(p∧q)是11票,然后是p∧r,p∧s和t各得10票,以此类推。现在要找到权重最大L-一致集体判断集JFMWA的话,首先要把支持人数最多的议题q放入JFMWA。考虑到一致性的要求,q和(p∧q)不可以放入JFMWA,因为,已经放入q,自然不能有q;而如果将(p∧q)放入其中,就会影响p∧r和p∧s放入JFMWA,因为{p∧r,p∧s,(p∧q)}├L(p∧p),即存在逻辑矛盾,但可以将(p∧q)的否定p∧q放入JFMWA并不会导致逻辑矛盾;紧接着我们把三项支持人数为10的议题p∧r、p∧s和t放入集体判断集JFMWA中,这三项议题的加入并没有导致JFMWA不一致情况的发生。同理考虑到一致性的问题,他们的否定形式的议题(p∧r)、(p∧s)和t都不可以放入集体判断集JFMWA中,因而运用最大权重子议程方法得到的集体判断集JFMWA总的权重为WP({q,p∧q,p∧r,p∧s,t})=13+6+10+10+10=49,这个集合是在一致性的条件下权重最大的集体判断,没有其他的集体判断集比这个集合权重更大,因而,求得的JFMWA={p∧r,p∧s,q,p∧q,t}是权重最大L-一致判断集。FMWA方法是合理地解决不一致集体判断的方法。
运用最大权重子议程方法得到集体判断集JFMWA是总的支持人数最多L-一致的判断集,同时这个集合也是完全的,因而,我们说基于最大权重的子议程方法是最大限度地考虑了个体的意见得到的集体判断集。然而,最大权重子议程方法着重考虑了求得的集体判断集总的支持人数是最大的,没有考虑到是否每一项议题的支持人数都是最大的。在上面的例子中,支持人数排名第二的议题(p∧q)由于影响了集体判断集JFMWA的一致性只能将它的否定形式放入其中,剔除了(p∧q),这样所得的集体判断集也是有瑕疵的。如何才能最大程度地保留支持人数最多的议题,需要引入分级议程方法来解决这个问题。
2.分级议程方法
定义6议题权重最大L-一致集体判断集(JFRA)任一议程A={ψ1,…,ψ2m}以及对应的排列σ为{1,…,2m},P是A上的判断组合,令≥为议程A上的完全弱序的偏好关系,即对于任意议题φ和ψ,如果N(P,φ)≥N(P,ψ),那么φ≥ψ,因而可得如果ψσ(1)>…>ψσ(2m),那么ψ1…ψ2m。下面来定义议题权重最大L-一致集体判断集JFRA:J∈JFRA当且仅当存在一个序列σ使得>对应于并且J=Jσ通过以下过程获得:
S0:=ø;
对于任何j=1,…,2m,如果Sj-1∪{ψσ(j)}是L-一致的,那么Sj:=S∪{ψσ(j)};
逐一放入ψσ(j)直到最后一项;
Jσ=S
运用分级议程方法(Rank agenda method,记作FRA)找到集体判断集JFRA类似于形成极大一致集的过程。首先要计算议程中每个议题的权重,找到议题权重从大到小的≻排序,从而得到相应的议题的偏好排序。考查每一个议题ψσ(j)放入JFRA中时的一致性,最终得到议题权重最大L-一致集体判断集JFRA。下面举例说明运用分级议程方法化解例1中不一致的集体判断集的过程。
例4我们依然用例1中的议程A和判断组合P。现在要用分级议程方法FRA来解决集体判断的不一致。
首先,计算议程中所有议题的权重:N(P,p∧r)=10,N(P,(p∧r))=7;N(P,p∧s)=10,N(P,(p∧s))=7;N(P,q)=13,N(P,q)=4;N(P,p∧q)=6,N(P,(p∧q))=11;N(P,t)=10,N(P,t)=7。
运用分级议程方法解决集体判断不一致的情况,首先考虑的是每一项议题支持人数的多寡,也就是每项议题的权重,其次在形成JFRA的过程中,除了考虑到了集体判断集的一致性,也同时顾及到了完全性的要求,所得到的集体判断集是L-一致且完全的。
最大权重子议程方法和分级议程方法都考虑到了议题支持人数的信息,并且得到的集体判断集都是L-一致且完全的。为了化解不一致的集体判断集,这两种方法都对议程中每一项议题的权重进行了计算。然而在运用FMWA和FRA过程中并没有考虑到个体判断集是否是L-一致且完全的,也就是没有将个体的完全理性考虑在内,所得到的集体判断集是符合完全理性要求的,因而这两种方法是修改了个体完全理性的要求得到一致且完全的集体判断集,也是有缺陷的聚合方法。
四、结语
本文在判断聚合框架下分析了集体判断不一致的问题以及相应的解决方案。通过探讨,得出如下的结论:第一,议程中的议题可以明确区分前提集和结论集的情况,采用基于前提或者结论的判断聚合方法来得到一致的集体判断。这两种方法在处理不一致集体判断集的过程中,个体单独对前提集或者结论集进行判断,然后再使用多数聚合规则从而化解不一致的集体判断集。第二,议程中的议题不易区分前提集和结论集的情况下,本文主要采用基于多数判断集的判断聚合方法和基于权重最大的判断聚合方法。从上述的分析来看,这两类方法对这种无法区分前提集和结论集的不一致集体判断集是行之有效的。基于多数判断集的判断聚合规则侧重考虑的是删除部分议题来化解不一致的集体判断集,剔除议题的原则是最大程度保留原议程中的议题;基于最大权重子议程的判断聚合规则着重考虑每个议题支持人数的多少,尽量确保集体判断集中保留支持人数多的那些议题。第三,每一种判断聚合方法都不是全能的,它们都存在各自的缺陷,选择不同的方法聚合会导致不同的集体判断集,这也同时表明任何聚合方法都不是完美的,都存在被操纵的可能性。
判断聚合方法与投票规则有着千丝万缕的联系。判断聚合方法是投票规则的一般和概括,对判断聚合方法的某些限制条件的改变会对应于某些投票规则。在未来的研究中,我们可以证明哪些限制条件下的判断聚合方法可以对应于我们已知的一些投票规则。除此而外,判断聚合规则本身也还有很多新内容可以挖掘,本文中所采用的一种是区分前提结论,另外一种是对议程中议题的取舍。接下来也可以对个体判断集进行取舍或者改变从而达到一致的集体判断,或者采用信念融合过程中的基于距离的融合算子设计判断聚合方法,对判断组合进行更改从而达成一致的判断结果。我们可以在研究判断聚合方法的过程中深入考查这些规则所满足的性质,比如一致同意原则、单调原则、可分离原则等等,以及在何种情况下会导致不可能情形的发生。
总之,现在新出现的一些计算机科学的新技术需要聚合个体的信息或者判断,社会选择理论提供这样的方法和技术,特别是判断聚合理论的出现和发展对计算机和多主体决策系统提供了新的更准确的聚合方法。我们可以利用这些模型聚合个体判断得到集体的决策,从而可以将集体的判断内容推荐给更多的个体,服务于更多更广泛的个体来解决信息过载(information overload)的问题,这就是在推荐系统中的应用。对于搜索引擎用户搜索内容的聚合,区分不同类型用户得到某一类用户的搜索内容排序,使得用户更快地搜索到所需内容。随着电子商务和互联网的不断发展,判断聚合理论的方法与人工智能技术的结合将做出很多类似推荐系统和搜索引擎的应用,可以更好更便捷地服务人类生活。
参考文献:
[1]ARROW K. Social choice and individual values[M]. Wiley, 1951.
[2]BRAMS S, FISHBURN P. Voting procedures[M].Handbook of social choice and welfare: 2002, 1:173-236.
[3]LIST C. The theory of judgment aggregation: An introductory review[M]. Synthese, 2012:179-207.
[4]LIST C, PUPPE C. Judgment aggregation: a survey[M]. Oxford University Press, 2007.
[5]KORNHAUSER L, SAGER L. Unpacking the court[J].Yale LJ, 1986, 96:82-117.
[6]KORNHAUSER L, SAGER L. The one and the many: Adjudication in collegial courts[J]. California law review, 1993, 81:1-1657.
[7]PETTIT P. Deliberative democracy and the discursive dilemma[J].Philosophical issues, 2001,11(1):268-299.
[8]KORNHAUSER L. Modeling collegial courts ii: Legal doctrine[J]. Journal of law, economics and organization, 1992,8: 441-470.
[9]LANG J, PIGOZZI G, SLAVKOVIK M, TORRE L. Judgment aggregation rules based on minimization[M]. Proceedings of the 13th conference on theoretical aspects of rationality and knowledge, ACM, 2011:238-246.
[10]LANG J, SLAVKOVIK M. Judgment aggregation rules and voting rules[M]. Algorithmic decision theory, springer, 2013: 230-243.
[11]DIETRICH F. Scoring rules for judgment aggregation[J].Social choice and welfare, 2014,42(4): 873-911.
[12]NEHRING K, PIVATO M, PUPPE C. Condorcet admissibility: Indeterminacy and path-dependence under majority voting on interconnected decisions[M].University library of munich, 2011.
责任编辑刘荣军
网址:http://xbbjb.swu.edu.cn
中图分类号:B81
文献标识码:A
文章编号:1673-9841(2016)01-0018-11
基金项目:西南大学人文社会科学重大培育项目“中国社会转型下群体理性认知的逻辑分析及实证建模研究”(12XDSKZ003),项目负责人:唐晓嘉。
通讯作者:
作者简介:李莉,西南大学逻辑与智能研究中心,博士研究生。唐晓嘉,教授,博士生导师。
收稿日期:*2015-05-07
DOI:10.13718/j.cnki.xdsk.2016.01.003

