混凝土收缩徐变B3模型的修正与验证

齐金振，朱劲松,2

（1.天津大学建筑工程学院，天津300072；2.滨海土木工程结构与安全教育部重点实验室，天津300072）

混凝土收缩徐变B3模型的修正与验证

齐金振1，朱劲松1,2

（1.天津大学建筑工程学院，天津300072；2.滨海土木工程结构与安全教育部重点实验室，天津300072）

对国际上认可程度较高的B3模型进行了形式的修正，解决了其含有不可积分系数、不能进行连续计算的弊端，给出了混凝土收缩徐变修正模型表达式．使用控制变量法分析了影响混凝土收缩徐变各因素的敏感度，并利用多组试验数据对修正模型进行了验证．结果表明：对于徐变系数而言，修正公式所得结果与B3公式所得结果趋势一致，数值差别不大，且修正公式所得结果与试验实测值更接近，其拟合效果要优于JTGD62-2004模型；对于收缩应变而言，修正公式所得结果与B3公式所得结果趋势一致，且数值差别不大．

混凝土；收缩徐变；B3模型；修正模型

0 引言

混凝土的收缩和徐变是混凝土材料本身固有的时变特性，它会导致混凝土结构的受力与形变随着时间的推移而呈现出规律性的变化，准确掌握混凝土收缩和徐变特性对研究在役混凝土结构的服役性能具有重要意义．

随着研究的深入，混凝土收缩徐变的机理已被揭示，收缩徐变的结构效应分析方法也得到了很大发展[1]．欧洲混凝土委员会及许多国家设计规范都对混凝土收缩徐变给出了模式规范，包括：CEB-FIP系列模型、ACI209系列模型、BP系列模型、GL2000模型、JTG D62-2004模型[2]等．这些模型都是根据大量试验数据，结合收缩徐变的机理拟合而得到的．由于各模型公式推测的出发点和考虑的因素不尽相同，针对同一构件，不同预测模型给出的计算结果是不同的．此时需要选定一种适用性广泛、计算结果相对准确的预测模型，来计算混凝土结构收缩徐变的时变特性．文献表明，模型解析解与试验数据实测值符合程度最高的是Bazant教授于1995年提出的B3模型[3]．然而，由文献[3]可知，B3预测模型形式复杂，且其基本徐变度中包含有不可积分项Q t,，不能进行连续计算，不能快捷应用于工程实际计算．

本文从减小工作量及实现连续计算的需求出发，将B3模型修正为结构简便的多系数相乘的形式，提出了基于B3模型的修正模型，并采用文献[4-6]中的试验实测数据对修正模型进行验证．

1 B3模型简介

1979年，Bazant等利用电子计算机对世界各国收缩徐变的庞大数据进行了最佳拟合分析，并在此基础上提出了B-P模型及BP2模型（对B-P模型的简化）．1995年Bazant又提出了改良的、更符合实际的B3模型[3]．作为国际材料与结构研究试验室联合会（RILEM）的建议方法，B3模型综合考虑了混凝土水泥含量、水灰比、骨料水泥重量比等混凝土配比情况，对混凝土收缩与徐变的预测均较合理．

1.1 徐变模型表达式

B3模型中用徐变函数表示单位应力下的总应变，将徐变分为基本徐变和干燥徐变，且都有其具体的数学表达式：

徐变函数表达式为

基本徐变度

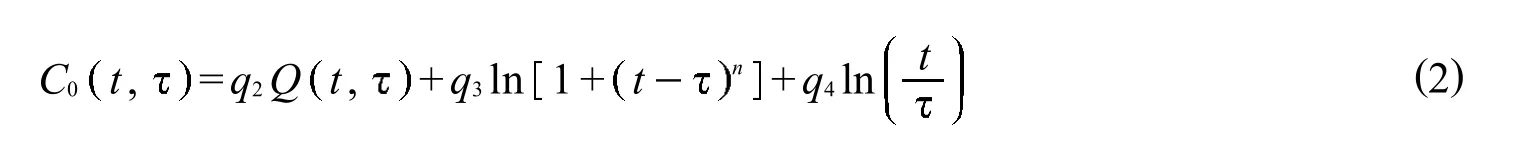
干燥徐变度

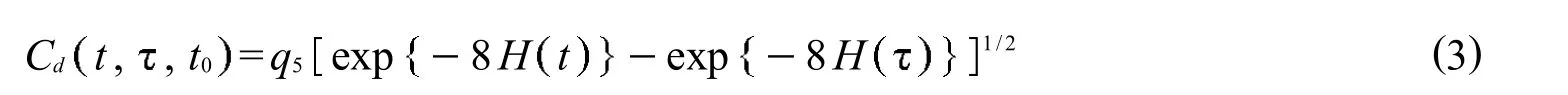
徐变系数表达式

式中：q1为单位应力产生的瞬时应变；q2，q3，q4，q5，H t，H，E是与构件材料组成相关的系数，其值可由文献[3]中公式求得；Q t,是没有解析解的二项式积分，其数值需在文献[3]中查表得到．1.2收缩模型表达式

收缩应变表达式为

时间曲线

式中：sh为收缩终极值，kh为与环境相对湿度有关的函数，sh为与构件尺寸有关的函数，其表达式都可由文献[3]查得．

由文献[3]可知，B3模型采用的是英制单位，其中长度单位为inch（1 inch=25.4mm），材料含量单位为bft3（1 bft3=16.03 kgm3），混凝土强度单位为psi（1 psi=6 895Pa）．

2 修正徐变模型表达式

2.1 修正徐变公式的标准形式

为了解决B3模型中含有不可积分系数的弊端，本文以B3模型为基准，将B3模型修正为结构简便的多系数相乘的形式．作为基准的B3模型材料参数取值如下：

混凝土强度等级为C40，材料配比为水泥∶砂子∶碎石∶水=1∶1.204∶2.963∶0.389，环境相对湿度为60％，构件体表比v/s=25.4mm，混凝土圆柱体抗压强度标准值f'c=0.85 f'cu,k[7]．本文将基准条件下徐变系数基本方程调整为

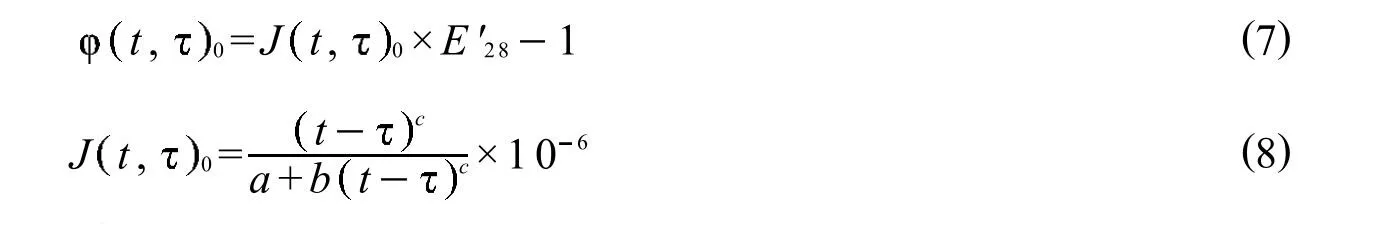
式中：为加载龄期，此处取7 d；J t,0为基准条件下加载龄期为时，t时刻的徐变函数；t,0为基准条件下加载龄期为时，t时刻的徐变系数；E'28为英制单位下28 d混凝土弹性模量E'28=E28×106/6895，其中E28为28 d混凝土弹性模量（MPa）；a、b、c为待定系数，其值可利用基准条件下B3模型的计算结果经回归分析确定．

混凝土的徐变效应随计算龄期ti的增长而单调递增，但增长速度逐步变缓，因此确定时间序列t1,t2, tn时，应使时间序列先密后疏，时间间距逐步加大[8]．给定第1次计算龄期t1=7.1 d，第2次计算龄期t2=7.2 d，其它时间可按以下方法确定：

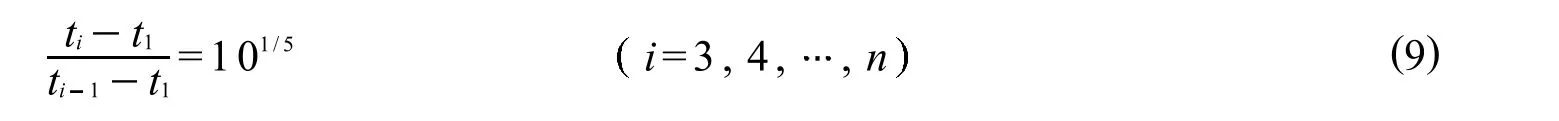
按此法确定的从7.1 d到100 a（365 00 d）的时间序列，及按这个时间序列由式(1)确定的数据样本见表1．由表1给定的数据样本，拟合公式(8)，回归分析得a=2.668，b=0.271，c=0.071，标准差s=1.32 ×105，相关系数为r=0.997．则式(8)可写作

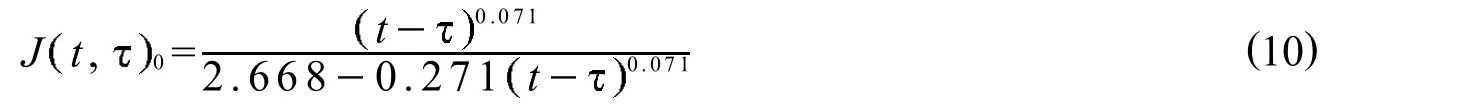
公式(10)计算结果也列于表1中，由表1及图1可知，公式(10)计算的修正B3模型徐变函数值与公式(1)计算的B3模型徐变函数值拟合效果非常好，相对误差都在6％以内，完全可以接受．

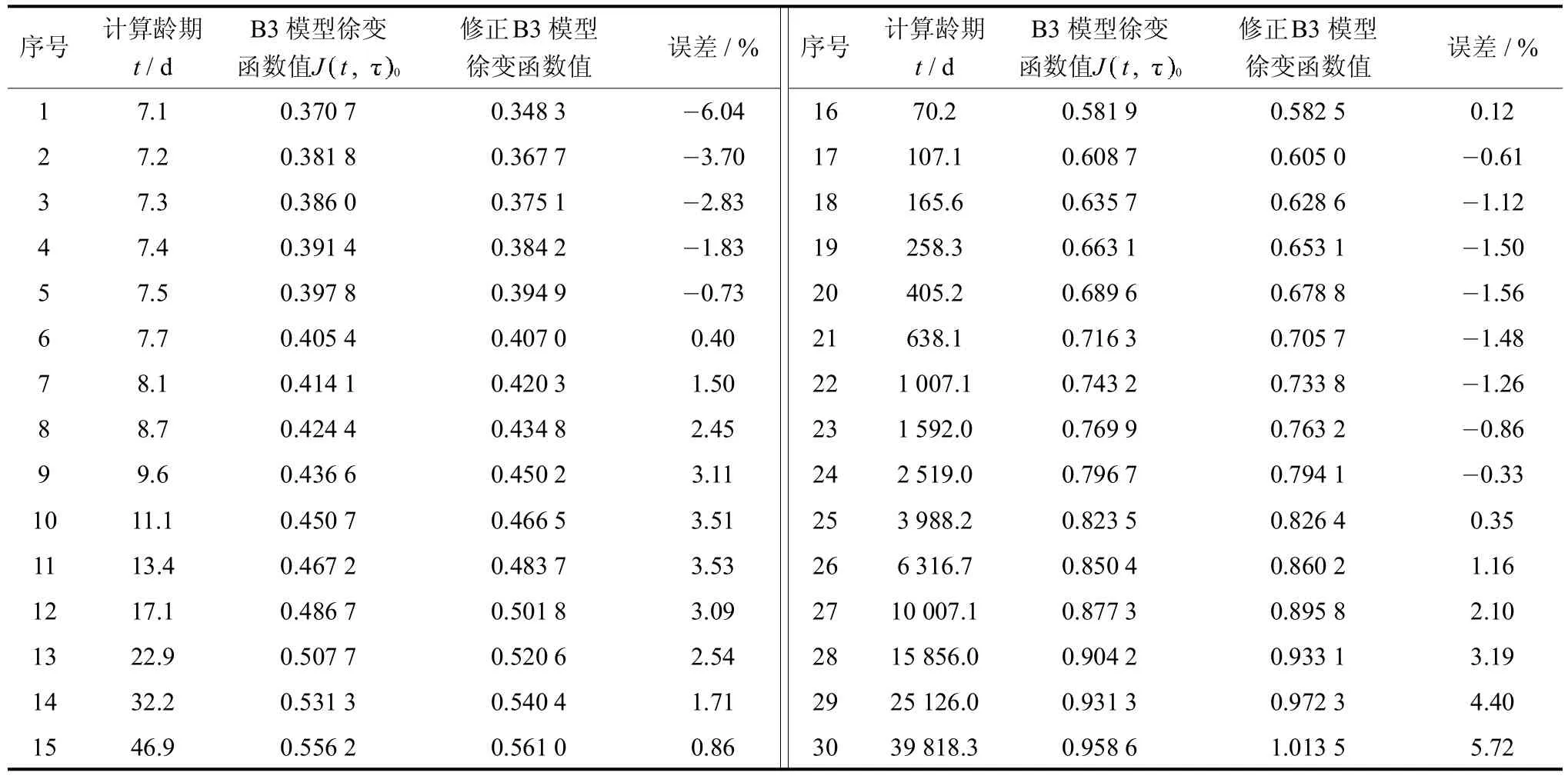
表1 修正B3模型徐变函数值与B3模型徐变函数值比较Tab.1 Comparison betweenmodifiedmodel B3 creep function value andmodel B3 creep function value

影响混凝土徐变的因素有很多，主要有：构件加载龄期、尺寸、工作环境的温湿度、水泥用量、水灰比、集料种类及混凝土强度等级等[1]．当混凝土徐变效应有关影响因素改变时，可按下式计算徐变函数

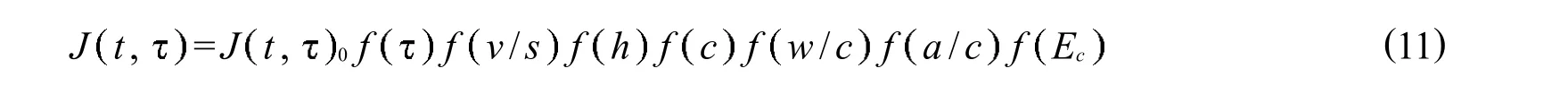
式中：J t,0为基准条件下徐变随龄期t发展的基本函数方程；f为加载龄期对徐变函数的影响函数；f为构件体表比V/S(mm)对徐变函数的影响函数；f h为环境相对湿度h（取小数）对徐变函数的影响函数；f c为水泥含量（kg m3）对徐变函数的影响函数；f w/c为水灰比对徐变函数的影响函数；f a/c为水泥骨料比对徐变函数的影响函数；f Ec为混凝土弹性模量（GPa）对徐变函数的影响函数．

2.2 各影响因素的影响函数表达式

相关研究表明[9]，在持荷时间、构件截面尺寸、构件材料成分、相对湿度及混凝土强度等级等条件不变的情况下，混凝土的加载龄期越大，混凝土的徐变函数值越小．因此，可以认为，当持荷时间t无限大时，混凝土的加载龄期越大，混凝土的徐变函数极值越小．参照B3模型，以7 d龄期加载为基准，加载龄期的影响函数如表2中所示．

以不同持荷龄期下的不同体表比取值下的徐变函数平均值与该龄期下的基准体表比下的徐变函数的比值来拟合构件体表比对徐变函数的影响函数．构件体表比的影响函数如表2中所示．

构件所处环境相对湿度、水泥含量、水灰比、骨料水泥重量比及混凝土强度等级的影响函数计算过程同构件体表比的计算过程，各表达式也一并列入表2中．

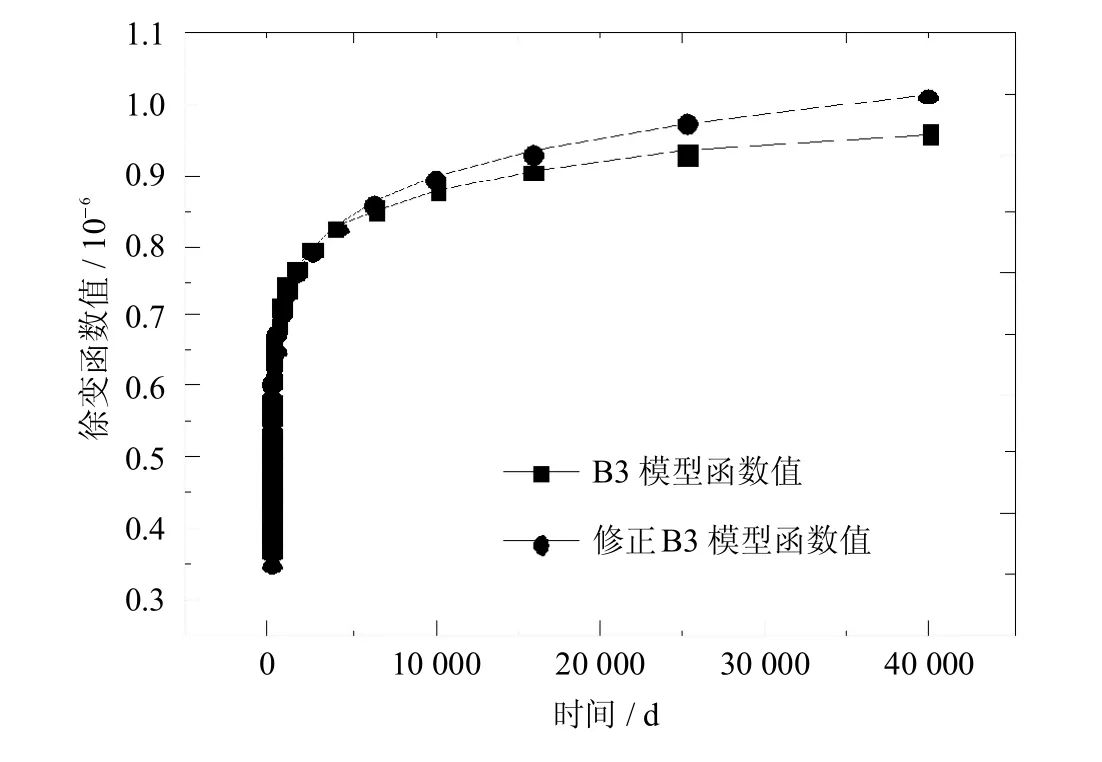
图1 修正B3模型徐变函数值与B3模型徐变函数值比较Fig.1 Comparison betweenmodifiedmodelB3 creep function value andmodelB3 creep function value

表2 徐变各影响因素函数表达式Tab.2 Function expression ofeach factorof creep

2.3 其他因素的影响函数表达式

混凝土养护方法对混凝土徐变的影响函数的取值可以按照中国建科院(1986)模型规定取值，即

2.4 修正徐变模型表达式

综上所述，修正徐变模型表达式可以表示为

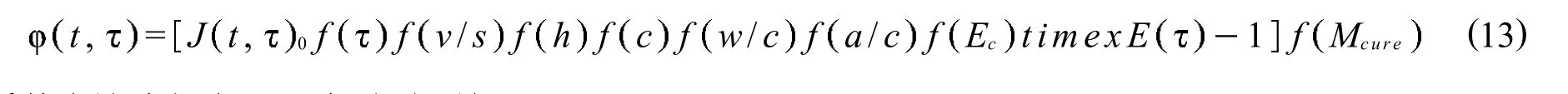
式中各系数表达式如表2及式(12)所示．

3 修正收缩模型表达式

3.1 修正收缩公式的标准形式

此处，参照上述混凝土修正徐变模型公式的推导办法，直接求解得出混凝土收缩随时间发展的基本方程：

3.2 各影响因素的影响函数表达式

构件加载龄期、构件体表比、环境相对湿度、构件含水量、混凝土强度等级、混凝土养护方法、水泥种类等对构件收缩应变的影响函数表达式如表3中所示．

表3 收缩各影响因素函数表达式Tab.3 Function expression ofeach factorof shrinkage

综上所述，混凝土修正收缩模型计算公式为：

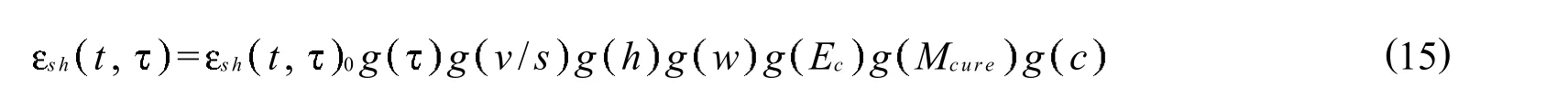
式中：sht,0为基准条件下收缩随龄期t发展的基本方程，按式(14)计算；g为加载龄期对收缩的影响函数表达式，按表3中表达式计算；g v/s为构件体表比v/s(mm)对收缩的影响函数表达式，按表3中表达式计算；g h为境相对湿度h（取小数）对收缩的影响函数表达式，按表3中表达式计算；g为水含量对收缩的影响函数表达式，按表3中表达式计算；g Ec为混凝土弹性模量（GPa）对收缩的影响函数表达式，按表3中表达式计算；g Mcure为混凝土养护方法对收缩的影响函数表达式，按表3中表达式取值；g c为水泥种类对收缩的影响函数表达式，按表3中表达式取值．

4 修正模型公式的验证及校核

为了检验该修正公式的可行性，本文运用文献[7-9]中的试验数据进行修正公式的验证及校核．本文采取的对比模型是B3模型以及广泛应用于我国工程实际计算的中国交通部颁布的《公路钢筋混凝土及预应力混凝土桥涵设计规范》中的JTG D62-2004模型．

4.1 普混凝土收缩徐变试验数据对比

叶列平等[7]进行了普通混凝土C40试件的徐变试验及普通混凝土C40、C50、C60试件的收缩试验，试验采用标准条件进行．将文献[7]所得试验实测徐变、收缩值与相对应的本文修正B3模型值、B3模型值及JTG D62-2004模型值对比，对比结果如图2～图5所示．

由图2可见，对于徐变系数而言，该修正公式所算结果与B3公式所算结果趋势一致，且数值差别不大，且该修正公式所算结果与试验实测值更加接近，并且其拟合效果要远好于JTGD62-2004模型；由图3～图5可见，对于收缩应变而言，该修正公式所算结果与B3公式所算结果趋势一致，且数值差别不大，但JTG D62-2004模型计算结果与实测值更接近．

4.2 C60低收缩徐变混凝土收缩徐变试验数据对比

陈露一等[8]以不同配合比的C60混凝土试件为试验对象，分别进行了7组收缩徐变试验．本文选取其中S1、S2、S4共3组试件为研究对象，具体配合比情况参见文献[8]．其中徐变试验试件的尺寸为100mm ×100mm×400mm，标准养护24 h后脱模，28 d后移入徐变室．收缩试验试件同徐变试验试件，收缩变形值通过外装式千分表测得．将文献[8]所得试验实测徐变、收缩值与相对应的本文修正B3模型值、B3模型值及JTG D62-2004模型值对比，对比结果如图6～图11所示．

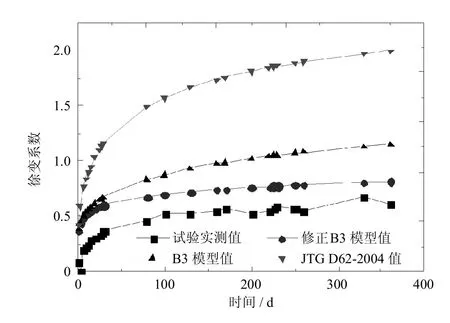
图2 N40-C试件徐变数据对比Fig.2 Comparison of specimen N40-C creep data

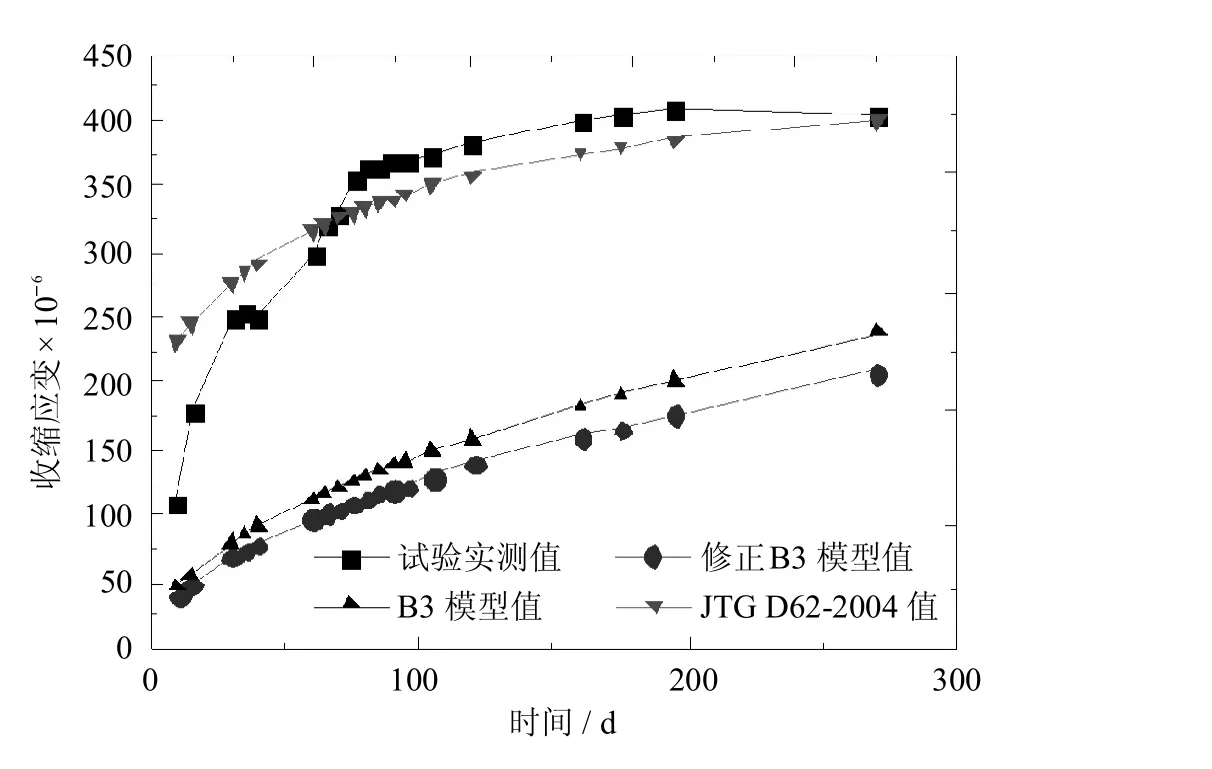
图3 N40-S试件收缩数据对比Fig.3 Comparison of specimen N400-Sshrinkage data

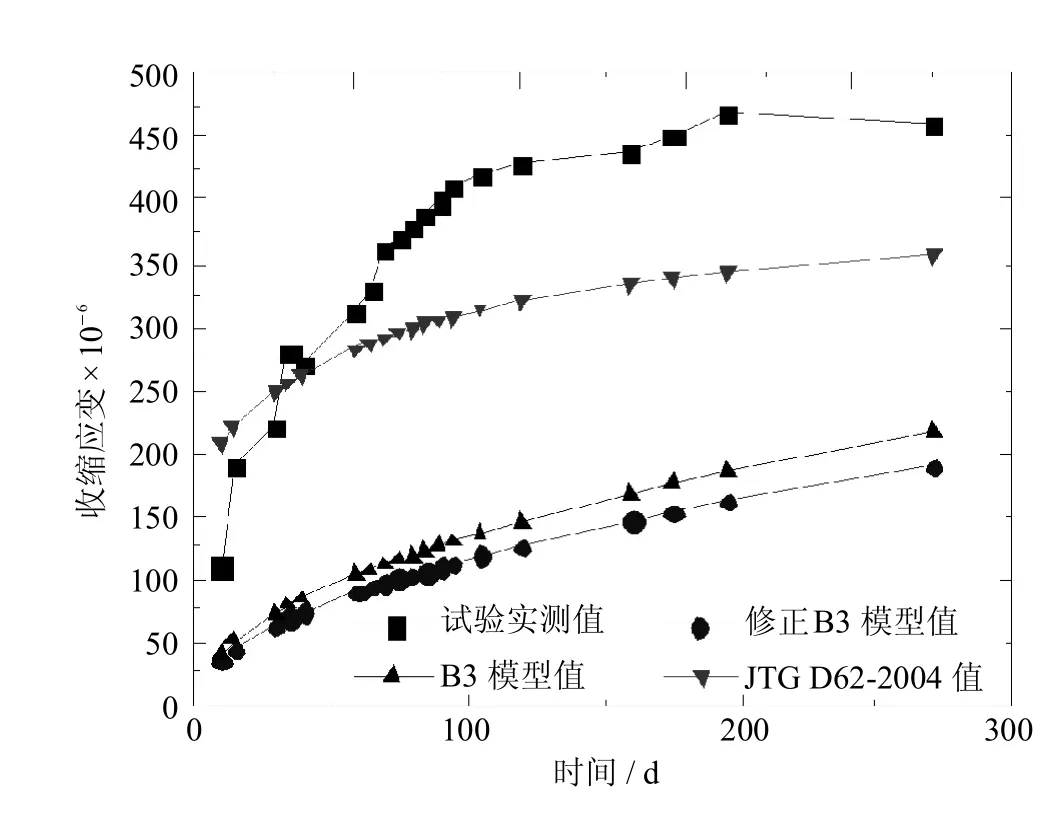
图4 N50-S试件收缩数据对比Fig.4 Comparison of specimen N50-Sshrinkage data

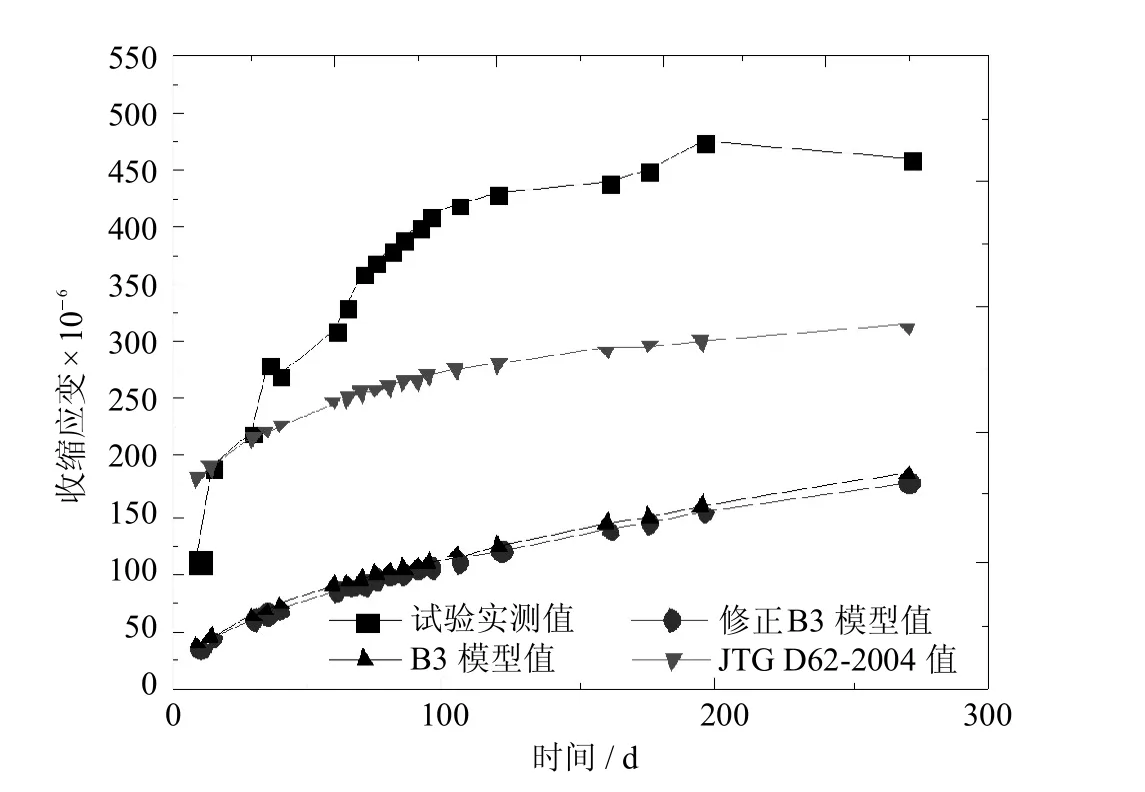
图5 N60-S试件收缩数据对比Fig.5 Comparison of specimen N60-Sshrinkage data

由图6～图8可见，对于徐变系数而言，该修正公式与B3公式所算结果趋势一致，数值差别不大，但该修正公式所算结果变化趋势与试验实测值变化趋势更接近，能较好的反映其变化规律，并且其拟合效果要优于JTGD62-2004模型；由图9～图11可见，对于收缩应变，该修正公式与B3公式所算结果趋势一致，且数值差别不大，但JTG D62-2004模型计算结果与实测值更接近．

4.3 高强混凝土收缩徐变试验数据对比

潘钻峰等[9]以苏通大桥辅桥连续刚构桥所用不同强度等级高强混凝土试件为试验对象，分别进行收缩徐变试验．其中徐变试验试件的尺寸为100 mm×100 mm×300 mm，分3组，每组2个试件，在标准养护室分别养护至3 d、7 d、14 d后，移至徐变实验室进行加载，加载应力水平为混凝土同期轴心抗压强度的0.4倍．收缩试验尺寸及养护条件分别为：100mm×100mm×400mm并标准养护至7 d后移入恒温恒湿室开始干燥；150mm×150mm×450mm并标准养护至7 d后移入恒温恒湿室开始干燥；100mm×100mm× 400mm并标准养护至14 d后移入恒温恒湿室开始干燥．将文献[9]所得试验实测徐变、收缩值与相对应的本文修正B3模型值、B3模型值及JTGD62-2004模型值对比，对比结果如图12～图17所示．

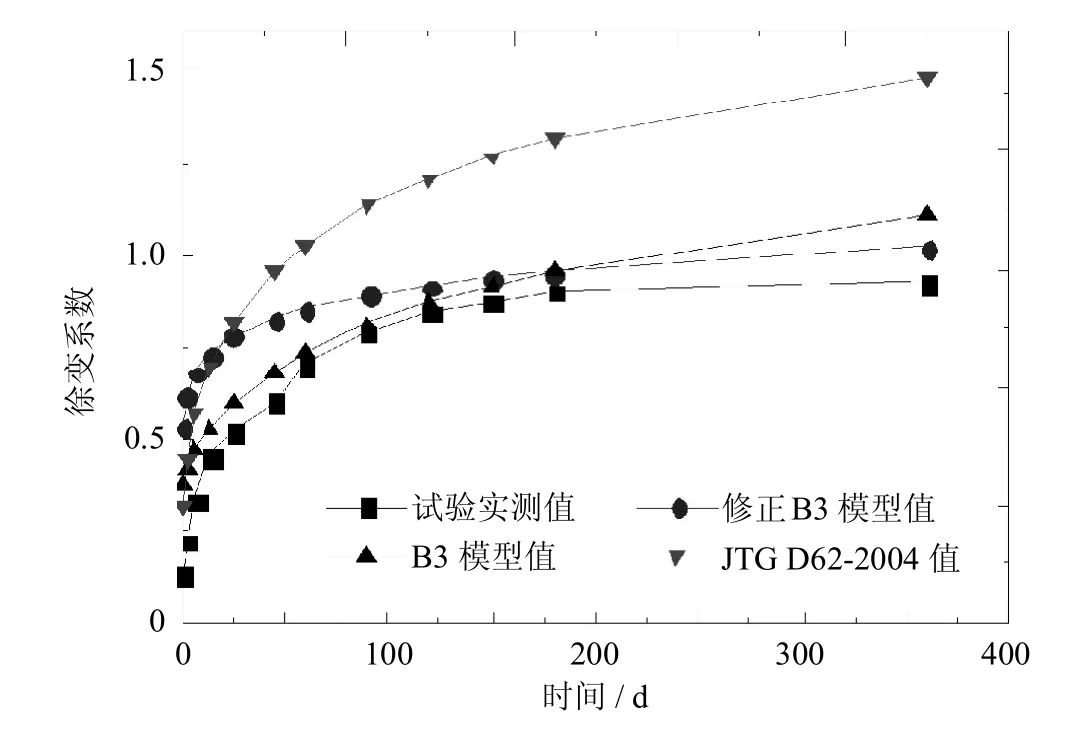
图6 S1试件徐变数据对比Fig.6 Comparison of specimen S1 creep data

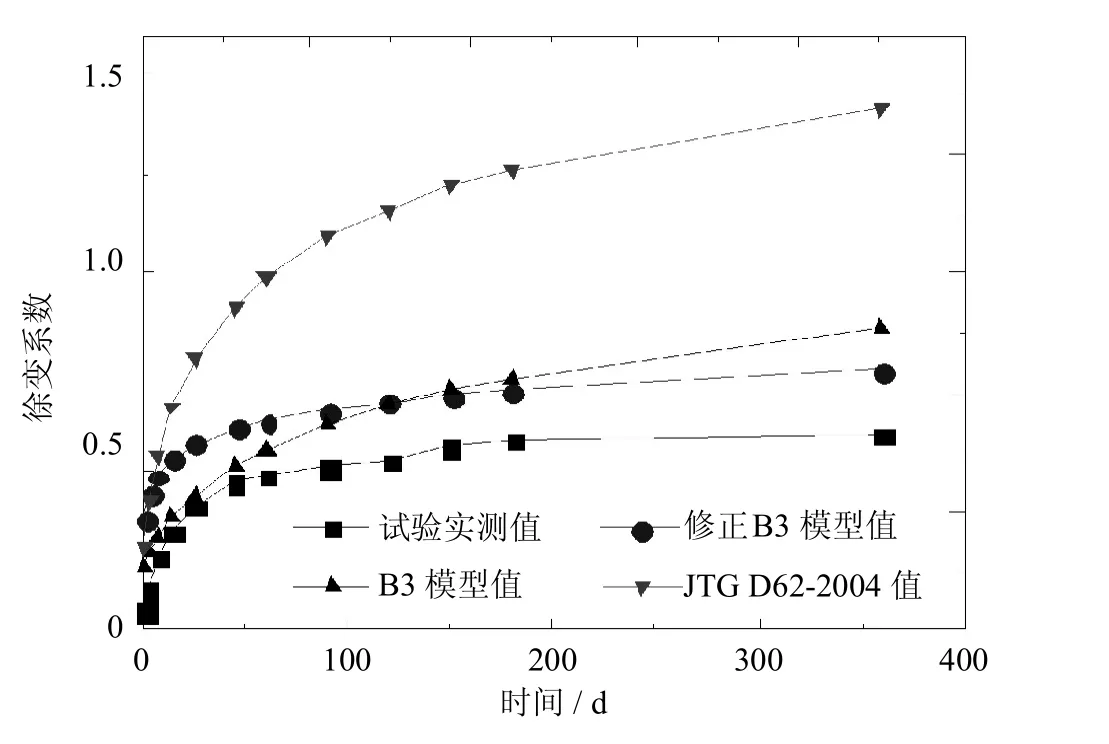
图7 S2试件徐变数据对比Fig.7 Comparison of specimen S2 creep data

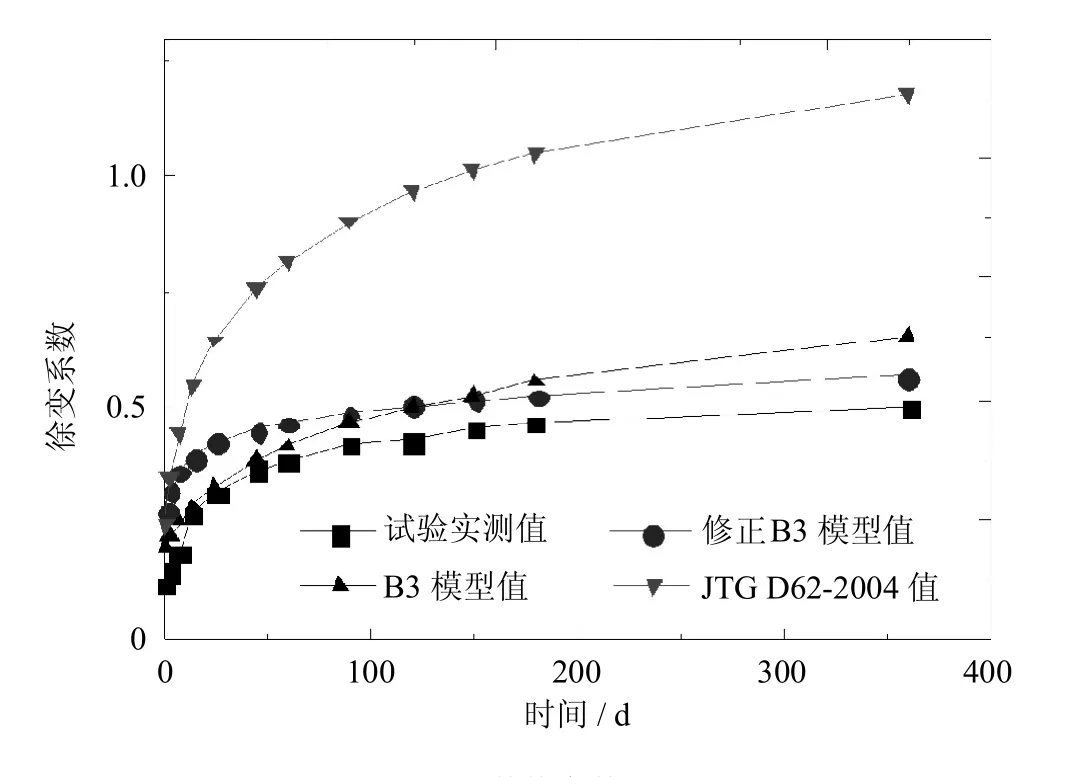
图8 S4试件徐变数据对比Fig.8 Comparison of specimen S4 creep data

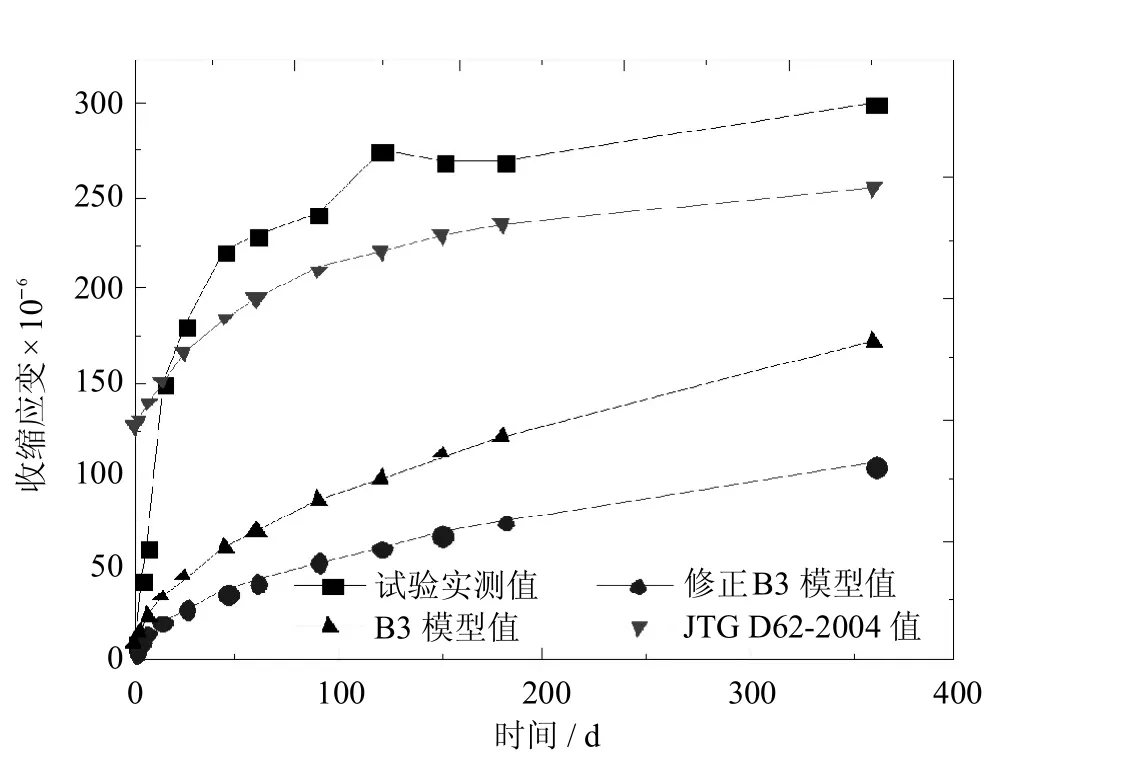
图9 S1试件收缩数据对比Fig.9 Comparison of specimen S1 shrinkage data

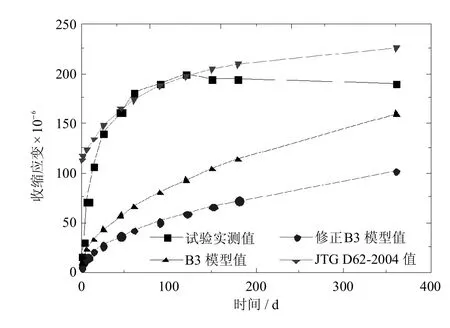
图10 S2试件收缩数据对比Fig.10 Comparison of specimen S2 shrinkage data

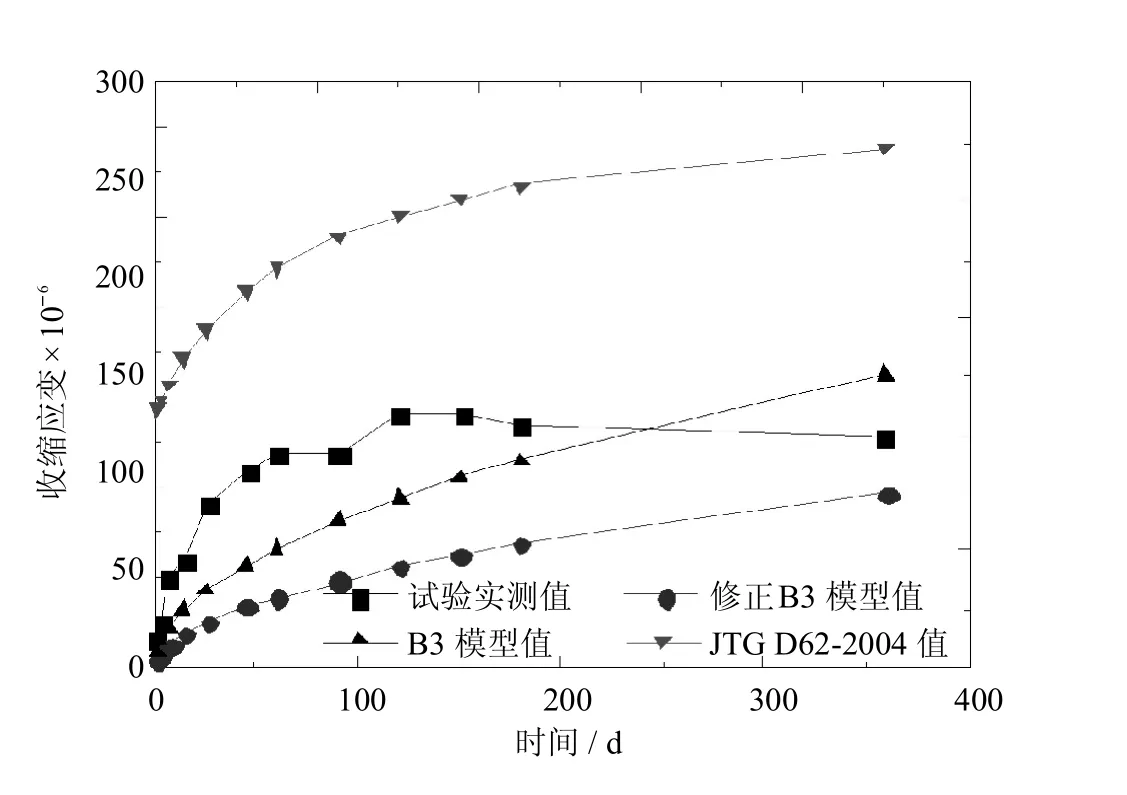
图11 S4试件收缩数据对比Fig.11 Comparison of specimen S4 shrinkage data

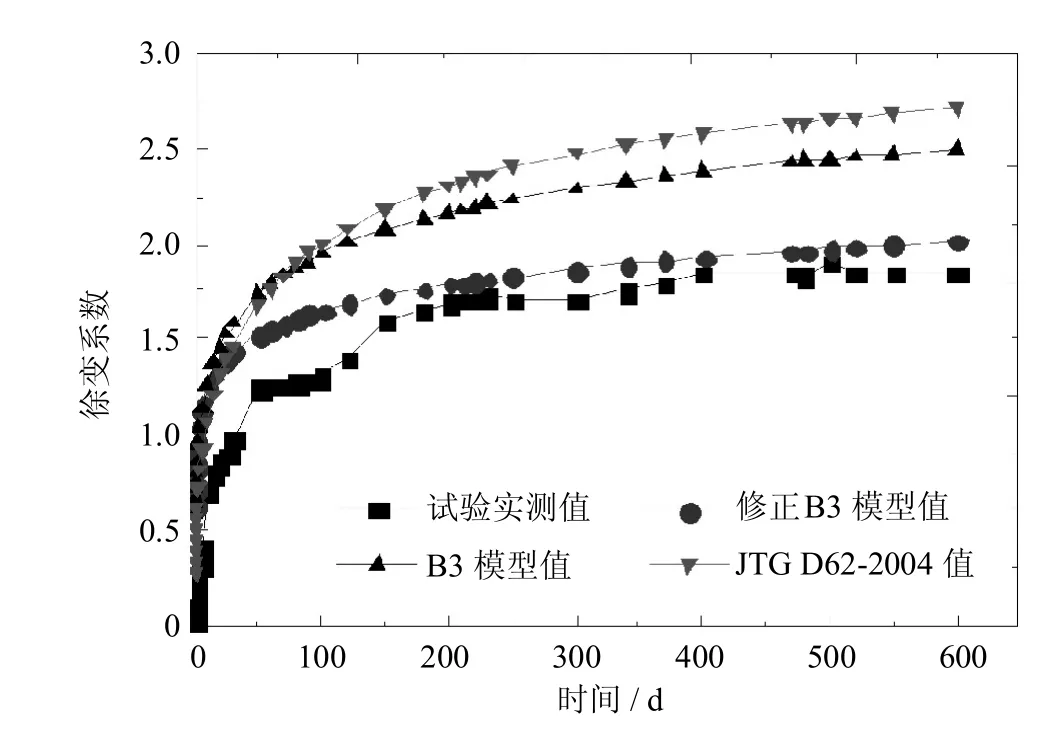
图12 t=3 d徐变数据对比Fig.12 Comparison of thespecimen of t=3 d creep data

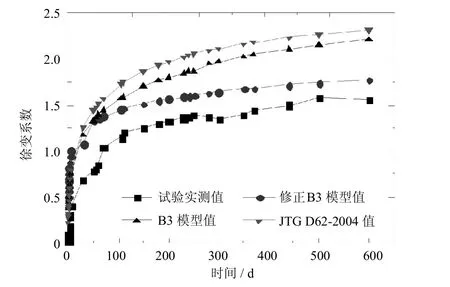
图13 t=7 d徐变数据对比图Fig.13 Comparison of the specimen of t=7 d creep data

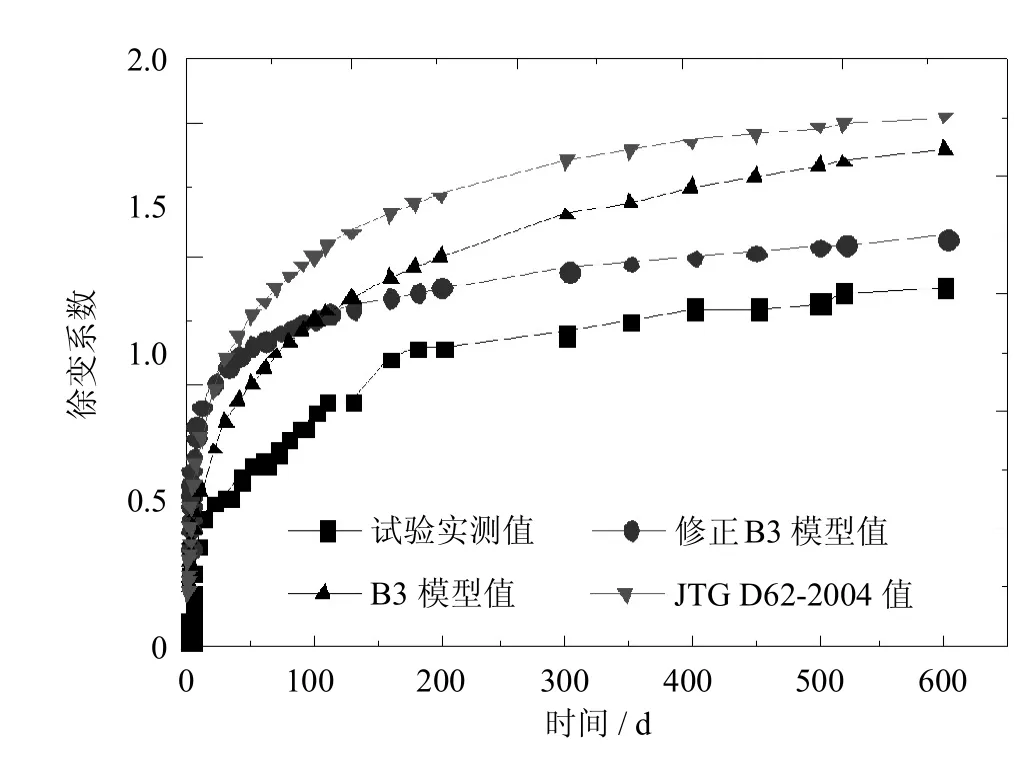
图14 t=14 d徐变数据对比Fig.14 Comparison of the specimen of t=14 d creep data

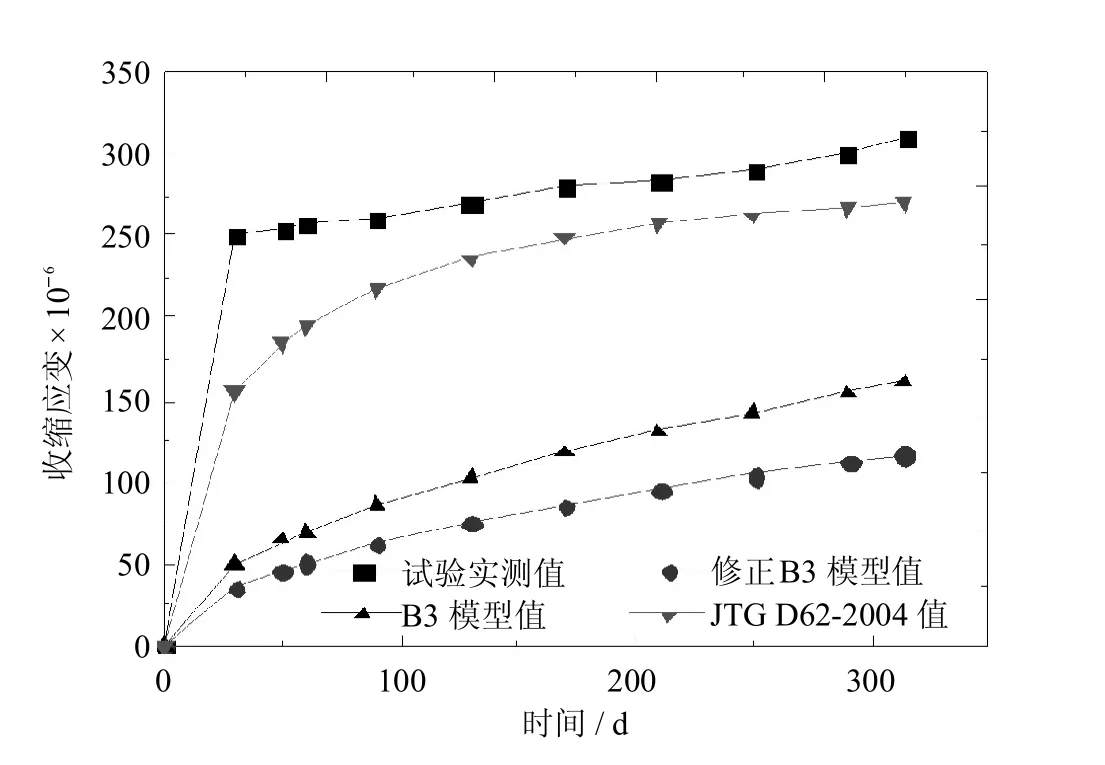
图15 t=7 d，a=100mm收缩试件数据对比Fig.15 Comparison of the specimen of t=7 d, a=100mm shrinkage data

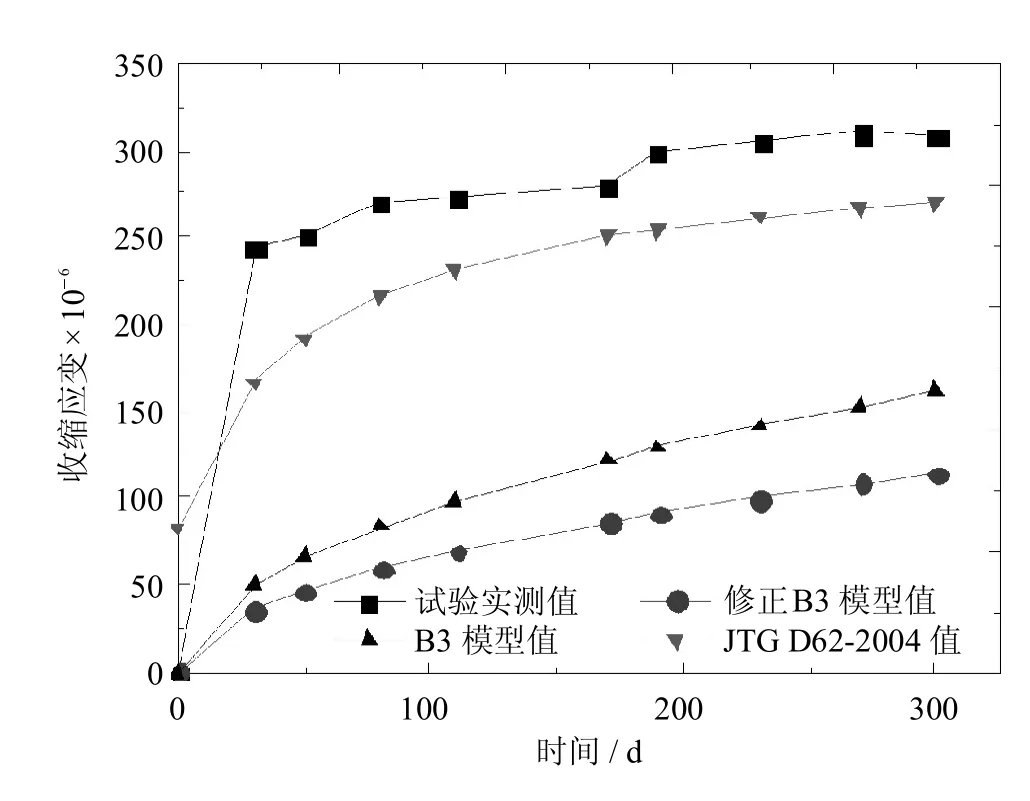
图16 t=14 d，a=100mm收缩试件数据对比Fig.16 Comparison of the specimen of t=14 d, a=100mm shrinkage data

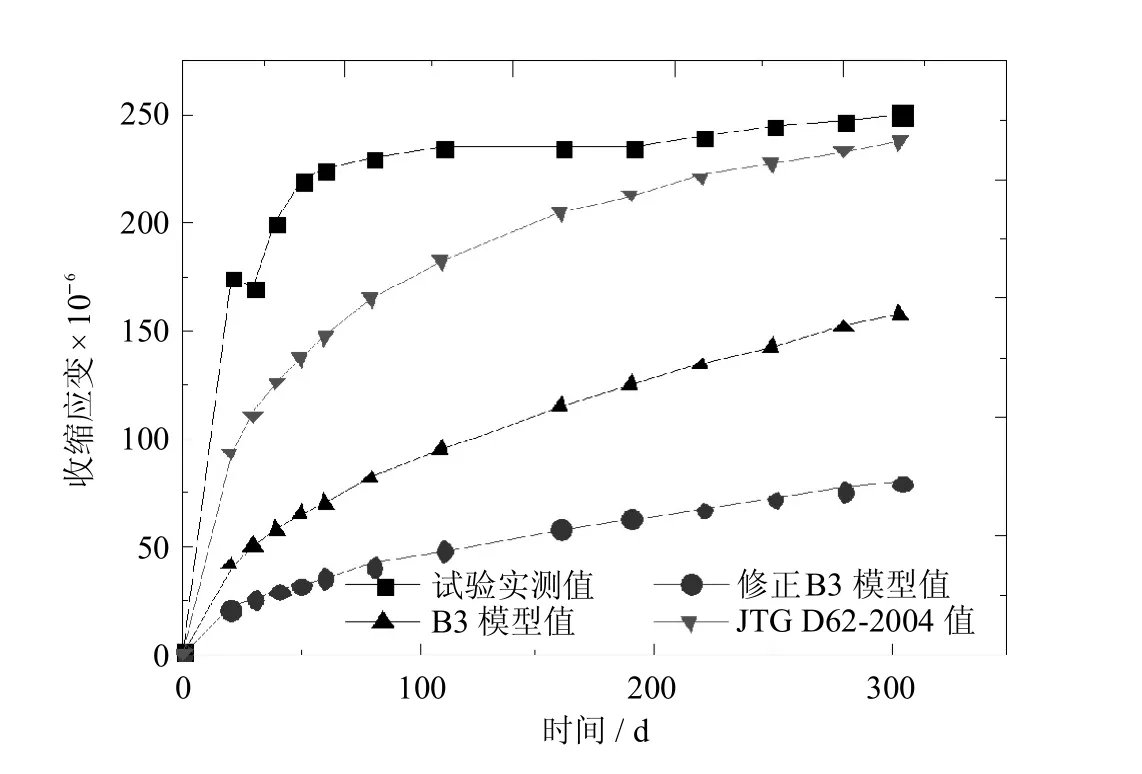
图17 t=7 d，a=150mm收缩试件数据对比Fig.17 Comparison of the specimen of t=7 d, a=150mm shrinkagedata

由图12～图14可见，对于徐变系数而言，该修正公式所算结果与B3公式所算结果趋势一致，但两者数据稍有差别，产生的主要原因是修正模型基于的B3模型基准条件是C40混凝土，而试验为C60混凝土，且影响因素的累计效应使得两者产生偏差．但据图可以得知，该修正公式所算结果与试验实测值更接近，且拟合效果要优于JTG D62-2004模型；由图15～图17可见，对于收缩应变而言，该修正公式所算结果与B3公式所算结果趋势一致，且数值差别不大，但JTG D62-2004模型计算结果与实测值更接近．

5 结论

1）对于徐变而言，影响较大的因素为加载时间、混凝土中水泥含量、混凝土强度等级及养护条件等；对于收缩而言，影响较大的因素为构件体表比、混凝土中含水量、水泥种类、混凝土强度等级及养护方法等．

2）通过延迟构件加载时间、控制混凝土中水泥含量、提高混凝土强度等级及注意混凝土构件的养护等途径可以有效降低混凝土徐变；通过增大构件体表比、减小混凝土中的含水量、使用优质水泥、提高混凝土强度等级及注意混凝土构件的养护等途径可以有效降低混凝土收缩．

3）通过将不同性能的多组混凝土构件收缩徐变试验实测数据与各模型值比较发现，该修正模型与B3模型计算结果趋势一致，数值差别不大，但在公式形式上构造清晰，易于编程，能快捷的应用于工程计算．

4）在无短期试验数据的情况下，计算构件徐变系数时，建议采用此修正模型；计算构件收缩应变时，建议采用JTG D62-2004模型．

[1]项海帆．高等桥梁结构理论[M]．第2版．北京：人民交通出版社，2013．

[2]TJD62-2004，公路钢筋混凝土及预应力混凝土桥涵设计规范[S]．北京：人民交通出版社，2004．

[3]BazantZP，BawejaS．Justification and RefinementofModelB3 forConcreteCreep and Shrinkage[J]．Materialsand Structures，1995，5（28）：488-495．

[4]叶列平，孙海林．HSLWAC梁收缩和徐变预应力损失试验[J]．东南大学学报（自然科学版），2007，37（1）：94-99．

[5]陈露一，欧阳华林．C60低收缩徐变高性能混凝土的配制与试验研究[J]．世界桥梁，2014，42（6）：50-53．

[6]潘钻峰，吕志涛．高强混凝土收缩徐变试验及预测模型研究[J]．公路交通科技，2010，27（12）：10-15．

[7]周氐．现代钢筋混凝土基本理论[M]．上海：上海交通大学出版社，1989．

[8]段明德．《公路钢筋混凝土及预应力混凝土桥涵设计规范》徐变系数的计算和应用[J]．中国公路学报，1998，32（10）：70-76．

[9]杨小兵．混凝土收缩徐变预测模型研究[D]．武汉：武汉大学，2004．

[责任编辑 杨屹]

Modification and verification ofmodel B3 forshrinkage and creep of concrete

QIJinzhen1，ZHU Jinsong1,2

(1.SchoolofCivilEngineering,Tianjin University,Tianjin300072,China;2.Key LaboratoryofCoastCivilStructureSafety,M inistry of Education,Tianjin 300072,China)

Based on the B3modelw ith ahigh degreeof recognition in theworld,amodifiedmodelofshrinkageand creep ofconcreteisgiven.Thishassolved theproblem thatcontainsan integralcoefficientand can notbe calculated continuously. Using themethod of controlling variables,the sensitivity of the factors thataffect the shrinkage and creep of concreteare qualitatively analyzed.In this paper,themodified model is verified by multiple sets of experimental data.From the contrast,we can see thatthe resultofmodified formula isconsistentw ith the trend of B3 formula,and thenumericalvalue has little difference;themodified formula results aremore close to themeasured values,and the fitting effect is better than JTGD62-2004modelwhen itcomes to the creep coefficient.For theshrinkagestrain,the resultsofmodified formula and B3 formula are consistent.And the numericalvalue has little difference.

concrete;shrinkage and creep;B3model;modifiedmodel

TU312

A

1007-2373(2016)03-0100-09

10.14081/j.cnki.hgdxb.2016.03.017

2015-11-12

国家自然科学基金（51178305）；天津市应用基础与前沿技术研究计划（14JCYBJC21500）

齐金振（1991-），男（汉族），硕士生．通讯作者：朱劲松（1975-），男（汉族），教授，博士，博士生导师．