关于并发系统分支互模拟关系发散性保持的研究①

廖文琪, 柳欣欣

1(中国科学院 软件研究所计算机科学国家重点实验室, 北京 100190)2(中国科学院大学, 北京 100190)

关于并发系统分支互模拟关系发散性保持的研究①

廖文琪1,2, 柳欣欣1

1(中国科学院 软件研究所计算机科学国家重点实验室, 北京 100190)2(中国科学院大学, 北京 100190)

带发散性说明的分支互模拟是van Glabbeek和Weijland提出的一个概念, 并被用来定义等价关系≈bΔ. 该等价关系应该是最弱的一个发散性保持的并且满足分支互模拟性质的等价关系. 然而在概念提出时并没有提供这些重要性质的证明, 并且我们认为在原定义的基础上这个证明是不显然的. 本文通过co-induction的手段利用染色迹的概念定义了着色完全迹等价, 并证明该等价关系是最弱的一个保持发散的并且满足分支互模拟性质的等价关系. 然后我们证明了着色完全迹等价关系和是相同的, 因而补充了van Glabbeek和Weijland的工作, 即证明了≈bΔ是最弱的一个保持发散的并且是满足分支互模拟性质的等价关系.

分支互模拟等价关系; 发散性; 发散性保持; co-induction定义; 染色迹

软件系统对社会的各个方面起着重要的作用. 很多软件有着非常复杂的结构. 因而软件的生产需要理论上的支持以构建可靠的软件系统[1]. 通过建立给定程序以及程序的计算环境所组成的软件系统抽象模型和程序的性质规约之间的某种等价关系比如互模拟是验证程序正确性的有效方法[2,3].

并发理论的基本问题是两个并发系统在什么时候可以看作是相等. 在提出通信系统演算(CCS)[4]的时候, Robin Milner就提出了所谓的观察等价, 之后Park在对标号迁移系统的研究中采用co-induction的方式定义了互模拟等价关系[5], Park不但给出了互模拟关系的严格定义, 而且为证明互模拟等价关系提供了重要的方法.

在并发系统中, 发散性是一个重要的性质, 它通常涉及的是一个进程有无穷多个内部动作, 不能同外界环境交互. 对于一个等价关系≡, 如果P和Q具有P≡Q时,P是发散的当且仅当Q也是发散的, 则称≡是发散性保持的[6]. 发散性是对进程内部性质的约束,涉及到程序的终止性和进程的前进属性, 因此利用等价关系验证程序正确性时, 等价关系的发散性保持是非常重要的性质.

互模拟等价关系是一种观察理论, 侧重于系统与外部环境的交互, 着重研究的是可见的外部性质, 而对内部动作进行抽象处理. 经过内部动作抽象出来的互模拟等价关系常常不保持发散性, 需要添加额外的约束. 分支互模拟(branching bisimulation)[7]是由van Glabbeek和Weijlang提出的一种进程等价关系. 研究发现分支互模拟关系不是发散性保持的. 因此van Glabbeek和Weijland对分支互模拟作了额外约束, 提出了带发散性说明的分支互模拟关系(branching bisimulation with explicit divergence)[7]. 然而, 利用该概念在证明相关性质时不够直接, 等价关系传递性上的证明太过复杂[8]. 主要原因是:

① 该概念不能用单个单调函数的不动点来表示;

② 需要对无限运行序列的相关状态的发散性进行分类讨论, 然后归纳证明.

为了解决上述问题, 我们首先使用co-induction思想同时借用染色迹概念定义了着色完全迹等价关系(coloured complete trace equivalence), 该等价关系能通过一个单调函数的不动点刻画, 之后利用刻画函数的最大不动点理论在概念的定义上证明其等价关系和发散性保持性质, 最后我们说明着色完成迹等价和带发散性说明的分支互模拟关系是相同的. 从新概念出发,利用不动点理论大大降低了证明的复杂程度.

1 基本概念和符号说明

文章中主要涉及到如下几个概念: 标号迁移系统(labeled transition systems), 着色(colouring), 带发散性说明的分支互模拟关系(branching bisimulation with explicit divergence). 本文中在证明中对分支互模拟概念没有细节上的涉及而是通过不同进程和系统状态有同一颜色来体现其等价关系, 因此在这里就不给出定义, 后文中作者提出的定义也在后续的证明中给出.我们所有的研究都是在标号迁移系统上进行的, 首先给出标号迁移系统[1]的定义和一些符号说明.

定义 1. 标号迁移系统(labeled transition systems):一个标号迁移系统是一个三元组M=＜S,A, →＞, 其中

①S为状态集合;

②A为标号集合;

③ →⊆S×（A∪τ）×S是一个有标号的迁移关系. 其中τ是内部动作, 通常假设其不在集合A中, →中的一个元素（s,α,t）表示一次迁移, 记为

④M的一个有限运行系列是指由状态和动作交替组成的非空有限迁移系列, 记为ρ=s0α0s1α1Λsn-1αn-1sn, 其中first(ρ)=s0, last(ρ)=sn, length(ρ) =n;

⑤M的一个无限运行系列是指由状态和动作交替组成的非空无限迁移系列, 记为ρ=s0α0s1α1Λ其中first(ρ)=s0.

一般情况下, 我们可以通过连接已有的运行系列,状态和动作形成新的运行系列.

存在多步τ迁移时, 可以通过一些标准符号进行简略表示:s⇒s,表示存在一个以s,s,分别作为起始状态和结束状态的有穷运行系列, 其中所有的动作均为τ.

结束了对标号迁移系统的定义和相关符号的说明之后, 接下来给出van Glabbeek在刻画发散性保持性质中使用到的染色迹概念[8], 从定义着色(Colouring)开始.

定义 2. 着色(Colouring):M=＜S,A, →＞是一个标号迁移系统(LTS),M的着色是一个在状态集合S上的等价关系; 给定一个着色C和一个状态s∈S,s的一个颜色C（s）是一个包含s的等价类. 其中

① 一个C-coloured运行是指由颜色和动作交替组成的一个非空有限系列, 以一种颜色起始, 终止于一种颜色;

② 一个着色C导出一个从M的有限运行系列集合到C-coloured运行系列集合的映射, 记为, 在运行系列长度上的归纳定义如下:

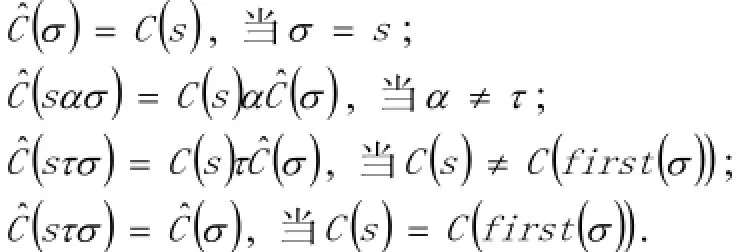
记（σ）为有限运行系列σ的C-coloured运行系列;

③ρ是标号迁移系统M的一个无限运行系列,（ρ）为ρ的所有有限运行前缀的C-coloured运行系列组成的集合, 记为的一个有限运行前缀};

④ 对s∈S, 称s关于着色C发散, 若存在一个以s为起始状态的无限运行系列记为s⇑C; 我们称ρ是一个发散运行系列, 当ρ中所有的动作均为τ且ρ所有的状态均为颜色C（s）时.

引理 1.M=＜S,A, →＞是一个标号迁移系统(LTS),C为M的一个着色,ρ是一个有穷运行.

① 对s∈S, 若（ρ）=C（s）, 则ρ中的所有动作均为τ且ρ所有状态的颜色为C（s）;

② 对t,t,∈S, 若则存在且时有时有

证明: 使用归纳法证明, 在ρ长度上进行归纳证明可完成①的证明. 在证明①为真的基础上,ρ长度上进行归纳证明可得到②.

在完成对基本概念的准备和记号的说明后, 我们给出van Glabbeek提出的带发散性说明的分支互模拟关系[7].

定义 3. 带发散性说明的分支互模拟关系(branching bisimultiaon with explicit divergence):M=＜S,A, →＞是一个标号迁移系统(LTS),C为M的一个着色.

① 着色C是一致的(consistent), 如果对任意C（s）=C（t）, 其中s,t∈S, 若存在一个以s为起始的有穷运行系列σ, 则必然存在一个以t为起始的有穷运行ρ且有

② 着色C是发散性保持的(divergence preserving), 如果对任意C（s）=C（t）, 其中s,t∈S, 若s⇑C, 则t⇑C.

对s,t∈S, 如果存在一个一致的且是发散性保持的着色C, 使得C（s）=C（t）, 则称s和t是带发散性说明的分支互模拟等价关系, 记为

我们希望定义4给出的关系是一个等价关系, 并且具有分支互模拟性质, 并且是保持发散性, 并且是具备所有以上性质的最弱的那个等价关系. 但在概念提出时[7]并没有提供这些事实的证明, 后续的研究[8]也只有部分证明(证明了它是一种等价关系). 在下面章节中, 我们将定义一个等价关系, 并且证明这个等价关系具有上述性质, 最后证明这个等价关系和定义4给出的是相同的.

2 概念的提出及性质证明

2.1 染色迹完全等价

本节我们将定义一个新的等价关系, 该等价关系利用染色迹(colour trace)概念使用co-induction的方式完成对一致性和发散性保持的刻画, 定义着色完全迹等价关系, 并证明这个关系是最弱的同时发散性保持和分支互模拟性质的等价关系.

定义 4. 着色完全迹等价关系(coloured complete trace equivalence):M=＜S,A, →＞是一个标号迁移系统(LTS),C为M的一个着色.C是完全迹一致的(complete trace consistent), 如果对任意C（s）=C（t）, 其中s,t∈S, 蕴含着

① 若存在一个以s为起始的有穷运行系列σ, 则必然存在一个以t为起始的有穷运行ρ且有

② 若存在一个以s为起始的无穷运行系列σ, 则必然存在一个以t为起始的无穷运行ρ且有

对s,t∈S, 如存在一个完全迹一致的着色C, 使得C（s）=C（t）, 则称s和t是着色完全迹等价关系, 记为s≈cct.

2.2 ≈cc的性质说明

为帮助完成对≈cc性质的研究, 引入函数, 其定义如下:

定义 5.M=＜S,A, →＞是一个标号迁移系统(LTS),C为M的一个着色. 函数(C)是定义在状态集合S上的二元关系, 对当且仅当满足下列两个性质:

引理 2.

②C是完全迹一致的当且仅当{（s,t）|s,t∈S,C（s）=C（t）}⊆（C）成立

证明: 引理中①和②的证明可以在定义4和定义5中直接推导获得. ③的证明可以转化为证明: 存在在状态集合S上的两个等价关系≡1, ≡2且有≡1⊆≡2, 则有(≡1)⊆(≡2). 该单调性的证明从函数定义出发不难获得.

定理 1.M=＜S,A, →＞是一个标号迁移系统(LTS),则≈cc是在状态集合S上的等价关系, 同时≈cc是一个完全迹一致的着色并且是M中完全迹一致着色刻画的等价关系中最粗粒度的那个.

证明: 令｛≡i｝i∈I为在状态集合S上的等价关系的集合, 根据集合知识我们可以得到下面几个事实:

① ∩｛≡i|i∈I｝是在集合S上的等价关系;

② 对所有i∈I, ∩｛≡i|i∈I｝⊆≡i均成立;

③ 如果≡是状态集合S上的等价关系且对所有i∈I, 均有≡⊆≡i, 则≡⊆∩｛≡i|i∈I｝;

⑥ 如果≡是在状态集合S上的等价关系并且对所有i∈I均有≡i⊆≡, 则有

令ε为状态集合S上的等价关系的集合, 则由上述事实可知ε的任意子集在关系⊆中既有最大下确界也有最小上确界, 因此（ε,⊆）是一个完全格. 又由引理2可知函数是在该完全格中的单调函数, 则根据Knaster-Tarski不动点理论[9]可知函数有最大不动点FIX（）∈ε, 该不动点有如下性质:

② 对任意≡∈ε, 当≡⊆(≡)时, 有

综上所得定理1得证.

定理1的证明应用到了Knaster-Tarski不动点理论,证明了≈cc是一个单调函数刻画的最大不动点. 这使得定理1的证明清晰而且规整. 相比较而言,因为不能由单个单调函数的最大不动点进行刻画获得, 使得等价关系的证明不明显, 性质的说明也不充分. 接下来通过一个例子来对刻画的函数的单调性加以说明.

同样, 我们需引入一个在ε上的函数℘, 定义如下:

≡是状态集合S上的一个二元等价关系, （s,t）∈℘(≡)当且仅当对（s,t）∈S×S, 满足下面两个条件:

②s⇑C当且仅当t⇑C.

文献[8]对≈bΔ的性质进行了说明, 并证明了其为一个等价性关系, 且具有发散性保持的性质, 这些结论不是通过对函数℘应用Knaster-Tarski定理得到的,因为函数℘不具有单调性, 下面我们给出一个反例(如图1所示) .

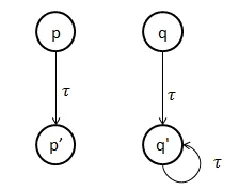
图1 函数℘单调性反例

≡1和≡2是定义在状态集合S上的等价关系且有≡1⊆≡2, 其中有p≡1q,p,≡1q,, 且p和p,,q和q,不具有关系≡1;p,q,p,,q,之间均有关系≡2; 根据定义可知p和q在≡1中均不发散, 有（p,q）∈℘(≡1);但p在≡2中不发散,q在≡2中发散, 有（p,q）∉℘(≡2), 故℘不具有单调性.

定理 2. 如果二元等价关系≡是完全迹一致的着色, 则≡是发散性保持的.证明: ≡是一个完全迹一致的着色, 则可假设s≡t且有s⇑C; 根据发散的定义, 则存在一个以s为起始的无限运行系列σ且又≡是一个完全迹一致的着色, 故存在一个以t为起始的无限运行系列ρ且又因为s≡t, 所以进而得到即t⇑C; 所以≡是发散性保持的.

推论 1. ≈cc是发散性保持的.

证明: 由定理1可知≈cc是一个完全迹一致的着色, 结合定理2可知≈cc是发散性保持的.

至此, 我们对≈cc的性质进行了全面的说明, 证明了≈cc是一个等价关系, 当着色时使用的是分支互模拟关系时, ≈cc是分支互模拟等价关系, 具有发散性保持的特性, 同时也是具备所有以上性质的最弱的那个等价关系.

2.3 ≈cc和关系

由上节对≈cc性质的描述我们知道, ≈cc是最粗粒度的具有发散性保持的分支互模拟等价关系.同样是最弱的带发散性保持的分支互模拟等价关系[7-8]. 那么和≈cc之间的有什么关系, 本节将对其进行完整的阐述.

定理 3.M=＜S,A, →＞是一个标号迁移系统(LTS),≡是在状态集合S上的二元等价关系, 则≡⊆(≡)当且仅当≡是一致的且是发散性保持的.

证明:

上述定理告诉我们定义3和定义4中获得的两个关系的条件是相同的, 得到的等价应该也是相同的,即将在定理4中给出完善的证明. 这不禁让人疑问: 两个定义给定的条件是可以互推得到的, 关系也是相同的, 为什么刻画该关系的函数会在单调性上有不同的表现. 比较两个定义的条件发现, 两种定义都分为两个部分, 第一部分是对有限运行系列的一致性的要求, 两种定义此部分完全相同, 区别在第二部分对无限系列的发散性保持上的约束. 定义3只对无限系列相关状态的发散性保持做了要求, 对其有限子系列的一致性并没有说明, 而定义4对无穷运行系列中的相关状态的发散性和一致性都给出了明确的说明. 从这个角度上看定义4的条件比定义3更强, 这个说法没有问题, 但事实是对发散性保持的说明本身其实蕴含着从相关状态起始的无限系列的有限子系列具有一致性, 但需要进一步的说明. 定义4不能使用单个单调函数进行刻画获得最大不动点性质, 但使用两个函数可以完成对其该性质的阐述.

定理 4.M=＜S,A, →＞是一个标号迁移系统(LTS).则

② ≈bΔ是在状态集合S上的二元等价关系, 同时具有一致性和发散性保持特性, 并且是标号迁移系统M中最弱的带发散性保持的等价关系.

证明:

① 由定理2可知≈cc是发散性保持的, 并且是一致的, 根据定义3, 有任意s,t∈S, 如果则存在一个等价关系≡, ≡是一致的并且是发散性保持的且有s≡t, 由定理3可知≡⊆(≡), 运用引理2可知≡是完全迹一致的, 故s≈cct, 即综上

② 由定理1可知≈cc是在状态集合S上的等价关系, 由于所以也是在状态集合S上的等价关系, 同时在定理8中我们对≈cc的最弱等价性进行了证明, 同样也可以迁移到上.

3 结语

分支互模拟关系发散性保持的研究对并发系统理论发展和并发程序的验证具有重要的意义. 尽管van Glabbeek等提出了带发散性说明的分支互模拟概念并对其性质进行了一定的说明, 但我们提出了着色完全迹等价关系对分支互模拟关系的发散性保持问题进行了研究, 从另一个角度证明了带发散性说明的分支互模拟概念的性质, 完善了其工作. 本文的研究有以下贡献和创新性:

① 使用co-induction方式定义了着色完全迹等价关系, 并证明了其为最弱的发散性保持的分支互模拟等价关系.

② 对刻画带发散性说明的分支互模拟关系的函数的单调性进行了说明.

③ 建立了着色完全迹等价关系和带发散性说明的分支互模拟等价关系之间的联系, 完善带发散性说明的分支互模拟关系的研究工作.

④ 研究了发散性保持的分支互模拟等价关系,为应用该关系验证程序的正确性提供帮助.

1 张文辉.软件系统行为与程序正确性.http://lcs.ios.ac. cn/～zwh/pv/pv13.pdf.

2 Liang H, Feng X, Fu M. A rely-guarantee-based simulation for verifying concurrent program transformations. ACM SIGPLAN Notices, ACM, 2012, 47(1): 455–468.

3 Liang H, Hoffmann J, Feng X, et al. Characterizing progress properties of concurrent objects via contextual refinements . CONCUR 2013–Concurrency Theory. Springer Berlin Heidelberg, 2013: 227–241.

4 Milner R. Communication and Concurrency. Prentice-Hall, Inc., 1989.

5 Park D. Concurrency and automata on infinite sequences. Gi-Conference on Theoretical Computer Science. Springer-Verlag. 1981. 167–183.

6 何超栋.CCS的基本问题研究[博士学位论文].上海:上海交通大学,2011.

7 Van Glabbeek R, Weijland W. Branching time and abstraction in bisimulation semantics. Journal of the ACM, 1996.

8 Van Glabbeek R, Luttik B, Trcka N. Branching bisimilarity with explicit divergence. Fundamenta Informaticae, 2009, 93(4): 371–392.

9 Paulson LC. A Fixedpoint Approach to Implementing (co) Inductive Definitions. Springer Berlin Heidelberg, 1994.

Branching Bisimulation with Explicit Divergence in Concurrent Systems

LIAO Wen-Qi1,2, LIU Xin-Xin112
(State Key Laboratory of Computer Science Institute of Software, Chinese Academy of Sciences, Beijing 100190, China) (University of Chinese Academy of Sciences, Beijing 100190, China)

The notion of branching bisimulation with explicit divergence was introduced by van Glabbeek and Weijland. It is used to define an equivalence relation, which means to be the weakest equivalence with the property of branching bisimulation and divergence preservation. However, in that paper it only claims that ≈bΔis an equivalence with such properties without proofs, and as it turns out that the proving is not obvious. In this paper we introduce an equivalence relation called coloured complete trace equivalence, and prove that it is the weakest equivalence which has the property of branching bisimulation equivalence and is also divergence preserving. We then prove that the coloured complete trace equivalence coincides with, thus supplementing the work of van Glabbeek and Weijland.

branching bisimulation; divergence; divergence preserving; co-induction; colour trace

国家自然科学基金(NSFC-91418204)

2016-03-21;收到修改稿时间:2016-04-05

10.15888/j.cnki.csa.005431