GROMACS软件并行计算性能分析①
张宝花, 徐 顺
(中国科学院计算机网络信息中心 超级计算中心, 北京 100190)
GROMACS软件并行计算性能分析①
张宝花, 徐 顺
(中国科学院计算机网络信息中心 超级计算中心, 北京 100190)
分子动力学模拟是对微观分子原子体系在时间与空间上的运动模拟, 是从微观本质上认识体系宏观性质的有力方法. 针对如何提升分子动力学并行模拟性能的问题, 本文以著名软件GROMACS为例, 分析其在分子动力学模拟并行计算方面的实现策略, 结合分子动力学模拟关键原理与测试实例, 提出MPI+OpenMP并行环境下计算性能的优化策略, 为并行计算环境下实现分子动力学模拟的最优化计算性能提供理论和实践参考. 对GPU异构并行环境下如何进行MPI、OpenMP、GPU搭配选择以达到性能最优, 本文亦给出了一定的理论和实例参考.
分子动力学模拟; GROMACS; 并行计算
2013年的诺贝尔化学奖授予了Martin Karplus、Michael Levitt和Arieh Warshel三位理论化学家, 以肯定他们在 “开发多尺度复杂化学系统模型”方面所做的贡献. 他们发展了大量分子动力学(MD: Molecular Dynamic)模拟基本理论和计算方法, 实现了更好地通过微观相互作用研究体系的宏观性质. 这一类强有力的计算化学方法渗透于迅速发展的分子生物学、生物信息学和生物物理学等前沿交叉学科, 同时逐渐形成一系列典型计算与模拟软件, 包括: GROMACS、NAMD、LAMMPS、AMBER、CHARMM等[1-5]. 高性能并行计算技术应用于分子动力学模拟, 使得体系模拟能够在更大空间尺度和时间尺度上进行. 比如GROMACS软件的基础框架设计就立足在高性能计算环境.
GROMACS是开源分子动力学通用软件包, 面向百万级甚至亿万级粒子体系的模拟[1]. 它具有多种并行模式: MPI、MPI+OpenMP、Thread-MPI, 还支持GPU等加速器的应用. GROMACS 4.6以后针对GPU kernel进行了重新设计, CPU和GPU的协调工作方式对计算性能变得更为敏感[6]. 针对MD模拟中的力场计算密集型任务, 它采用区域分解技术和动态负载均衡技术,并且计算长程作用力的任务(PME算法)能分类出独立进程负责, 来加速优化计算; 对于大规模粒子体系在并行计算时实行主区域分解技术(DD: Domain Decomposition)[7], Domain区域内的计算任务会映射到一个PP rank (Particle-Particle (PP) interaction MPI rank)上面. 在并行规模较大时, 还会将PME计算分配独立的ranks以减少rank间的通讯量来提高并行计算效率[8]. GROMACS虽然能自动调节rank间的计算负载, 但要达到最佳计算性能还很困难.
GROMACS的计算性能除了硬件影响外, 还有安装编译方式和并行计算策略选择方式的影响, 在硬性约束固定和软件安装编译优化之后, 此时并行计算策略的选择对运行速度影响最为显著. 并行策略方面可调节的方式有: 进程并行数、节点划分、区域分解、作用力计算相关的PME/PP任务分配和GPU/CPU协调工作等. 这些是提升分子动力学模拟并行计算性能的关键因素, 对于GROMACS程序的终端用户意义重大.准确高效地使用软件, 不仅能够节省时间, 更快获取模拟计算结果加快科研进度, 而且由于硬件设备的高效使用能够大幅节省计算成本. 但现实是: 软件程序对于大多用户来说仍然是个黑盒子, 不可避免地存在使用效率上的陷阱. 比如选择何种并行模式? 如何合理分配MPI+OpenMP? 如何有效使用GPU加速卡能够达到计算绝对性能最优, 同时不会造成硬件资源的隐形浪费? 这些都是用户非常关注且迷惑的问题. 因此有必要对GROMACS的并行计算性能进行分析研究.
本文分析GROMACS软件在分子动力学模拟并行计算方面的实现策略, 先阐述MD模拟中涉及计算方法的并行化设计与实现关键问题, 在原理和算法分析之后, 以最优并行计算为目标, 提出CPU并行中如何调节并行计算优化策略方案. 文中还讨论了异构并行环境下GROMACS并行计算的实现原理, 并对GPU异构加速时计算性能调节给出了有益参考.
1 GROMACS并行计算优化策略
GROMACS采用了MD模拟中的区域分解并行设计方式, 以MPI为主要的并行环境, 加入OpenMP和CUDA-GPU实现热点并行加速计算. 为获得最佳计算性能, 常需要综合考虑不同的并行组合方式. 根据GROMACS软件并行设计方式以及影响并行计算性能的分子作用力计算的问题, 针对 MPI搭配OpenMP线程并行方式我们提出相应的优化策略方案, 并对存在GPU异构加速情况下并行优化作探索.
1.1 非成键力计算与PME计算性能优化
优化GROMACS MD模拟关键在于优化分子作用力的计算. 分子作用力大致分为: 成键力和非成键力,非成键力有范德华力和静电场力等形式. 直接计算非成键力的复杂度为O(N2), N为体系的粒子数, 这也使得它成为并行优化的关键问题. GROMACS采用PME(Particle Mesh Ewald, 包括LJ-PME)[9]算法来加速非成键力的计算, Ewald算法是PME的基础, 在粒子数为N的周期性边界体系中, 静电势能U可以表达为

其中静电常量k是关于介电常数ε的量k=1/4πε, 而rij,n=|ri-rj+n|表示电荷粒子i和j在跨越镜像格矢n间的真实距离, 镜像格矢n=(nx,nv,nz), 添加*号表示当在原像中即n=(0,0,0)时排除i=j的情况. Ewald方法将慢收敛的式(1)转换为两个快收敛项和一个常数项

其中



实空间(direct space)表达式Udir中erfc为互补误差函数, 倒易空间(reciprocal space)表达式Urec中V为模拟盒子的体积, 系数β同时出现在三项中用于调节它们计算的相对权重. 比如将β系数取较大值,Udir会相对于r收敛很快, 因此可以采用截断r来减少其计算量, 而不影响计算精度. 实际上Ewald方法的计算复杂度仍然为O(N2), 而PME在计算Urec时引入了快速傅里叶变换操作加快了计算, 同时采用大β系数加快Udir收敛便于计算中使用截断操作, 最终PME总体上计算复杂度达到了O(Nlog(N)), 在大体系模拟中加速性能显著.
非成键力按照作用范围分为短程和长程非成键力.短程非成键力(如静电场计算Udir)在实空间计算, 长程非成键力(如静电场计算Urec)常变换到倒易空间计算. PME算法是用于加速长程非成键力计算的一种常用方法, 其它类似算法还有Reaction Field方法等.

图1 GROMACS中分子间作用力的分类
GROMACS中计算作用力主要分为两大类(见图1): PP rank, 包括成键相互作用和短程非键相互作用(对应于公式(2)中的Udir和U0), PP作用力计算的距离范围阈值为rc(=max(rvdw,rcoulomb,rlist))[10]; PME rank, 包括长程非键相互作用(PME算法, 包括LJ-PME, 对应于公式2中的Urec). PME rank通过从PP实空间处理器获取电荷、坐标等信息, 在倒易空间中进行栅格化和3D FFT及反演计算, 最后将计算得到的力、能量及维里等返回实空间处理[11]. PME和PP rank的任务多寡与负载均衡在并行模拟优化时需着重考虑.
GROMACS使用纯CPU计算时, PP和PME的计算可以在同一个rank上, 也可以将PME计算部分开辟一些独立的ranks处理. 前一种方式由于PME计算需要大量的全局通讯, 随着并行规模的增加, 通讯复杂度会大大增加, 因此只针对小并行规模模拟. 后一种方式可以降低通讯复杂度, 故适合大规模并行模拟.例如使用64个ranks时, 其中分配16个PME ranks, 其余48个为PP ranks, PP和PME ranks仅在需要的时候通讯, 大大降低了通讯的复杂度(PME ranks减少4倍,通讯量就会减少16倍), 尤其是在大规模并行时, 这种方法往往能大幅提高计算效率. GROMACS在12 ranks以上并行时, 会自动进行PME 独立进程的划分. 在实际模拟计算中, 还可以使用tune_pme (GROMACS 5.0版本以上)小工具来测算最佳的PME ranks和3D-FFT倒易空间三维网格格点数[12].
GROMACS程序实现了动态负载均衡, 通过在一定范围内调节截断半径以及PME格点数及格点间距离来调节成键和非成键相互作用的计算任务来实现.但这种调节必须建立在对体系充分分析并设定合理参数的前提下和对硬件合理分配的基础上进行, 否则仍然会有大量负载不均衡的现象发生. GROMACS程序计算时, 由负载均衡导致的性能损失达到5%或以上时, 默认会自动开启动态负载均衡.
1.2 OpenMP线程计算加速
在CPU节点内并行时, GROMACS可以使用两种并行方式: 标准MPI方式和Thread-MPI并行方式. Thread-MPI并行方式是通过多线程机制模拟标准MPI方式实现的, 只限于节点内应用, 节点间并行模拟仍以标准MPI并行为主, 通过MPI通讯完成. 每一个MPI rank中, 可以开启多个OpenMP线程加速. 需要注意的是: 在一定的可用核数时, 开启OpenMP多线程并行, 由于硬件型号配置等原因, 计算速度不一定会提高[13].
1.3 GPU异构计算加速
GROMACS 使用GPU加速时(目前只支持Verlet方法计算)[14], 如图2[6]所示, 在每一步的计算中, 短程非键相互作用计算会加载到一个或多个GPU卡上. CPU同时在处理成键相互作用和长程非键相互作用(PME, 包括LJ-PME), 这部分计算可以使用OpenMP线程加速计算[15]. 在每步模拟中, GPU端接收CPU端传输的邻接列表、坐标和电荷等信息. GPU在计算短程非键相互作用时, 当有多个domain会分为local和nonlocal两个stream处理, 得到短程非键计算力后再返回CPU端进行其他计算处理, 每隔10-50步由CPU端进行邻接列表的更新. 因此, CPU和GPU之间的负载均衡对程序性能有很大的影响. 如果CPU和GPU任务分配不均, 就会造成一方超负荷运转状态, 而另一方一直在空闲等待状态, 造成硬件资源的隐形消耗.而影响这种负载均衡的因素有三: 一是CPU和GPU硬件的绝对计算能力; 二是CPU和GPU的使用搭配,即CPU/GPU 比例; 三是计算体系的特征.
在实际计算中, GPU异构最佳并行模式与不同的硬件特征和运行体系相关. 例如对于一个非成键相互作用力计算量很大的体系, 假如配备的GPU性能非常强的话, 可以使用较少的CPU配备较多的GPU来达到这一目的, 但如果其他的CPU核心不能被其它任务所合理利用的话, 这样势必会造成硬件资源的闲置与浪费[16]. 因此, 在运行一个较大较长时间任务的时候, 应该先做一个小的测试来确定最佳的计算配置.
GROMACS的非成键相互作用力有三种并行计算方式, 如表1分别可以用-nb gpu/cpu/gpu_cpu选项指定,它们在计算非键相互作用力的方面各有侧重. 使用哪一种方式计算取决于硬件特征和体系的计算特性.

图2 GROMACS中GPU与CPU协调工作机制

表1 GROMACS计算相互作用力的三种并行计算类型
本文提出了CPU和GPU异构环境下的并行计算优化策略:
1) 使用CPU并行环境模拟时, 我们将考虑影响性能的两类主要因素: PP rank间任务负载不均衡对性能的影响; PME独立rank对性能的影响. 并针对具体体系测试结果, 总结性给出计算性能高低判据和并行优化策略方案.
2) 使用GPU异构并行环境模拟时, 我们将考虑影响性能的两类主要因素: CPU/GPU配比, 通过测试找到最佳搭配比, 使资源利用和计算性能最大化; CPU端使用MPI进程和OpenMP线程加速, 通过测试找出合适的进程与线程分配, 为GPU异构并行环境下计算性能最大化提供实践经验参考.
2 实验设计
2.1 运行环境
在中国科学院“元”超级计算机上安装编译GROMACS 5.1单精度浮点MPI版本, 并支持GPU加速. 采用了Intel C/C++ 2013_sp1.0.080版本编译器, Intel MPI 4.1.3并行库(支持了OpenMP线程并行), 链接了MKL高性能并行函数库和fftw3.3.4函数库, 采用了CUDA 6.0.37编译器, 并针对AVX_256指令集进行了优化.
2.2 模拟体系
我们选择了两个具有代表性的生物体系: 一个为均相蛋白体系3MGO(抗原表位多肽与人白细胞抗原复合物)[17], 另一个为膜蛋白体系DPPC(胆固醇-磷脂膜蛋白)[18], 两个体系结构见图3所示, 为突出计算核心部分已隐藏水分子.

图3 3MGO(上)和DPPC(下)体系结构图
表2显示了3MGO和DPPC体系的模拟参数. 为了消除初始态对计算速度的影响, 我们先对体系进行一段MD平衡模拟, 选择分子动力学统计平衡后的体系态作为我们算例测试的初始态.
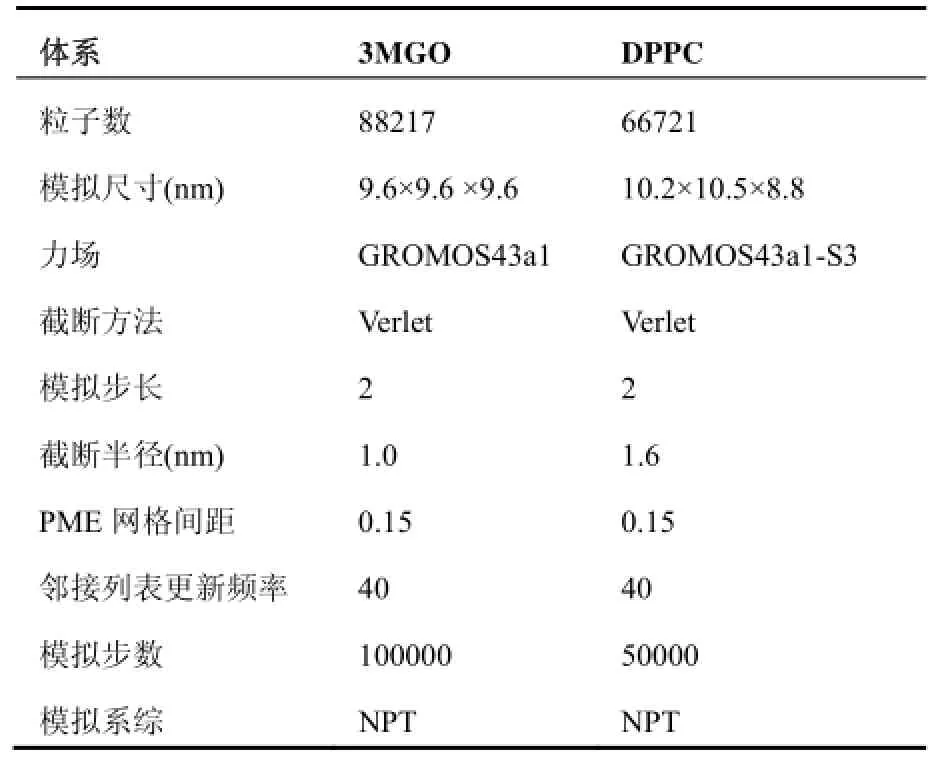
表2 3MGO和DPPC体系模拟参数表
当使用Verlet截断方法计算时, 可以充分利用SSE、AVX 或CUDA, 且PP和PME rank都可以使用OpenMP线程加速. 当使用group截断方法时, 只有PME rank可以使用OpenMP加速, 相对Verlet截断方式并行计算程度低, 且在非键力计算时会出现能量漂移, 故这种情况本文暂不考虑[10].
2.3 并行计算方式
我们首先考虑纯CPU并行计算, 先考虑节点内MPI+OpenMP如何搭配绝对性能最好, 之后对跨节点并行进行性能分析, 并给出性能影响因素和调优方向.加入GPU加速卡后, 首先测试验证节点内CPU/GPU最佳配比, 之后再多节点时考虑MPI+OpenMP+GPU异构的并行性能情况.
在大规模并行计算时, 我们首先采用程序自动评估PME独立进程, 根据性能表现决定是否有必要手动调节PME独立进程. 在运行时, 动态负载均衡默认打开, 可以调节PP任务间和PP/PME任务负载均衡.
“元”超级计算机CPU节点为双路10核CPU, 共20个逻辑核心, 本文不考虑超线程情况, 因为这意味着两个线程要共享一个单浮点数单元, 较大规模并行时性能并没有带来提升. 为方便表述, 在下文中, 我们均用Nrank表示MPI rank数量, Nth表示开启的OpenMP线程数, Npme和Npp表示使用的PME和PP的rank数.
在本测试中, 由于长程非键力计算量较大, 而2块GPU的计算性能相对20 CPU强, 当并行选项为“gpu_cpu”的情况时, 一部分CPU会模拟GPU的计算行为, 计算结果不甚理想. 因此我们仅考虑并行选项“-nb”为CPU和GPU的情况.
我们关注计算性能ns/day的变化, 每组数据都平行进行了至少3次测试取平均值, 以消除系统运行中网络、内存及I/O等繁忙造成的不稳定因素影响.
3 结果与讨论
3.1 仅CPU并行方式
3MGO和DPPC体系节点内并行性能测试表明,当用满一个节点的所有逻辑核心数20(即Nth×Nrank=20)时, 获得的ns/day数值最高, 性能最好.因此, 在接下来的测试中选择总的模拟核心数均为20n(n为节点数).
我们将从PP任务负载不均衡性和PP/PME任务比两个方面来衡量计算性能是否优良. PP任务负载不均衡率包括平均负载不均衡率(Avg. imb%)与每步力计算的不均衡率(Load imb%), 在模拟中会通过改变DD cell的尺寸来调节PP rank的负载, 还会受到体系各项异性的影响. 一般认为这两个值越小越好, 在本测试中认为小于5%即为相对均衡(小规模并行时小于3%). PME/PP比值反映了PME和PP rank的任务分配是否均衡, 理想值为1, 即PME和PP rank的任务分配是完全均衡的. 在实际中, 由于网络通讯等原因,实现PP-PME负载完全平衡几乎是不可能的. 在本测试中认为小于此值在0.8-1.2之间相对均衡.



在较小并行规模时, PP rank间任务负载不均衡是导致性能损失的主要原因.
如图4, 当计算节点为1时, 我们分别取Nrank为1、2、10、20, Nth为20/Nrank. 测试表明, 对于3MGO和DPPC体系, Avg. imb%与Load imb%均为1.2%以下,即每个rank的PP计算任务和每计算步所有力的计算都是相对均衡的. 由ns/day数值来看, 选取较大的Nrank数, 更有利于绝对性能提升. 如3MGO体系: 当Nrank为10和20时, ns/day分别为14.8和14.5. 而Nrank为1和2时, ns/day分别为13.8和13.5. DPPC体系结果相似.
当并行规模扩展到2个节点时, Nrank分别取2、4、20、40, 相应的Nth为 20、10、2、1. 如图5所示, 2个节点计算结果与1个节点相一致, 当Nrank>Nth时, 绝对性能更优.

图4 3MGO和DPPC体系在1个节点时的计算结果
值得注意的是, 当Nrank=4时, PP任务负载不均衡率导致的Avg. imb%较高, 由此造成了部分性能损失(DPPC体系为4, 3MGO为2.9), 这时如果我们调整Nrank与Nth的相对数值, PP任务负载不均衡现象就会得到改善, 计算性能将会得到提升. 如DPPC体系, 我们取Nrank为8, Nth为5时, Avg. imb%降低到了1.9%, 计算绝对性能提升了12%. 对于3MGO体系, 调节Nrank数为8后, 计算性能提升了6.4%.

图5 3MGO和DPPC体系在2个节点时的计算结果
较大并行规模下, 除PP任务负载不均衡外, PP/PME的任务分配不均是导致性能损失的主要原因.

图6 3MGO体系和DPPC体系在5个节点内计算结果
如图6所示, 当并行规模达到5个节点时, Nrank分别取5、10、50和100, Nth分别为20、10、2和1, Nrank>=20时有独立PME rank分配. 在较大并行规模下, PME/PP任务分配不均是导致并行性能损失的主要原因. 例如3MGO体系, 当Nrank=50时, GROMCAS核心程序mdrun自动估算的Npme=15, PME/PP比为1.37, 这说明PME的任务负载比PP rank多出37%, 绝对性能为48.3 ns/day. 当调整Npme=20时, PME/PP比为1.06, PP和PME任务分配均衡, 且PP rank内任务负载也相对均衡, 由此带来绝对性能提升了19.3%. 当Nrank=100时, mdrun估算的Npme=28, PME/PP为1.67, 据对性能为47.73 ns/day. 当调整Npme=40时, PME/PP比为1.11, 由此带来绝对性能提升了22.8%.
合适的PME rank数可以根据tune_pme小工具估算, 亦可根据前面小规模测试数据估算. 前一种方法扫描计算所有可能情况, 计算比较耗时. 本文使用后一种方法. 例如对于3MGO体系, 在单节点Nrank=20时, Npme=8, PME/PP=1.03, 任务分配比较均衡. 由此推算, Npme≈0.4Nrank, 当Nrank为50时, PME独立rank数选择20较为合适, 当Nrank为100时, PME独立rank数选择40较为合适, 在实际计算时, 还需要通过PME/PP比例确定调整的方向.
对于DPPC体系, 从图6可以看出, 当Nrank(Npme)=100 (20)时, PME/PP任务分配不均(PME/PP=0.73)且PP任务负载不均衡率很高(Avg. imb%达到了32.5%), 当调整Npme=16时, PME/PP比值为1.03, PME和PP的任务分配已达到比较均衡, PP任务负载不均衡性亦得到了较大改观(Avg. imb降低到了3.4%), 性能提升了9.8%. PP任务负载不均衡性高时,与小并行规模类似, 还可以调节Nrank和Nth的相对数值, 进行优化, 例如当Nrank(Npme)=20(4)时, Avg. imb%降低到了3.8%, 绝对性能较Nrank(Npme)=100 (20)时候提升了20%.
另外, 负载不均衡情况都得到改善后, 与小规模并行情况相同, Nrank>Nth时, 计算的绝对性能更优. 因此为获取最佳绝对计算性能, 在实际计算中尽量选择较少的线程和较多的进程, 减少多线程开销, 使Domain数据本地化, 减少Cache一致性开销和socket间的通讯开销.
综上分析, 我们总结出了CPU并行时性能调优的方向或判据, 如图7所示.

图7 CPU并行时性能调优判据/方向图
①当存在PME独立rank, 且PME/PP比小于0.8或者大于1.2时, PME和PP任务分配不均衡较为明显,需要调整Npme来调整PME和PP的任务分配 (Npme可通过小规模数据测算).
②当没有Npme, 或PME和PP任务分配达到均衡时, 若PP rank内任务负载不均衡时(Avg. imb%<5%)通过调节增大Nrank和减少Nth的相对数值来减弱或消除不均衡性现象.
3.2 CPU与GPU异构并行方式
加入GPU卡后, 我们首先在单节点中测试CPU/GPU最佳配比(此处设定Nth=1, 先考察总核心数与GPU卡的最佳配比)
图8展示了3MGO和DPPC单节点内 CPU/GPU配比测试结果, 其中红色框使用了2个GPU, 绿色框使用了1个GPU, 结果表明在本测试硬件平台上, 3MGO体系采用18 CPU+1 GPU计算的绝对性能优于20 CPU+1 GPU, 我们推论本测试算例CPU/GPU的理论最佳配比约为18(对于DPPC体系, 最佳配比约为16), 限于节点CPU最大仅为20, 测试显示用满节点内所有CPU和GPU卡获得的绝对性能最佳(3MGO为29.46 ns/day, DPPC为28.88 ns/day), 从使用者角度来讲, 可以在同样时间内模拟更多步数. 从硬件有效利用来看, 添加第二个GPU, 对于DPPC体系更加有利(DPPC绝对性能提升了75.6%, 3MGO性能提升了28.3%), 可以综合考虑性能提升与硬件耗电造成的损失比重来决定全部用满CPU和GPU或者选择18CPU+ 1 GPU配比. 在本文中, 我们从使用者角度出发, 选择用满节点内所有CPU和GPU卡. 在以下的计算中, 我们选择的CPU/GPU均为20/2.

图8 3MGO和DPPC单节点内 CPU/GPU配比测试
上面测试CPU端不考虑线程, 接下来我们加入OpenMP线程的影响, 加入GPU后, 由于异构并行的影响, PP rank任务负载很容易出现较大不均衡现象,因此我们只关注每步力的计算的负载均衡和计算的绝对性能. 在下面的测试中Load imb%均在2.5%以下,因此不做单独记录分析.

图9 3MGO和DPPC体系多节点多线程测试数据图
图9 展示了两个体系多节点多线程测试结果, 图中隐藏了Nrank值, Nrank=20n/nth, n为节点数. 由图知,随着并行规模增大, 使用线程更有利于绝对性能的提升. 这是因为, 在较大并行度时, 使用进程和线程结合方式可以减少区域分解的数量和MPI ranks, 即间接减少了CPU-GPU-CPU之间的通讯开销, 因此计算性能优越性会逐渐显现. 但开启多线程会有一定开销,特别使对cache一致性开销和socket间的通讯开销, 线程并非开的越多越好. 根据图9测试结果, 大规模并行时选择线程数为2或5较为合适.

图10 3MGO和DPPC体系CPU和GPU计算性能对比图
值得注意的是, 当Nnode>1时, 由于每一个主机CPU计算时间比GPU计算时间慢(GPU的负载较少),增加MPI计算节点时, 使用GPU卡计算时性能会快速提高, 但在计算节点持续增加后, CPU-GPU-CPU之间的通讯开销也会增加, 因此如果计算节点继续增加, 使用GPU的加速效果就会越来越不明显(如3MGO体系从1节点到2节点并行效率近90%, 到10节点时效率下降到不足40%), 直至与CPU计算性能相近. 如图10,加入GPU后, 相较于纯CPU计算, 性能提升最高为2.4倍, 且随着并行规模的增加, GPU的加速效果下降.
在本测试中, 我们仅考虑了‘-nb’为cpu/gpu两种情况, 当短程非键相互作用相对长程非键相互作用力很多时(例如coulombtype=Reaction-field), 选择‘-nb’为gpu_cpu模式可能会更好的改进性能, 这种情况我们会在以后的测试中进行讨论.
4 总结
本文对GROMACS软件在单纯CPU和CPU/GPU异构并行计算环境下, 如何提升计算性能进行了较为深入的分析与研究. 对于单纯的CPU并行方式, 负载均衡水平是一个重要的考察指标. 在低并行度时, 这种负载不均衡主要是PP rank任务负载的不均衡; 高并行度时, PME独立rank与PP rank一起作用, PP/PME的任务分配不均是导致性能损失的主要原因. 测试结果显示, 在总并行数N一定情况下, 采用较多的进程,较少的线程更有利于计算性能的提高. 使用CPU/GPU异构并行计算时, 着重考虑CPU和GPU的相对运算性能和配比, 需测试决定最佳的CPU/GPU配比. 在多个节点并行时候, 需要考虑CPU-GPU-CPU通讯开销的影响以及线程开销. 通过实例测试可得每个rank使用2-5个线程会提高绝对运算性能.
我们从原理阐述到实例讨论, 为GROMACS的终端用户提供了性能优化的方向和依据, 帮助其更容易理解这个软件黑盒子并行优化机理, 乃至其它分子动力学模拟软件.
1 Abraham MJ, Murtola T, Schulz R, Páll S, Smith JC, Hess B, Lindahl E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. Softwarex, 2015, 1-2: 19–25.
2 Brooks BR, Bruccoleri RE, et al. CHARMM: A program for macromolecular energy, minimization, and dynamics calculations. Journal of Computational Chemistry, 1983, 4(2): 187–217.
3 Nelson MT, Humphrey W, Gursoy A, Dalke A, Kalé LV, Skeel RD, Schulten K. NAMD: A parallel, object oriented molecular dynamics program. International Journal of High Performance Computing Applications, 1996, 10(4): 251–268.
4 Pearlman DA, Case DA, Caldwell JW, Ross WS, Iii TEC, Debolt S, Ferguson D, Seibel G, Kollman P. AMBER, a package of computer programs for applying molecular mechanics, normal mode analysis, molecular dynamics and free energy calculations to simulate the structural and energetic properties of molecules. Computer Physics Communications, 1995, 91(1): 1–41.
5 Plimpton S. Fast Parallel algorithms for short-range molecular dynamics. J Comp Phys, 1995, 117, 1–19.
6 http://www.gromacs.org/.
7 Hess B, Kutzner C, Van DSD, Lindahl E. GROMACS 4: Algorithms for highly efficient, load-balanced, and scalable molecular simulation. Journal of Chemical Theory and Computation, 2008, 4(3): 435–47.
8 Gruber CC, Pleiss J. Systematic benchmarking of large molecular dynamics simulations employing GROMACS on massive multiprocessing facilities. Journal of Computational Chemistry, 2011, 32(4): 600–606
9 Darden T, York D, Pedersen L. Particle mesh Ewald: An N·log(N) method for Ewald sums in large systems. The Journal of Chemical Physics, 1993, 98(12): 10089.
10 ftp://ftp.gromacs.org/pub/manual/manual-5.0.7.pdf.
11 Essmann U, Perera L, Berkowitz M L, Darden T, Lee H, Pedersen LG. A smooth particle mesh Ewald method. The Journal of Chemical Physics, 1995, 103(19): 8577–8593.
12 Abraham MJ, Gready JE. Optimization of parameters for molecular dynamics simulation using smooth particlemesh Ewald in GROMACS 4.5. Journal of Computational Chemistry, 2011, 32(9): 2031–2040.
13 http://www.gromacs.org/documentation/acceleration_and_ parallelization.
14 Grubmüller H, Heller H, Windemuth A, Schulten K. Generalized Verlet algorithm for efficient molecular dynamics simulations with long-range interactions. Molecular Simulation, 1991, 6(1-3): 121–142.
15 Pall S, Hess B. A flexible algorithm for calculating pair interactions on SIMD architectures. Computer Physics Communications, 2013, 184(12): 2641–2650.
16 Kutzner C, Páll S, Fechner M, Esztermann A, deGroot BL, Grubmüller H. Best bang for your buck: GPU nodes for GROMACS biomolecular simulations. Journal of Computational Chemistry, 2015, 36(26): 1990–2008.
17 Sun Y, Liu Q. Differential structural dynamics and antigenicity of two similar influenza H5N1 virus HA-specific HLA-A* 0201-restricted CLT epitopes. RSC Adv, 2014, 5(3): 2318–2327.
18 Chiu SW, Pandit SA, Scott H, Jakobsson E. An improved united atom force field for simulation of mixed lipid bilayers. The Journal of Physical Chemistry B, 2009, 113(9): 2748–2763.
Parallel Computing Performance Analysis on GROMACS Software
ZHANG Bao-Hua, XU Shun
(Supercomputing Center, Computer Network Information Center, CAS, Beijing 100190, China)
Molecule dynamic (MD) simulation is used for simulation of atomic systems. It is a powerful tool for understanding relationships between microcosmic nature and macroscopic properties. In view of the problem of how to improve the performance of parallel MD simulations, in this paper taking the famous GROMACS software as an example, we study its implementation strategy on parallel computing performance, combining with the key principles of MD and the results of test cases, and we propose optimization strategies of performance under MPI and OpenMP parallel environment. It can provide theoretical and practical reference for optimizing performance of MD software. In addition, we also study that in the GPU heterogeneous parallel environment how to tune MPI/OpenMP and GPU to obtain the best performance.
molecule dynamic simulation; GROMACS; parallel computing
中国科学院青年创新促进会(2016156);“一三五”规划重点培育方向专项项目(CNIC_PY_1404)
2016-03-24;收到修改稿时间:2016-04-27
10.15888/j.cnki.csa.005471

