基于区域限定的奇异位置避免规划算法①
吕永军, 刘 峰, 郑飂默, 吴文江, 朱 良, 葛小川
1(中国科学院大学, 北京 100049)2(中国科学院大学 沈阳计算技术研究所, 沈阳 110171)3(沈阳高精数控智能技术股份有限公司, 沈阳 110171)
基于区域限定的奇异位置避免规划算法①
吕永军1,2, 刘 峰2,3, 郑飂默2,3, 吴文江2,3, 朱 良1,2, 葛小川1,2
1(中国科学院大学, 北京 100049)2(中国科学院大学 沈阳计算技术研究所, 沈阳 110171)3(沈阳高精数控智能技术股份有限公司, 沈阳 110171)
目前人们关于奇异位形的处理研究主要包括两大类, 一类是研究如何避免, 一类是研究如何通过奇异点.在分析了国内外关于奇异位形的研究基础上, 本文提出了基于空间区域限定的奇异位置避免算法. 其核心思想就是预先对机器人运动轨迹进行规划, 给出了奇异位置及邻近奇异位置的区域划分方法, 从而保证在笛卡尔空间规划时能规划出一合理的插值点, 同时也基于高次多项式曲线理论对关节空间规划做了优化, 保证了关节和末端运动的连续性、稳定性等. 通过6轴机械臂在四五六关节时的奇异为实例, 运用该算法对奇异的处理做了实例分析. 然后通过给定初始点和目标点的位姿等参数, 定时采样数据, 并利用MATLAB对规划前后获得的数据进行了图形仿真, 验证了该算法的正确性和可行性.
机器人; 轨迹规划; 奇异位形; 极限位置
我们知道对于工业机器人操作臂来说, 其无法避免的一个问题就是奇异位形, 由于自身结构特点, 无论采用何种运动学建模方法DH法或其他方法, 都无法避免, 至少在目前无法避免. 许多国内外的学者也一直致力于该问题研究与实践, 并发表了大量的理论学术成果[1-9], 在实际的工业应用中发挥了巨大作用.目前, 不管是对串联机器人还是并联机器人奇异位形处理问题的研究, 虽然已经提出了许多的奇异点处理方法, 但是综合这些方法的本质特点, 主要可以分为两大类:
第一类方法是在整个工作区中应用统一的控制策略, 通常包括一个连续的函数, 引入了对任务空间或机械臂关节空间的轻微变化, 使末端执行器避免了奇异区域[10-11]. 这一类方法通常会导致一个连续修改的雅可比矩阵或操作臂末端运动轨迹. 且对于这个连续性的函数, 在操作臂末端执行器远离奇异位置时是趋向于零的. 在接近奇异位置时, 引入一个对雅克比矩阵或任务空间的轻微调整, 使得避免雅可比矩阵病态即不可逆.
第二类方法是是对奇异区域进行分割, 从而对周围的奇异区域应用不同的控制算法. 这类方法的研究成果相比第一类较多[3-7,9], 这里不再赘述.
本文在结合上述的两类方法并针对不同类型奇异位形采用不同处理方法, 并主要针对内部奇异问题,从空间规划角度, 提出了一种基于机器人操作臂工作区域限定邻近奇异位置的控制处理算法, 如表1所示.

表1 奇异位形处理算法
1 奇异位置识别
操作臂奇异直观的物理表现就是在奇异处运动退化, 操作臂可操作的自由度减少, 而数学上则表示雅克比矩阵的行列式det(J(θ))=0, 即可得到该操作臂的奇异位置点. 完成奇异位置的识别后就可以对该点进行针对处理, 或通过一种路径规划算法避免该点,或通过一种算法能够使得操作臂末端执行器能够平滑稳定的通过该奇异点. 实际上, 事实并非如此, 关于操作空间中的奇异点并不具有严格的界限, 所以会产生操作臂不仅在奇异点而且在邻近奇异点处也会发生运动退化的情况. 所以可以定义一个奇异区阈值det0,若在该阈值内则称为奇异区, 大于该阈值的区则为非奇异区. 有了奇异区判断方法, 就可以在末端执行器轨迹规划时有效避开该奇异区, 第3节将对此做详细介绍.
2 极限位置奇异处理
首先极限位置奇异的产生是由于机器人操作臂自身结构限制导致的, 故对于该奇异的处理通常并不是人们考虑重点, 最有效的且在实际中的处理就是避免该奇异位置.
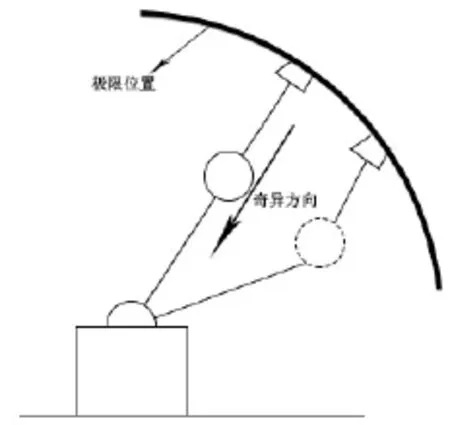
图1 平面2连杆机器人操作臂
不过, 也有相关学者利用了Null Space Motion(空空间运动)理论对极限位置奇异进行了研究[12], 如图1,显示了在极限位置的平面2连杆操作臂, 此时其操作臂末端执行器在奇异方向上将失去运动能力, 因为其两个节点速度产生的任务空间速度矢量垂直于奇异方向. 若给予该关节一个空空间的运动, 将产生末端执行器整体移动效果, 从而避免了奇异位置. 关于空空间理论在极限位置的研究请参考文献[9,12].
3 内部奇异位置处理
操作臂奇异直观的物理表现就是在奇异处运动退化, 操作臂可操作的自由度减少, 而数学上则表示雅克比矩阵的行列式 , 即可得到该操作臂的奇异位置点. 然而实际中的奇异点并不具有严格的界限, 所以会产生操作臂不仅在奇异点而且在邻近奇异点处也会发生运动退化的情况. 本文将该位置和其附近的区域称为奇异区. 进行奇异区定义在意义在于, 根据该定义可在进行末端笛卡尔规划时能规划出一个合适的位置, 从而绕过奇异区. 同时为保证末端插值点间轨迹符合期望轨迹, 具有连续和稳定性, 还需要对关节进行联动控制即进行关节空间规划. 整个算法的流程如图2所示.

图2 算法流程图
3.1 基于奇异区识别的末端轨迹规划
由于操作空间中的奇异点并不具有严格的界限, 不仅在奇异点而且在奇异点附近处也会发生运动退化的情况. 所以可以定义一个奇异区阈值 , 在阈值范围内则定义为奇异区. 当进行末端笛卡尔空间规划时对每个规划点进行判断, 选择符合的点, 从而避开奇异位置区.
设末端初始位姿(R1, P1)点a到目标位姿(R2, P2)点b. 根据一定的插补周期T=1/N(自适应插补周期算法[13])对运动轨迹进行插补, 并求出每一步的位姿. 则设第i步位置规划为P(i), 第i步姿态规划为R(i), 当末端沿直线运动时有:
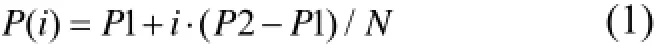
当末端沿圆弧运动时如图3, 设圆心O为(x0,y0,z0), P1为(x1,y1,z1), P2为(x2,y2,z2), Pi为(xi,yi,zi), 则有:
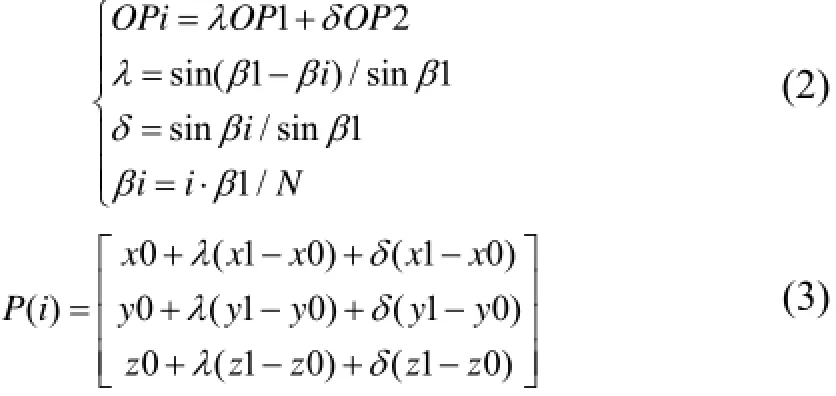
第i步的姿态R(i)相对初始姿态R1的旋转量设为Rot(f,θi), 则末端规划的第i位置的位姿量为:


图3 末端沿圆弧运动
根据解析法[6]求得第i位姿所在的雅可比矩阵J|T(i). 又J|T(i)为n阶方阵, 线性代数性质有:
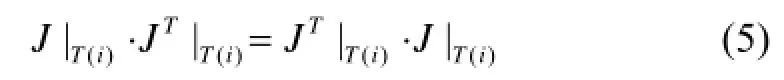
J|T(i)·JT|T(i)为一对称矩阵, 故对奇异区域Ω定义如下:
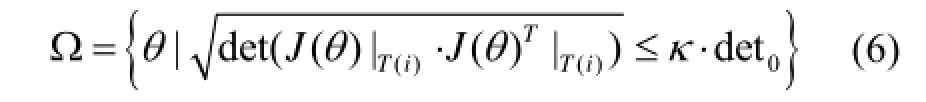
由于不同情况的奇异位置其包括的的区域定义不同, 其中系数κ就是为了获得误差更小的阈值值而引入的一个调节因子(试验中该阈值的经验值约为从而若在该阈值内则称为奇异区, 大于该阈值的区则为非奇异区. 这样通过式(6), 即可准确的对操作臂执行器的工作空间进行比较准确的划分有了奇异区判断方法, 就可以在末端执行器轨迹规划时有效避开该奇异区.
因为两个插值点之间的运动路径存在多种可能选择,仅仅完成末端的规划避开奇异位置可能导致与期望轨迹有所偏差, 同时也难保证运动的连续平滑性和稳定性.故还需要对关节进行运动控制, 即关节空间规划.
3.2 基于高次多项式曲线的关节运动规划
由于操作臂的运动是具有连续性、平滑和非线性的特点, 但是操作臂的每个关节运动却是线性的. 且末端位置和方向要随着时间推移而表现平稳, 机器人关节实际都有最大速度限制, 并且在这个限制下能在最小运动时间内完成尽可能多的操作, 速度不可任意选择, 太大和太小都会导致不可行轨迹(即奇异导致的情况). 并且通常速度和加速度以及加速度的导数都要求保证连续性, 要满足此条件可以用分段的高次(五次多项式)曲线实现[14], 这也是工业电机驱动常用的速度控制方式. 因此轨迹规划的实质就是获得满足运动控制的高次曲线算法.
设有函数及其一阶二阶导数分别表示关节位置、速度、加速度:
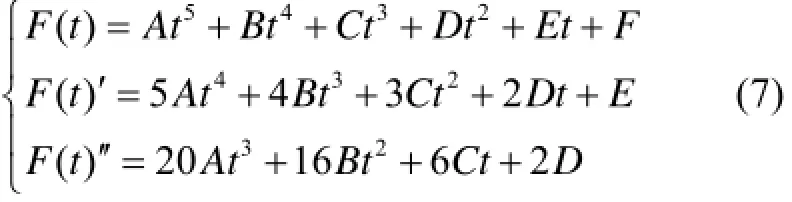
设初始时t=0, 下一时刻t=T, 相关函数表值如下表2.

表2 t=0、T时刻位置、速度、加速度值

上表写成矩阵形式如下:
将式(8)代入式(7)可得系数向量各项表达式:

将式(9)代入式(7)即可求得符合条件的关节位置、关节速度和关节加速度. 将该参数经过转换作为输入送往PMAC控制器, 由PMAC实现关节的实时运动控制.
4 算法验证与分析
首先六轴串联机械臂在4、6关节轴共线且关节角5等于零时发生奇异. 如图4左示意图, 要由a运动到b点位置, 若不通过式(6)绕过奇异区, 那么由a到b时,第四关节角度就会由θa突变到θb从而发生关节速度的瞬时改变, 导致运动失控并导致机构收到损坏.

图4 四五六关节奇异避免示意图
要避免关节4的瞬时改变, 在末端执行器接近到达奇异区时, 根据式(6)有a沿图4右示意图的蓝色弧线运动, 即保持5关节角不变, 使得运动路径能绕Z做圆弧运动, 避免关节速度瞬时突变从而避免了奇异问题.
机械臂末端执行器在a的末端初始位姿为Ta=[0,0,1,883.7;0,-1,0,0;1,0,0,700;0,0,0,1], 到目标点b的位姿为Tb=[0,0,1,883.7;0,-1,0,200;1,0,0,700;0,0,0,1],利用工具箱进行验证仿真运动. 轨迹规划采样时间为56毫秒, 并对实验中采集到的从初始点a到终点b输出的各关节角度数据通过处理, 利用MATLAB对规划前后的末端执行器的运动轨迹和各关节角的曲线进行仿真. 如图5、6为未采用式(4.2.2.3/4)限制条件时由空间位置a点运动到空间位置b点的一种轨迹曲线, 可见其轨迹曲线及加速度曲线并不满足平滑和连续性要求. 图7、8为优化限制条件后的轨迹曲线. 同时优化后各个六个关节的角度值、角速度、交加速度变化曲线如图9至14所示.

图5 未规划的末端轨迹曲线

图6 未规划的末端运动相对X、Y、Z轴变化曲线
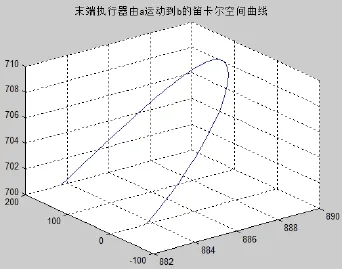
图7 规划后末端运动空间轨迹曲线

图8 规划后末端运动相对X、Y、Z轴变化曲线

图9 关节1角度值、角速度、交加速度变化曲线

图10 关节2的角度值、角速度、交加速度变化曲线
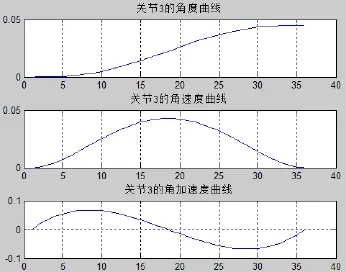
图11 关节3的角度值、角速度、交加速度变化曲线
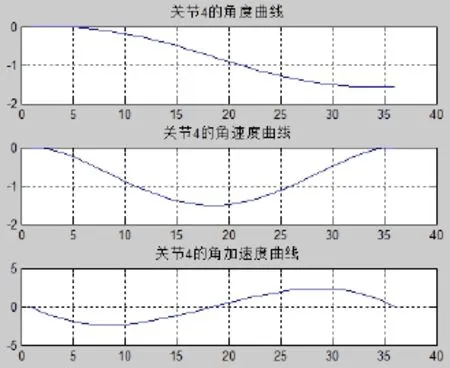
图12 关节4的角度值、角速度、交加速度变化曲线

图13 关节5的角度值、角速度、交加速度变化曲线

图14 关节6的角度值、角速度、交加速度变化曲线
从上述各图中可以观察到末端运动轨迹曲线变化情况, 以及每个关节有初始点运动到目标的的速度、加速度等变化情况, 从图中各曲线可以看到避过了奇异区, 保证了运动连续性, 各关节运动并未出现突变情况表现相对平滑, 表明了算法的正确和可行性.
6 结语
在分析了国内外关于奇异位形的研究基础上, 提出了基于空间区域限定的奇异位置避免算法. 从速度控制角度, 通过预先对机器人运动轨迹进行规划, 给出了奇异位置及邻近奇异位置的区域划分方法, 从而在笛卡尔空间规划时能规划出一合理的插值点, 在通过在关节空间时, 基于高次曲线理论对关节速度、加速度等的规划, 保证了关节和末端运动的连续性、稳定性等. 最后通过MATLAB进行实验了仿真, 仿真结果验证了该算法的正确性和可行性.
1 Chen G, Jia Q, Sun H. The study on algorithm for avoiding dynamics singularities of space robot. International Conference on Control and Automation, 2009.
2 Marani G, Kim J, Yuh J, et al. A real-time approach for singularity avoidance in resolved motion rate control of robotic manipulators. IEEE International Conference on Robotics and Automation, 2002. Proc. ICRA ’02. IEEE. 2002.
3 Merlet J. Singular configurations of parallel manipulators andGrassmann geometry. The International Journal of Robotics Research, 1989, 8(5): 45–56.
4 方跃法,陈集.机器人通过奇异位形的控制方法.齐齐哈尔大学学报:自然科学版,2002,18(1):67–70.
5 Tchon K, Muszynski R. Singular inverse kinematic problem for robotic manipulators: A normal form approach. IEEE Trans. on Robotics & Automation, 1998, 14(1): 93–104.
6 于靖军,刘辛军,丁希仑,戴建生.机器人机构学的数学基础.北京:机械工业出版社,2008.
7 谭民,等.先进机器人控制.北京:高等教育出版社,2007.
8 Liu H, Zhang T. A new approach to avoid singularities of 6-DOF industrial robot. 2010 International Conference on Mechatronics and Automation (ICMA). 2010.
9 Oetomo D, Jr MHA. Singularity robust algorithm in serial manipulators. Robotics and Computer-Integrated Manufacturing, 2009, 25(1): 122–134.
10 Liu H, Zhang T. A new approach to avoid singularities of 6-DOF industrial robot. 2010 International Conference on Mechatronics and Automation (ICMA). 2010.
11 Kim J, Marani G, Chung W, Yuh J. Task reconstruction method for real-time singularity avoidance for robotic manipulators. Adv Robot 2006, 20(4): 453–481.
12 邬林波.基于NSB方法的多机器人编队控制[学位论文].长沙:国防科学技术大学,2010.
13 冯蕊,刘鸿飞,高俊斌,等.工业机器人自适应生成插补周期的轨迹规划算法.机床与液压,2009,37(9):173–175.
14 Whitty M. Robotics, vision and control. Fundamental algorithms in MATLAB. Industrial Robot, 2012, 39(6): 75-85.
Singularity Avoidance Planning Algorithm Based on the Identification of Singular Configurations
LV Yong-Jun1,2, LIU Feng2,3, ZHENG Liao-Mo2,3, WU Wen-Jiang2,3, ZHU Liang1,2, GE Xiao-Chuan1,212
(University of Chinese Academy of Sciences, Beijing 100049, China) (Shenyang Institute of Computing Technology, University of Chinese Academy of Sciences, Shenyang 100171, China)3(Shenyang Golding NC Intelligent Tech. Co. Ltd., Shenyang 100171, China)
This paper firstly summarizes the research on the singularity in the past. One is the study of how to avoid it, the other is the study of how to pass the singular point. On the basis of previous studies, a new method is proposed to avoid the singular location based on the space region limited. The main point is to pre-plan the motion trajectory of the robot, and then give a method about how to differentiate the singular position and the adjacent singular position to ensure that a reasonable interpolation point can be planned during the Cartesian space planning. Meanwhile, based on the higher order polynomial theory, joint space planning is optimized to ensure the continuity and stability of joint and terminal motion. Taking 6 axis manipulator in wrist joint singular as an example, we use the proposed algorithm to analyze the process of the singular position. Given the parameters such as the initial point and the target point, the data obtained is simulated graphically in MATLAB, and the correctness and feasibility of the algorithm are verified.
robot; trajectory planning; singular configuration; extreme position
国产高档数控机床、系统及其技术在航空领域的综合应用验证及工艺研究(2014ZX04001051)
2016-03-24;收到修改稿时间:2016-05-05
10.15888/j.cnki.csa.005505

