融资融券交易与市场稳定性：基于动态视角的证据

刘 烨, 方立兵, 李冬昕, 李心丹

(南京大学工程管理学院, 南京 210093)

融资融券交易与市场稳定性：基于动态视角的证据

刘 烨, 方立兵*, 李冬昕, 李心丹

(南京大学工程管理学院, 南京 210093)

通过构建“外生信息冲击的门限自回归条件密度(TARCD-X)”模型，进而从动态的视角考察了融资融券实施前后，市场涨跌和交易量增减4种重要的信息冲击对下一期市场稳定性的影响具有怎样的差异，以及融资融券实施后，融资融券余额变动作为新的信息冲击如何影响下一期市场的稳定性.以波动性、暴涨暴跌的不对称性和暴涨暴跌的频繁性3个指标衡量市场的稳定性，研究发现：(1)12种影响关系中，除交易量减小对市场波动性的冲击作用在融资融券实施后有所放大之外，其他11种影响关系均未出现不利变化；(2)融资融券余额的变动没有显著增加市场的波动性和暴涨暴跌的频繁性，但其与暴涨暴跌的不对称性存在显著的相关关系.后者为构建股市暴涨暴跌的预警指标提供了实证依据.

融资融券； 市场稳定； 卖空； 条件密度

0 引 言

2010年3月31日，我国正式启动融资融券试点，允许符合条件的投资者向经纪公司借入资金(融资)并买入证券，或者借入证券(融券)并卖出.作为一项机制创新，融资融券交易的现实意义在于结束了我国股市成立20多年来没有卖空机制的历史.在经典的金融理论中，允许卖空交易被视为减小市场摩擦、平抑暴涨暴跌的一项必要举措.然而，在实务界，人们常常怀疑卖空机制会加剧市场动荡、破坏稳定性.那么，融资融券的实施到底如何影响市场稳定性呢？这显然是实务界尤其是监管层十分关心的问题.

本文认为，对这一问题的回答至少应从如下两个视角进行深入剖析，一是静态的视角，二是动态的视角.前者是较为传统的研究视角，相关文献十分丰富，如Bris等[1]、Fotak等[2]、Saffi和Sigurdsson[3]、Maggi和Fantazzini[4]以及Beber和Pagano[5]等；国内学者如廖士光[6]、杨德勇和吴琼[7]、王旻等[8]以及许红伟和陈欣[9]等.这类研究通常比较融资融券实施前后或卖空约束放松(收紧)前后市场稳定性指标的均值具有怎样的差异.动态视角则有所不同，其更加强调于描述市场稳定性指标的时变特征，进而考察融资融券这一机制创新前后，市场稳定性的动态过程具有怎样的差异.以波动性这一常见的稳定性指标为例，基于静态视角的研究通常比较融资融券前后两个样本期的平均波动性，而基于动态视角的考察通常是在刻画时变波动性的基础上，讨论其时变过程在融资融券实施前后是否发生变化.可见，动态视角与静态视角相比，其显著优势在于强调了市场稳定性的时变特征.具体说来，市场稳定性指标的动态变化往往与信息冲击的随机到达紧密相关，信息冲击的随机性决定了相关稳定性指标的时变性.基于动态视角的研究，可以深入考察上述信息冲击如何影响市场的稳定性，以及这种影响关系在融资融券实施前后是否发生变化、怎样变化.基于静态视角的研究则无法达到这一目的.

然而，令人遗憾的是，目前动态视角的研究还很不全面，相关认识有待深入.在同类文献中，万迪昉等[10]的研究比较具有代表性，他们以波动性作为市场稳定性指标，采用GARCH-M模型考察了融资融券交易由“试点”转为“常规”的一年半时间内，市场涨跌对波动性的影响出现了怎样的变化.但是，对市场的稳定性的评价仅仅用波动性评价还不够，还应包括暴涨暴跌的不对称性以及频繁性.另外，融资融券实施后，融资融券余额的变化作为市场披露的重要信息受到密切关注.那么，这一新生的信息冲击将对市场的稳定性产生怎样的影响呢？这是另一个十分重要但基于现有研究结果难以回答的问题.

鉴于此，本文构建了“引入外生信息冲击的门限自回归条件密度(TARCD-X)”模型，进而刻画了前期市场涨跌、交易量增减以及融资融券余额的变化等信息冲击与市场稳定性指标之间的动态关系.为了较为全面地衡量市场的稳定性，本文除了采用常见的波动性指标外，还用偏度衡量市场暴涨暴跌的不对称性，以及峰度衡量暴涨暴跌的频繁性.TARCD-X模型的关键优势在于，可以将市场涨跌、交易量增减和融资融券余额的变化等信息冲击变量，引入收益率的波动、偏度和峰度的动态过程，进而实现从动态角度考察市场稳定性的时变过程在融资融券实施前后具有怎样的特征.

1 文献回顾

关于实施融资融券或放松卖空限制是否会加剧市场动荡、损害市场的稳定性一直在实务界和学术界引起广泛争议.特别是在2007年—2009年的全球金融危机期间，市场一度怀疑卖空交易是导致股市急剧下跌和金融机构大面积倒闭的重要原因.因此，包括欧美等成熟市场在内的各国监管者相继推出各种不同程度的卖空禁令(short-selling bans)[1].然而，Fotak等[2]在对金融危机期间美国遭受“重创”的金融机构进行研究后发现，这些公司的股价暴跌跟卖空交易并无显著关系.国际货币基金组织(IMF)在其2010年发布的报告[11]中也指出，欧元区国家的卖空禁令不仅没有对危机期间金融机构的股价起到支撑作用，反而增加了价格的波动，损害了市场的稳定性.

事实上，除了波动性之外，市场收益率的偏度和峰度也是市场稳定性的两个重要衡量指标.其中，偏度描述了价格发生暴涨暴跌的不对称性；峰度通常用于描述资产价格发生暴涨暴跌的可能性是否高于正态分布给出的累积概率，即发生暴涨暴跌的频繁性.理论上，Miller[12]以及Diamond和Verrecchia[13]的研究认为，卖空约束会抑制利空信息的揭示过程而导致股价容易被高估，增加暴涨的可能性.Hong和Stein[14]则进一步指出，被抑制的利空信息往往会在积累一段时间后，在未来市场下跌时集中释放，从而导致市场在没有任何重大利空信息的驱动下“崩盘(crashes)”，暴跌的可能性因此而增加.Bai等[15]认为卖空约束不利于知情交易者的信息揭示，从而降低了资产价格的信息含量.不知情交易者因此面临较大的逆向选择风险，价格的波动性也就内生地增加了.可见，理论研究大多认为，放松卖空限制有助于提高市场的稳定性，至少无损于稳定性.

实证研究中，Bris等[1]对全球46个市场的卖空限制情况进行对比后指出，限制卖空无助于削弱暴跌高于暴涨的可能性，即难以缓解收益率的负偏风险.Saffi和Sigurdsson[3]以借贷余额作为卖空约束程度的代理变量，以收益率的波动、偏度和峰度作为衡量市场稳定性的指标，对全球26个国家和地区的股票市场进行研究后发现，放松卖空约束与价格的稳定性并无显著关系.Maggi和Fantazzini[4]对全球31个新兴市场进行比较后指出，允许卖空的市场比禁止卖空的市场具有更低的波动性和峰度，而收益率的偏度在不同的禁止卖空市场中各有不同，有的比允许卖空的市场低，有的则比较高.Chang等[16]对香港市场股市中允许卖空的个股和不允许卖空的个股进行比较后研究发现，前者收益率具有较高的波动和较低的正偏度.王旻等[8]利用台湾证券市场的融资融券交易数据进行研究后指出，融资买空与融券卖空交易并未显著影响整个市场的波动性水平.廖士光和杨朝军[17]利用香港股票市场的数据研究表明，对于整个股票市场而言，卖空机制推出后，市场波动性加大，但Granger因果检验结果证实市场波动性的增加并非由卖空交易引发.廖士光和杨朝军[18]对台湾股市研究指出，卖空机制的引入不仅没有加剧市场的波动，反而可以对市场的波动起到平抑作用.许红伟和陈欣[9]对中国股市的研究则指出，融资融券机制的推出能够显著减少股价发生大幅下跌的概率，却无助于减少收益率的峰度.究其原因，他们认为出现上述结果的原因可能是融资业务和融券业务发展的极端不对称导致的*从沪深两市的融资融券余额来看，融资交易的占比长期居于95%以上，而融券交易的占比在绝大部分情况下不足5%(参见本文的样本描述)..这类研究大多静态地比较市场的稳定性指标——波动、偏度和峰度在卖空约束放松或收紧前后具有怎样的差异.

基于动态视角的研究如Bohl等[19]采用GARCH、机制转换GARCH等模型考察了卖空约束收紧前后市场的波动性具有怎样的差异，并发现卖空约束收紧后，市场的波动性显著增加了.Devaney[20]也采用GARCH类模型对美国证监会(SEC)宣布纳入卖空禁令的房地产信托公司(REIT)股价的波动性进行了比较，结果也拒绝了卖空禁令会缓解波动性.万迪昉等[10]基于GARCH-M、EGARCH-M模型考察了融资融券业务推出前后，市场涨跌对股市波动性的影响具有怎样的差异，并指出金融创新能够促进交易所自律监管功能的发挥.由此可见，这些研究虽然进行了动态建模但很少分析卖空约束放松或收紧前后，相关信息冲击对波动性的影响关系发生了怎样的变化.而这才是基于动态视角进行研究的关键所在.当然，除了收益率波动过程具有显著的时变性之外，近年来也有不少研究指出，收益率的偏度(暴涨暴跌的非对称性)和峰度(暴涨暴跌的频繁性)也存在显著的时变性[21-25].因此，要更加深入、全面地考察融资融券这一机制创新对市场稳定性的影响，应综合考察波动性、偏度和峰度等稳定性指标的动态过程发生了怎样的变化.

纵观现有文献，基于静态视角的研究，无论是“横向”比较，即在不同卖空约束程度的市场间比较，或是“纵向”比较，即对同一市场在卖空约束放松(收紧)前后进行比较，其研究结果均难以回答市场稳定性的动态过程是否发生改变、怎样改变.基于动态视角的研究往往没有考虑收益率的偏度和峰度等两个重要的稳定性指标，因而不够全面.此外，基于现有研究的结果还难以回答融资融券余额的变化如何影响市场的稳定性.众所周知，融资融券余额是反映投资者买空、卖空行为的重要变量，其变动情况较为细致地跟踪了市场买空、卖空交易的运动轨迹.因此，研究融资融券余额的变化与市场稳定性的关系可以进一步考察投资者买空、卖空行为对市场的稳定性会产生怎样的冲击作用.

2 TARCD-X模型的构建与估计

设市场的收益率为rt，其条件均值为μt，条件波动、条件偏度和条件峰度分别为σt、λt和ηt.这三个指标构成了本文用于衡量市场稳定性的主要指标，下标t表示这三个指标具有时变性.于是，市场收益率rt可以表示为如下随机过程

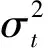
(1)

其中Ψt-1表示第t期可以获得的信息集.

关于条件均值μt，考虑如下模型

μt=u0+u1rt-1

(2)

对于金融市场的收益率来讲，其价格的效率性确保了一阶自回归足以刻画收益率之间的自相关关系.这是因为即便是一个弱势有效的市场，过去的收益率已经不具有对未来收益率的预测能力.因此，选择一阶自回归描述收益率自相关特征是合理的.

关于条件波动过程σt，考虑到收益率的波动过程具有“聚集性”和“杠杆效应”等典型事实，以及为了规避模型参数的非负性约束，这里选择Nelson[26]提出的指数GARCH(EGARCH)模型

(3)

(4)

(5)

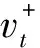
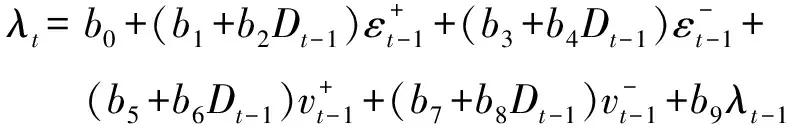
(6)

(7)

由上述设定可以看出，式(1)中关于收益率分布形态的设定需要同时引入均值、波动、偏度和峰度等参数.为此，本文选择Hansen[21]提出的有偏学生-t(SkewT)分布.其概率密度函数如下

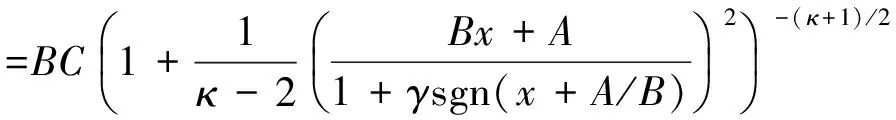
(8)

其中x定义为标准化收益率(rt-μt)/σt；γ和κ分别是偏度系数和自由度；sgn(·)是符号函数；A、B和C都是γ和κ的函数

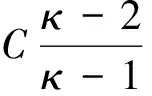
γ>0和γ<0分别表示概率分布为正偏和负偏，而且|γ|越大，偏斜程度越严重；当γ=0时，分布是对称的，退化为传统的学生-t分布；自由度κ刻画了分布的尖峰、厚尾程度.与传统的学生-t分布类似，对于SkewT分布来讲，“尖峰”和“厚尾”也是一致的，即κ越小，“峰”越“尖”，“尾”越“厚”，价格发生暴涨暴跌的频繁性越高，峰度越大，反之亦反之.因此，SkewT分布足够灵活，可以较好地反映收益率的条件高阶矩特征.更为重要的是，与三阶和四阶中心矩等偏度和峰度的统计定义相比，SkewT分布的偏度系数γ和自由度κ更为直接地刻画了收益率分布的不对称程度和尖峰、厚尾程度，因此，更加符合本文关注于价格暴涨暴跌的对称性和频繁性特征的研究主旨.根据SkewT分布的定义，偏度系数γ应具有如下取值范围-1<γ<1，而自由度κ应满足3<κ<30.为使式(6)和式(7)产生的偏度和自由度系数符合此范围，Hansen[21]建议用Logistic函数Λ(l,u)(x)=l+(u-l)/(1+e-x)将λt和ηt分别映射到(-1, 1)和(3, 30)的区间内.考虑到γ和κ的时变性，记

γt=Λ(-1,1)(λt)，κt=Λ(3,30)(-ηt)显然，λt越大，γt越大，收益率越倾向于正偏，暴涨高于暴跌的可能性越高；ηt越大，κt越小，尖峰、厚尾程度越严重，暴涨暴跌频繁性越高.

综合式(1)—式(8)，需要估计的参数来自四个方程，即均值方程(2)的θ1=(u0,u1)，条件波动方程式(3)的θ2=(a0,a1,a2,…,a9)，条件偏度方程(6)的θ3=(b0,b1,b2,…,b9)以及条件峰度方程(7)的θ4=(c0,c1,c2,…,c9).在Ψt-1给定的情况下，可以通过极大化如下对数似然函数得到上述参数的估计值

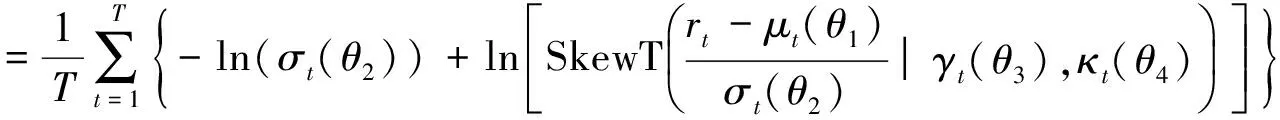
(9)

其中θ=(θ1,θ2,θ3,θ4).

为进一步考察融资融券实施后，融资融券余额的变化对市场稳定性的影响，考虑将相关变量引入稳定性指标的动态过程.记Mt和St分别表示第t期市场的融资余额和融券余额，二者的对数变化mt和st分别按如下方法计算

mt=lnMt-lnMt-1,st=lnSt-lnSt-1

(10)

当观测值为融资融券后样本时，式(5)、式(6)和式(7)可改写为

(11)

(12)

(13)

无论是将收益率的波动、偏度和峰度的动态过程设定为式(5)、式(6)和式(7)，亦或式(11)、式(12)和式(13)，两种设定都刻画了前期价格涨跌、前期交易量增减、融资融券余额变化等外生信息变量(记作“X”)对三种稳定性指标的冲击作用.此外，两种设定中也都考虑了外生信息以“0”为门限值(threshold)的非对称冲击.因此，本文将其称为“外生冲击的门限自回归条件密度(TARCD-X)模型”.为了便于表述，在本文接下来的内容里，将式(5)、式(6)和式(7)设定下的模型记为“TARCD-X1”模型，将式(11)、式(12)和式(13)设定下的模型记为“TARCD-X2”模型.这两个模型的参数估计均采用极大似然方法，估计过程使用Eviews编程实现.由于模型的待估参数较多，实际估计时，参数的初值对似然函数的极大化过程影响较大.因此，本文采用从简单到复杂的过程，将各个变量逐个加入模型中，并以前一个模型估计的结果作为下一个模型的初值，从而完成最终的模型估计.

3 样本描述及一些初步的结果

自2010年3月31日融资融券试点正式启动至2013年1月25日扩容以前，纳入融资融券范围的股票主要来自沪深300指数的部分成分股.因此，本文的实证研究以沪深300指数(HS300)的日百分比对数收益率为样本，进而从市场的层面考察融资融券的实施如何影响稳定性.与现有研究仅考察纳入融资融券范围的股票相比，其必要性在于，没有纳入融资融券范围的股票不可避免地会受到前者价格变化的影响.因此，仅仅以融资融券标的股票为研究对象并不能较为全面地评价这一机制创新对整个市场的影响.

本文的样本期间选择2009年1月5日至2013年3月29日.其中，2009年1月5日至2010年3月30日为融资融券前样本；2010年3月31日～2013年3月29日为融资融券后样本.融资融券交易前样本以2009年1月5日作为起点的原因在于，2006年至2008年的中国股市经历了长达两年的牛市和一年的熊市.在此期间，沪深300指数从2006年初的937点一路上涨，直到2007年10月16日达到5 875点的最高位置，然后又持续下跌，并于2008年11月4日跌至1 627点的最低水平.这一“过山车式”的暴涨暴跌过程如果不从样本中剔除，可能使研究结果难以令人信服.当然，作为一个补充的检验，本文的稳健性检验部分仍然将其纳入研究样本.

如此取样可能带来的一个新的问题是，融资融券前后样本容量差距较大.前者共包括300个观测值，而后者约为前者的2.4倍，共728个观测值.但本文认为后者容量相对较大是必要的.首先，融资融券交易作为一项机制创新，投资者需要一个适应过程，监管者也需要对市场的运行情况观察一段时间后才能全面推行.事实上，融资融券交易由“试点”转为“常规”是以2011年11月25日《上海证券交易所融资融券交易实施细则》正式施行为标志的.2010年3月31日至2011年11月24日期间的样本仅为试运行期间的样本.其次，在上述样本中，融资融券作为“常规”业务的样本量(2011年11月25日至2013年3月29日)共计324个交易日，与融资融券前的样本量是比较接近的.当然，由于本文着眼于市场稳定性的动态过程，为了保持其时间序列上的连续性，不再剔除2010年3月31日至2011年11月24日这段试点期间的样本.

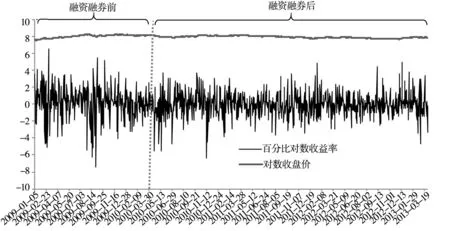
图1 沪深300指数的对数收盘价及收益率(百分比)

Fig.1 Logarithmic close price and returns (in percent) of HS300 index

图1描绘了整个样本期间沪深300指数的对数收盘价和百分比对数收益率的折线图.从图中可以看出，沪深300指数在整个样本期的走势是比较平稳的.表1对融资融券前后沪深300指数的收益率(rt)、交易量的对数变化(vt)以及融资融券后融资融券余额的对数变化(mt和st)进行了描述性统计.

从表1可以看出，融资融券后，沪深300指数收益率的标准误比融资融券前有所下降.这就意味着，收益率的波动程度比融资融券前有所改善.从收益率的偏度来看，虽然两个样本期均为负值，但绝对值从0.541 7下降到0.137 3，即融资融券交易实施后，收益率的负偏度也削弱了，暴涨暴跌的不对称性有所缓解.

相比之下，刻画暴涨暴跌频繁性的峰度在融资融券后相对较大，这与前述理论预示不尽一致.但是，从沪深300指数暴涨暴跌的次数和频率来看，融资融券实施前，涨幅大于5%的次数为3次，频率约为1%(≈3/300)，跌幅大于5%的次数为5次，频率约为1.67%(≈5/300)；相比之下，融资融券实施后，涨幅大于5%的次数和频率为0，而跌幅大于5%的次数和频率分别为3和0.41%(≈3/728).由此可见，融资融券实施后，市场发生暴涨暴跌的频繁性大幅减小，特别是暴跌的频率减小为原来的1/4左右.这些结果表明，暴涨暴跌的频繁性和幅度相对于融资融券前均有所改善.另外，从收益率的极端值来看，融资融券实施前的最大涨幅和跌幅分别为6.46%和7.37%，而融资融券实施后的最大涨幅和跌幅分别为4.93%和6.42%.从收益率暴涨暴跌的分布(样本分位数)来看，融资融券实施后，95%和85%水平上的分位数均小于融资融券实施前相应水平上的分位数，而5%和15%水平上的分位数均大于融资融券实施前的分位数.这就从暴涨暴跌的分布情况反映了融资融券实施后市场的稳定性相对较好.综合上述描述性统计结果可以看出，大部分市场稳定性指标均反映了融资融券的实施提升了市场的稳定性.这与现有的基于静态视角的研究结果是一致的.

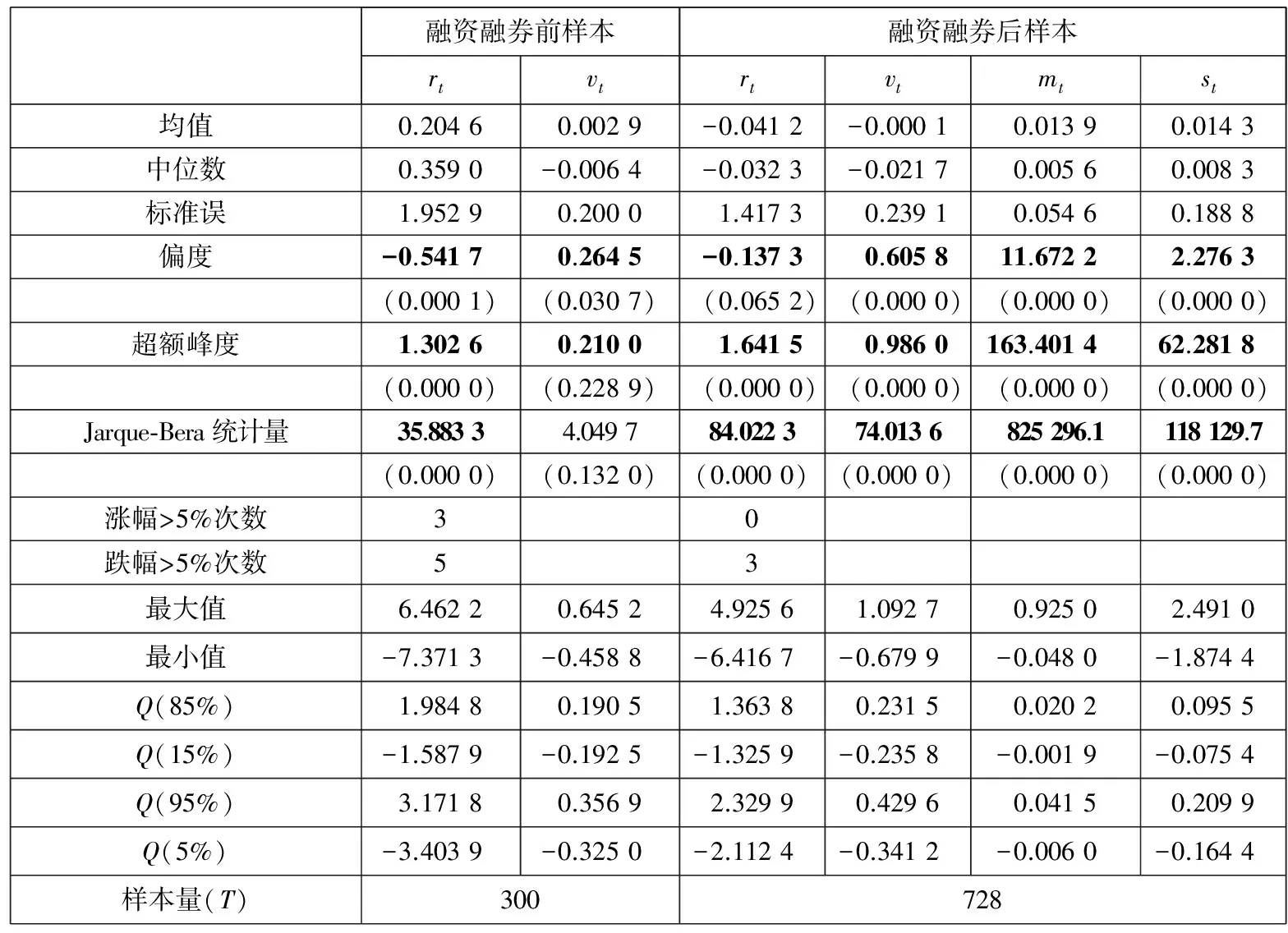
表1 融资融券前后样本的描述性统计

从交易量对数变化(vt)的分布情况来看，无论是极端值还是四种分位数值，融资融券后的绝对值均大于融资融券前的结果.这说明，融资融券实施后交易量的大幅增加和减少均比融资融券前变化的较为剧烈.这与融资融券这一机制创新所带来的杠杆交易是有关的.除此之外，从vt的偏度和峰度而言，融资融券后的偏度和峰度均高于融资融券前的样本.这说明融资融券实施后，市场的交易量比融资融券前更加易于出现大幅增减，且大幅增加的可能性相对更高.这些结果也都与融资融券给市场带来的杠杆交易是一致的.

图2给出了融资融券实施后，各交易日融资余额的对数(lnMt)、融券余额的对数(lnSt)以及融资余额占融资融券余额比重(Mt/(Mt+St))的折线图.从图2可以看出，融资余额和融券余额均成增长趋势.结合表1对融资融券余额的对数变化给出的描述性统计结果来看，融资融券余额的日平均增幅为1.3%～1.4%.从图2还可以看出，融资余额增长趋势相对较为稳定，而融券余额的增长过程具有较大的变异.这也可以从表1给出的相关描述性统计结果得到支持.首先，从标准误来看，融资余额对数变化(mt)的标准误不到融券余额对数变化(st)标准误的1/3.其次，从mt和st的极端值以及六种水平的分位数也可以得出类似的结论.融资余额的日最大涨幅为92.50%，最大跌幅为4.80%，但融券余额的日最大涨幅为249.10%，而最大跌幅为187.44%.最后，从分位数来看，mt的50%以上的三种分位数均小于st相应水平上的分位数，而mt在50%以下的三种水平上的分位数均大于st相应水平上的分位数.另外，值得注意的是，从融资余额在融资融券余额中的占比(图2)来看，融资余额长期占据绝对优势，占比一直维持在95%以上.这再次应证了现有研究给出的结果，即我国的融资融券交易存在严重的“跛足”现象.

综上所述，相关描述性统计结果已经初步说明了，融资融券交易实施后，沪深300指数的价格变化比融资融券前更加稳定，而交易量则比融资融券前变化得更加强烈.另外，融资融券实施后，市场的融资余额呈现较为稳定的增长趋势；融券余额虽然在总体上也呈增长趋势，但其变化相对较为剧烈.

图2 融资融券余额日折线图

Fig.2 Line chart of daily account of margin trading

4 实证结果

本文的实证结果包括如下两个部分：一是基于全样本估计式(5)、式(6)和式(7)设定下的TARCD-X1模型，进而考察前期的价格和交易量的变化如何影响市场波动性、暴涨暴跌的不对称性(偏度)和频繁性(峰度)等稳定性指标，以及这种影响关系在融资融券实施前后是否发生变化；二是基于融资融券后的样本估计式(11)、式(12)和式(13)设定下的TARCD-X2模型，从而考察前期的价格、交易量、融资融券余额的变化等信息冲击如何影响市场的波动性、偏度和峰度等稳定性指标.

4.1 市场稳定性的动态过程： 融资融券前后的比较

从TARCD-X1模型的设定可以看出，式(5)、式(6)和式(7)总共刻画了12种影响关系，即市场的上涨和下跌、交易量的增大和减小4种信息冲击与波动性、暴涨暴跌的不对称性和频繁性3种稳定性指标间的动态关系.三个方程的参数估计结果如表2所示.

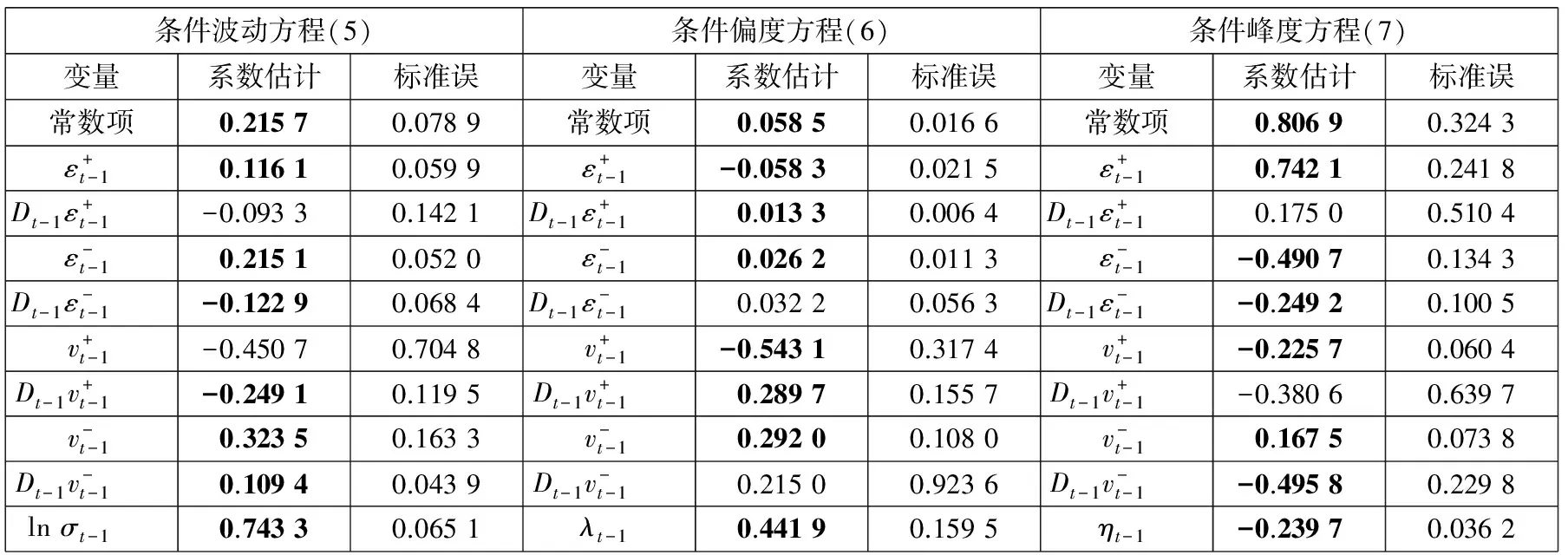
表2 信息冲击与市场的稳定性： TARCD-X1模型的估计结果

注：1)TARCD-X1模型设定为式(5)、式(6)和式(7)，估计的样本期为2009年1月5日至2013年3月29日；2)虚拟变量Dt-1用于控制融资融券后各信息冲击对收益率条件波动的影响.3)以粗体显示的数值表示其p-值小于显著性水平10%.

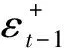
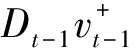
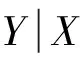
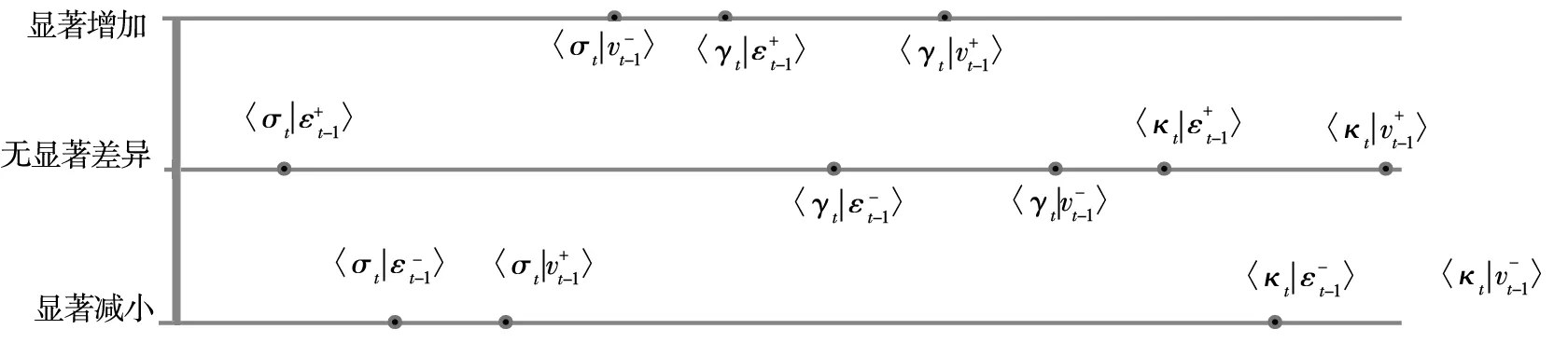
图3 融资融券前后信息冲击对市场稳定性指标的影响比较

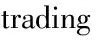
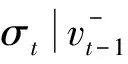
4.2 融资融券后相关信息冲击对市场稳定性的影响

表3 信息冲击与市场的稳定性： TARCD-X2模型的估计结

注：1)TARCD-X2模型设定为式(11)、式(12)和式(13)，估计的样本期为2010年3月31日至2013年3月29日；2)以粗体显示的数值表示其p-值小于显著性水平10%.

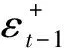
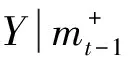
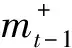
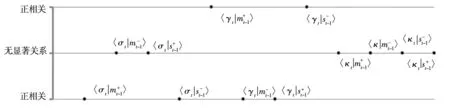
图4 融资融券余额变化与市场的稳定性

Fig. 4 The impact of changes of margin account on market stability

综上所述，在TARCD-X2模型中，价格和交易量的变化与三个市场稳定性指标的关系与TARCD-X1模型是一致的.除此之外，在控制了前期价格涨跌和交易量增减后，融资融券余额的变化并未显著增加市场的波动性和峰度(暴涨暴跌的频繁性)，且其对预期偏度(暴涨暴跌的不对称性)具有一定的短期预测能力.具体来说，当融资余额减少或融券余额增加时，市场暴跌的可能性增加，而暴涨的可能性减小，即需要注意防范负偏风险.

5 稳健性检验

为了检验上述结果的稳健性，本文进行两个方面的稳健性检验.首先，考虑将样本的起始时间调整为沪深300指数的挂牌日期，即利用2005年4月8日至2013年3月29日共1 939个观测值重新估计TARCD-X1模型.虽然2006年～2008年中国股市经历了一次前所未有的“牛转熊”行情，但不能排除这种行情的出现本身也可能是因为市场缺乏做空机制.因此，本文前面的研究中，将样本的起点选为2009年1月5日实际上是一种保守的做法，即提高了拒绝原假设的可能性.作为稳健性检验，进一步将样本期提前到2005年4月8日也是有益的尝试.

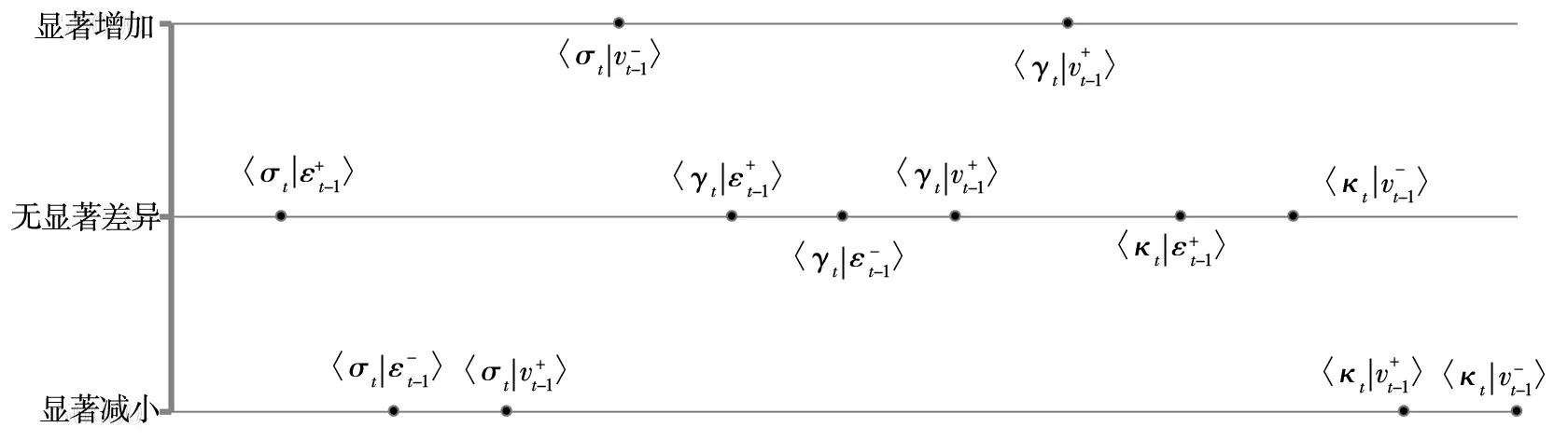
图5 融资融券前后信息冲击对市场稳定性指标的影响比较： 替代样本

Fig. 5 Comparison of the impact of information shock on market stability around margin trading: Based on the alternative sample

如图5所示*限于篇幅，稳健性检验的详细数据这里从略，但欢迎感兴趣的同仁来信索取.，虽然模型系数的显著性与图3的结果有一定差异，但从比较的结论来看，4种信息冲击对3种稳定性指标的12种影响关系中，也只有交易量的负向冲击与收益率波动性之间的关系在融资融券后显著增加，其他11种影响关系均未产生不利变化.因此，总体来说，市场稳定性指标的动态变化在融资融券实施后并未发生较大的不利变化.

本文进行的第二个稳健性检验是考虑到投资者大多存在风险规避心理，故而将“收益-风险”关系引入模型的均值方程并重新估计模型.这是因为，在前述研究中，TARCD-X1和TARCD-X2模型的均值方程均被设定为AR(1)的形式.这种设定形式忽略了信息冲击所引起的波动性风险与预期收益之间的关系，而这种“收益-风险”关系反映了投资者的风险规避心理对市场稳定性可能产生的影响.鉴于此，考虑将式(2)调整为

μt=u0+u1rt-1+φσt

(14)

其中σt反映了预期的波动性，系数φ刻画了收益率的期望值μt与预期的波动性风险之间的相关性.将式(14)与式(5)、式(6)和式(7)联合亦或与式(11)、式(12)和式(13)联合即可得到两种新的模型，这里分别记为TARCD-X3和TARCD-X4模型.

图6 融资融券前后信息冲击对市场稳定性指标的影响比较： 基于TARCD-X3模型

进一步比较图4和图7的结果可以发现，融资融券实施后，TARCD-X4模型所给出的融资融券余额的变化对市场稳定性的12种影响关系中，10种结果与TARCD-X2的结果是类似的.不同的是，在控制了“收益-风险”关系后，TARCD-X4模型的结果显示，融资余额和融券余额的增加对暴涨暴跌频繁性冲击作用显著减弱.这就进一步说明了，TARCD-X2模型所给出的融资融券余额对市场稳定性的影响中，有部分影响效果被投资者所要求的波动性风险补偿抵消了.

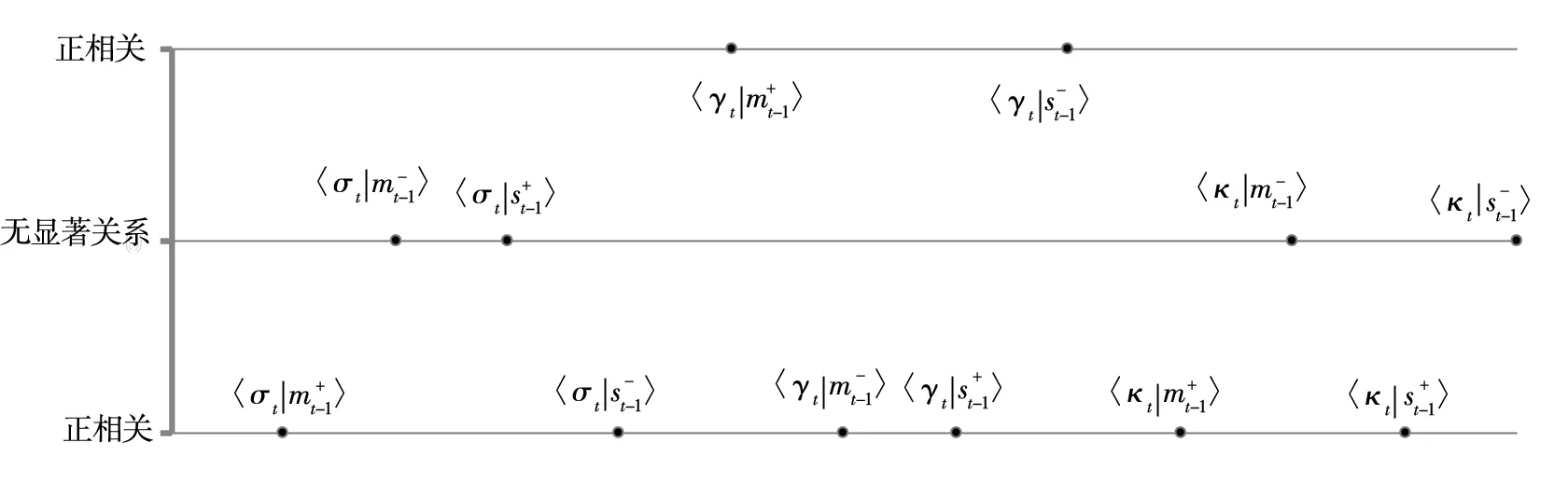
图7 融资融券余额变化与市场的稳定性： 基于TARCD-X4模型

Fig. 7 The impact of margin account changes on market stability: Based on TARCD-X4 model

综合上述稳健性检验的结果可以看出，市场涨跌和交易量增减4种信息冲击对市场稳定性的影响，在控制了“收益-风险”关系后，并未出现显著的不利变化.另一方面，从融资融券余额的变化作为新的信息冲击，对市场稳定性的影响也不会因为控制了“收益-风险”关系而恶化.因此，总的来说，在对投资者的风险规避心理所造成的影响加以控制后，本文实证研究部分所给出的结果均未出现不利变化.

6 结束语

为较为全面地考察融资融券交易对市场稳定性的影响，有必要从静态和动态两个视角进行深入研究.从已有文献来看，相关研究大多着眼于前者，即考察市场在不同程度的卖空约束条件下，其稳定性具有怎样的差异.这就忽略了市场稳定性指标应当具有的时变性特征.相比之下，动态视角着眼于市场稳定性时变过程在融资融券实施(放松卖空约束)前后是否发生变化、怎样变化.具体说来，基于动态视角的研究，可以将市场涨跌、交易量增减和融资融券余额的变化等重要的信息冲击引入市场稳定性指标的时变过程，进而更加深入地回答如下两个问题：一是市场涨跌和交易量增减等重要的信息冲击如何影响市场的稳定性，以及这种影响关系在融资融券前后具有怎样的差异；二是融资融券余额作为新的信息冲击会对市场的稳定性产生怎样的影响.此二者显然是十分重要而基于静态视角往往难以回答的问题.

鉴于此，本文提出了“外生信息冲击的门限自回归条件密度(TARCD-X)”模型，进而从动态的视角考察了前期市场涨跌和交易量增减等4种信息冲击对市场稳定性的影响在融资融券实施前后发生了怎样的变化.TARCD-X模型的显著优势在于可以将这4种信息冲击同时引入市场的波动性、暴涨暴跌的不对称性和暴涨暴跌的频繁性3个稳定性指标的时变过程，从而考察这12种影响关系在融资融券实施前后是否存在差异.此外，基于TARCD-X模型还可以考察融资融券余额的变化作为新的信息冲击如何影响市场的稳定性.以沪深300指数为样本，研究发现：首先，12种影响关系中，除了交易量减小对市场波动性的冲击作用有所放大之外，其他11种影响关系均未出现不利变化；其次，融资融券余额的变动作为新的信息冲击没有显著增加市场的波动性和暴涨暴跌的频繁性；最后，融资融券余额的变动与暴涨暴跌的不对称性存在显著的相关关系.具体说来，融资余额增加和融券余额减少预示着市场出现暴涨的可能性增加，而融资余额减少和融券余额增加预示着市场出现暴跌的可能性增加.因此，融资融券余额的变化对市场暴涨暴跌的不对称性具有一定的预测能力，这就为构造预警指标、防范市场的暴涨暴跌风险提供了有益的参考.

融资融券机制的实施结束了我国股市没有卖空机制的历史，但卖空机制的引入究竟能否减小市场摩擦、提升市场效率、促进市场稳定一直颇受关注.本文的研究只是经验地从动态的视角考察了融资融券实施前后市场稳定性发生了怎样的变化.但如何解释上述结果还有待于构建理论模型进行深入分析.例如，通过构建理论模型，研究卖空限制的市场环境下，价格的波动性、暴涨暴跌的非对称性和频繁性是如何形成的将是重要的研究内容.另外，对资产价格形成过程的深入考察，一种新兴的金融学分支——计算实验金融学(agent-based computational finance, ACF)广受青睐.与经典的金融理论与实证研究的范式不同，计算实验金融研究遵循相应的市场制度安排，赋予微观主体特定的行为模式以及相应的学习机制，强调市场(理性的或有限理性的)主体间的微观交互，进而揭示市场的运行特征与规律.基于计算实验环境，更为细致地研究放松卖空限制如何影响市场的稳定性将是未来极具创新性和实践价值的研究方向.

[1]Bris A, Goetzmann W N, Zhu N. Efficiency and the bear: Short sales and markets around the world[J]. Journal of Finance, 2007, 62(3): 1029-1079.

[2]Fotak V, Raman V, Yadav P K. Naked short selling: The emperor’s new clothes?[R]. Working Paper, Oklahoma: University of Oklahoma, 2009.

[3]Saffi P A C, Sigurdsson K. Price efficiency and short selling[J]. Review of Financial Studies, 2011, 24(3): 821-852.

[4]Maggi M, Fantazzini D. Chapter 23: Short Selling in Emerging Markets: A Comparison of Market Performance During The Global Financial Crisis[M]. Handbook of Short Selling, Waltham: Elsevier, 2012： 339-352.

[5]Beber A, Pagano M. Short-selling bans around the world: Evidence from the 2007-2009 crisis[J]. Journal of Finance, 2013, 68(1): 343-381.

[6]廖士光. 融资融券交易价格发现功能研究——基于标的证券确定与调整的视角[J]. 上海立信会计学院学报, 2011, (1): 67-76. Liao Shiguang. Study on the price discovery function of margin purchase and short sale transaction: From the aspect of underlying securities determination and adjustment[J]. Journal of Shanghai Lixin University of Commerce, 2011, (1): 67-76. (in Chinese)

[7]杨德勇, 吴 琼. 融资融券对上海证券市场影响的实证分析——基于流动性和波动性的视角[J]. 中央财经大学学报, 2011, (5): 28-34. Yang Deyong, Wu Qiong. Empirical research on the impact of margin trading on liquidity and volatility of Shanghai security market[J]. Journal of Central University of Finance & Economics, 2011, (5): 28-34. (In Chinese)

[8]王 旻, 廖士光, 吴淑琨. 融资融券交易的市场冲击效应研究——基于中国台湾证券市场的经验与启示[J]. 财经研究, 2008, (10): 99-109. Wang Min, Liao Shiguang, Wu Shukun. The study on the impact effects of margin trading on stock market: Evidence and enlightenments from Taiwan stock market in China[J]. Journal of Finance and Economics, 2008, (10): 99-109. (in Chinese)

[9]许红伟, 陈 欣. 我国推出融资融券交易促进了标的股票的定价效率吗?——基于双重差分模型的实证研究[J]. 管理世界, 2012, (5): 52-61. Xu Hongwei, Chen Xin. Does the pricing of underlying stocks are more efficient after margin trading in Chinese stock market [J]. Management World, 2012, (5): 52-61. (in Chinese)

[10]万迪昉, 李佳岚, 葛 星. 融资融券能否提高交易所自律监管效率?[J]. 证券市场导报, 2012, (8): 66-71. Wan Difang, Li Jialan, Ge Xing. Can margin trading increase the efficiency of self-regulation of stock market exchange?[J]. Securities Market Herald, 2012, (8): 66-71. (in Chinese)

[11]International Monetary Fund. EU commission consultation on short selling[R]. http://www .imf.org/external/np/eur/2010/pdf/080510.pdf, 2010.8.

[12]Miller E M. Risk, uncertainty, and divergence of opinion[J]. Journal of Finance, 1977, 32(4): 1151-1168.

[13]Diamond D W, Verrecchia R E. Constraints on short-selling and asset price adjustment to private information[J]. Journal of Financial Economics, 1987, 18(2): 277-311.

[14]Hong H, Stein J C. Differences of opinion, short-sales constraints, and market crashes[J]. Review of Financial Studies, 2003, 16(2): 487-525.

[15]Bai Y, Chang E C, Wang J. Asset prices under short-sale constraints[R]. Working Paper, Cambriolge: MIT, 2006.

[16]Chang E C, Cheng J W, Yu Y. Short-sales constraints and price discovery: Evidence from the Hong Kong market[J]. Journal of Finance, 2007, 62(5): 2097-2121.

[17]廖士光, 杨朝军. 卖空交易机制、 波动性和流动性——一个基于香港股市的经验研究[J]. 管理世界, 2005, (12): 6-13. Liao Shiguang, Yang Chaojun. The short selling mechanism, the market fluctuation, and the market fluidity[J]. Management World, 2005, (12): 6-13. (in Chinese)

[18]廖士光, 杨朝军. 卖空交易机制对股价的影响——来自台湾股市的经验证据[J]. 金融研究, 2005, (10): 131-140. Liao Shiguang, Yang Chaojun. The impact of short-selling mechanism on stock price: Evidence from Taiwan stock market[J]. Journal of Financial Research, 2005, (10): 131-140. (in Chinese)

[19]Bohl M T, Essid B, Siklos P L. Do short selling restrictions destabilize stock markets? Lessons from Taiwan[J]. The Quarterly Review of Economics and Finance, 2012, 52(2): 198-206.

[20]Devaney M. Financial crisis, REIT short-sell restrictions and event induced volatility[J]. The Quarterly Review of Economics and Finance, 2012, 52(2): 219-226.

[21]Hansen B E. Autoregressive conditional density estimation[J]. International Economic Review, 1994, 35(3): 705-730.

[22]Harvey C R, Siddique A. Autoregressive conditional skewness[J]. Journal of Financial & Quantitative Analysis, 1999, 34(4): 465-487.

[23]Leon A, Rubio G, Serna G. Autoregressive conditional volatility, skewness and kurtosis[J]. The Quarterly Review of Economics and Finance, 2005, 45(4-5): 599-618.

[24]许启发, 张世英. 多元条件高阶矩波动性建模[J]. 系统工程学报, 2007, 22(1): 1-8. Xu Qifa, Zhang Shiying. Multivariate conditional higher moments volatility modeling[J]. Journal of Systems Engineering, 2007, 22(1): 1-8. (in Chinese)

[25]王 鹏. 基于时变高阶矩波动模型的VaR与ES度量[J]. 管理科学学报, 2013, 16(2): 33-45. Wang Peng. Calculating VaR and ES based on volatility models with time-varying higher-moments[J]. Journal of Management Sciences in China, 2013, 16(2): 33-45. (in Chinese)

[26]Nelson D B. Conditional heteroskedasticity in asset returns: A new approach[J]. Econometrica, 1991, 59(2): 347-370.

[27]Engle R F, Ng V K. Measuring and testing the impact of news on volatility[J]. Journal of Finance, 1993, 48(5): 1749-1778.

Margin trading and the stability of stock market: A dynamic perspective

LIUYe,FANGLi-bing*,LIDong-xin,LIXin-dan

School of Management and Engineering, Nanjing University, Nanjing 210093, China

A new model called Threshold Auto-Regressive Conditional Density model with exogenous shocks (abbreviated to be TARCD-X) is developed in the present work. The advantage of this model is that it accommodates all twelve relationships between the four types of information shocks and three indicators of market stability. Therefore, the model can be well employed to investigate the impact of margin trading on the stability of stock market from a dynamic perspective. The shocks include the increase and decrease of stock market price, and trading volume. The indicators of market stability involve volatility, the asymmetry of large up and down movements, and the frequency of large movements of the stock market. The empirical results documented that: (1) eleven of the twelve relationships do not worsen except for the decreasing of trading volume hasa larger effect on conditional volatility after the execution of margin trading; (2) the changes in the margin trading account, as a new information shock, do not increase the volatility or the frequency of large movements, but are significantly correlated to the asymmetry of large up or down movement. This evidence is beneficial to building early warning indicators to identify large movement of stock market.

margin trading; market stability; short sale; conditional density

2013-07-31；

2015-10-28.

国家自然科学基金重点资助项目(70932003)； 国家自然科学基金资助项目(71173098)； 国家自然科学基金青年资助项目(71203091； 71401071)； 教育部人文社会科学研究青年项目(14YJC790025)； 江苏省自然科学基金青年资助项目(BK20130589).

方立兵(1980—)， 男， 安徽舒城人， 博士， 讲师. Email： lbfang@nju.edu.cn

F830.91

A

1007-9807(2016)01-0102-15