金融资产风险度量及其在风险投资中的应用
——基于稳定分布的新视角
耿志祥, 费为银
(1. 北京大学经济学院, 北京 100871; 2. 安徽工程大学金融工程系, 芜湖 241000)
金融资产风险度量及其在风险投资中的应用
——基于稳定分布的新视角
耿志祥1, 费为银2
(1. 北京大学经济学院, 北京 100871; 2. 安徽工程大学金融工程系, 芜湖 241000)
引入稳定分布对沪深两市指数数据进行检验,结果表明两指数具有“尖峰厚尾”的分形特征,在此基础上建立了DaR类风险测度,实证研究表明两指数跌幅时间序列存在协同跌幅共线性效应.其次,给出了蒙特卡洛稳定分布和正态分布模拟下的两类风险测度估计值,建立了离差率模型,结果表明稳定分布下的风险度量适合投资者进行风险管理.最后,研究了不同跟踪时间窗口下的风险测度指标MDD.投资者和风险管理人员不仅要关注VaR类风险,更要警惕DaR类风险指标.
稳定分布; VaR类和DaR类风险测度;离差率模型; 蒙特卡洛模拟; 风险投资
0 引 言
金融市场中充斥着大量的风险,随着金融市场全球化趋势加强和衍生品市场的飞速发展,金融市场呈现出前所未有的波动性,再加上不断的金融创新,金融机构和投资者面临日趋增多且复杂的金融风险,市场中由于风险管理不善造成的损失或公司倒闭的例子不胜枚举.如2007年由美国次贷危机引发美国投资银行的崩溃就是风险管理不到位的结果,先后造成了华尔街的五大投行相继破产,最终酿成了全球性的金融危机.因此,对于金融机构、投资者、风险监管机构乃至政府而言,加强对风险的测度和预防管理刻不容缓.
金融资产的风险测度是金融市场风险管理的基础与核心,一直倍受风险研究人员和投资管理人士的关注,他们都在为寻找合适的度量风险工具而不懈努力.早在20世纪50年代,Markowitz[1]就提出了均值-方差模型,用收益率的方差来描述证券投资风险.由于方差具有良好的统计性质,且度量风险简便易行,因此在投资管理中得到了广泛应用.但随着实证研究的深入,不少学者发现收益率并不服从正态分布,而是存在“尖峰厚尾”的分形特征,一般还带有一定的偏度和位置参数的变化.Ararwal等[2]就认为均值-方差模型低估了尾部风险.1994年,J. P. Morgan在风险度量中引入了VaR(value at risk,风险价值),得到了学术界和实务界的广泛认可,美国的众多评级公司和证券交易委员会都宣布和支持VaR作为风险测度和管理风险的主要方法,巴塞尔银行监管委员会和美国联邦储备银行委员会也认可把VaR作为可接受的金融风险度量方法之一.但随着研究的深入,VaR却受到了众多人士的批评,因为它不满足一致相容性风险度量条件,不能度量尾部风险,更谈不上度量极端事件发生的风险.Artzner等[3]引入了CVaR(conditional value at risk,条件风险价值)作为风险度量工具,能够弥补VaR以上缺点,它满足一致相容性风险度量条件,能够度量尾部发生的风险.Rockafellar 和 Uryasevb[4]认为CVaR比VaR更好地度量金融市场风险,CVaR满足次可数可加性,能够度量超过VaR部分的风险,能够通过线性规划解决大规模的资产组合优化的有效边界问题.但当投资组合损失的密度函数不是连续函数时,CVaR也不再是一致性风险度量模型.在此基础上,Tasche[5]提出了ES(expected shortfall,期望损失)模型,ES模型是对CVaR模型的改进,是一致性风险度量,当损失密度函数连续时,ES模型的结果与CVaR模型得到的结果相同.当损失分布不连续时,两者计算的结果有一定的差异.ES模型对损失的分布没有特殊的要求,分布函数不论在连续还是不连续时,它都能满足一致性风险度量条件.因此,它在度量极端风险模型中得到了广泛的应用.
上面的VaR、CVaR和ES可统称为VaR类风险度量模型.对于投资人员来说,在风险管理中不仅要关注VaR类风险指标,还要注意到投资过程中的风险变化,如证券投资中一次较大的跌幅可能会使投资者的投资策略发生改变.最近,流行于欧美市场的一种新的风险测度方法—MDD(maximum drawdown, 最大跌幅)、AvDD(average drawdown,平均跌幅)、DaR(drawdown at risk,风险跌幅)和CDaR(conditional drawdown at risk,条件风险跌幅)受到了实务人员的追捧*Harmantzis等[6]对DaR类风险度量给出了具体的数学表达式和意义说明,后面DaR类风险度量模型部分会介绍..私人投资者、机构投资者、基金经理、共同基金和对冲基金管理者都开始关注此指标,它们可作为VaR类风险度量的补充,统称为DaR类风险模型.MDD是最大跌幅,它由Acar 和 James[7]首次提出,它是指在某一段时间内,某项资产或资产组合价格从最高点跌到最低点的幅度,通常用百分比表示.Magdon等[8-9]对MDD作了详尽的描述并研究了布朗运动下的MDD. Pospisil等[10]首先在Black-Scholes公式的框架下推导了MDD下的价格扩散方程,通过求解偏微分方程数值解得到了MDD的期望值.Jan Vecer在其工作论文中认为资产组合投资经理可以把MDD当作对冲工具来阻止资产组合投资损失*具体可参见哥伦比亚大学统计系Jan Vecer (2007)的工作论文‘Preventing Portfolio Losses by Hedging Maximum Drawdown’..在国外市场中,资产经理、机构投资者、私人投资者、共同基金和对冲基金越来越关注MDD,这项指标可作为投资的参考指标.例如,假设有两种基金A和B,每种基金账户的开始额度都是1 000万元人民币,在某一个结算日,A基金已达到2 000万元,这时候收益率为100%.另外一个基金B,开始账户也是1 000万元人民币,与A基金的结算日期相同,最后基金也达到2 000万元.但从开始到最后结算这一时间段内,B基金由1 000万元变动3 000万元,然后又跌到1 500万元,最后涨到2 000万元,虽然收益率也是100%,但中间经历了一次较大的跌幅,跌幅达到50%,这对基金管理人员是不得不考虑的风险.因为对于基金经理来说,维护现有客户和开发新的客户是基金能够维持和不断成长的关键所在,尤其对于一个正在上扬的市场或牛市,B基金的跌幅可能引发一部分客户撤离该基金,转投A基金或其它投资.因此,对于基金经理来说,该风险应纳入到日常的风险管理中*在欧美市场,基金经理有时将MDD作为约束条件来进行组合投资优化和风险管理..在我国的香港市场,已经有一些实务人员关注MDD,而内地关注度较少,对MDD研究在学术界还没有完全展开.DaR表示处在风险中的跌幅,简称为风险跌幅.CDaR表示条件风险跌幅.Chekhlov等[11]首次引入了DaR和CDaR风险度量方法进行资产组合投资管理.DaR定义如同VaR,而CDaR则与CVaR和ES相类似,它也满足一致性风险度量条件.Chekhlov等[12]用风险度量指标DD(Drawdown,跌幅)和MDD对资产投资进行组合优化,研究了带有跌幅约束下的最优资产组合最优化模型.Burghardt等[13]研究了DD的分布,并讨论了跟踪时间长度、收益率均值和收益率的波动率对DD分布的影响.Johansen等[14]运用扩展的指数分布对不同国家指数、商品和货币建立了跌幅的严重程度影响模型.Melo等[15]建议用EVT(extreme value theory,极值理论)来分析MDD影响的严重性和持久性,并给出了GARCH波动率与MDD之间的变化关系.
以上学者对风险度量的研究都有一个共同的特点,那就是对金融资产的风险度量通常先假设收益率的分布,如均值-方差模型假设收益率服从正态分布,从微观到现在的宏观风险测度通常都假设资产价格运动服从正态分布⑤宫晓琳[16]在其《未定权益方法与中国宏观金融风险的测度》中假设资产价值的波动遵循几何布朗运动,在求解财务危机发生概率中假设资产服从标准正态分布以及引用的Black-Scholes-Merton期权定价理论也是假设资产收益率服从正态分布得到低等索取权波动率与资产波动率之间的关系式..但正态分布不能描述资产的“尖峰厚尾”现象和分布不对称特征.Mandelbrot[17-18]认为股票收益率可以用特征指数小于2的稳定-列维或稳定-帕累托分布描述收益率的“尖峰厚尾”现象.由于稳定分布没有显示表达式,只能通过特征函数的形式表示,且求解也较为复杂,国内有些学者主要运用稳定分布研究一些指数是否符合该分布,如上证综指和深圳成指等.徐龙炳[19]用Nolan教授提供的稳定分布软件对1993年-2000年沪深两市的股票收益率进行了拟合,得到了稳定分布的参数估计值.黄登仕[20]在金融市场的标度理论中对有关Lévy稳定分布的一些进展进行了评述.郭亚军等[21]引入稳定分布对群组评价方法的研究中得到了群体M的群体偏好在适当长期内具有稳定分布特征,而国内学者对稳定分布应用到投资管理过程中的风险度量非常之少.耿志祥等[22]对上证综指用各种参数分布和非参数分布拟合,建立相关指标结果表明在1%和5%的置信度水平下,稳定分布更适合度量风险,在此基础上建立了DaR类风险度量.本文将选取沪深两市指数日数据对此进行更深入研究.
本文的主要贡献有三个方面.首先,对上证综指和深圳成指运用稳定分布拟合其收益率分布,得到了不同指数的稳定分布参数估计值,对拟合效果进行了拟合效果检验,结果表明稳定分布能够很好的拟合收益率分布.其次,在不同置信度水平下进行VaR类风险和DaR类风险测度研究,得到了上证综指和深圳成指跌幅趋势图,给出了收益率和跌幅相关性分析,这为研究其他金融资产风险度量提供了一种可行方案.最后,通过蒙特卡洛稳定分布和正态分布模拟VaR类和DaR类风险测度,建立了离差率模型,结果表明在风险投资中稳定分布可用于风险管理.对于不同期限的投资,作者研究了不同跟踪时间窗口下的MDD,这也是长短期投资者在投资风险过程管理中更感兴趣的指标,投资者和风险管理人员在投资和风险管理过程中应警惕MDD风险.运用稳定分布这一厚尾分布去管理投资风险可起到控制风险作用.投资者可利用稳定分布对其投资进行风险测度和风险管理.
1 稳定分布、VaR类和DaR类风险测度
1.1 稳定分布
稳定分布又被称为阿尔法-稳定分布(Alpha-stable distribution)或分形分布(Mandelbrot[17-18]),该分布的性质最早由Lévy推导出来的,而他的工作是建立在Pareto研究有关收入分布的基础上,所以也称之为稳定帕累托分布.Pareto研究发现,占个人收入为97%的收入分布近似为对数正态分布,而对于其余3%的分布却产生异常现象,有较厚的尾部.Mandelbrot首次提出股票收益率服从稳定分布,其分布在均值处有尖峰,有较厚的尾部,此分布由非线性随机过程产生一种具有自相似性和长期记忆的特征.稳定分布有若干种参数化的形式⑥可参考Nolan[23] 给出的Alpha-stable分布(简称为稳定分布)的几种定义、3种参数化形式和一些性质,Nolan教授提供的稳定分布软件可以计算出四个参数估计值和每个估计值的置信区间,稳定分布软件可在其主页链接的页面上下载,有具体的使用说明..这里使用常用于计算与分析的0-参数化特征函数定义,在此参数化下的参数都有直观的意义.大多数稳定分布都没有显示表达式,只能通过特征函数的形式表示.随机变量X被称为稳定分布当且仅当它的特征函数由下式表示
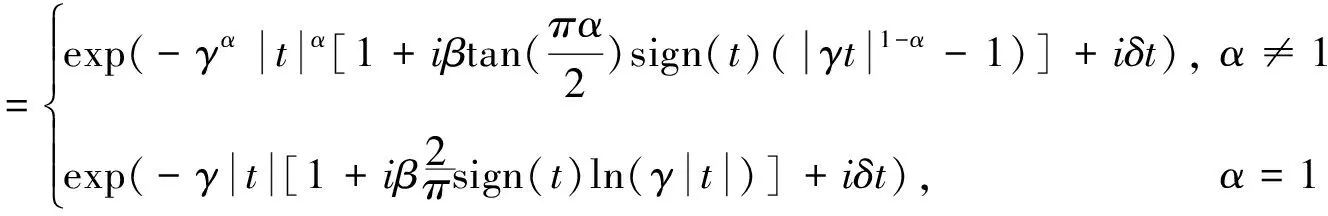
(1)
其中0<α≤2,-1≤β≤1.sign(t)是如下的符号函数
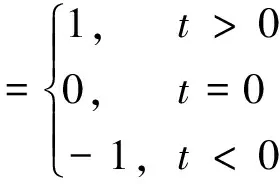
(2)
当γ=1,δ=0时,X~S(α,β,1,0;0)被称之为服从标准稳定分布,这时可简写为X~S(α,β; 0).
从以上的定义中可知,稳定分布有四个参数α,β,γ,δ. 其中α是特征指数,0<α≤2,它是稳定分布最重要的参数,用来刻画尖峰厚尾的程度,α越小,分布的峰部越尖,尾部越厚.α=2时,变为正态分布;β是偏度参数,-1≤β≤1, 它反映了分布的峰值偏离位置参数的方向.β=0时,分布是对称的;β>0时,分布向右偏;β<0时,分布向左偏.β和α共同决定了稳定分布的形状;γ是尺度参数.γ≥0,也可理解为分散程度系数,它描述了概率分布的分散程度.γ越小,分布在对称中心附近集中程度越高;δ是位置参数.-∞<δ<+∞,它表示分布中心对x轴中心的位置,δ>0表示分布偏向x轴的正半轴,δ<0表示分布偏向于x轴的负半轴.
大多数稳定分布的密度函数没有显式,有三种特殊的稳定分布可以写出其密度函数,它们分别是正态分布、柯西分布和列维分布.
1)正态分布或高斯分布.X~N(μ,σ2),其密度函数形式如下
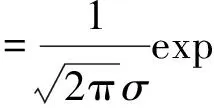
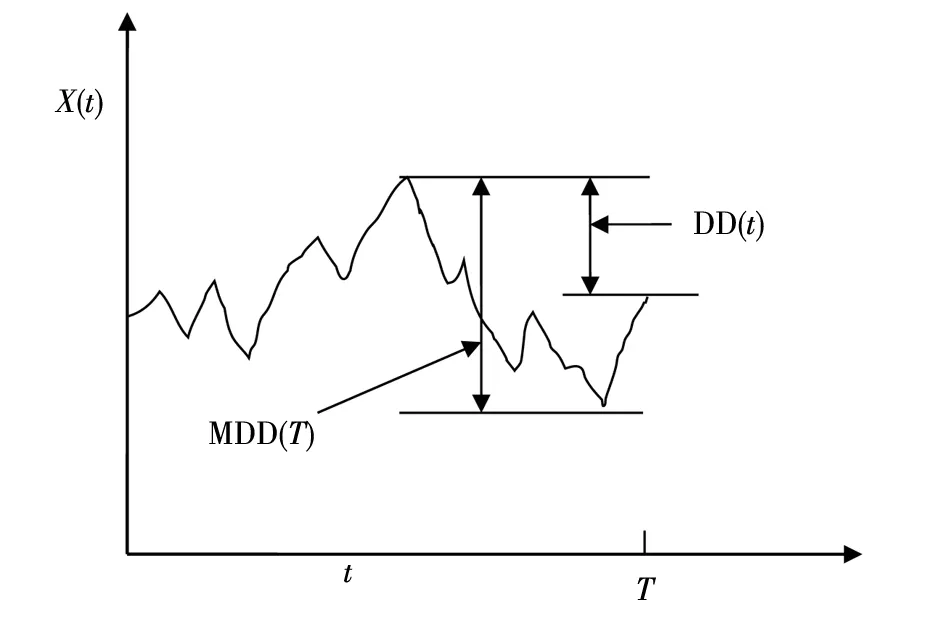
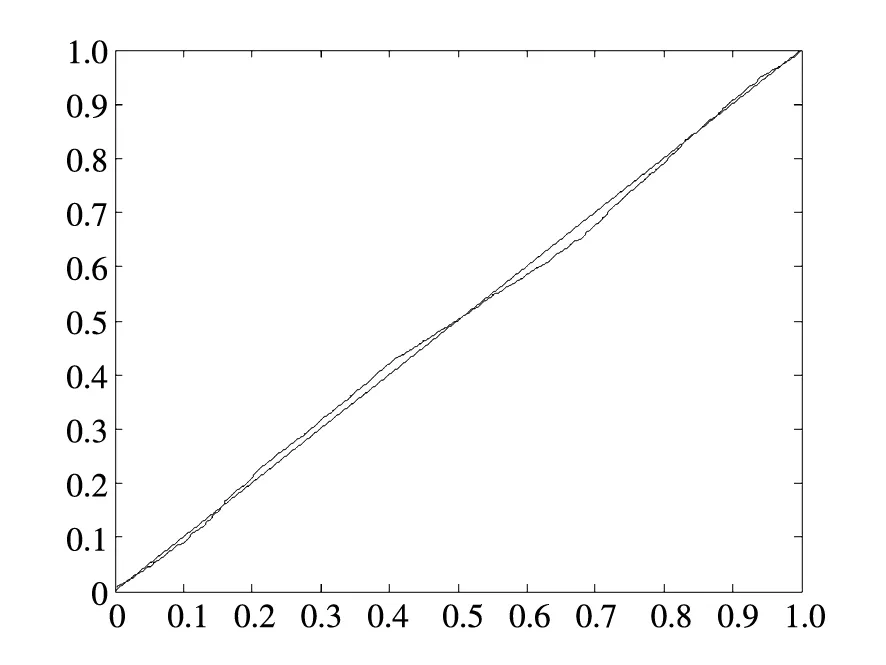
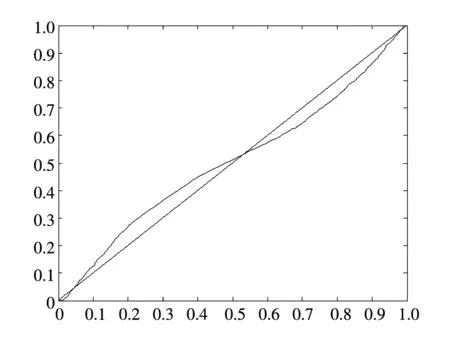
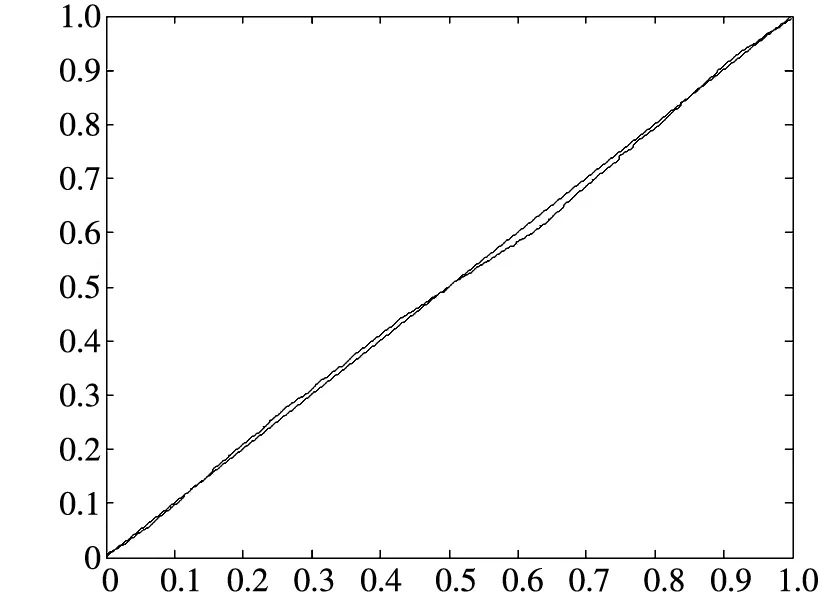
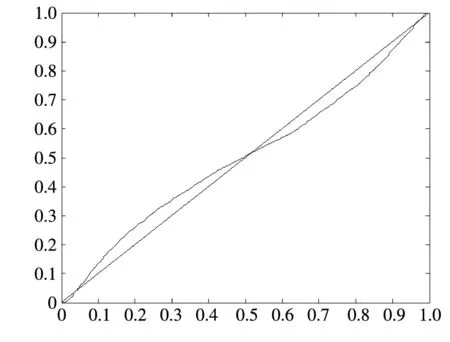
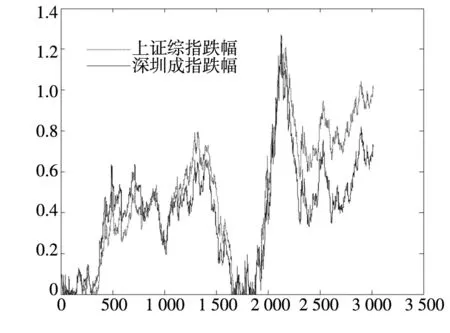
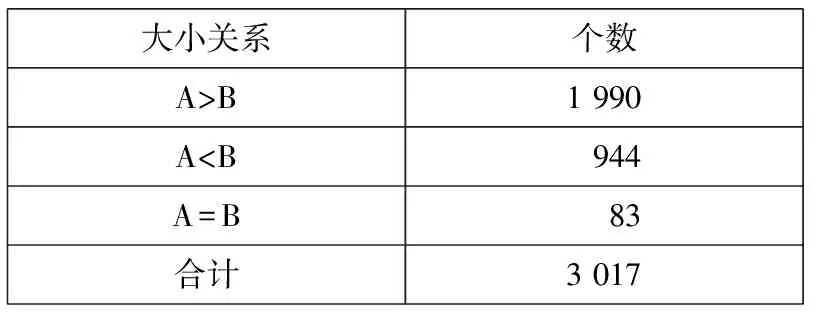
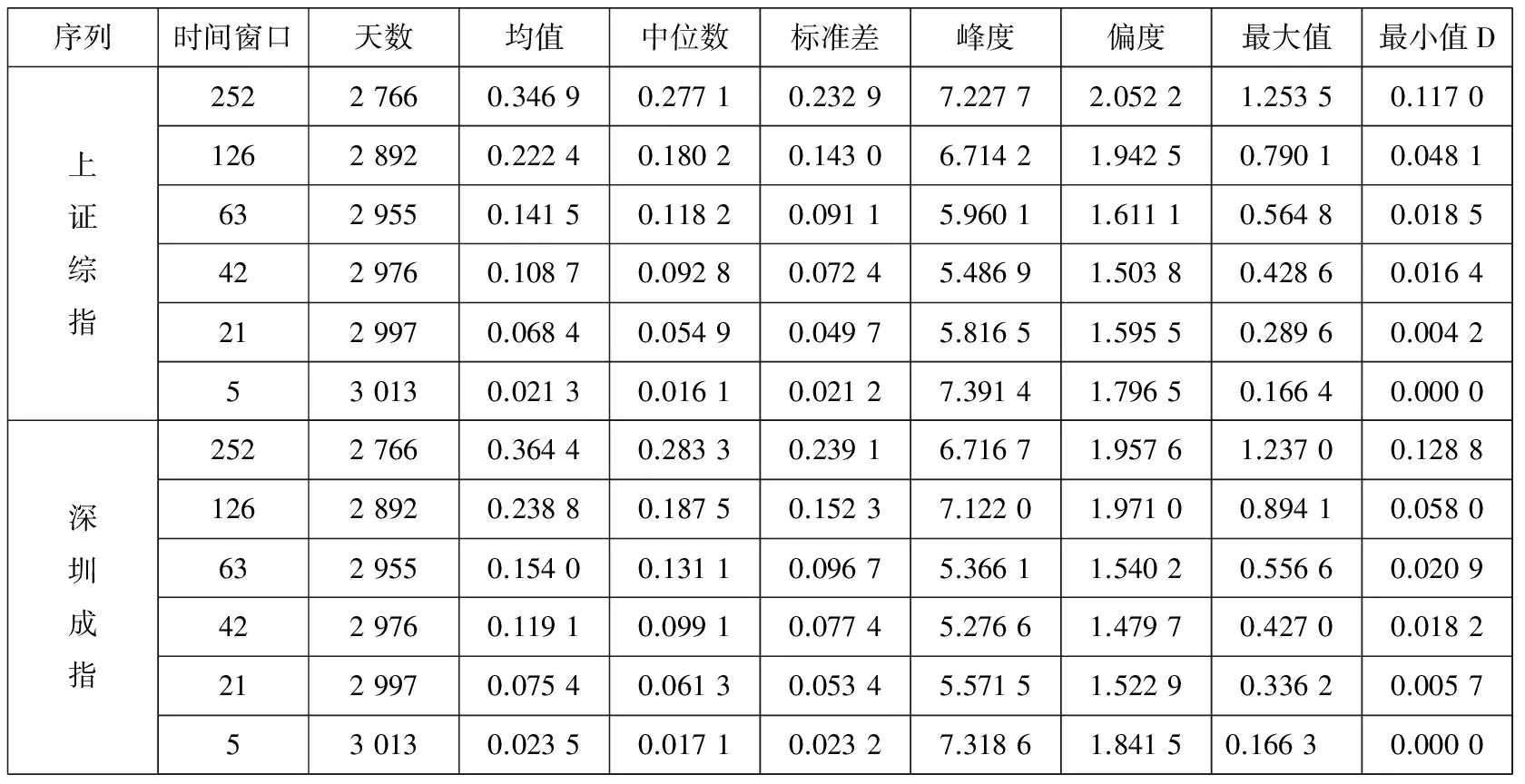
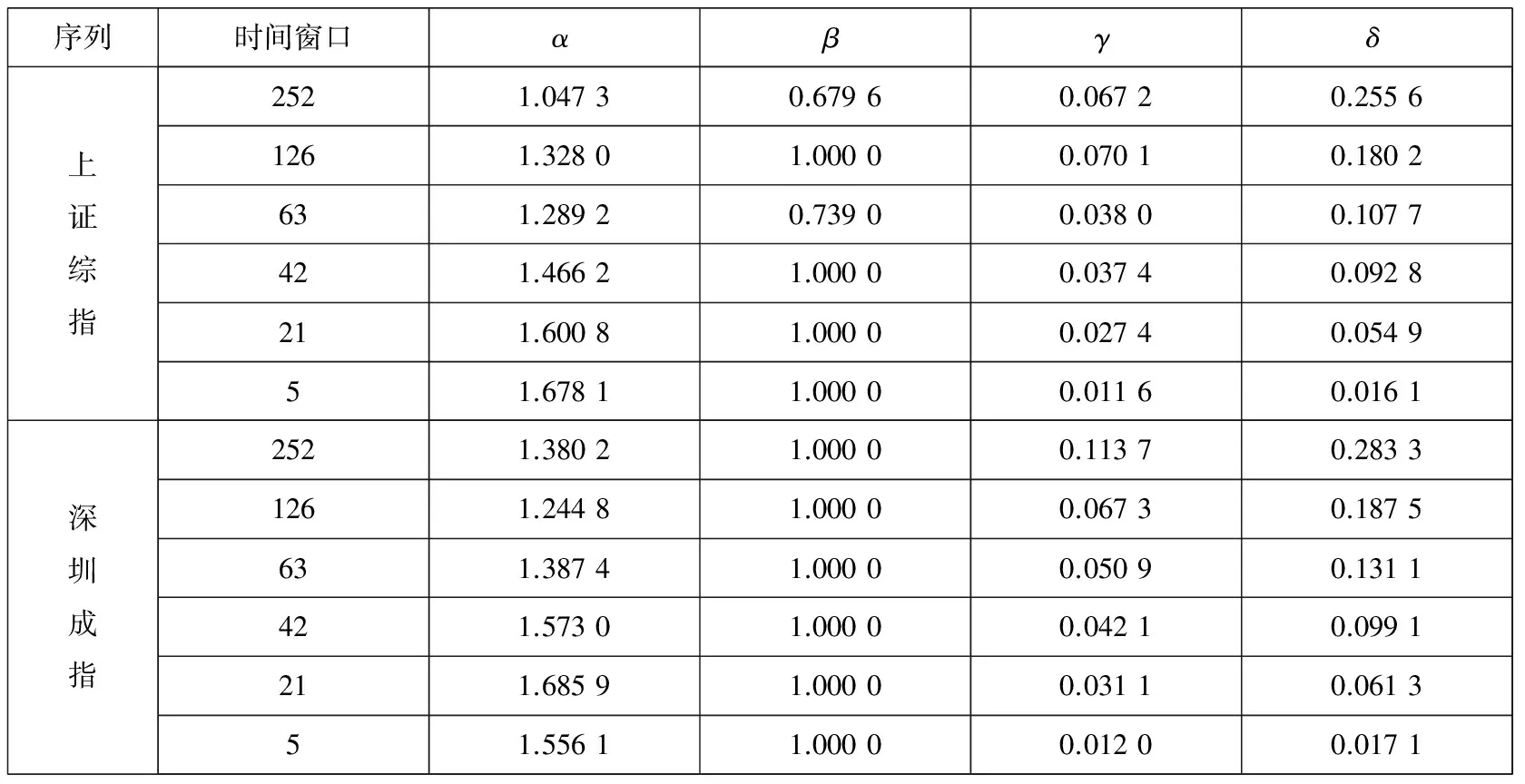
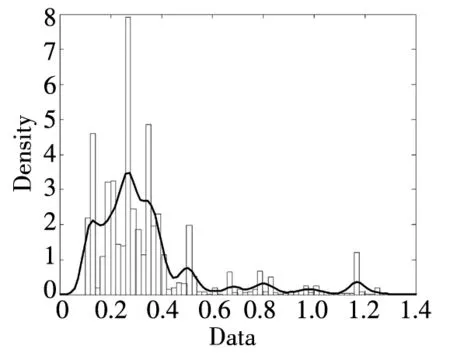
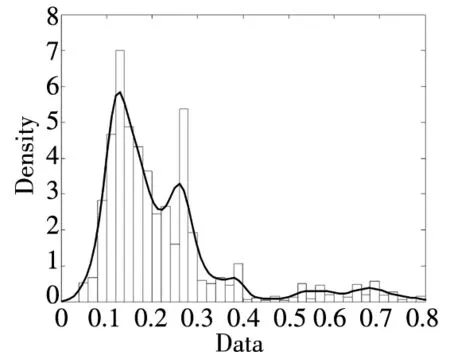
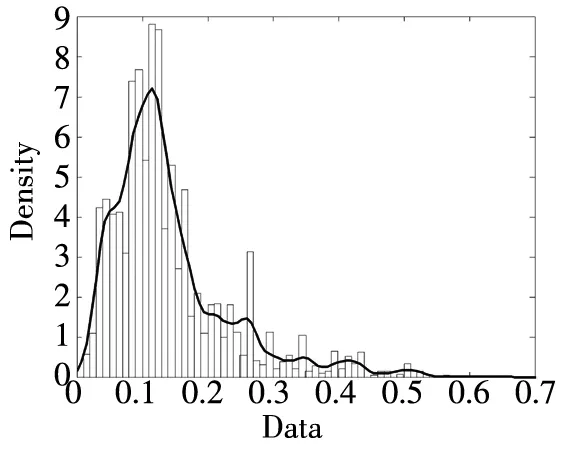
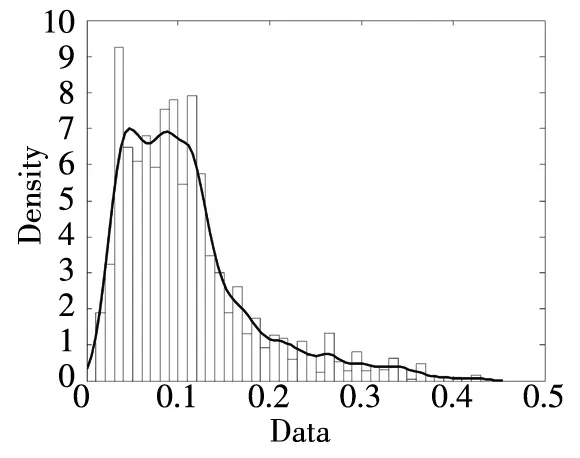
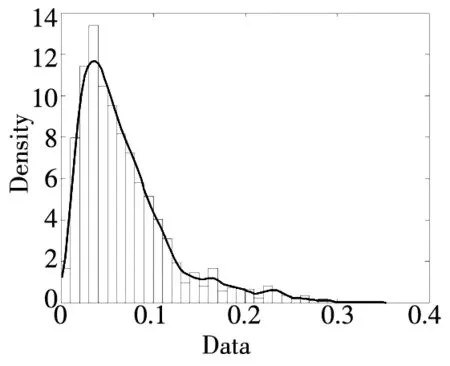
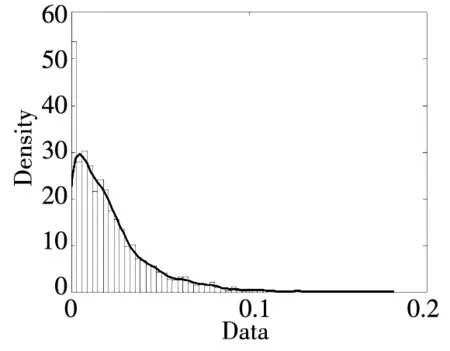
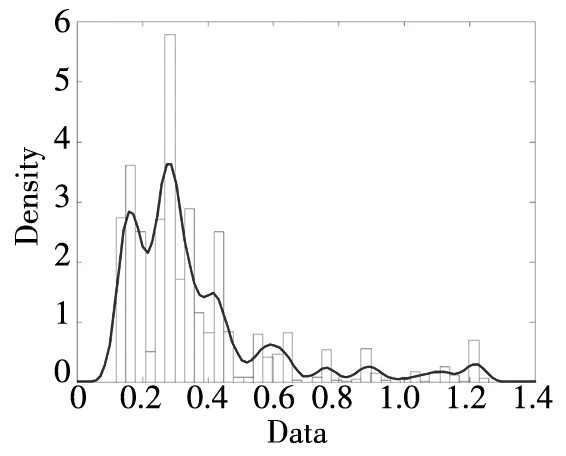
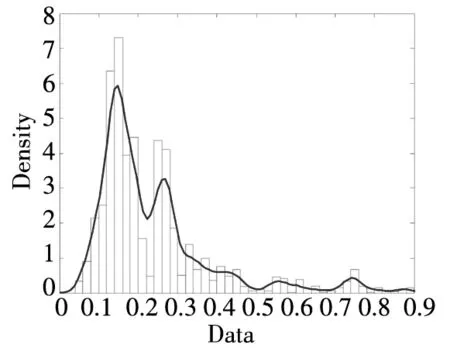
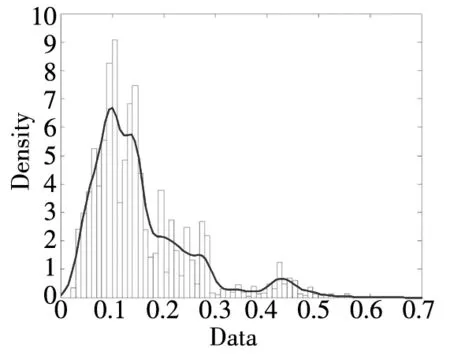
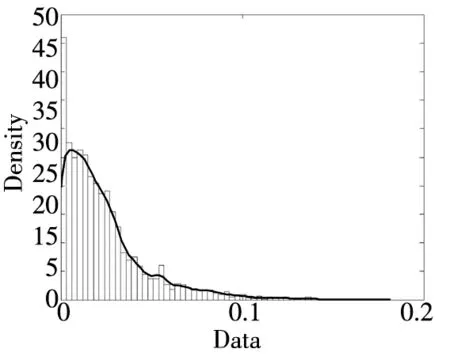
-∞ (3) 根据文献[23],可以计算出正态分布的参数为α=2,β=0. 2)柯西分布.X~Cauchy(γ,δ),其密度函数形式如下 -∞ (4) 在物理学中,此分布也被称作为Lorentz分布.同样可以计算它的参数为α=1,β=0. 3)列维分布.X~Le′vy(γ,δ),其密度函数形式如下 δ (5) 1.2 VaR类风险测度 VaR类风险测度包括不同置信度水平下的VaR和CVaR测度.VaR表示处在风险中的价值,简称风险价值.它表示在正常的市场条件下和一定的置信度水平下,某资产或投资组合预期可能遭受的最大损失.给定随机变量X,其置信度水平为α下的VaR定义如下 VaRα(X)=-qα(X)=-inf{x∶P[X≤x]≥α} (6) 由于VaR不满足一致性风险度量条件,且不能度量尾部风险和极端事件的发生.CVaR可以克服以上缺点,其定义由下式给出 CVaRα(X)=-E[X≤qα(x)] (7) 这里X是连续性随机变量,其定义和性质可参看文献[3].CVaR考虑了超过VaR值损失的测度,有效地改善了VaR处理后尾部分损失的问题,它满足一致性风险度量条件.但当X不是连续性随机变量时,CVaR不满足一致性风险度量条件,需要对其改进.ES模型正是对CVaR的改进,具体定义和性质可参考Tasche[5].当X是连续性随机变量时,ES和CVaR计算值相同;当X不是连续性随机变量时,两者计算值有一定的差异*不少专家和学者认为ES和CVaR是同一个度量的两种表示,但在资产价格不连续时,两者计算有一定的差异,且在不连续时,ES是对CVaR的修正,是一致性风险度量,而CVaR则不满足.. 1.3 DaR类风险测度 在讨论DaR和CDaR之前,先给出跌幅的数学表达式. (8) DD(t)代表资产在时间t之前的峰值到目前t时刻的跌幅或损失,其中X(t)是直到t时刻的累积收益率.此时MDD就可以定义为如下表达式. (9) 图1展示了DD(t)和MDD(T)的度量,DD(t)是资产价格到T时刻的跌幅,MDD(T)则是时间[0,T]上的最大跌幅. 图1 跌幅与最大跌幅 (10) 其中α是置信度水平,CDaR表示超过DaR下(1-α)*100%的损失的期望*在实证研究部分将取置信度水平为95%和99%..AvDD的表达式如下 (11) 它表示[0,T]内的平均损失或跌幅,它可以看作是置信度水平为0时的CDaR值*平均跌幅在实务中运用较少,一般关注MDD较多,MDD与DaR和CDaR经常被用于最优投资组合策略分析和风险约束指标..MDD是置信度水平为1时的CDaR值.因此,MDD和AvDD正好是CDaR的两种端点值. 2.1 数据来源和稳定分布检验分析 本文选取2000年1月4日至2012年6月29日的上证综指和深圳成指的每日收盘价为原始数据,每种指数都有3 018个收盘价数据,数据来源于财汇金融分析平台.它们的收益率取对数收益率,即rt=ln(pt)-ln(pt-1),pt是第t天的收盘价,pt-1是前一天的收盘价.为了叙述方便,以下将对数收益率简称为收益率*对数收益率有一些良好的性质,计算累积收益率时,各对数的直接相加化简后是某个区间上的收益率,在收益率数值r很小时,近似有ln(1+r)=r.本部分使用的软件是STABLE (John. P. Nolan提供)、Matlab和Eviews 6.0..两种指数样本收益率的基本统计特征见表1. 表1 收益率样本的基本统计特 表1中两指数都有较高的峰度,异于正态分布峰度值3,且上证综指比深圳成指有稍高的峰度,也就是有较厚的尾部,且都有较小的负偏性,深圳成指负偏程度较大.深圳成指的标准差大于上证综指,这表明其波动性较强,因为标准差既含有负的波动,也含有正的波动,所以很难从标准差的角度分析两指数的风险性.从J-B统计量来看,两者都拒绝正态分布,都有“尖峰厚尾”特征.进一步可通过Kolmogorov-Smirnov检验,结果都拒绝正态分布假设.为了更好地刻画收益率的分布,不仅要考虑它的对称性和分散度,还要考虑其“尖峰厚尾”性.因此,用前面介绍的稳定分布来拟合收益率分布*利用STABLE软件中第1个选项:极大似然估计法来计算收益率的各参数估计值.. 表2 收益率的稳定分布参数估计结果 表2中上证综指的特征指数(1.482 7)小于深圳成指的特征指数(1.536 1),即上证综指比深圳成指有较尖的峰部和较厚的尾部,两种指数分布都异于正态分布特征指数2,显示两市场的分形特征,这与有效市场假设(EMH)矛盾,实际市场呈现分形市场(FMH)特征,这与Mandelbrot研究大多数金融时间序列呈现分形特征相吻合.曹宏铎[24]研究证券市场复杂行为分形标度与机会决策研究时,以中国深市为研究对象,研究发现中国证券市场存在相关性,表现为分形时间序列,其行为不符合布朗(BM)运动,而是分形布朗运动(FBM),并在心理学框架下运用时变Hurst指数揭示了市场的易变行为、均值回复和长期相关性.不同时间尺度上的价格变动存在某种统计上的自相似性,收益率之间并非独立,而是存在非线性相关.上证综指的α值越小表示其收益率分布的尾部越厚,收益的状态持续性越强,在预测大盘趋势时信息显得更重要.与之相反,深圳成指特征指数α较大,股票的日收益之间的独立性较前者更大,收益长期记忆特性越小,股票价格波动随机性较大,从而预测难度加大.从偏度角度出发,可知两指数偏度都小于0,显示负偏状态,这说明两指数正负变化较频繁,稳定性较差,风险较大.上证综指的负偏程度较大也说明了信息是以非线性的方式传递,人们接受信息的过程需要时间差,以非线性的方式作出反应,市场价格不能完全反映所得的信息,投资方式显示非理性,这可以用正反馈交易策略效应来解释.市场波动受投资者情绪的影响,使得股票价格运动并非像有效市场假设的随机游动,而是呈现出有偏的随机游动.李红权等[25-26]采用非线性动力学分析股市波动的本质特征与形成机制,结果表明股票市场存在低维混沌现象,具有内生的不稳定性.他们得到的结论是实际的金融时间序列服从一个有偏的随机游走过程.以上的拟合结果也验证了这一结论.两市场指数收益率具有显著的分形特征与长记忆效应,其价格过程表现为非线性动力学价格行为. 通过两指数收益率的正态分布和稳定分布的P-P图,可以看出稳定分布拟合的效果较佳*Q-Q图有时在尾部不稳定,P-P图检验比Q-Q图检验更加稳定..图2、3、4和5中可以看出两指数稳定分布拟合的直线与y=x最接近,近似共线性.而正态分布拟合效果较差. 图2 上证综指稳定分布P-P图 Fig. 2P-PplotofAlpha-stabledistributionforShanghaicompositeindex 图3 上证综指正态分布P-P图 图4 深圳成指稳定分布P-P图 图5 深圳成指正态分布P-P图 2.2 VaR类和DaR类风险测度结果与分析 上证综指和深圳成指收益率分布的确定为其风险测度奠定了基础.两指数各有3 018个收盘价数据,转化为对数收益率后有3 017个,利用式(8)可以求出两指数的跌幅时间序列,将两跌幅序列画在同一个坐标系中有如下图6. 图6 上证综指和深圳成指跌幅(DD(t))趋势图 图6中可以看出两指数的跌幅趋势图基本一致,上升和下降的过程基本上保持一致,且大约在1 600到1 800之间跌幅基本在0附近,这期间最稳定.随后经历一个大幅攀升过程,跌幅不断增大,两市风险达到前所未有的风险状态.经过计算,风险的开始日期都为2007年10月17日,最后两指数都在2008年11月4日达到最大跌幅*Matlab中较容易计算得到最大跌幅的天数,再返回具体日期..这段时间恰好是美国的次贷危机对中国股市逐渐影响到2008年金融危机爆发这段时间.结果造成上证综指MDD为127.24%,深圳成指MDD为123.70%,随后跌幅下降一定的幅度后呈现徘徊震荡阶段,从最大跌幅后可以从图形上看出上证综指的跌幅都超过深圳成指,趋势仍然保持一致,两种指数跌幅可近似为循环“N”强度减弱至稳定型向前推进. 表3 跌幅DD(t)的基本统计特征 表3清晰地描述了沪深指数的跌幅性质,上证综指的最大跌幅MDD为1.272 4,大于深圳成指最大跌幅*Harmantzis等[6]选取的8种指数中,除NASDAQ(MDD为1.511)和DAX(MDD为1.298)外,其它6种指数的MDD都小于上证综指和深圳成指的MDD,其中包括香港恒生指数(HIS)MDD为0.918.由于选择时间不同可能造成结果的差异,以后可选择同样时间窗口进行比较研究..通过两指数标准差可知,上证综指跌幅的波动性较强,跌幅风险较大,这与图5中观察到的结论一致.深圳成指的峰度为3.08,可近似认为跌幅服从正态分布,符合有效市场假设(EMH).上证综指跌幅仍然不满足EMH,DD(t)的分布有较薄的尾部和平坦的峰部,这也反映了上证综指发生较大跌幅的概率较大,跌幅存在较长的时间,股市风险较高.这可能由于投资于上海市场的投资者投资情绪波动较大有关,他们对信息反应的异质性程度较高,可能不少投资者是噪音交易者,追涨杀跌的现象时有发生.而深圳市场由于离香港市场较近,而香港金融市场发展具有较长的历史,成熟度较高,部分投资者可能在两地之间投资或受香港投资者影响,表现的相对趋于理性. 从分析可知,两指数跌幅既有高度相关性,也存在细微差异.从相关性的角度分析,通过计算得到两指数收益率的相关性系数为0.938 8,跌幅的相关性系数为0.924 2.这表明两指数有很强的协同收益和协同跌幅效应. 表4 上证综指和深圳成指DD(t)统计量关系 注:A代表上证综指跌幅;B代表深圳成指跌幅. 显然,表4中上证综指的跌幅个数有近66%大于深圳成指,这为投资沪深两市的投资者提供了跌幅参考数据,也可以利用此方法比较其它不同市场之间的跌幅统计关系,从而作出有利的投资选择. 在讨论了两指数跌幅的关系后,现在对两指数进行风险测度,两指数时间跨度仍为2000年1月4日至2012年6月29日,使用经验数据(历史数据)计算两指数的各种风险测度值. 表5 基于经验数据(历史数据)的各种风险测度估计结果 注: 表中VaR类风险度量结果中的负号表示损失.第一行中的95和99代表置信度水平,如DaR95表示在给定的经验数据下,处在 风险中的跌幅在置信度水平为95%下的最大跌幅不会超过1.166 7(对上证综指而言),以下类同. 从DaR类风险测度来看,表5中上证综指跌幅类风险测度值都大于深圳成指,而VaR类值则相反.也就是说,从VaR类风险测度的角度而言,上证综指的风险小于深圳成指;从DaR类风险测度的角度而言,上证综指的跌幅风险大于深圳成指.这与表4中得到的结果一致,两指数的VaR类和DaR类风险测度变化方向不一致,呈现相反的趋势.上证综指不稳定性较高,而深圳成指发生亏损的极端事件的概率较高*两指数的VaR类和DaR类风险测度变化方向相反,这与Harmantzis等[6]的部分结果一致,如CAC与HIS两类风险测度的变化方向.而多数情况下两类风险变化的方向是一致的,也就是说,一个指数的VaR类风险较大,则DaR类风险也较大,如DAX与CAC,NASDAQ与S&P等,详见参考其计算结果..两个市场投资者的结构差异以及异质程度可对此解释,正如前面分析,香港市场对深圳市场的投资者影响多于上海市场而造成了市场反应程度一定的差异有关.上海市场受投资者情绪影响较大,深圳市场虽波动也较大,但相对趋于理性,从而造成了DaR类和VaR类风险的差异.投资者在投资过程中应学会理性对待自己的投资行为,金融监管部门应重视机制的设计与完善,加强投资风险的教育和防范,查处市场的违规操作和内幕交易,降低市场非正常的波动,从而营造一个公平、透明和健康的市场氛围. 为了进行跌幅的预测和风险管理,采取不同的分布去度量风险并与经验值比较,从而找到合适的分布去度量和管理风险.利用表2中求出的两指数收益率稳定分布参数结果,采用蒙特卡洛稳定分布模拟产生上证综指和深圳成指收益率随机变量,产生随机点的个数为两指数的收益率个数,即3 017个.产生随机变量的方法见Chambers等[27],模拟次数为10 000次,再经过计算可以得到稳定分布下的各种风险测度结果. 同样,采用蒙特卡洛正态分布模拟产生上证综指和深圳成指收益率随机变量,这时两指数的均值和标准差采用表2中的位置参数和尺度参数估计值,特征指数为2,模拟次数同样是10 000次,各种风险测度结果见表7. 表6 蒙特卡洛稳定分布模拟下的各种风险测度估计结果 表7 蒙特卡洛正态分布模拟下的各种风险测度估计结果 表6和表7中的风险测度结果是经过蒙特卡洛模拟10 000次,经过计算再取平均值的结果. 2.3 离差率模型 由以上离差率表达式,可以得到稳定分布和正态分布下的各种风险测度离差率,见表8和表9. 表8 蒙特卡洛稳定分布模拟下的风险测度估计结果离差率 表9 蒙特卡洛正态分布模拟下的风险测度估计结果离差率 从表8中可知,稳定分布下的风险测度都是正值,这表明稳定分布收益率模型总是高估了风险.而表9中正态分布下的风险测度结果都为负值,这表明正态分布假设低估了风险,且低估的程度较大,其离差率的绝对值都大于20%.对于上证综指,DaR类风险度量的低估程度超过了50%,最高的AvDD达到了76.51%,而VaR类风险度量低估程度都超过了40%(VaR95除外).与上证综指风险度量程度相比,深圳成指的低估程度较轻,但多数都超过了30%,最高ES99达到了46.64%.显然,对于投资者而言,利用正态分布管理风险严重低估了尾部风险,难以达到风险管理的目的. 稳定分布高估了风险,但程度较轻,稳定分布下大多数离差率的绝对值小于正态分布相对应的离差率绝对值.上证综指的高估程度要比深圳成指的程度要轻,上证综指的VaR99、ES95和ES99较大,最高ES99达到73.07%,这说明两指数极端事件发生的概率较大,有较厚的尾部.深圳成指的DaR类风险度量值都大于上证综指(AvDD除外).从VaR95值来看,两指数在稳定分布下的风险度量值与经验度量值最为接近,离差率仅为1.5%和0.35%,这对于利用稳定分布进行VaR95管理风险最为适合,是较为稳健的风险测度,金融资产发生极端事件的风险可以用稳定分布来度量.对于风险规避者,他们往往更倾向于高估风险,而不是低估风险,也就是说,与正态分布相比,他们更喜欢用稳定分布来风险测度和风险管理,实证研究表明稳定分布假设是一种较为准确和保守的风险度量. 2.4 不同跟踪时间窗口下的MDD 投资者在投资中往往更加关注某个窗口时间内的MDD,而不是整个5年或10年时间甚至更长的时间.对于投资者而言,他们通常更关注短期收益和跌幅,如一个星期、一个月、一个季度、半年或一年内的最大跌幅究竟有多大,从历史数据出发,建立样本内MDD模型,通过统计推断来预测MDD未来发展趋势.由于沪深股市的交易特点,经过逐年统计可知每年可交易的时间大约为252天,半年约为126天,一个季度约为63天,一个月约为21天,而每周可交易的时间为5天(周末休市,遇到节假日则可能没有5天,基本上都为5天)*这里跟踪时间窗口的方法为:如两指数一年(252天)交易时间,第1个MDD的计算应选择从第1个收益率到第252个,第2个MDD则从第2个收益率到第253个,依次类推,总共有2 766个MDD.其它不同跟踪窗口时间的MDD可类似得到.. 表10 不同跟踪时间窗口(单位:天)下的MDD统计特征 表11 不同跟踪时间窗口下的MDD稳定分布估计值 表10给出了不同时间窗口下的最大跌幅统计特征.例如,当时间窗口为5天时(一周),基于历史数据的上证综指在过去的所有周交易数据中*这里的历史数据是指2000年1月4日至2012年6月29日期间发生的对数收益率数据,共有3 017个.,最大跌幅的一周跌幅为16.64%,最小跌幅为0(指数一周持平或上涨),而相对应的深圳成指分别为16.63%和0.随着时间窗口的减小,除峰度和偏度外,两指数的其它统计量也都随之减小,而峰度和偏度呈现无规则的变化,这与Harmantzis[6]所研究的8种指数的规则变化有所不同*8种指数的峰度和偏度随着时间窗口的减小而增加..这可能跟沪深股市自身所具有的特点相关.如沪深股市出现频繁和大幅度的跳跃行为,与市场突发信息密切相关,左浩苗等[28]研究了中国股市的跳跃风险度量行为.这种不规则的变化凸显了我国股市作为“新兴股市”不够成熟的一面*李红权,洪永淼,汪寿阳[29]在《我国A股市场与美股、港股的互动关系研究:基于信息溢出视角》中得出我国A股市场不论在危机发生前还是在金融危机期间,其波动性是最高的.详见其实证分析部分..表11是对应不同跟踪时间窗口下的MDD稳定分布估计值,特征指数和偏度参数同样呈现不规则变化,上证综指在一年(交易天数为252)和一个季度(交易天数为63)MDD稳定分布估计偏度参数分别为0.679 6和0.739 0,其它时间窗口偏度参数都为1(包括深圳成指全为1),完全右偏. 图7和图8是两指数不同时间窗口下的MDD核密度图.两指数在不同跟踪时间窗口下的核密度曲线相近,差异较小,联动性较强,但其变化不规则.上证综指在跟踪时间窗口为5天时,MDD特征指数α达到最大(1.678 1),而深圳成指则在跟踪时间窗口为21天时,MDD特征指数α达到最大(1.685 9).核密度图也有所反映这一现象*在正常的条件下,一般由中心极限定理可知,随着独立同分布样本数的增加,正态化趋势应增加,而沪深两指数有变异现象,在跟踪时间窗口越小时,正态化趋势却没有显现的那么吻合.. 252天 126天 63天 42天 21天 5天 图7 上证综指不同跟踪时间窗口下的MDD核密度图 Fig. 7 Kernel density diagrams of Shanghai composite index under different tracking timeT 252天 126天 63天 42天 21天 5天 图8 深圳成指不同跟踪时间窗口下的MDD核密度图 Fig.8 Kernel density diagrams of Shenzhen component index under different tracking timeT 本文首先研究上证综指和深圳成指的厚尾分布,引入稳定分布对两指数的对数收益率分布进行拟合,利用STABLE软件中的极大似然估计得到了两指数的稳定分布参数,结果表明两指数存在“尖峰厚尾”的分形特征,那么基于有效市场的传统理论假设,如金融价格序列服从正态分布、随机游走和独立性假设就会受到质疑,它们已经不能准确地刻画资本资产的动态价格行为.进一步通过P-P图检验验证两指数收益率服从稳定分布,而正态分布拟合效果较差.这也说明了实际的金融市场是一类复杂的非线性动力学系统,存在分形和混沌现象,股票价格行为服从分数布朗运动.在此基础上,重点介绍目前流行于欧美市场的一种流行的风险测度——DaR类风险测度.选取2000年1月4日至2012年6月29日最新的上证综指和深圳成指的每日收盘价为原始数据,得到了两指数的跌幅趋势图,通过跌幅趋势图发现一路攀升的跌幅时间段都为2007年10月17日到2008年11月4日,联动性强,这正是美国次贷危机爆发逐渐影响中国到爆发全球性的金融危机阶段,在2008年11月4日两市达到最大跌幅,上证综指MDD为127.24%,深圳成指MDD为123.70%.后经过国内的一系列刺激政策和投资者信心的增长,经济逐渐复苏和增长预期的形成,跌幅才有所缓和,且之后上证综指的跌幅一直大于深圳成指的跌幅,其跌幅趋势都可近似为循环“N”强度减弱至稳定型向前推进. 通过两指数跌幅相关性分析,得到两指数跌幅的相关性系数达到0.924 2,收益率相关系数为0.938 8,有很强的趋势共线性,即协同收益和协同跌幅效应共线性.实证研究还表明上证综指跌幅有近66%大于其深圳成指跌幅.本文重点研究了两指数的VaR类和DaR类风险测度.利用蒙特卡洛稳定分布模拟和蒙特卡洛正态分布模拟两指数收益率随机变量,模拟次数为10 000次,其风险测度结果取平均值.为了比较不同结果的效果,通过定义离差率分析了不同分布下的风险测度估计值与经验数据风险测度值的高低估程度,结果表明稳定分布高估了风险,且程度较轻.而正态分布低估风险的程度较大,这对于风险测度和投资者风险管理而言,根本起不到未来管理风险的目标.对于风险规避者而言,稳定分布是较为理想的选择方式,稳定分布下的风险测度是一种更为准确和保守的风险度量.最后,为了模型更加具有应用价值,本文给出了不同跟踪时间窗口下的MDD结果,这为投资者和风险管理者提供了短期关注MDD的方法,从而在短期中可以预防和管理MDD风险. 本文的重点给出了现在流行于欧美市场的一种新的风险测度方法——DaR类风险测度,并用稳定分布这一符合实际的金融资产分布去度量DaR类风险.它和VaR类风险测度共同成为投资者关注的指标,它们之间有很高的相关度,在某些情况下,投资者可以通过控制DaR类来减少VaR类风险,因此不少投资者更加关注DaR类指标.在欧美市场和我国的香港金融市场,私人投资者、机构投资者、基金经理、共同基金和对冲基金管理者都开始关注此指标.就拿MDD来说,它表示最大累计跌幅.对于基金管理人员,它反映了基金过去曾经在高位跌至低位的幅度,在前面的分析中得知波动率不代表风险,而MDD的好处是能够清晰地看出损失(跌幅)的多少,能够反映其风险.再者,它提供了另外一条线索,如果跌幅较大,则返回原先状态的难度增大,甚至不可逆转,这对投资者来说尤为重要.例如,经过一段相同的时间后,投资者1投资的基金跌幅10%,则要返回原先的水平需要升幅约11%.投资者2投资的基金跌幅25%,则要返回其原先水平需要升幅约33%.投资者3投资的基金跌幅为50%,则返回原先水平需要升幅100%.显然跌幅越大,基金返回原先水平的难度越大.因此,投资者和风险管理人员更要警惕MDD指标.对于DaR和CDaR,它们类似于VaR和CVaR,CDaR和CVaR都是一致性风险测度,DaR类风险测度针对跌幅,而VaR类风险测度则针对收益率. 上证综指的跌幅类风险测度值大于对应的深圳成指跌幅类风险值,而深圳成指的VaR类风险测度值大于相应的上证综指跌幅类风险.结果还表明两市的不稳定性,以及跌幅序列变化的联动性.作为投资者和风险管理人员,应认识到利用正态分布去进行投资风险管理往往难以达到风险管理的目标,甚至由于低估风险而带来灾难性的后果.应注意到金融资产分布的厚尾性,如采用稳定分布进行两类风险测度与预防管理风险,不仅要关注VaR类风险,更要关注过程管理风险中的DaR类风险,投资者应警惕DaR类风险,保守型投资者可采用稳定分布对其投资进行风险测度和风险管理.在投资过程中,当然也可以利用DaR类指标来进行组合投资优化.此外,研究结果表明资本市场存在分形和混沌现象,股票价格行为具有非线性动力学的复杂演变特征,而不是经典金融理论所假设的随机游走和有效市场假说,实际金融系统的复杂性决定了整个金融系统往往以非线性方式对外界信息或冲击做出反应,这为研究与理解资本市场的复杂性提供了新的思路和方向,也必将为投资行为、金融实践和金融监管产生深远的影响. [1]Markowitz H. Portfolio selection[J]. The Journal of Finance, 1952, 7(1): 77-91. [2]Ararwal V, Naik N Y. Risks and portfolio decisions involving hedge funds[J]. The Review of Financial Studies, 2004, 17(1): 63-98. [3]Artzner P, Delbaen F, Eber J M, et al. Coherent measures of risk[J]. Mathematical Finance, 1999, 9(3): 203-228. [4]Rockafellar T, Uryasevb D. Conditional Value-at-Risk for general loss distributions[J]. Journal of Banking and Finance, 2002, 26(7): 1443-1471. [5]Tasche D. Expected shortfall and beyond[J]. Journal of Banking and Finance, 2002, 26(7): 1519-1533. [6]Harmantzis F, Miao L. On the impact of heavy tails returns to popular risk measures: Evidence from global indices[R]. Working Paper, 2005, Available at SSRN: http://ssrn.com/abstract=744567. [7]Acar E, James S. Maximum loss and maximum drawdown in financial markets[C]//Forecasting Financial Markets Conference, London, 1997. [8]Magdon-Ismail M, Atiya A. Maximum drawdown[J]. The Journal of Risk, 2004, 17(10): 99-102. [9]Magdon-Ismail M, Atiya A, Pratap A, et al. On the maximum drawdown of a brownian motion[J]. Journal of Applied Probability, 2004, 41(1): 147-161. [10]Pospisil L, Vecer J. PDE methods for the maximum drawdown[R]. Working Paper, New York: Columbia University, 2007.[11]Chekhlov A, Uryasev S, Zabarankin M. Portfolio optimization with drawdown constraints[R]. Research Report, Florida: University of Florida, 2000. [12]Chekhlov A, Uryasey S, Zabarankin M. Drawdown measure in portfolio optimization[J]. International Journal of Theoretical and Applied Finance, 2005, 8(1): 13-58. [13]Burghardt G, Duncan R , Liu L. Understanding drawdowns[R]. Working Paper, New Jersey: John Eiley and Sons Ltd., 2003. [14]JohansenA, Sornetrte D. Large stock market price drawdowns are outliers[J]. Journal of Risk, 2000, 4(2): 69-110. [15]Melo Mendes, De B V, Camara Leal R P. Maximum drawdown: Models and applications[R]. Working Paper, Federal University at Rio de Janeiro, 2004. [16]宫晓琳. 未定权益分析方法与中国宏观金融风险的测度分析[J]. 经济研究, 2012, (3): 76-87. Gong Xiaolin. Measuring and analyzing China’s macro-financial risk with CCA approach[J]. Economic Research Journal, 2012, (3): 76-87. (in Chinese) [17]Mandelbrot B. Paretian distributions and income maximization[J]. Quarterly Journal of Economics, 1962, 76(1): 57-85. [18]Mandelbrot B. The variation of certain speculative prices[J]. The Journal of Business, 1963, 36(4): 394-419. [19]徐龙炳. 中国股票市场股票收益率稳态特性的实证研究[J]. 金融研究, 2001, (6): 36-43. Xu Longbing. The empirical study of steady returns in Chinese stock markets[J]. Journal of Financial Research, 2001, (6): 36-43. (in Chinese) [20]黄登仕. 金融市场的标度理论[J]. 管理科学学报, 2000, 3(2): 27-33. Huang Dengshi. Scaling and scale invariance in financial markets[J]. Journal of Management Sciences in China, 2000, 3(2): 27-33. (in Chinese) [21]郭亚军, 侯 芳. 面向评价局部环境的导向性群组评价方法研究[J]. 管理科学学报, 2013, 16(2): 12-21. Guo Yajun, Hou Fang. Oriented group evaluation method for partial evaluation environment[J]. Journal of Management Sciences in China, 2013, 16(2): 12-21. (in Chinese) [22]耿志祥, 王传玉, 林建忠. 金融资产厚尾分布及常用的风险度量[J]. 数量经济技术经济研究, 2013, 30(2): 49-64. Geng Zhixiang, Wang Chuanyu, Lin Jianzhong. Heavy tailed distributions of financial assets and popular risk measures[J]. Journal of Quantitative and Technical Economics. 2013, 30(2): 49-64. (in Chinese) [23]Nolan J P. Stable Distributions: Models for Heavy Tailed Data[M]. Boston: Birkhauser, 2012. [24]曹宏铎. 证券市场复杂行为分形标度分析与机会决策研究[J]. 金融研究, 2005, (1): 138-145. Cao Hongduo. The analysis of complex behavior fractal index and research on investment decision[J]. Journal of Financial Research, 2005, (1): 138-145. (in Chinese) [25]李红权, 马超群, 邹 琳. 中国证券市场的混沌动力学特征研究[J]. 中国管理科学, 2005, 13(专辑). Li Hongquan, Ma Chaoqun, Zou Lin. Research on chaotic dynamic characteristics in China stock market[J]. Chinese Journal of Management Science, 2005, 13(Special issue). (in Chinese) [26]李红权, 汪寿阳, 马超群. 股价波动的本质特征是什么?—基于非线性动力学分析视角的研究[J]. 中国管理科学, 2008, (5): 1-8. Li Hongquan, Wang Shouyang, Ma Chaoqun. What’s the nature of volatility in stock prices-based on the nonlinear dynamical analysis principle[J]. Chinese Journal of Management Science, 2008, (5): 1-8. (in Chinese) [27]Chambers J M, Mallows C L, Stuck B W. A method for simulating stable random variables[J]. Journal of the American Statistical Association, 1976, 71(354): 340-344. [28]左浩苗, 刘振涛. 跳跃风险度量及其在风险—收益关系检验中的应用[J]. 金融研究, 2011, (10): 170-184. Zuo Haomiao, Liu Zhentao. Jump risk measurement and its application in the test of the relationship between risk and return[J]. Journal of Financial Research, 2011, (10): 170-184. (in Chinese) [29]李红权, 洪永淼, 汪寿阳. 我国A股市场与美股、港股的互动关系研究: 基于信息溢出视角[J]. 经济研究, 2011, (8): 15-37. Li Hongquan, Hong Yongmiao, Wang Shouyang. Information spillover among China’s A-shares market, US stock market and HK stock market[J]. Economic Research Journal, 2011, (8): 15-37. (in Chinese) Risk measures of financial assets and its application in risk investment: From the new perspective of stable distribution GENGZhi-xiang1,FEIWei-yin2 1. School of Economics, Peking University, Beijing 100871, China; 2. Department of Financial Engineering, Anhui Polytechnic University, Wuhu 241000, China The paper uses the Alpha-stable distribution to examine the data of Shanghai composite index and Shenzhen component index. The results show that both of them have the fractal characteristic of “leptokurtic and heavy tails”. We establish DaR-type risk measures. The empirical study demonstrates that series between the two indexes have collinearity to some extent in terms of drawdown. Furthermore, using the Alpha-stable parameters of the two indexes, we give the VaR-type and DaR-type risk measures estimation in the Monte Carlo Alpha-stable and normal simulations, and we construct the model of bias. Finally, this paper emphasizes on MDD with different tracking time. As investors and risk managers, we should focus on not only VaR-type risk measures, but also DaR-type risk indexes. Alpha-stable distribution; VaR-type and DaR-type risk measures; bias model; Monte Carlo simulation; risk investment 2013-05-18; 2015-10-26. 国家自然科学基金资助项目(71171003; 71571001). 耿志祥(1981—), 男, 安徽芜湖人, 博士生. Email: zhixianggeng@sohu.com F830.9 A 1007-9807(2016)01-0087-15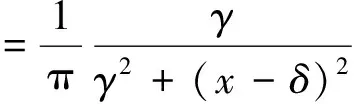
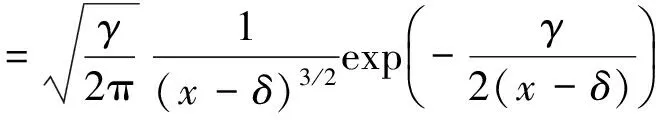
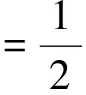
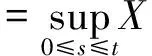
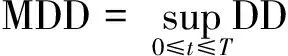
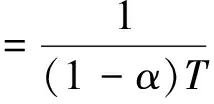
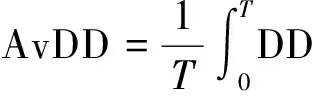
2 实证研究与结果分析











3 结束语

