基于日度低频价格的波动率预测
刘威仪, 孙便霞, 王明进
(1. 首都经济贸易大学金融学院, 金融风险研究院, 北京 100070; 2. 南方科技大学金融数学与金融工程系, 深圳 518055; 3. 北京大学光华管理学院, 北京 100871)
基于日度低频价格的波动率预测
刘威仪1, 孙便霞2, 王明进3*
(1. 首都经济贸易大学金融学院, 金融风险研究院, 北京 100070; 2. 南方科技大学金融数学与金融工程系, 深圳 518055; 3. 北京大学光华管理学院, 北京 100871)
利用作者提出的GARCH-X的框架,将以往文献中提出的各种基于金融资产的最高、最低、开盘和收盘等低频价格信息的波动率静态估计,统一地扩展成对波动率的动态预测模型.通过对上证指数近十几年数据的实证分析,并借助于对波动率的高频估计和预测评估的一些最新研究成果,本文揭示出合理地利用价格极差及开盘价的信息可以显著地提高对波动率及风险价值的预测能力.
波动率; 风险价值; 极差; GARCH-X模型; 预测
0 引 言
对金融资产价格波动率(volatility)的估计和预测一直以来都是金融计量研究中一个备受关注的问题.在经典的Black-Scholes期权定价模式下,标的资产的价格被设定为服从几何布朗运动,其中的波动率为一个常数,此时大家关注的基本上是一个参数估计的问题,即如何根据观测价格获得对波动率的估计.后来,随着人们对资产价格变化中的“波动簇集”等现象的认识,如何描述波动率的动态规律并对其进行预测成了问题的关键.从上个世纪八十年代开始,各种GARCH类以及随机波动率类的参数模型被提出来并被深入研究,且在风险管理、投资组合以及资产定价等各类金融决策中得以广泛的应用.
近些年来,基于日内高频交易数据的各种对波动率的非参数估计方法又成为了该领域的热点.所谓的高频数据原则上是指记录全部交易过程的数据,实际上的高频数据则多是以分钟或秒为采集频率的交易数据.理论上看,利用高频交易数据可以得到对波动率更加精准的估计,通常称之为已实现波动率(realized volatility, RV)估计[1].然而,实际的高频数据由于受到微观结构噪声等因素的影响,使得直接由高频的原始价格构造出来的RV往往不能给出波动率的相合估计[2].因此,一种策略是选用5min-30min等稍低的采样频率来构造RV,另外的方案则是设法消除微观噪声的影响,其中后者也是近几年此类研究的一个基本方向.
相比上述估计技术上的困难,在具体应用当中,高频交易数据的获取也并不容易,比如一些国内主要金融数据库中的高频数据通常往往只有最近几年的数据,且存在着价格昂贵、数据缺失比较严重等问题.因此,将基于高频数据的波动率估计和预测应用到现实的投资决策中目前还是有诸多的局限性.
从定义上看,波动率是指资产在一个时段内收益率的方差或标准差.回顾早期基于低频信息对波动率估计的文献可以看出,除了利用每天的收盘价格得出日收益率及其对应的样本方差估计之外,在一定的模型假定下,充分利用每天的开盘价、最高价和最低价等公开的低频信息可以得到关于波动率的更加有效的估计.比如,Parkinson[3]利用每天的价格极差(即最高价和最低价的差值)构造出的波动率估计比常规使用日收益率平方得到的估计要有效4.9倍,即后边一个估计的均方误差是前者的4.9倍.而Garman 和 Klass[4]利用最高价、最低价、开盘价和收盘价给出的波动率估计则比使用收益率平方给出的估计要有效8.4倍.如果基于同样的模型设定,假如按照每天连续交易时间4 h计算,那么容易推算出,上述估计的效率与由每28 min采样得出的RV估计的效率是相近的.如此看来,只要充分地利用公开的低频价格信息原则上是可以得出接近由高频数据给出的一些波动率估计的.
当然,上述的结果在理论上仅限于对波动率的静态估计.特别地,无论是Parkinson的估计还是Garman-Klass的估计都是基于对数价格服从无漂移的布朗运动的模型假设.对于各种波动率是动态的模型假定,上述结果的理论基础显然不复存在.因此,在考虑波动率的动态模型时,直接利用Parkinson估计与收益率平方估计的倍数关系并不合适.从这个意义上讲,能够预测每天价格的极差(比如文献[5,6])也并不等同于就能够给出波动率的预测.
为此,文献[7]利用GARCH模型的框架提出了GARCH-R模型,即将价格极差代替收益率的平方嵌入到GARCH模型中,该模型将条件方差表达成过去的价格极差序列的一个线性组合.实证的结果表明了该模型相比传统的GARCH模型无论在对波动率的预测还是进行风险管理等方面都有显著的改善.另外可以参见文献[8]中类似的研究.
本文进一步扩展了文献[7]的思路,主要的贡献体现在如下几个方面: 1)结合Garman和Klass[4]以及Rogers和Satchell[9]等利用开盘价、收盘价、最高价和最低价等低频价格信息给出的对波动率的不同的静态估计形式,进一步提出了GARCH-GK以及GARCH-RS等新的模型形式,并通过实证分析揭示出这些模型在波动率预测和风险管理方面的优势;2)通过上述模型,考察了无交易时段(即下午收盘之后到第二个交易日开盘之前的时段)对预测波动率的影响;3)在进行波动率预测的比较方面采用了此类研究中所提出的一些最新的标准和比较方法[10].
1 对波动率的静态估计
本文将波动率定义为一个时段内资产收益率的方差.在早期的研究当中,往往都假定波动率是一个常数.比如在Black-Scholes的框架下,资产的价格服从几何布朗运动,如果记St为资产价格,且pt=lnSt,那么易知pt服从
dpt=μ*dt+σdWt
(1)

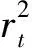
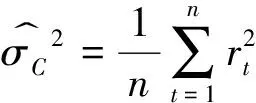
(2)
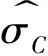


(3)

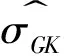
(4)
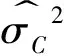
对于Parkinson估计和Garman-Klass估计的应用及各种推广形式的研究一直受到人们的关注,可参见文献[9,12-14]以及文献[15-17]等.
下面给出两种情形下的拓展.

XRS,t=ut(ut-ct)+dt(dt-ct)
(5)
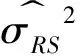
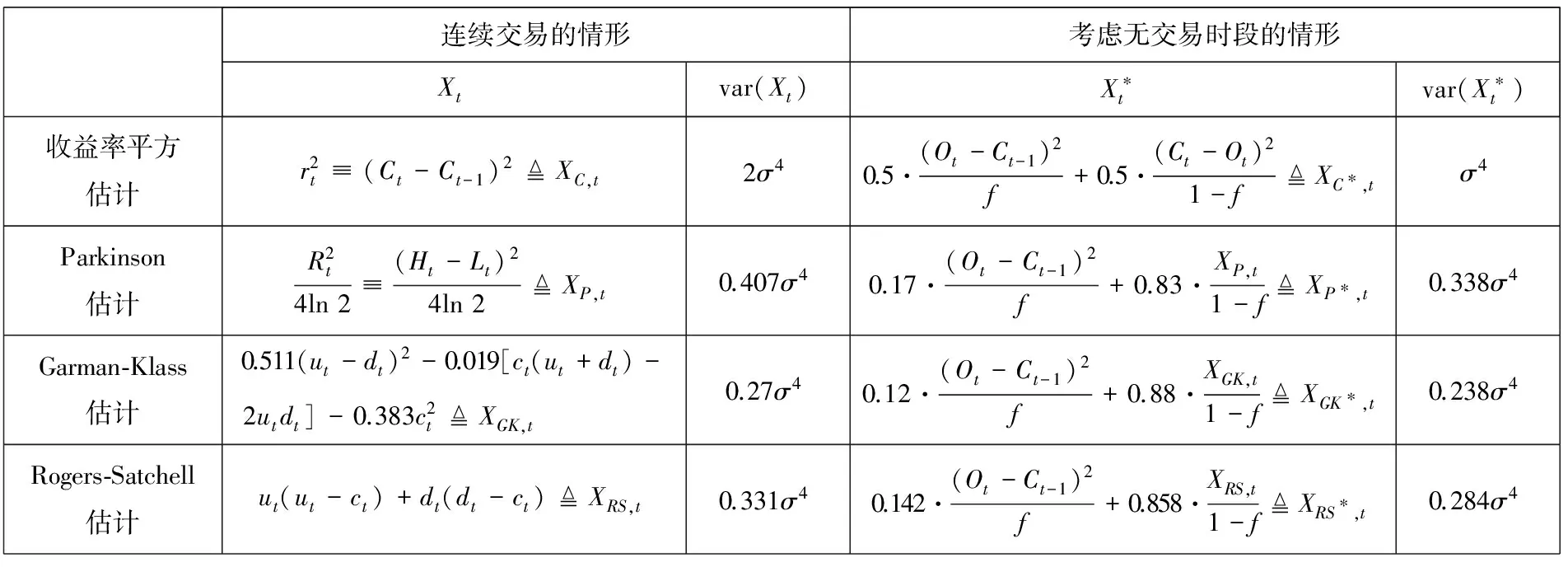
其二,如果考虑一天里无交易的时段,即从上一个交易日的收盘到今天的开盘属于无交易时期,记为[t-1,t-1+f],其中0 图1 无交易时段的示意图 (6) (7) 类似地,可以得到考虑无交易时段加入开盘价信息时式(3)、式(4)、式(5)三种估计的改进形式.为表达简洁起见,将其统一列在表1中.由于此时的开盘价Ot已经有别于前一个交易日的收盘价Ct-1,因此加入这个价格的信息可以进一步增加对波动率估计的精度. 值得特别强调的是,此时由于交易只在[t-1+f,t]的时段内发生,因此观测到的日内最高价Ht和最低价Lt都是就该时段内而言的. rt=σt·at,at~i.i.d.(0,1) (8) 如果将式(1)的价格模型予以推广,假定在给定Ωt-1的条件下,价格服从局部常数的布朗运动,即 dp(t-1+τ)=μtdτ+σtdW(τ),τ≥0 (9) (10) (11) (GARCH-GK模型) (12) (GARCH-RS模型) (13) 而且,为了考虑无交易时段的影响,又可以分别将上述模型(10)-(13)中的XC,t,XP,t,XGK,t,XRS,t分别替换为表1中的XC*,t,XP*,t,XGK*,t,XRS*,t并得到 (GARCH-C*模型) (14) (GARCH-P*模型) (15) (GARCH-GK*模型) (16) (GARCH-RS*模型) (17) 为了统一起见,不妨将式(10)和式(11)分别记作GARCH-C和GARCH-P模型.当然,为了考虑波动率变化中可能的非对称效应,即正负非预期收益率对未来波动率的影响可能存在着区别,可以类似于文献[20]中的设置,在上述式(10)-式(17)中加入非对称的项,从而进一步拓展上述模型.比如,在模型(10)中加入非对称项就是所谓的GJR-GARCH模型,文献[7]也曾考虑了在式(11)中加入非对称项的情形. 如表1所示,在对波动率进行静态估计的时候,Garman-Klass估计相比收益率平方和Parkinson的极差估计更为有效,那么,通过上述的框架将其纳入到波动率的动态预测中是否可以提高预测的效果就是一个值得研究的问题.为此,本文将通过实证的分析来考察和比较上述八种模型在波动率预测中的效果.为了简洁起见,后面的实证分析没有考虑加入非对称项的形式. 为了评价不同模型的预测能力,既可以通过比较它们对波动率本身的预测来进行,也可以结合某种具体的投资决策比如风险管理来比较不同模型的运用效果. 3.1 对波动率的预测 由于真实的波动率是不可观测的,在评价和比较波动率模型时通常要借助真实波动率的一些“代理值”(proxy).比如收益率的平方或者利用高频交易数据构造的各种已实现波动率估计. 但是,代理值和真实值之间的误差可能会使得预测评价出现不可忽视的偏差,甚至出现依据不同的损失函数会挑选出完全不同的“最优”模型[21,22].因此,在评价过程中选择所谓“稳健的(robust)”损失函数就显得尤为重要.稳健性是指当采用一种损失函数来比较两个不同的预测值时,不管是采用代理值还是真实值得到的优劣次序是一致的.除此之外,一个好的损失函数还应该不依赖于预测值和代理值的尺度变化(re-scaling),即如果同时将其乘以某个相同的倍数,不应该影响评价的结果.这样的损失函数被称为满足齐次(homogeneous)条件. 最近,Patton[23]给出了一类同时满足稳健性和齐次性要求的损失函数,具体形式为 (18) 表1 几种不同的低频波动率估计 无交易时段的情形已经不同. 一旦确定了波动率的代理值及损失函数的形式,评价的原理即是比较不同模型样本外(out-of-sample)预测结果的平均损失.考虑到样本选取的随机性,需要针对模型的预期损失进行统计检验.这种检验比较既可以在模型之间两两地进行,也可以同时对几个模型进行多重比较. 所谓的两两比较就是判断比如模型i和模型j对应的预期损失是否存在显著性的差异,即检验假设 H0∶E[dij,t]=0 H1∶E[dij,t]≠0 (19) 相比之下,对模型预测能力的多重比较则是同时针对多个模型之间的比较.本文采用是有控制的多重比较方法,即检验某一个模型(称为参照模型,记为模型0)是否同时都优于另外几个模型k=1,2,…,m,或者说相比其它m个模型,模型0是否具有所谓的超预测能力(superiorpredictionability,SPA).沿用前面的记号,此时需要检验的假设是 (20) 拒绝假设式(20)意味着至少有一个E[d0k,t]>0,即m个模型当中至少有一个的预测效果好于所选定的参照模型.Hanson[25]给出了检验假设式(20)的Bootstrap方法,细节在此从略. 3.2 对风险价值的预测 波动率预测在金融决策中的一个应用就是为了更好地进行风险管理,因此,除了从统计意义上比较不同模型的预测效果之外,下面从风险管理的角度,比较本文的模型对风险价值VaR和条件风险价值CVaR(又称为expected shortfall)的预测效果. VaRα,t+1=μt+1+Zασt+1 (21) 这里的Zα是标准正态分布的α分位数,σt+1就是在t时刻对t+1期波动率的预期值,在本文中由不同的GARCH-X模型产生;此时对应CVaR的预测值则由下式给出 CVaRα,t+1=E[rt+1|rt+1≤VaRα,t+1] (22) 在风险价值的预测评价方面,VaR的预测评价方法已经较为丰富和全面[26-27],而CVaR的预测评价方法则主要是利用损失函数[28].为了统一地评价不同模型对VaR和CVaR的预测效果,本文仍然采用了比较损失函数的方法. 仿照文献[26],对VaR预测的损失函数采用的是 (23) 对于CVaR,一种简单的做法是采用与VaR完全相同的评价形式[29],但严格意义来讲,应该考虑到二者定义上的不同.因此,这里采用了文献[28]给出的对CVaR预测的预测损失函数 (24) 在此基础之上,同样也可以运用Diebold-Mariano检验进行模型的两两比较以及Hansen的SPA检验. 下面以对上证指数日波动率的预测为例来考察和比较第3节中提出的8个GARCH -X模型的预测效果.选取的数据从2000年1月5日到2011年12月30日共有2 900个观测,其中2005年1月4日以后的1 701天的数据作为样本外观测用于比较模型的预测效果.样本外观测每天波动率的代理值通过高频交易数据由两种方法计算得到,一种是所谓的已实现波动率(realized volatility, RV),即将一天里每5 min收益率的平方相加而得;另外一种是已实现极差波动率(realized range volatility, RRV),是将每5min时段内的极差平方除以4ln 2之后求和(参见文献[30,31]等).考虑到极差估计有低估的倾向,这里的RRV采用了与Martins和vanDijk[31]中式(11)一样的调整方法. 需要指出的是,无论是RV还是RRV都是基于交易时段的高频数据得到的,由于每天交易的时段只有四个小时,原则上这里的RV或RRV仍然不能直接作为全天波动率的度量.为此,这里采用了Hansen和Lunde[32]提出的方法将隔夜无交易时段的波动考虑进来,具体来说,就是用下式将RV调整为全天的波动率度量 (25) 其中rON,t表示隔夜收益率,即开盘价与上一个交易日收盘价的对数差值,而ω1和ω2是两个常数,可按照文献[32]中的式(8)计算.尽管文献[32]中还给出了另外两种调整方法,但是按照最近Ahoniemi和Lanne[33]的研究,这种线性组合的调整方法相对更加准确一些.类似地对RRV也用相同的方法调整为全天波动率的度量.这样得到的1 701天的RVa和RRVa序列的相关系数为0.98. 表2 不同模型波动率预测的损失函数平均值比较 注: 1)这里计算损失函数时波动率的代理值采用的均是RVa; 2)第一行的所有X项为GARCH-X模型的简写, 例如C对应的即是 GARCH模型、P对应GARCH-P模型, 具体见式(10)~ 式(17); 3)L1,L2,L3,L4分别为b={1,0,-1,-2}对应的损失函数, 具体见式(18). 预测值序列按照如下的滚动方式产生:首先用2000年1月5日到2004年12月31日的1 199个观测拟合GARCH-X模型并由此给出未来一个交易日(即2005年1月4日)波动率的预测值;然后将拟合模型的窗口向前滚动一天,即用2000年1月6日到2005年1月4日的1 199个观测拟合模型并给出下一个交易日的波动率预测,以此类推,直至得到2011年12月31日的波动率预测.这样最终得到波动率预测值序列包含了1 701个观测. 由各个模型给出的预测值及每天的代理值即可按照式(18)得到每个模型的损失函数序列.表2给出了不同模型损失函数的平均值,其中代理值采用的是RVa.采用RRVa的情形与此类似,不再单独列出. 分析表2的结果可以得到如下的一些认识:1)对于这里展示的几种损失函数而言,七个GARCH-X模型基本上都比GARCH模型(即表2中对应“C”的列)预测效果要好一些,唯一的例外是RS对应的模型,在b取较大值的损失函数时显得比GARCH要弱一些,但对b较小的损失函数,RS的模型也要好于传统的GARCH.总的来看,结合了开盘价、最高价及最低价等低频价格信息的确可以改善只依赖于收盘价格的GARCH模型的预测能力.2)从顺序上看,预测效果最好的模型是由XP*,t及XGK*,t对应的GARCH-X模型,其次是由XP和XRS*对应的模型,由XGK及XC*给出的模型预测效果更弱一些,最后XRS模型的效果比XC对应的模型略微好一些.这与在表1中给出的静态情形下几种估计效率的次序具有一定的相似性,但是并不完全一致.可以认为,将极差的信息纳入动态模型是最重要的.因为不难看出无论是Parkinson的形式还是Garman-Klass的形式里面都直接包含了极差的信息,相比之下,尽管Rogers-Satchell的估计形式当中也利用了最高价和最低价,却只是通过比较它们与开盘价或收盘价的差距来捕捉波动的信息,这可能是导致它在预测效果上差一点的原因.3)表2从第2到第5行拟合模型时误差项采用的是正态分布,下面第6到9行用的则是t分布,结果表明拟合模型时采用不同的误差项分布对于模型的预测效果基本没有产生太大的影响,只是采用正态分布时,P*给出的模型效果最好,而采用t分布时,则是由GK*给出了最好的预测效果. 为了避免抽样的不确定性,可以对几种模型的期望损失进行两两比较推断,即检验假设式(19). 由于对应的情况太多,表3仅给出部分的比较结果. 在表3给出的结果中有两点是明显的,一是除RS之外的六种GARCH-X模型的预测效果好于GARCH模型(C对应的模型)具有较强的显著性,特别是在b=-2对应的损失函数下;二是由于这里只考虑了正态误差的情形,预测效果最好的的确是XP*对应的模型,其次是XGK*的模型,两个模型(特别是XP*)的预测效果显著地好于其他几个.尽管采用不同的损失函数得到的平均损失值有些差异,但是考虑了显著性之后,基本可以按照预测能力强弱将上述八种模型做如下的分类:第1类是XP*与XGK*对应的模型;第2类是XP和XRS*的模型;第3类是XGK和XC*的模型;第4类是XRS与XC的模型. 表3 模型预测能力的Diebold - Mariano检验结 为了避免两两比较推断所导致增加第一类错误的问题,下面的表4 给出了依照MSE损失函数(即b=0)采用Hansen[25]给出的Bootstrap方法进行多重比较的部分结果.比如,如果选择C即GARCH模型作为参照,该检验判断它相比其他7种模型是否具有所谓的超预测能力.因为表4中三种设置给出的SPA检验的p-值都很小,因此可以断定在另外的7种模型中至少存在一个预测能力超过GARCH模型.类似地,选择C*、P、GK、RS、RS*等作为参照,都可以拒绝SPA的原假设.相比之下,采用GARCH-P*以及GARCH- GK*作为参照,则无论是在正态误差还是t分布误差的设置下,都无法拒绝这样的假设.因此可以认为,SPA的检验再次印证了前面得到的预测能力次序的结论.波动率代理值取为RRV时结果类似,不再赘述. 为了考察几种模型对上证指数下一个交易日VaR及CVaR的预测能力,本文依照前面的滚动窗口设计拟合模型并得到未来一个交易日的波动率预测值,以拟合窗口内收益率的样本平均值作为均值的预测值,基于估计模型时对条件分布的设定及给出的波动率预测值来得到VaR和CVaR的预测值.表5给出了采用不同模型预测置信水平95%的VaR和CVaR的结果对比. 从对VaR的预测来看,本文提出的七种模型的损失函数值均小于GARCH模型对应的值,而且,后面六种利用了日内最高价和最低价等极值价格信息的模型给出的损失函数值与GARCH模型的结果存在着显著性的差距.结合损失函数以及DM检验的结果,显示出GK*和RS*模型对VaR的预测效果是最好的.另外能够看出,带*的模型比对应的不带*的模型的预测效果要好,这意味着考虑无交易时段并利用开盘价的信息的确可以提高对VaR的预测效果.SPA检验的结果显示后面的四种模型具备对VaR值的超预测能力. 对CVaR的预测结果基本上和VaR的情形是相似的.比如本文七种模型的预测效果都比GARCH的效果好,而且,除了GK和RS之外,与GARCH相比的优势都具有一定程度的显著性.对比带*和对应的不带*的模型,显示出考虑无交易时段的存在对于预测CVaR的作用也是正向的.与VaR的结果不同的是,SPA检验显示出后面六种模型均具备对CVaR的超预测能力.相比文献[34,35]的工作,本文的结果则进一步印证了充分地利用低频价格信息对于风险管理具有实质性的意义. 表4 Hansen的超预测能力(SPA)检验[25] 注:1)该表分别给出了基于两种误差分布设置时依据MSE损失函数给出的SPA检验结果; 2)表中每行代表该模型作为参照模型与其它模型比较,拒绝原假设意味着该模型不具备超预测能力; 3)表中p值依据10 000次Bootstrap抽样结果得到,SPAl, SPAc,SPAu分别对应的三种均值向量的设置方式,具体参见文献[25]. 表5 对VaR以及CVaR预测结果的比 注:1)这里给出的是置信水平95%的VaR和CVaR的预测效果,采用正态条件分布; 2)Loss为预测损失函数加总值; 3)DM给出了与C模型(即常规的GARCH模型)相比的t-统计量值,t-值为正表示该列模型优于GARCH模型,**表示在5%水平下显著,*表示在10%水平下显著; 4)SPA检验给出了Bootstrap的p值,拒绝原假设意味着该模型不具备超预测能力. 本文扩展了传统的GARCH模型的构造思路,将波动率的各种静态估计方法以一种比较统一的形式纳入到了对波动率动态预测的问题当中来,以使得在预测过程中能够使用到了除了收盘价之外的诸如开盘价、最高价、最低价等较为全面的低频价格信息.借助于最近几年发展起来的对波动率高频估计以及预测评价的一些新的进展,本文对上证指数的波动率和风险价值的预测进行了实证分析.结果显示出只要充分地利用收盘价之外的低频价格信息,的确可以显著地改善对波动率和风险价值的预测能力. 众所周知,高频交易信息的获取和处理对于很多人而言还是较为困难的事情,相比之下,如何充分地利用每日的开盘、收盘、最高以及最低等低频的价格信息来获取刻画市场风险及流动性的度量仍然是值得学术探索与实际决策的共同关注,譬如最近Corwin和Schultz[36]利用每天的最高价和最低价对有效价差估计的研究也是基于了同样的关切. 此外,将本文的工作与Hansen和Lunde[18]的研究结果进行对比是有意义的,后者对三百多种ARCH类模型的预测效果进行比较后揭示通过复杂的模型设置并没有显著地提高GARCH模型的预测能力.本文的结果表明了,基于相同的模型设置,通过扩展对其他低频价格的利用,却可以显著地改进GARCH模型的预测效果. [1]Andersen T, Bollerslev T, Diebold F, et al. Modeling and forecasting realized volatility[J]. Econometrica, 2003, 71(2): 579-625. [2]Zhang L, Mykland P A, Ait-Sahalia Y. A tale of two time scales: Determining integrated volatility with noisy high-frequency data[J]. Journal of the American Statistical Association, 2005, 100(472): 1394-141. [3]Parkinson M. The extreme value method for estimating the variance of the rate of return[J]. The Journal of Business, 1980, 53(1): 61-65. [4]Garman M, Klass M. On the estimation of security price volatilities from historical data[J]. The Journal of Business, 1980, 53(1): 67-78. [5]Chou R. Forecasting financial volatilities with extreme values: The conditional auto-regressive range (CARR) model[J]. Journal of Money Credit and Banking, 2005, 37(3): 561-582. [6]李红权, 汪寿阳. 基于价格极差的金融波动率建模: 理论与实证分析[J]. 中国管理科学, 2009, 17(6): 1-8. Li Hongquan, Wang Shouyang. Financial volatility modeling based on price range: Theory and empirical analysis[J]. Chinese Journal of Management Science, 2009, 17(6): 1-8. (in Chinese) [7]孙便霞, 王明进. 基于价格极差的GARCH模型[J]. 数理统计与管理, 2013, 32(2): 259-267. Sun Bianxia, Wang Mingjin. A new class GARCH model based on price range[J]. Journal of Applied Statistics and Management, 2013, 32(2): 259-267.(in Chinese) [8]Fuertes A, Olmo J. Optimally harnessing inter-day and intra-day information for daily value-at-risk prediction[J]. International Journal of Forecasting, 2013, 29(1): 28-42. [9]Rogers L, Satchell S. Estimating variance from high, low and closing prices[J]. The Annals of Applied Probability, 1991, 1(4): 504-512. [10]Patton A. Volatility forecast comparison using imperfect volatility proxies[J]. Journal of Econometric, 2011, 160(2): 246-256. [11]Feller W. The Asymptotic distribution of the range of sums of independent random variables[J]. Annals of Mathematical Statistics, 1951, 22(3): 427-432. [12]Kunimoto N. Improving the Parkinson method of estimating security price volatilities[J]. The Journal of Business, 1992, 65(2): 295-302. [13]Rogers L, Satchell S, Yoon Y. Estimating the volatility of stock prices: A comparison of methods that use high and low prices[J]. Applied Financial Economics, 1994, 4(3): 241-247. [14]Yang D, Zhang Q. Drift-independent volatility estimation based on high, low, open, and close prices[J]. The Journal of Business, 2000, 73(3): 477-491. [15]Buescu C, Taksar M, Kone F. An application of the method of moments to volatility estimation using daily high, low, opening and closing prices[J]. International Journal of Theoretical and Applied Finance, 2013, 16(5): 1-44. [16]Fiszeder P, Perczak G. A new look at variance estimation based on values of minimum, maximum, finish and the drift[J]. Statistica Neerlandica, 2013, 67(4): 456-481. [17]Floros C. Modelling volatility using high, low, open and closing prices: Evidence from four S&P indices[J]. International Research Journal of Finance and Economics, 2009, 28: 198-206. [18]Hansen P, Lunde A. A forecast comparison of volatility models: Does anything beat a GARCH(1,1)?[J]. Journal of Applied Econometrics, 2005, 20(7): 873-889. [19]Hansen P, Huang Z, Shek H. Realized GARCH: A joint model for returns and realized measures of volatility[J]. Journal of Applied Econometrics, 2012, 27(6): 877-906. [20]Glosten L, Jagannathan R, Runkle D. On the relation between the expected value and the volatility of the nominal excess return on stocks[J]. Journal of Finance, 1993, 48(5): 1779-1801. [21]Andersen T, Bollerslev T, Meddahi N. Correcting the errors: Volatility forecast evaluation using high-frequency data and realized volatility[J]. Econometrica, 2005, 73(1): 279-296. [22]Hansen P, Lunde A. Consistent ranking of volatility models[J]. Journal of Econometrics, 2006, 131(1): 97-121. [23]Patton A.Volatility forecast comparison using imperfect volatility proxies[J]. Journal of Econometric, 2011, 160(1): 246-256. [24]Diebold F, Mariano R. Comparing predictive accuracy[J]. Journal of Business and Economic Statistics, 1995, 13(3): 253-263. [25]Hansen P. A test for superior predictive ability[J]. Journal of Business and Economic Statistics, 2005, 23(4): 365-380. [26]Kruse R. Can realized volatility improve the accuracy of value-at-risk forecast?[R]. Working Paper, Hannover: Leibniz University of Hannover, 2006. [27]杨继平, 袁 璐, 张春会. 基于结构转换非参数GARCH模型的VaR估计[J]. 管理科学学报, 2014, 17(2): 69-80. Yang Jiping, Yuan Lu, Zhang Chunhui. Estimation of VaR based on nonparametric GARCH models with Markov regime switching[J]. Journal of Management Sciences in China, 2014, 17(2): 69-80. (in Chinese) [28]Degiannakis S, Floros C, Dent P. Forecasting value-at-risk and expected shortfall using fractionally integrated models of conditional volatility: International evidence[J]. International Review of Financial Analysis, 2013, 27(1): 21-33. [29]叶五一, 缪柏其. 已实现波动与日内价差条件下的CVaR估计[J]. 管理科学学报, 2012, 15(8): 60-71. Ye Wuyi, Miao Biaoqi. Estimating of CVaR with consideration of realized volatility and price range[J]. Journal of Management Science in China, 2012, 15(8): 60-71. (in Chinese) [30]Christensen K, Podolskij M. Realized range-based estimation of integrated variance[J]. Journal of Econometrics, 2007, 141(2): 323-349. [31]Martens M, van Dijk D. Measuring volatility with the realized range[J]. Journal of Econometrics, 2007, 138(1): 181-207. [32]Hansen P, Lunde A. A realized variance for the whole day based on intermittent high-frequency data[J]. Journal of Financial Econometrics, 2005, 3(4): 525-554. [33]Ahoniemi K, Lanne M. Overnight stock returns and realized volatility[J]. International Journal of Forecasting, 2013, 29(4): 592-604. [34]Abad P, Benito S. A detailed comparison of value at risk estimates[J]. Mathematics and Computers in Simulation, 2013, 94: 258-276. [35]张术林. 评估Value-at-Risk模型——条件矩检验方法[J]. 系统工程理论与实践, 2014, 34(5): 1153-1160. Zhang Shulin. Evaluating the Value-at-Risk models: A conditional moment test[J]. Systems Engineering: Theory & Practice, 2014, 34(5): 1153-1160.(in Chinese) [36]Corwin S, Schultz P. A simple way to estimate bid-ask spreads from daily high and low prices[J]. Journal of Finance, 2012, 67(2): 719-760. Volatility forecasting based on daily frequency prices LIUWei-yi1,SUNBian-xia2,WANGMing-jin3* 1. Academy of Financial Risk Research, School of Finance, Capital University of Economics and Business, Beijing 100070, China; 2. Department of Financial Mathematics and Financial Engineering, South University of Science and Technology of China, Shenzhen 518055, China; 3. Guanghua School of Management, Peking University, Beijing 100871, China Within the GARCH-X framework put forward by the authors, this paper considers several new volatility forecasting models based on daily high, low, opening and closing prices of financial assets. These models combine the GARCH modeling procedure and the results of volatility estimation in the early literature, and therefore extend the static estimators into the dynamic driving factors of volatility. Empirical results with the daily prices of the Composite Index of Shanghai stock market over the last decade reveal that the forecasting performances of these new models for volatility and Value-at-Risk are significantly better than the traditional GARCH model. volatility; Value-at-Risk; range; GARCH-X model; forecast 2013-05-12; 2015-05-19. 国家自然科学基金资助项目(71271007). 王明进(1970—), 男, 山东人, 教授, 博士生导师. Email: mjwang@gsm.pku.edu.cn F830; F832; O212 A 1007-9807(2016)01-0060-12
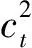
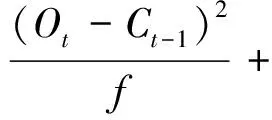
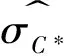

2 GARCH-X模型
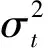
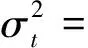
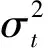
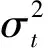
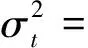
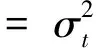
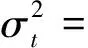
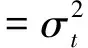
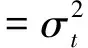






3 模型预测能力的评价
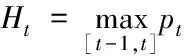
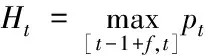
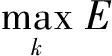
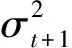

4 实证分析


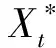




5 结束语

