干涉SAR多基线分析与设计

陈国忠,赵 迪,王晓鹏,侯雨生,陈 亮,张德新

(1.上海卫星工程研究所,上海 201109; 2.上海航天技术研究院,上海 201109;3.电子科技大学 机械电子工程学院,四川 成都 610054; 4.上海交通大学 航空航天学院,上海 200240)

干涉SAR多基线分析与设计

陈国忠1,赵 迪1,王晓鹏2,侯雨生1,陈 亮3,张德新4

(1.上海卫星工程研究所,上海 201109; 2.上海航天技术研究院,上海 201109;3.电子科技大学 机械电子工程学院,四川 成都 610054; 4.上海交通大学 航空航天学院,上海 200240)

为对干涉合成孔径雷达(InSAR)进行优化设计以提高系统的测高精度，对干涉SAR多基线设计进行了分析和研究。用多基线最大似然相位估计方法，比较干涉相位误差最小和相位解缠稳健性最大两种准则，确定选择后者作为多基线系统的基线比例设计准则。给出了多基线长度优化设计方法：先设计多基线系统中的长基线，基于单基线对测高性能的传递模型，按测高精度要求反推长基线的长度范围；再以多基线相位解缠的稳健性最大化为准则进行基线比例寻优，获得短基线长度范围，解决长基线的相位解缠。给出了针对山区地形的一个多基线InSAR系统设计样例，结果表明：采用最大似然法，通过短基线辅助长基线相位解缠，获得了平滑的解缠相位和数字高程模型(DEM)重建结果。该信号处理方法具提高DEM产品精度的潜力。

分布式卫星； 合成孔径雷达； 多基线干涉； 最大似然法； 长短基线干涉； 相位解缠； 相位估计； 基线比例； DEM重建

0 引言

基线是干涉SAR技术中的重要参量，基线长度直接影响图像相干性、测高灵敏度(测高误差的传递系数)，进而影响系统性能。基线越长，测高误差的传递系数越小，但干涉图像对的相干性下降，干涉相位误差也越大，影响高程的测量。基线越短，干涉图像对的相干性增大，干涉相位误差也越小，但测高误差传递系数将越大，也影响高程测量精度。另外，基线的选择还与地形有关，对陡峭区域，基线不能过长。由于上述这些约束条件，使单基线干涉在使用中存在很大局限性。多基线SAR干涉测量有多个基线对应的干涉相位图，可优势互补，在保持相位解缠的稳健性、减小干涉相位误差，提高高程估计精度等方面有其优势，能克服传统单基线SAR干涉测量方法的局限性[1-6]。在系统实现中，传统多基线干涉主要通过单星多航过实现，满足合适的多基线干涉图像对概率较小。随着分布式卫星InSAR系统成为研究热点，以及第一个实际系统TanDEM-X在轨成功运行，对多基线干涉系统优化设计和信号处理的研究有其实用意义[7-9]。

与单基线干涉相同，多基线干涉中各基线的绝对长度对高程估计的精度有很大影响，而且各基线的相对比例对高程估计精度亦有较大影响。对多基线干涉的研究多集中于信号处理，对多基线的优化设计研究较少。文献[10]将多基线等效为雷达阵列间距，从阵列方向图优化角度设计基线长度，实质为三维成像应用。文献[11]从最大后验概率方法出发进行多基线设计，并基于长方体等理想几何体场景仿真进行验证，该法利用了像素间的先验信息。本文基于一种常用的多基线相位估计方法——最大似然法，无需像素间的先验信息，通过比较两种优化准则：干涉相位估计方差的Cramer-Rao界最小准则和多基线相位解缠稳健性最大化准则，优选后者进行多基线设计，并通过长短基线仿真实例进行验证。

1 最大似然法相位估计原理

最大似然法是一种常见的相位估计方法，它利用最大似然准则，从多幅SAR图像中估计解缠后的干涉相位值，可作为基线比例设计的理论依据[1]。

讨论最大似然法相位估计原理。考虑接收星K颗，则有K幅进行干涉的SAR图像，以第1幅图像为基准，其矢量形式可表示为

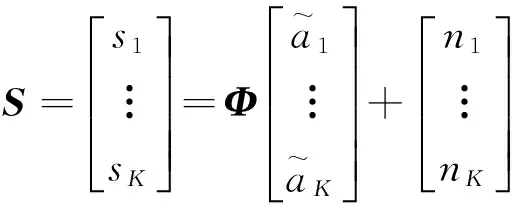
(1)

Φ=

(2)

此处：b1k为第k颗卫星与第1颗卫星形成的干涉有效基线；φ1K为干涉相位；j为虚数单位。式(1)中各相位以第K颗卫星与第1颗卫星形成的干涉相位图φ1K为基准进行表示。

用最大似然法进行多基线相位估计，即可使

(3)

最小的φs(1X)值。此处：L为视数；Cin(m,n)为相干系数矩阵的逆在(m，n)处的值；上标“*”表示共轭。估计的方差用Cramer-Rao界衡量，Cramer-Rao界可表示为

(4)

式中：γmn为相干系数矩阵在(m，n)处的值，即第m，n幅图像对的相干系数；bmn为m，n星间基线相对基准基线(1，K星基线)的比例，且

(5)

至此，得到了用最大似然法进行多基线相位估计的最优值及其对应的基线比例。

以3幅图为例，形成的两根独立基线的比例为0.7，归一化E[f(φ)]随φ的变化关系如图1所示。此处：函数f定义见式(3)。由图1可知：似然函数存在多个相近的极值，导致在噪声较大时相位估计值存在模糊，直接影响相位解缠处理。

图1 多基线系统的似然函数期望值(基线比0.7)Fig.1 Likelihood function of multi-baselinesystem with baseline 0.7

2 多基线系统的基线比例设计准则

根据最大似然法原理，采用多基线相对单基线能提高干涉相位估计精度。多基线的处理性能与多基线配置有关，多基线配置的影响主要表现为相位估计和相位解缠两方面。因此，多基线系统的基线比例设计准则主要如下。

a)准则1：按多基线融合后，干涉相位估计方差的Cramer-Rao界最小为准则进行基线比例寻优。

仍以3幅图为例，取基线比例k为0.5，1.0，相位标准差随相干系数的变化规律如图3所示。图中：SIMO表示一发多收；SISO表示单发单收。由图2可知：双基线时用多干涉相位图的融合可降低相位噪声，进而提高测高精度；基线比例对干涉相位估计精度有影响但并不显著。因此，准则1不适于作为基线比例设计的主要约束。

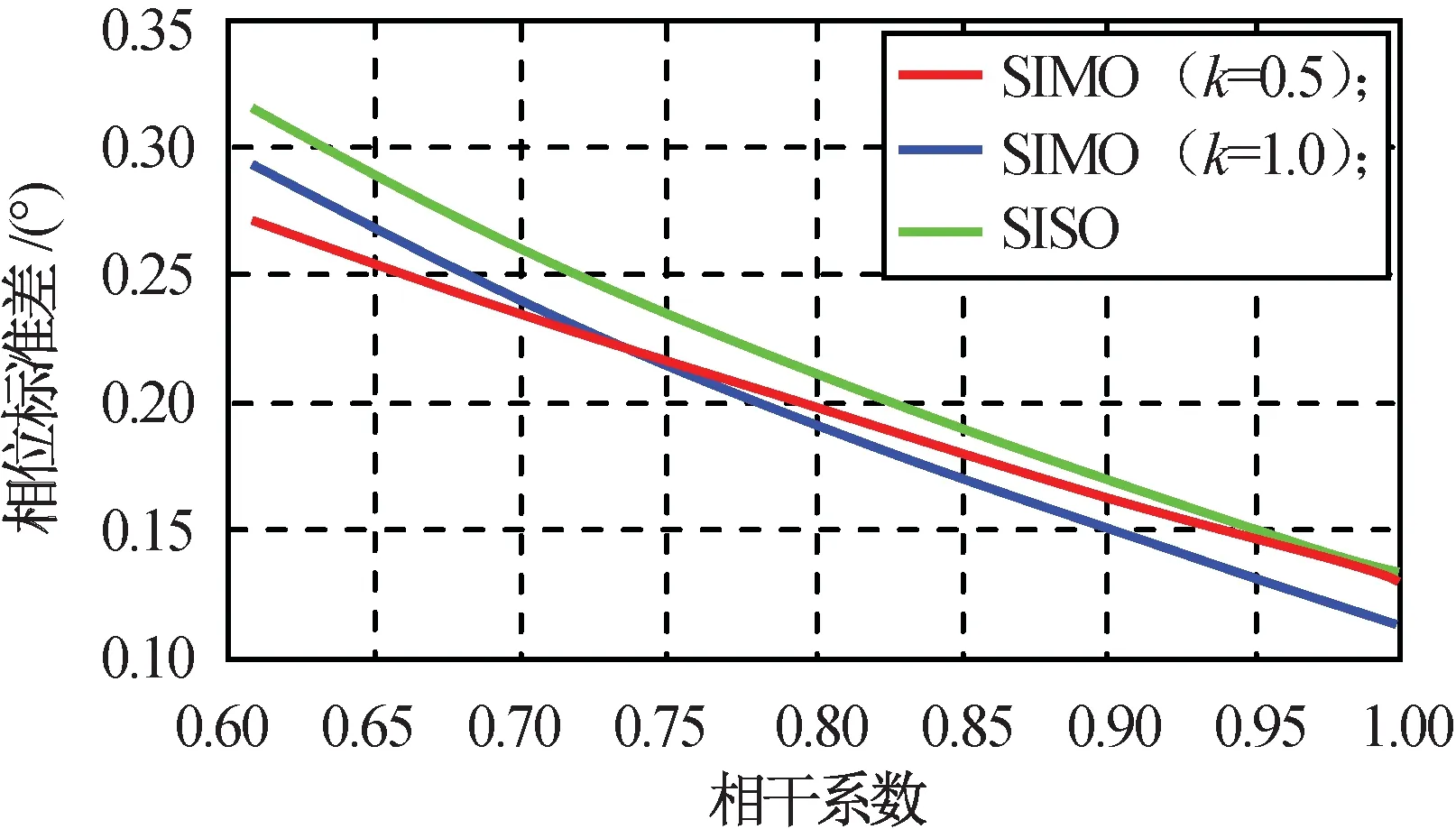
图2 相位标准差随相干系数的变化关系Fig.2 Root phase plot as function of correlation

b)准则2：按多基线相位解缠的稳健性最大化为准则进行基线比例寻优，优化的目标函数是似然函数旁瓣峰值比。

由图1可知：似然函数存在多个相近的极值，相位估计值存在模糊。考虑似然函数与基线比例密切相关，基线比例直接影响似然函数的形状，为此可用似然函数的旁瓣与主瓣比值表示解缠性能，旁瓣相对主瓣的比值越低，解缠性能就越稳健。根据此准则优化基线比例。

因基线较短时，误差传递系数偏大，为满足高精度高程测量需求，必须选择较长基线。但长基线又导致相位解缠难题，这可通过短基线辅助多基线相位解缠处理解决。2010年7月22日，德国TanDEM-X双星系统利用长短基线配合(有效基线长度分别约2 600，200 m)获得了DEM精度达10 cm左右，从原理和实践证明了短基线辅助长基线干涉提高测高精度的可行性[7]。

综上所述，多基线长度优化设计的方法是：

a)先设计多基线系统中的长基线。基于单基线对测高性能的传递模型，按测高精度要求反推长基线的长度范围。

b)再用多基线相位解缠的稳健性最大化为准则进行基线比例寻优，获得短基线长度范围，解决长基线相位解缠难的问题。

3 长短基线分析与设计仿真

3.1 长基线选择

根据单基线与测高精度的约束关系，先进行长基线的设计，得到长基线的长度范围[12]。用仿真分析与设计的方法，确定InSAR性能仿真参数为：卫星高度500 km；信号带宽400 MHz；相位同步剩余误差8°；波束空间重叠率90%；主星定轨精度[2 2 2] m；等效斜距误差4 m；干涉基线测量误差[0.007 0.007 0.007] m；方位向/距离向配准误差0.1像素；沿航迹基线去相干0.95。

考虑长短基线配合主要解决山区的高精度测高，本文针对山地地形(地面坡度25°)进行仿真，给出不同的基线长度及多视处理视数(山地区域分别为9，4视)下，对系统的测高性能进行预估，仿真结果见表1。

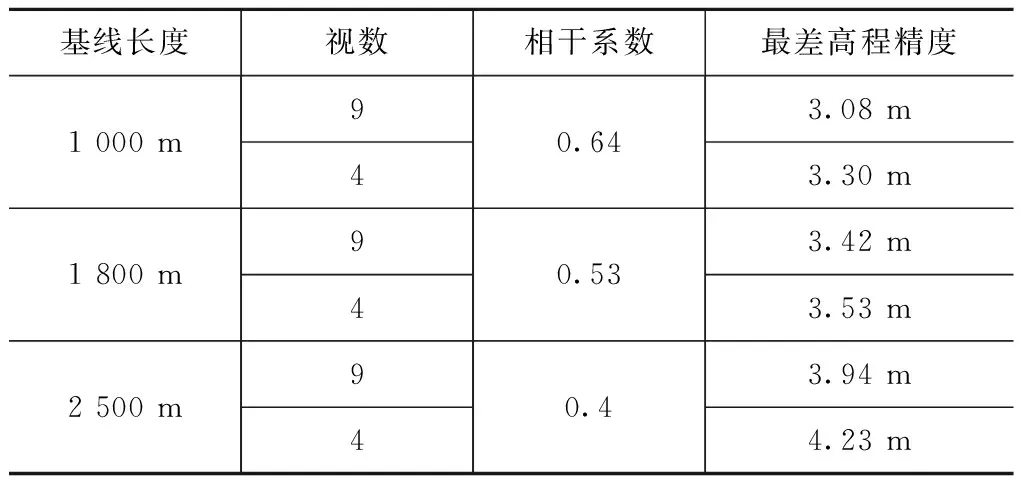
表1 测高性能仿真结果

由表1可得初步结论：从相干性约束来说，当相干系数小于0.5时，干涉相位处理将很难进行。从1∶25 000比例尺测绘标准的要求来说，山地的高程精度优于4 m。依据这两个约束，长基线干涉的基线长度初步范围取为1 000～1 800 m。

3.2 基线比例设计

在长基线分别为1 000，1 800 m时，用似然函数旁瓣峰值比最小准则求解短基线与长基线的比例系数，得到似然函数旁瓣峰值比与基线比例的关系曲线如图3所示。由图3可知：对两种长基线，短基线长度约为长基线的0.1～0.2倍时，多基线解缠的性能最优。按上述多基线解缠性能最优时基线比例的仿真结果，长基线1 800 m时对应的短基线长度应选取180～360 m。

图3 似然函数旁瓣峰值比与基线比例的关系Fig.3 PLSR of likelihood function asfunction of baseline ratio

3.3 仿真实验

基于3星编队针对某山区场景的一组DEM数据进行了信号仿真，基线1长度1 800 m，基线2长度340 m，基线2与基线1的比例约0.19(满足本文的基线设计要求)，得到SAR图像后进行干涉处理，结果如图4所示。

由仿真结果可知：基线1为长基线，其干涉相位对地形起伏更敏感，干涉条纹(图4(a))也更密集，存在条纹断裂，相位残差点多的问题，此时采用单基线相位处理，导致解缠结果出现跳变的现象，DEM重建出现明显偏差(如图4(b)、(c)所示)。基线2为短基线，其干涉条纹图则十分稀疏，能顺利获得相位解缠结果(如图4(d)、(e)所示)，但其DEM重建结果较粗糙，表明测高精度低(如图4(f)所示)。结合长短基线干涉相位图，采用最大似然法，通过短基线辅助长基线相位解缠，获得了平滑的解缠相位和DEM重建结果(如图4(g)、(h)所示)。可见，基于最大似然估计的多基线InSAR信号处理方法具提高DEM产品精度的潜力，仿真验证了用本文基线设计方法得到的短基线能辅助长基线进行相位解缠，进而提高系统的测高精度。

4 结束语

本文对干涉SAR多基线进行了分析并对设计进行了研究。根据最大似然法估计相位的原理，多基线主要从提高相位解缠的稳健性、减小干涉相位误差两个方面发挥作用，因此有两种基线优化的准则：干涉相位估计方差的Cramer-Rao界最小准则和多基线相位解缠稳健性最大化准则。通过比较，本文优选后一准则进行多基线设计，得到多基线长度优化设计的方法为：首先按传统方法得到单基线的长度范围，其次用多基线相位解缠稳健性最大化准则进行基线比例寻优，得到短基线长度范围，解决长基线难以相位解缠的问题。长短基线仿真实例验证结果表明：所设计的短基线能很好地辅助长基线进行相位解缠，验证了本文方法的有效性。本文方法无需像素间的先验信息，适用性强，但后续还需解决基线比例多值性的问题。

图4 仿真数据多基线联合处理结果Fig.4 Results of multi-baseline interfermetric data

[1] LOMBARDINI F. Optimum absolute phase retrieval in a three-element SAR interferometer[J]. Electron Let, 1998, 34: 1522-1524.

[2] ROBERTSON E. Multi-baseline interferometric SAR for iterative height estimation[D]. Provo: Brigham Young University, 1998.

[3] VINOGRADOV M V. Phase unwrapping method for the multifrequency and multibaseline interferometry[C]// Proceedings of IEEE Int Geoscience and Remote Sensing Conference (IGARSS 1998). Washington， DC: IEEE, 1998: 1103-1105.

[4] LI Zhen-fang, BAO Zheng, LI Hai, et al. Image auto-coregistration and InSAR interferogram estimation using joint subspace projection[J]. IEEE Trans on GRS, 2006, 44(2): 288-297.

[5] LACHAISE M, BAMLER R. Minimum cost flow phase unwrapping supported by multibaseline unwrapped gradient[C]// Proceedings of European Conference on Synthetic Aperture Radar (EUSAR 2010). Aachen: IEEE, 2010: 16-19.

[6] HUANG Hai-feng. A fast multi-baseline and multi-frequency band phase-unwrapping algorithm[J]. Measurement, 2014, 49: 401-406.

[8] MOREIRA A, KRIEGER G, HAJNSEK I, et al. TanDEM-L: a highly innovative bistatic SAR mission for global observation of dynamic processes on the earth’s surface[J]. IEEE Geoscience and Remote Sensing Magazine, 2015, 3(2): 8-23.

[9] BORLA TRIDON D B, BACHMANN M, MARTONE M, et al. The future of TanDEM-X: final DEM and beyond[C]// European Conference on Synthetic Aperture Radar (EUSAR 2016). Hamburg: IEEE, 2016: 124-126.

[10] 徐江, 唐劲松, 张春华, 等. 多基线InSAR信号处理中优化阵列的应用[J]. 信号处理, 2002, 18(5): 410-413.

[11] FERRAIUOLO G, MEGLIO F, PASCAZIO V. DEM reconstruction accuracy in multichannel SAR interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(1): 191-201.

[12] 黄海风, 邓泳, 梁甸农. 基于测高精度最优值的星载分布式InSAR编队构形设计方法[J]. 国防科技大学学报, 2005, 27(4): 85-90.

Multi-Baseline Analysis and Design of Interferometric Synthetic Aperture Radar

CHEN Guo-zhong1, ZHAO Di1, WANG Xiao-peng2,HOU Yu-sheng1, CHEN Liang3, ZHANG De-xin4

(1. Shanghai Institute of Satellite Engineering, Shanghai 201109, China; 2. Shanghai Academy of Spaceflight Technology, Shanghai 201109, China; 3. School of Electronic Engineering, University of Electronic Science and Technology, Chengdu 610054, Sichuan, China; 4. School of Aeronautics and Astronautics, Shanghai Jiao Tong University, Shanghai 200240, China)

To optimize the design of interfeometric synthetic aperture radar (InSAR) to improve altimetry data accuracy of the system, multi-baseline InSAR was analyzed and researched in this paper. The two criterions which were the minimum squared-error of interferometric phase and the robust of phase unwrapping were compared by maximum likelihood phase estimation method. The second one was selected as the criterion for designing baseline proportion. The optimal design method for multi-baseline length was given. First, the long baseline was determined. The scope of long baseline length was inversed according to the altimetry requirement based on the transfer model altimetry performance for single baseline. The baseline ratio was optimized by the robust of phase unwrapping criterion for multi baseline. The scope of the short baseline length was obtained to solve the phase unwrapping. The design example of multi baseline InSAR system for mountain terrain was presented. The results showed that the smooth phase unwrapping and digital elevation models (DEM) reconstruction were acquired through long baseline unwrapping assisted by short baseline using maximum likelihood method. The signal processing method proposed has the potential ability to improve the precision of DEM products.

Distributed satellite; Synthetic aperture radar; Multi-baseline interferometry; Maximum likelihood method; Long and short baseline interferomety; Phase unwrapping; Phase estimation; Baseline ratio; DEM reconstructed

1006-1630(2016)06-0026-05

2016-07-20；

2016-08-09

总装备部“十二五”高分辨率对地观测系统重大专项资助(GFZX0XXXXXXX);中国航天科技创新基金资助

陈国忠(1976—)，博士，高级工程师，主要研究方向为卫星总体设计、雷达信号和图像处理。

TN958

A

10.19328/j.cnki.1006-1630.2016.06.003