带大惯量运动部件卫星姿态高精度复合控制研究

刘付成,朱东方,宋 婷,张志伟,黄 静,孙 俊

(1.上海市空间智能控制技术重点实验室,上海 201109; 2.上海航天控制技术研究所,上海 201109)

带大惯量运动部件卫星姿态高精度复合控制研究

刘付成1、2,朱东方1、2,宋 婷1、2,张志伟1、2,黄 静1、2,孙 俊1、2

(1.上海市空间智能控制技术重点实验室,上海 201109; 2.上海航天控制技术研究所,上海 201109)

对有大惯量运动部件的三轴稳定卫星在稳态运行期间高精度高稳定度控制方法进行了研究。提出了一种卫星姿态高精度动态补偿控制算法：先基于卫星姿态动力学模型与卫星有效载荷运动部件摆动规律，设计了姿态稳定反馈控制律和补偿摆动部件干扰力矩的前馈控制器，用前馈-反馈控制的复合控制算法，消除运动部件摆动对卫星姿态控制系统产生干扰力矩的负面影响；再用干扰观测器修正因通信延迟造成的补偿残余力矩，设计了扰动观测器对前馈补偿残余力矩进行辨识，进一步补偿修正残余力矩，以保证控制系统的性能指标。仿真结果表明：该法能有效补偿干扰力矩并提高控制精度，实现的卫星姿态控制精度优于0.005°，姿态稳定度优于5×10-5(°)/s。

卫星姿态； 大惯量运动部件； 高精度控制； 前馈-反馈控制； 干扰观测器； 复合控制； 通信延迟； 残余力矩

0 引言

随着空间任务要求的不断提高，现代卫星的结构越来越复杂，作为卫星的核心部分，有效载荷对卫星姿态高精度、高稳定度提出了越来越高的要求。卫星常携带帆板、天线和多种有效载荷以完成更多的科学任务，各种载荷、天线等在运行过程中需进行摆动，从而产生干扰力矩，影响卫星的姿态控制精度和稳定度[1]。对有扫描相机或凝视相机等摆动部件的空间观测卫星，其载荷或天线体积重量均有较大增加，致使运动部件的惯量亦很大，这增加了高精度控制系统设计的难度。在卫星高精度控制任务中，最基本的挑战之一是有效消除由这些大惯量运动部件引起的周期干扰力矩[2]。在三轴稳定卫星动力学与控制中，卫星转动部件产生的干扰力矩对卫星的姿态运动的影响一般不可忽略[3-4]。特别是转动部件以卫星为支撑平台，卫星姿态同时又会影响转动部件的运动，致使其运动轨迹出现偏差。因此，有必要对卫星姿态所受的由转动部件产生的周期干扰力矩进行分析与估计，并提出相应的补偿方法。对大惯量运动部件的影响，控制系统本身往往不能快速吸收大干扰力矩，这会严重降低卫星姿态的稳定度。为减小摆动部件的运动干扰影响，解决方法一般有两种：一是降低转动部件的角加速度和角速度，但这会影响载荷的性能，甚至不能完成预定任务；另一是用前馈控制器补偿活动部件运动的干扰。对前馈控制已进行了研究。文献[5]研究了预警卫星在扫描相机干扰作用下的姿态稳定控制问题，基于动量守恒定理设计了用于补偿扫描相机干扰作用的前馈控制器，给出预警卫星姿态的反馈-前馈复合控制方法。文献[6]针对三轴稳定卫星在稳态运行期间的姿态精确定向问题，以反作用飞轮为控制系统的执行机构，提出了一种新的基于前馈补偿的高精度卫星姿态控制方法。文献[7]针对平台和附件同时机动时的复合控制进行了初步研究。为尽可能提高前馈的精度，需建立高精度的运动模型和干扰模型，并采用高精度补偿器。虽然利用前馈控制策略复合反馈控制的设计，可实现对无通信延迟干扰力矩的精确补偿，但由于控制系统中信号传输必然存在通信延迟，不确定的通信延迟会造成干扰力矩与补偿力矩的不同步，产生的补偿残余力矩可导致控制系统性能指标下降。因此，还需研究高精度动态补偿控制算法，以实现进一步补偿修正，保证控制系统的性能指标。文献[8]提出了一种基于扰动观测器的鲁棒运动控制方法，现已广泛用于各类电动高精度机械伺服系统。扰动观测器方法将参数摄动、测量误差及各种外部干扰，均折算到控制信号端等效为外部干扰，进而引入相应的补偿，此法可在闭环控制的基础上进一步减小各种干扰和参数变化对系统的影响。扰动观测器方法的计算量少，能满足实时性要求，无需额外的传感器，实现成本低。对扰动观测器在各类高精度伺服系统中的应用研究获得了大量成果[8-11]。如文献[9]综合滑模控制器和干扰观测器，抑制了外部干扰对系统的控制影响，仿真结果表明可获得很高的系统稳态精度；文献[10]针对永磁直线同步电机控制系统，基于干扰观测器的鲁棒反馈控制器补偿了外部扰动、未建模动态、系统参数变化等，保证了系统的强鲁棒性；文献[11]在液压缸系统的高性能位置伺服闭环控制中采用干扰观测器，对各种外部扰动和参数变化进行估计并引入相应补偿，提高了系统运动性能和鲁棒稳定性；文献[12]研究了摩擦对惯性平台跟踪性能的影响，提出用干扰观测器的方法补偿摩擦力矩，仿真结果表明干扰观测器对摩擦干扰力矩有较好的补偿作用，提高了惯性平台的跟踪精度和抗干扰能力。为此，本文先建立航天器动力学模型，分析摆动部件的运动规律，在设计前馈-反馈复合控制律的基础上设计了干扰观测器，实现对残余力矩的辨识以作进一步补偿修正，有效提高三轴稳定卫星姿态控制系统的抗扰性能，并用数学仿真和实时仿真试验对所提方法进行分析和验证。

1 数学模型建立

1.1 三轴稳定卫星姿态动力学模型

考虑以飞轮为执行机构的卫星姿态动力学方程

(1)

(2)

h为飞轮系统在本体坐标系中的角动量；Md为大惯量摆动部件运动产生的干扰力矩和环境干扰力矩等；符号“”表示斜对称阵。

设计控制系统时，为简化过程，设计闭环稳定控制律时忽略干扰力矩，则卫星中心刚体的动力学方程变为

(3)

1.2 运动部件运动规律模型

为实现对卫星装载运动部件摆动干扰力矩的精确补偿，需建立运动部件的摆动规律模型。运动部件的摆动规律一般采用加速-匀速-加速模式或正弦加速度机动模式。本文以正弦加速度机动模式为研究对象，运动规律如图1所示。

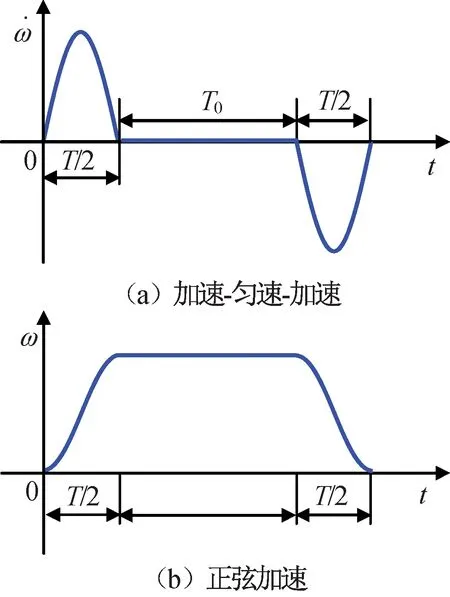
图1 正弦加速度运动部件运动规律Fig.1 Movement character of sine acceleration motion part

根据上述规律，可得正弦型加速度和角速度的机动路径模型分别为

(4)

(5)

式中：T为正弦运动的周期；T0为活动部件保持恒速时间；a为正弦运动的幅值。

2 控制器设计

2.1 前馈控制+反馈控制复合控制策略

因大惯量运动部件在摆动过程中产生的干扰力矩对中心刚体姿态控制精度有不利影响，同时卫星的闭环控制系统无法快速吸收运动部件产生的大干扰力矩，故本文用前馈控制对大干扰力矩进行补偿消除。为尽可能提高前馈控制精度，在建立高精度运动模型和干扰模型的基础上，采用了高精度补偿器，由卫星闭环控制系统和前馈控制构成高精度的复合控制姿控系统，实现对有大惯量运动部件卫星的高精度姿态控制。有大惯量运动部件卫星的复合控制系统原理如图2所示。

图2 复合控制系统原理Fig.2 Principle of compound control system

有大惯量运动部件卫星的复合控制系统包括中心刚体闭环控制回路和干扰力矩补偿的前馈控制回路，其中前馈控制回路主要补偿运动部件的摆动干扰力矩，以提高系统的快速性，改善控制系统性能。当运动部件产生较大的干扰力矩时，需采用专用力矩补偿机构补偿。

2.1.1 闭环反馈控制器

设计有大惯量运动部件卫星的复合控制系统时，先设计卫星的闭环稳定控制回路。采用反馈线性化理论实现卫星三轴间的解耦，得新系统为

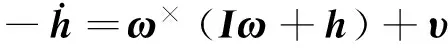
(6)

式中：υ为新的虚拟控制输入[13]。

当卫星的转动惯量矩阵中惯量积非零时，由于卫星本身的特性使卫星的三轴姿态存在耦合。为实现卫星三轴姿态的独立控制，设计卫星的解耦控制器。

为获得三轴完全解耦，设计解耦控制律为

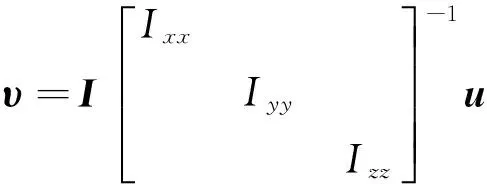
(7)

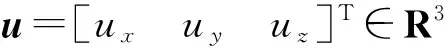
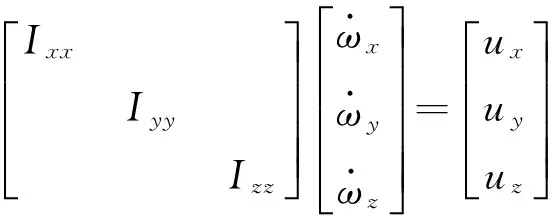
(8)

由式(8)可知：卫星的三轴姿态控制实现了完全解耦。由此，可对每个回路独立进行控制律设计。如对滚动轴控制律，由式(8)可得简化的滚动回路方程为

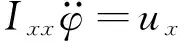
(9)

式中：φ为滚动轴姿态角。

对双积分形式的系统式(9)，可设计工程实现简单并具鲁棒性的PID控制器，有

ux=-kpxφ-kix∫φdt-kdxωx.

(10)

式中：kpx，kix，kdx分别为均大于0的比例增益系数、积分增益系数和微分增益系数。

对转动惯量确定的卫星，可由经典控制理论中控制参数与系统带宽、开环截止频率及相位裕度的关系，根据控制系统的设计目标确定各控制回路的控制参数选择范围，而控制系统的相位裕度可由降低系统截止频率间接获得，以补偿控制回路中延迟时间的影响。得到整定PD控制参数后，在稳态控制回路中可引入积分器以消除系统的稳态误差，以进一步提高系统的控制精度。

2.1.2 前馈补偿控制器

对有大惯量运动部件卫星复合控制系统的前馈补偿回路，实际是采用开环控制方式补偿运动部件的摆动干扰力矩，引入前馈补偿回路并不改变中心刚体闭环稳定反馈控制系统的特性。因运动部件产生的干扰力矩较大，需采用特定的大力矩补偿机构进行补偿。

大力矩补偿机构伺服控制回路采用电流环和速度环双回路设计，其伺服控制系统原理如图3所示。图中：uc为控制力矩；KE电机反电动势系数；Kw为速度环增益；KI为电流环增益；Hs(s)，HI(s)分别为速度和电流控制器；La，Ra，KT分别为电机电枢电感、电枢电阻和力矩系数；Jw为大力矩补偿机构转动惯量；ω为大力矩补偿机构转速；Mf为干扰力矩；Mr为输出力矩。

图3 飞轮输入积分速度控制回路原理Fig.3 Principle of flywheel velocity control circuit

将补偿机构的伺服控制系统传递函数简化为

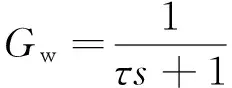
(11)

式中：τ为飞轮伺服系统的等价时间常数。

为实现对大惯量运动部件摆动干扰力矩的精确补偿，需设计大力矩补偿机构的精确前馈补偿控制器。根据大力矩补偿机构的简化模型式(11)，考虑工程可实现性，设计前馈补偿控制器为

(12)

式中：τ≫Tn。

通过采用前馈补偿控制器式(12)，大力矩补偿机构可实现对跟踪指令的精确跟踪。

2.2 基于扰动观测器的复合补偿控制

虽然利用前馈控制策略复合反馈控制的设计，可实现对无通信延迟干扰力矩的精确补偿，但由于控制系统中信号传输必然存在通信延迟，不确定的通信延迟将造成干扰力矩与补偿力矩的不同步，产生的补偿残余力矩可导致控制系统的性能指标下降。为此，设计扰动观测器辨识补偿残余力矩，以实现进一步补偿修正，保证控制系统的性能指标。基于扰动观测器(DOB)的复合补偿控制系统原理如图4所示。

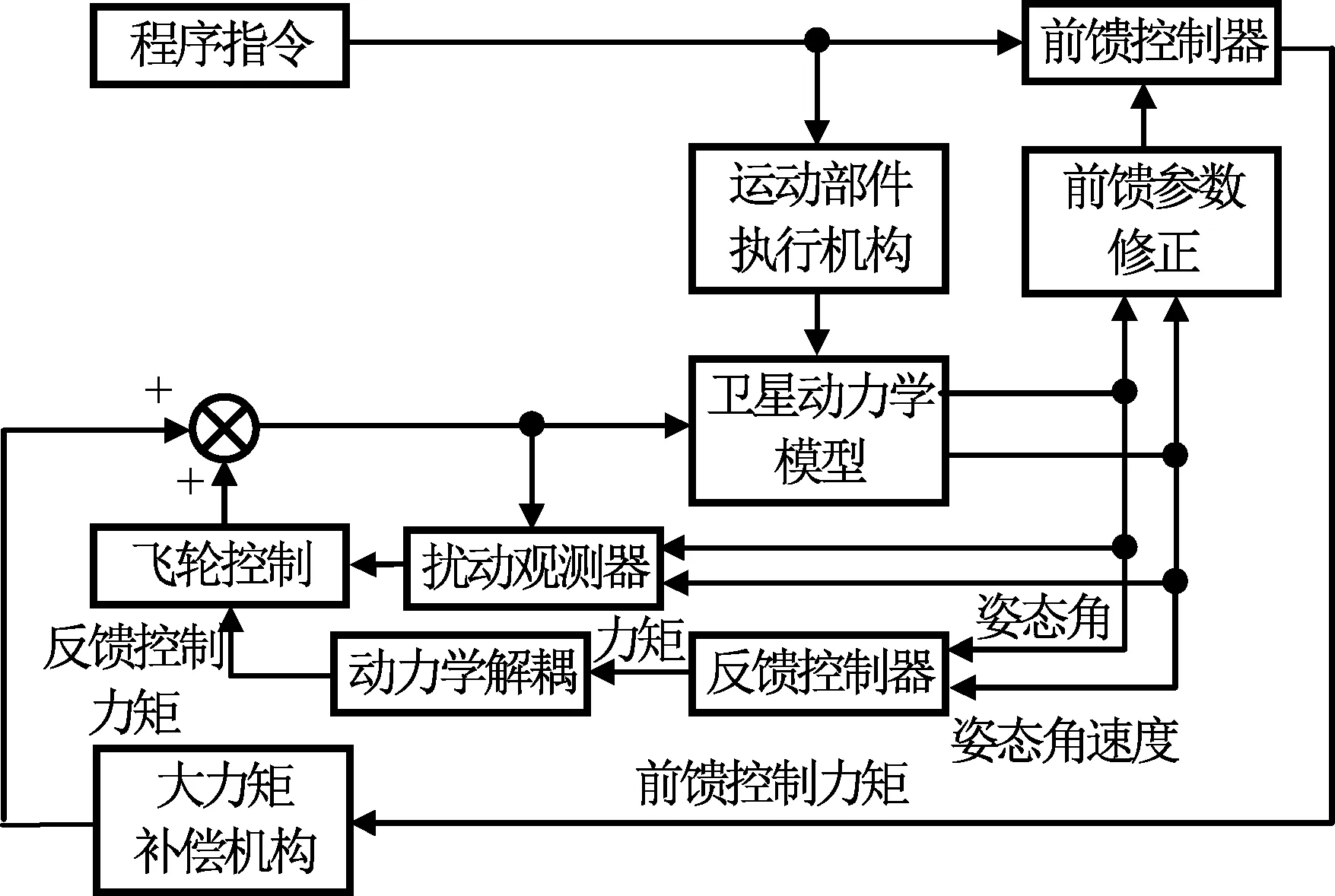
图4 加入扰动观测器的复合补偿控制系统原理Fig.4 Principle of compound control system added DOB

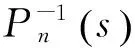
图5 扰动观测器改进结构Fig.5 Modified structure of DOB

假定对象系统为标称模型即P(s)=Pn(s)，且不存在外部干扰和测量噪声(d=0，ξ=0)，则该DOB结构的信号点δ=0，表示DOB结构不是时时参与控制，仅在干扰激励下才发挥控制作用。

设计Q(s)时，使|Q(jω)|，|1-Q(jω)|均尽可能小，同时保证Q(s)分子分母的阶次差程度不低于Pn(s)分子分母的相对阶次。所设计的Q(s)的低频段特性近似为1，实现动态补偿控制器的输出信号，消除包括对象模型摄动及外部干扰等对系统的影响，而Q(s)的高频段特性接近0，实现抑制高频测量噪声目的。

3 数学仿真

为验证所设计复合控制策略的有效性，对某有2个运动部件的卫星进行仿真验证。运动部件A、B的控制方式如图6所示。图中：t0为加速或减速时间；t1为匀速运动时间。

图6 运动部件运动规律Fig.6 Motion law of moving assemblies

设运动部件A的转动惯量6 kg·m2，加速、减速时间0.4 s，匀速旋转速度6.079 8 (°)/s；运动部件B的转动惯量1.9 kg·m2，加速、减速时间0.5 s，匀速旋转速度5 (°)/s；卫星转动惯量

仿真中，执行机构为反作用飞轮，飞轮输出力矩峰值0.2 N·m，带宽10.6 rad/s，最大角动量25 N·m·s。设计卫星的闭环反馈控制器的参数Kpx=Kpy=Kpz=500，Kdx=Kdy=Kdz=1 500，卫星姿态初始偏差为0。在半物理试验平台进行实时仿真，验证本文控制方法的有效性和优越性。

为进行比较，采用同一组控制器参数，分别对未加扰动观测器的前馈+反馈复合控制律和应用扰动观测器的前馈+反馈复合控制律对系统进行仿真。仿真过程中，设定8.6 s时运动部件A开始运动，产生2.5 N·m周期干扰力矩；55 s时，切换至运动部件B工作，产生1.5 N·m周期干扰力矩。

a)无扰动观测器的复合补偿控制

无扰动观测器的卫星姿态角、姿态角速度、输出力矩和补偿残余干扰力矩仿真结果分别如图7～10所示。图中：φ，θ，ψ分别为滚动轴、俯仰轴和偏航轴姿态角。由图7～10可知：由于信号传输过程中存在时间延迟，造成补偿不同步，补偿残余力矩对控制系统的性能产生了不利影响。虽然可实现卫星平台姿态指向精度优于0.005°，但姿态稳定度精度仅1×10-4(°)/s。为进一步提高控制系统的性能指标，须考虑加入扰动观测器。

图7 三轴姿态角Fig.7 Three-axis attitude angular

图8 三轴姿态角速度Fig.8 Three-axis attitude angular velocity

图9 三轴控制力矩Fig.9 Three-axis control torque

图10 补偿残余干扰力矩Fig.10 Compensatory residual torque

b)基于扰动观测的复合补偿控制

加入扰动观测器后的卫星姿态角、姿态角速度、输出力矩和补偿残余干扰力矩仿真结果分别如图11～14所示。由图11～14可知：采用基于扰动观测器的复合补偿控制，可有效削弱补偿残余力矩对控制性能的影响，实现了卫星平台姿态指向精度优于0.005°(3σ)，姿态稳定度优于5×10-5(°)/s(3σ)。

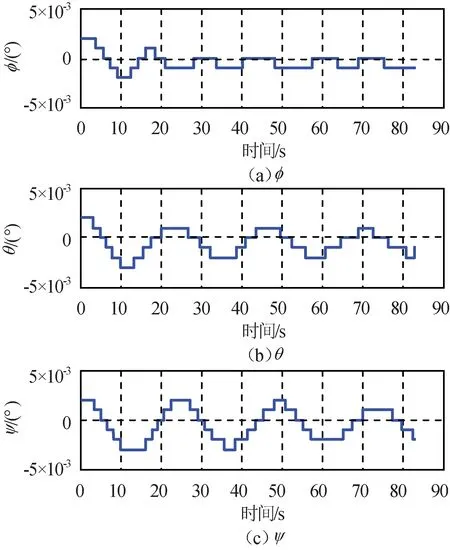
图11 三轴姿态角Fig.11 Three-axis attitude angular

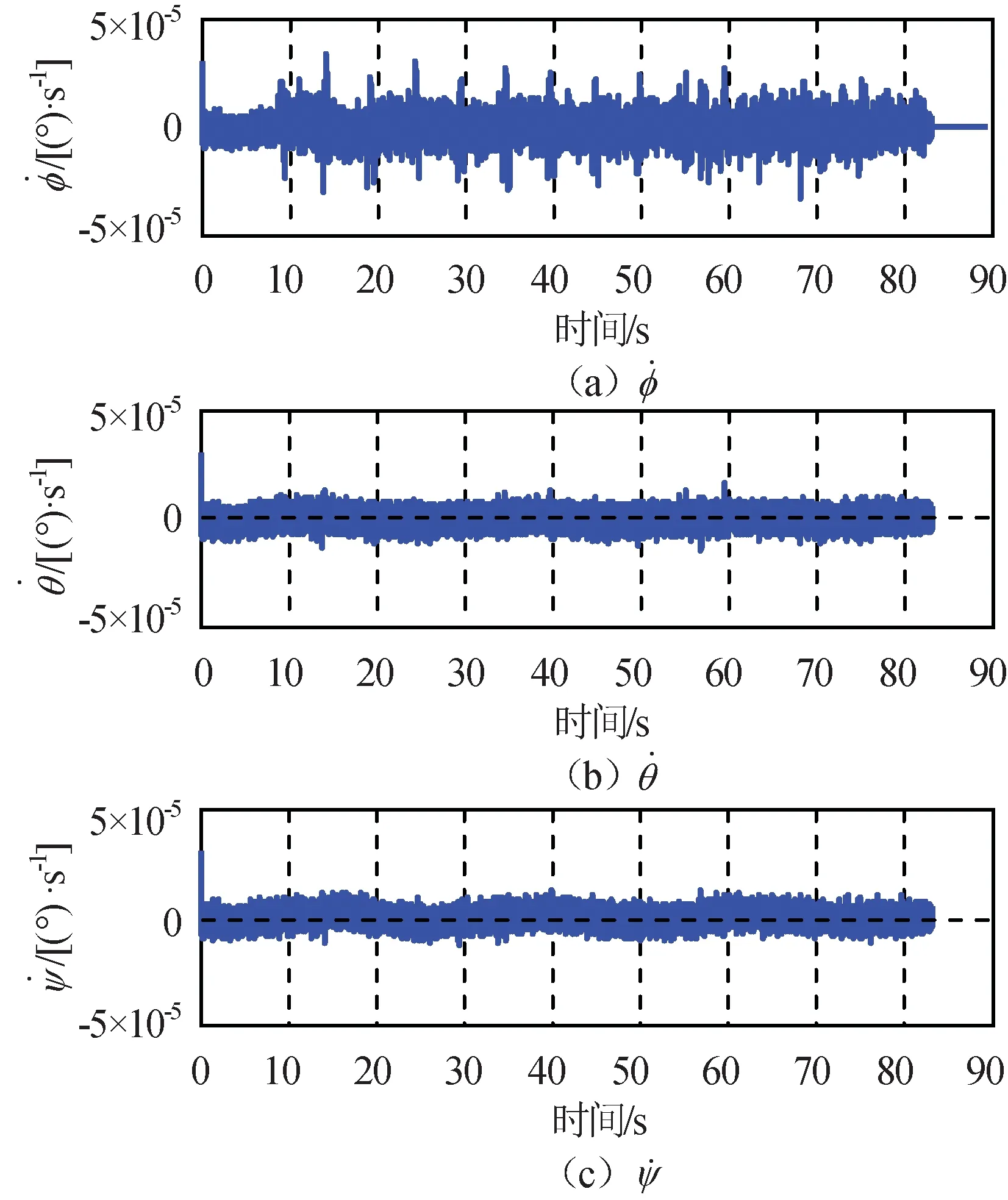
图12 三轴姿态角速度Fig.12 Three-axis attitude angular velocity

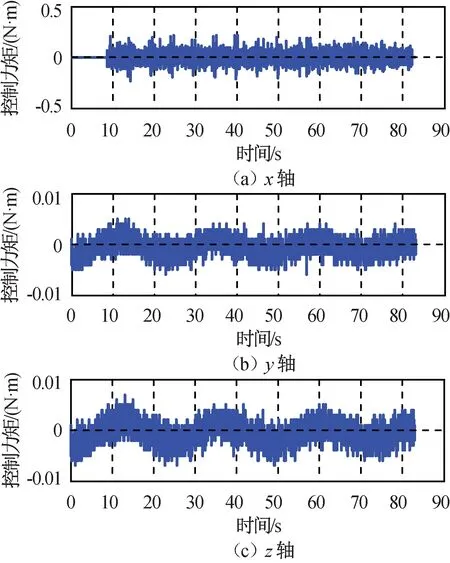
图13 三轴控制力矩Fig.13 Three-axis control torque

图14 补偿残余干扰力矩Fig.14 Compensatory residual torque

4 结束语

本文对有大惯量运动部件的三轴稳定卫星在稳态运行期间高精度高稳定度控制进行了研究。研究结果表明制约航天器控制精度的因素主要有：一是摆动部件的摆动频率，当摆动频率大于控制系统和大力矩补偿机构的响应速度时，必然造成响应延迟，存在残余补偿力矩；二是通信延迟，即使通过硬件同步方式实现摆动部件与大力矩补偿机构运动同步，一般只能达到数十毫秒，无法完全消除通信延迟。针对上述问题，本文先用前馈复合反馈控制抑制卫星上转动部件对系统的干扰，再基于干扰观测器对前馈-反馈复合控制的残余力矩进行辨识，以实现进一步补偿修正，有效提高三轴稳定卫星姿态的控制系统的抗扰性能。半物理实时仿真试验验证了本文提出的复合高精度姿态控制方法的有效性。本文方法通过引入干扰观测器，进一步提高了带大惯量运动部件卫星的控制精度，但干扰观测器的采样频率直接受摆动部件摆动频率的影响，对星载计算机的运算能力提出了较高要求。

[1] HEIBERG C J, BAILEY D, WIE B. Precision spacecraft pointing using single-gimbal control moment gyroscopes with disturbance[J]. Journal of Guidance, Control, and Dynamics, 2000, 23(1): 77-85.

[2] LAU J, JOSHI S S, AGRAWAL B N, et al. Investigation of periodic-disturbance identification and rejection in spacecraft[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(4): 792-798.

[3] MARKLEY F L, BAUER F H, FEMIANO M D. Attitude control system conceptual design for geostationary operational environmental satellite spacecraft series[J]. Journal of Guidance, Control, and Dynamics, 1995, 18(2): 247-255.

[4] 雷静, 刘莹莹, 周凤崎, 等. 卫星在轨周期干扰力矩辨识与补偿方法的研究[J]. 西北工业大学学报, 2009, 27(3): 396-400.

[5] 魏世隆, 曹喜滨, 张世杰. 具有运动部件的预警卫星姿态前馈复合控制[J]. 航天控制, 2004, 22(3): 45-49.

[6] 万九卿, 于劲松, 张伟. 基于前馈补偿的高精度卫星姿态控制[J]. 宇航学报, 2006, 27(6): 1393-1396.

[7] 苟兴宇, 陈义庆, 李铁寿, 等. 平台与附件同时机动及其复合控制初探[J]. 空间控制技术与应用, 2009, 35(5): 1-5.

[8] NAKAO M, OHNISHI K, MIYACHI K. Robust decentralized joint control based on interference estimation[C]∥IEEE International Conference on Robotics and Automation. Raleigh: IEEE, 1987: 326-331.

[9] KIM B K, CHUNG W K, OHBA K. Design and performance tuning of sliding-mode controller for high-speed and high-accuracy positioning systems in disturbance observer framework[J]. IEEE Transactions on Industrial Electronics, 2009, 56(10): 3798-3809.

[10] 赵希梅, 郭庆鼎. 基于ZPETC和DOB的永磁直线同步电机的鲁棒跟踪控制[J]. 中国电机工程学报, 2007, 27(30): 60-63.

[11] 刘强, 冯培恩, 潘双夏. 基于干扰观测器的非对称液压缸鲁棒运动控制[J]. 浙江大学学报, 2006, 40(4): 594-598.

[12] 于爽, 付庄, 闫维新, 等. 基于干扰观测器的惯性平台摩擦补偿方法[J]. 哈尔滨工业大学学报, 2008, 40(11): 1831-1833.

[13] SLOTINE J J E, LI W. Applied nonlinear control[M]. New Jersey: Prentice Hall, 1991.

[14] UMENO T, HORI Y. Robust speed control of dc servomotors using modern two degrees-of-freedom controller design[J]. IEEE Transactions on Industrial Electronics， 1991, 38(5): 363-368.

High Precision Attitude Compound Control for a Satellite with Large Inertial Moving Parts

LIU Fu-cheng1, 2, ZHU Dong-fang1, 2, SONG Ting1, 2, ZHANG Zhi-wei1, 2,HUANG Jing1, 2, SUN Jun1, 2

(1. Shanghai Key Laboratory of Aerospace Intelligent Control Technology, Shanghai 201109, China;2. Shanghai Institute of Spaceflight Control Technology, Shanghai 201109, China)

The high precision and high stability attitude compound control for a three-axis stabilization satellite with large inertial moving parts was investigated in this paper. A high precision attitude control algorithm of satellite was put forward. First, based on the dynamic model of satellite attitude and movement law of moving parts of satellite payload, the attitude stabilization control and a feed-forward controller to compensate the disturbance torque of the moving parts were designed. The negative effects on the satellite attitude control system due to the movement of the moving parts were eliminated by using feedforward-feedback compound control law. Second, the disturbance observer was applied to amend the compensatory residual torque caused by communication delay. The feed-forward compensatory residual torque was identified by the disturbance observer, which was used to amend the residual torque further to guarantee the performance of the control system. The simulation result is showed that the satellite attitude control accuracy is superior to 0.005° and the attitude stabilization is better than 5×10-5(°)/s.

Satellite attitude; Moving parts with large inertia; High precise control; Feed-forward control; Disturbance observer; Compound control; Telecommunication delay; Residual torque

1006-1630(2016)06-0053-08

2016-02-29；

2016-03-31

上海市扬帆计划资助(15YF1405200)

刘付成(1973—)，男，博士，研究员，主要从事航天器控制系统设计和研究。

V448.2

A

10.19328/j.cnki.1006-1630.2016.06.007