中考数学探究题解析及类型分析

□张宇鑫

（浙江外国语学院科学技术学院，浙江杭州 310012）

中考数学探究题解析及类型分析

□张宇鑫

（浙江外国语学院科学技术学院，浙江杭州 310012）

探究题具有很强的综合性，它考查学生基础知识的同时也考查学生灵活运用数学知识与解决问题的能力．探究题种类烦杂，因此教师要对其进行分类，充分了解各类型的特点，并指导学生有针对性地解答，从而提高学生解答探究题的能力.

初中数学；探究题；开放型；新信息型；存在型

初中毕业和高中阶段招生数学考试是数学课程的重要组成部分，直接反映数学课程设计和数学课程内容的新思想、新理念，是反映数学教育质量的一个重要因素.纵观历年各省中考数学试卷，探究问题出现的频率很高，而且探究题知识面的覆盖越来越广，具有很强的综合性，在考查基础知识的同时也检验学生灵活运用数学知识与解决问题的能力．

探究题类型比较烦杂，以问题表现形式来分，大致可归类为开放型、新信息型、存在型等.本文以2015年浙江各地探究题为例，从探究题的类型特征及解析特点出发进行一些探讨，为教师和学生提供一些借鉴．

一、开放型探究题

开放型探究题按题型结构分为条件开放型、结论开放型与策略开放型.此类探究题注重考查学生思维的严谨性和培养发散思维的能力.

例1（2015年绍兴卷）正方形ABCD和正方形AEFG有公共顶点A，将正方形AEFG绕点A按顺时针方向旋转，记旋转角∠DAG=α，其中0°≤α≤180°，连结DF，BF，如图1.

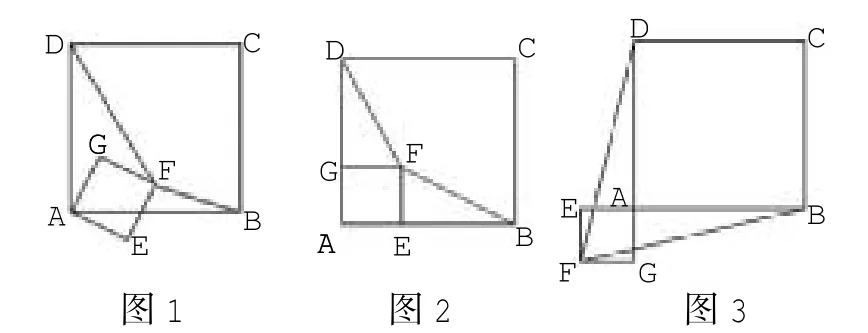
（1）若α=0°，则DF=BF，请加以证明，如图2；

（2）试画一个图形（即反例），说明（1）中命题的逆命题是假命题；

（3）对于（1）中命题的逆命题，如果补充一个条件后能使该逆命题为真命题，请直接写出你认为需要补充的一个条件，不必说明理由.

评析 第（3）小题属于条件开放型探究题，题目中要求补充一个条件，使得（1）中命题的逆命题成立，即若DF=BF，则α=0°.处理此类问题的手段应以逆向思维为宜，正方形AEFG绕点A顺时针旋转的过程中，我们只需关注F点，其在以AF为半径的圆弧上运动.显然存在两种情况，如图2，图3，使DF=BF.那么我们得补充一个条件用来限制图1这种情况.图2和图3的差别在于F点的位置，即可补充F点在正方形ABCD内的条件；若从α角度方面考虑，图3情况下α为180°，即可提出α<180°的条件.

二、新信息型探究题

在新课标改革不断向前推进的形势下，新信息型探究题逐渐成为考查中的亮点，这类题目通常都会出现一些新的概念、规则、运算等，如何理解和运用题中提供的新信息是处理此类问题的关键.2015年嘉兴卷的“等邻边四边形”、宁波卷的“智慧角”、台州卷的“勾股分割点”都属于新信息探究题.

例2（2015年嘉兴卷）类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”.

（1）概念理解

如图4，在四边形ABCD中，添加一个条件，使得四边形ABCD是“等邻边四边形”，请写出你添加的一个条件.

（2）问题探究

图4

图5

①小红猜想：对角线互相平分的“等邻边四边形”是菱形，她的猜想正确吗？请说明理由；

②如图5，小红画了一个 Rt△ABC， 其 中∠ABC=90°，AB=2，BC=1，并将Rt△ABC沿∠B的平分线BB'方向平移得到△A'B'C'，连结AA'，BC'.小红要使平移后的四边形ABC'A'是“等邻边四边形”，应平移多少距离（即线段BB'的长）？

（3）应用拓展

如图6，在“等邻边四边形”ABCD中，AB=AD，∠BAD+∠BCD=90°，AC，BD为对角线，.试探究BC，CD，BD的数量关系.

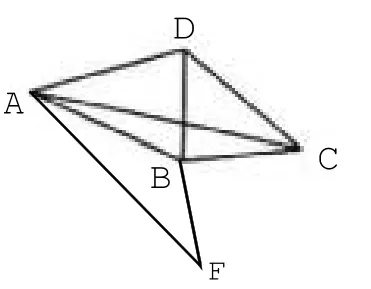
图6

评析 本题属于新定义题型，情景新颖，灵活多变，给学生创设了一个陌生而又熟悉的问题情景.其中第（1）小题为概念理解，绝大多数学生都能够得分.第（2）小题涉及平移问题，抓住平移后对应线段平行且相等的特点，根据定义即可迎刃而解.第（3）小题属于选拔题，涉及相似三角形的判定和性质、多边形内角和定理、勾股定理等内容，同时考查学生的构造思想、分类思想、方程思想.由AB=AD，可将△ABF绕点A旋转到△ABF，构成全等三角形:△ADC≅△ABF，从而得到∠ABF=∠ADC，∠BAF=∠DAC，AF=AC，FB=CD，进而证明△ACF∽△ABD，得到，通过角的转换，证明，根据勾股定理即可得出BC2+CD2=2BD2.其难点在于如何构造三角形BCF，寻找边与边、角与角之间的关系，需要一定的数学素养．

三、存在型探究题

存在性探索问题历来都是考查的重点，几何与代数都有涉及.解决此类问题的一般思路为假设结论成立或存在.结合已知条件，建立数学模型，仔细分析，层层推进，如果能获得相应的结论，则假设成立，如果出现矛盾则说明原假设并不成立.

例3（2015年衢州卷）如图7，在△ABC中，AB=5，AC=9，，动点P从A点出发，沿射线AB方向以每秒5个单位的速度运动，动点Q从C点出发，以相同的速度在线段AC上由C向A运动，当Q点运动到A点时，P，Q两点同时停止运动.以PQ为边作正方形PQEF（P，Q，E，F按逆时针排序），以CQ为边在AC上方作正方形QCGH.

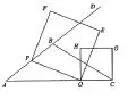
图7

（1）求tanA的值；

（2）设点P运动的时间为t，正方形PQEF的面积为S，请探究S是否存在最小值？若存在，求出这个最小值，若不存在，请说明理由；

（3）当t为何值时，正方形PQEF的某个顶点（Q点除外）落在正方形QCGH的边上，请直接写出t的值．

评析 第（2）问是典型的存在性问题，我们应先假设S存在最小值，在初中阶段，求解最大值和最小值问题比较常用的方法是二次函数最值的运用，首先应想到用PQ的长度来表示正方形PQEF的面积，构造△PNQ，根据勾股定理得出PQ的长度，那么其正方形面积是一个含变量t的二次函数，建立函数模型，注意t的范围，该函数对称轴所在的点即为最小值.

笔者认为，以上分析对探究题教学有以下几点启发.一是要注重对学生思维能力的培养.探究性问题的条件往往不少，关键要引导学生仔细分析，分解问题，归纳解题步骤，只有分析透彻，掌握解题框架，遇见新的问题才能有所思.二是要注重学生良好阅读习惯的养成.在日常的教学活动中，教师应避免唱“独角戏”，要引导学生去阅读课本和相关资料，培养学生自主学习的能力.三是要善于总结归纳.由于探究题基本作为压轴题出现，难度较大，这就需要师生共同总结归纳，此类问题属于哪种探究题，那么对于这种类型的题型，我们首先应想到什么，再想到什么，层层推进，久而久之，学生脑海里会形成一定的逻辑步骤，看到难题不至于毫无思绪.□◢