走出惯性思维的“怪圈”
潘静
(宜兴丁蜀中等专业学校,江苏宜兴 214221)
走出惯性思维的“怪圈”
潘静
(宜兴丁蜀中等专业学校,江苏宜兴 214221)
数学教学中,惯性思维能让学生对同类问题的处理“轻车熟路”、“游刃有余”,积极作用毋庸置疑,教师应该正确引导学生突破惯性思维的负效应,转知为能,促进学生可持续反展。
惯性思维;逆向思维;变式训练
惯性思维是由先前的活动而造成的一种对活动的特殊的心理准备状态,或活动的倾向性,是依据长期积累的思维活动规律和经验教训,在反复实践中形成的定型化的思维方式、轨迹、流程、模式。一般分为两种:一种是积极的,有助于分析和解决新问题,具有正面效应;另一种是消极的,容易阻碍学习者理解和探究新的规律,负面效应明显[1]。
数学学习的核心价值在于问题的解决。解数学问题的一般模式是把有待解决的问题化归为曾经解决过的问题,其过程体现了思维的定向性和连续性。惯性思维不断潜移默化地影响着学生的解题,有时表现为灵活应变,触类旁通,促进问题有效、快捷地解决;有时则会滋生消极作用,使思路闭塞,导向歧途,形成思维惰性[2]。因此,教师应采取“扬正避负”的有效策略,正确引导学生走出惯性思维的“怪圈”。
1 逆向思维觅拓展
逆向思维即反着思考问题,它要求学生从不同的视角、不同的层面、不同的立场去分析思考。逆向思维有两类经典策略。
1.1 喧宾夺主
在一些数学问题中常常含有多个变量,其中有一个变量处于主导地位,称之为主元,其他的变量一般视为参变量即参数,学生在长期反复的解题训练中已经形成一定的解题套路,解此类题型始终抓住主元。但在某些特定的命题条件下,惯性思维却严重制约了思路的拓展,必须另辟蹊径,变更主元。
例1:已知函数f(x)=x2+ax+b,存在实数x0,且有|x0|≥3,使得f(x0)=0,求a2+4b2的最小值。
分析:此题表面来看,是一元二次方程区间根的分布问题。倘若喧宾夺主,以a,2b为主元,把x0看作参数,那么可将方程+ax0+b=0改写为+ax0+(2b)=0,再将a换成x,2b换成y,方程变为x0x+y+=0,此时这个方程可视为关于x,y的二元一次方程,(a,2b)为它的一组解。从几何意义角度理解目标式a2+4b2可以看作动直线(x0在变化)x0x+y+x20=0上一动点(a,2b)到原点的距离的平方,其最小值只需考虑原点到直线的距离的最小值,通过两边平方,令进行换元,拆分后转化为函数依据函数单调性即可求出最小值。
构造出关于(a,2b)的二元一次方程,巧妙地反客为主,是打破惯性思维僵局,拓展解题新思路的关键。
1.2 弃正取反
在数学问题的解答过程中,正面入手比较麻烦或情况过多时,应采用迂回战术,正难则反,大大简化解题的工作量,提高准确率。
例2:A、B、C三位同学参加一家公司的面试,通过的概率分别为,求至少一位通过面试的概率。
解析:此题若从正面入手,必须考虑“A通过B通过C通过,A通过B通过C不通过,A通过B不通过C通过,A不通过B通过C通过,A通过B不通过C不通过,A不通过B不通过C通过,A不通过B通过C不通过”七种情况概率之和,情况偏多,运算复杂,稍有不慎,难免出错。换种思维角度,弃正取反,只需盯住它的对立事件,即三位同学都不通过的概率来求解,显然只有一种情况,简单明了。
2 寻根究底溯本源
数学问题的本源也就是数学教材中隐性的知识以及具有基础性、启发性、衍生性的有价值的知识。教师在教学中往往受制于教学进度和知识容量,忽视了数学知识的来龙去脉,严重影响了学生对问题背后的基本概念的正确认知和理解。
分析:导数是研究函数单调性有力的武器,由于步骤简单,方法明确,深受教师和学生的偏爱。很多教师反复向学生强化解题意识:只要遇到关于函数单调性的问题,一般先求导函数,再根据其正负确定单调区间。若条件给出单调区间,求函数式中参变量的取值范围,那么特别注意增区间对应列式为导函数非负恒成立,减区间对应列式为导函数非正恒成立。学生在反复训练中形成了约定俗成的思维惯性。比如此题,几乎所有的学生都会先求出导函数似乎合情合理,但细心查看会发现,如果把端点值代回原函数化简得是一个常数函数,因此,要去掉a=,从而此题的正确结论是
3 深度变式促提升
在函数奇偶性的教学中,教师不断强化判断函数奇偶性的基本步骤:(1)判断定义域是否关于原点对称;(2)验证f(-x)和f(x)的关系,若f(-x)=-f(x),则f(x)为奇函数;若f(-x)=f(x),则f(x)为偶函数。学生反复练习,对此解题技能已形成了惯性思维,条件反射,即使问题情境变化时,也不能具体问题具体分析,依然对解题步骤张冠李戴。
例4:已知函数f(x)=x2+|| x-a+1,a∈R,判断函数的奇偶性。
分析:学生观察函数解析式的形式为整式型,对自变量x 没有任何限制条件,只需验证f(-x)和f(x)的关系,即可判断奇偶性。
解法:f(x)的定义域为R,关于原点对称。
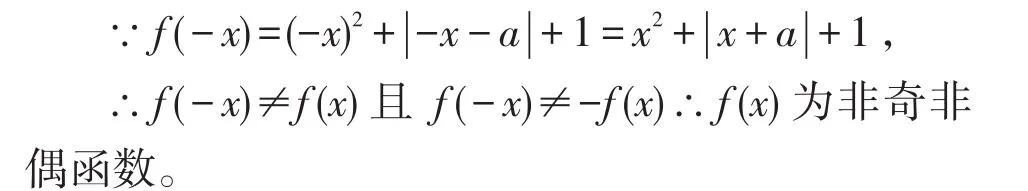
笔者统计后发现,近80%的同学采用这种错误解法。大多数同学都牢记判断奇偶性的步骤,机械化操作,根本没有关注参数a 的影响(需要讨论),没有洞悉奇偶性深层次的含义,不能灵活应对发生变化的问题情境,凸显惯性思维在解题技能上的消极作用。
为了让学生避免惯性思维的认知错误,笔者特意设计一个题组变式训练如下:
(1)若函数f(x)为定义在区间[a,1-2a]上的奇函数,求a的值。
(3)若函数f(x)=aex-e-x为偶函数,求a的值。
8 个小题,从判断奇偶性的各个层面实现多点发散,循序渐进。第(1)题考查函数具备奇偶性的大前提——定义域关于原点对称;第(2)、(3)题考查已知奇偶性求参数的值,提醒学生注意可以用奇偶性定义证明的步骤求解,也可以简化运算用特殊值法求解,但(2)中不能用f(0)=0,避免思维定式的错误,由于定义域中没有零,故只能用f(-1)+f(1)=0来求解,(3)中用f(-1)=f(1),兼顾数学思维的缜密性,得出参数a的值后需要回代检验;第4题意在强调定义域不满足条件,可直接判断为非奇非偶函数,无需验证f(-x)和f(x)=的关系;第(5)题表象带有欺骗性,容易误导,要先根据定义域去掉分母绝对值的干扰,化简后即可明确其为奇函数;第(6)题重点突出既奇又偶函数的形式为f(x)=0,定义域关于原点对称;第(7)题分段函数奇偶性的判断可以根据定义入手,分区间证明;也可以从图像特征直观判断,若图像关于原点对称即为奇函数,若图像关于y轴对称即为偶函数,激发学生化数为形,以形助数的数学思维;第(8)题引导学生关注参数的影响,树立分类讨论的解题思想。
变式训练力求变中有序,变中出新,变中求深,要切合学生的最近反展区,要让学生“跳一跳,摘得到”。学生通过题组的洗礼,很快解决了例4,具体如下:
解析:f(x)的定义域为R,关于原点对称。
当a=0时,f(x)=x2+|| x+1,显然f(-x)=f(x),所以f(x)为偶函数;
解题教学中引入变式训练,可以有效突破惯性思维负面效应,引发学生一题多变、一题多思,从而达到举一反三,触类旁通的理想效果,让枯燥无趣的解题训练变得灵动、智慧。
4 有效反思谋创新
“思接千载,视通万里”,这也是数学教学所追求的理想境界。教师的教与学生的学都提倡反思,学生解题后的反思,不能仅仅停留在对解题过程的常规回顾和简单罗列的肤浅层面,而应深入挖掘、收集解题活动中涉及的思想、方法、经验、规律等。教师要善于引导学生有目的、有方向地反思解题过程中蕴含的思想,涉及的方法,易错的细节,呈现的规律等等。这样学生才能最大程度抵御惯性思维的负面影响,选择的方法更趋于自然、理性,对知识经验的掌握提升到更高的水平。
例5:已知抛物线y2=8x的焦点为F,点A(1,4),点P为抛物线上任意一点,求点P到y轴的距离与||
PA之和的最小值并确定点P位置。例5的解题核心在于距离的转化,要求学生深刻领会抛物线的定义,从知识本源入手,适度转化,源于本质,高于本质。具体实施涉及两次转化,首先将点P到y轴的距离转化为点P到准线的距离减去焦准距的一半,然后再将点P到准线的距离转化为点P到焦点的距离,而A,F位于抛物线的两侧,从几何意义角度考虑,当且仅当A、P、F三点共线时满足条件,故连结AF即可解决。
学生在反思中甄别,在反思中创新,逐渐形成对负面惯性思维的免疫力,合理选择方法,提高探究能力。数学教学是知识的传授,更是智慧的创新,教师要有意识地引导学生形成有效、灵动的惯性思维,在好奇、质疑、探究中拓展新思路,揭示新规律[3]。
[1]范良火.数学算数——英国学校数学教育调查委员会报告[R].北京:人民教育出版社,1994.
[2]张晓贵.数学课堂教学的社会研究[M].合肥:安徽教育出版社,2007.
[3]李士锜.PME:数学教育心理[M].上海:华东师范大学出版社,2005.
(责任编辑 刘红)
Out of the"Circle"of Conventional Thinkingg
PAN Jing
(Dingshu Secondary Specialized School,Yixing Jiangsu 214221,China)
In the teaching of mathematics,conventional thinking can help students on similar problems with"hun⁃dreds of times","easily",a positive role undoubtedly,teachers should guide students to correct the negative effect of breakthrough thinking,thereby to promote students sustainable development.
conventional;reverse thinking;variant training
G718.3
B
1671-0142(2016)06-0025-03
潘静(1984-),女,江苏宜兴人,讲师.

