晷影测年：以陶寺疑似圭尺为例

李 勇

(中国科学院国家天文台,北京 100012)

晷影测年：以陶寺疑似圭尺为例

李 勇

(中国科学院国家天文台,北京 100012)

2002年山西襄汾陶寺城址出土一件残长171.8厘米,且有43个色段端点的漆木杆,疑似标注中天日影的圭尺。为此,文章构建了普适的仅由晷影数据(或刻度)求解圭表观测年代的模型。该模型功能较强,能将未知的表高、圭表间距及太阳位置、观测误差等参数同时解出,可广泛用于圭表测年问题。为求陶寺漆杆的观测年代,设定可允许的最大高度角误差为0.1°,设定表高80～250 cm、圭表间距0～200 cm,步长1 cm；所求年代范围为BC 2201-BC 1901,步长0.001 d。将这些参数和色段端点的数据代入模型处理,并考虑大气折射的影响,结果表明,色段端点中最少有67%与日影无关,故目前判断其为观测日影的圭尺尚存困难。

考古天文学 圭尺 陶寺 中天观测 年代

近年来考古学的发展日新月异,天文考古也有了长足的进步。2003年中国山西省发现世界最古老的天文观象台遗址——陶寺观象台。陶寺遗址、遗物又成了天文史的研究热点。席泽宗院士曾指出：“陶寺天文观测遗迹的发现,是中国考古天文学的真正开端”[1]。

随着天文考古研究的深入,2002年在山西襄汾陶寺城址中期王墓IIM22的头端墓室东南角出土了一件漆杆IIM22:43,残长171.8厘米,受到关注,其功能引起学者们的猜测[2- 6]。它由43个色段端点组成,疑似测量日影的圭尺,这些色段端点用于标识日影。史载周公立表测晷影于阳城,历代重视,数千年不衰,圭表也成为中国古代重要的天文测量工具。李淳风在《隋书天文志》说到立表测晷影可“正位辨方,定时考闰”。针对陶寺漆杆,在没有立表,杆体又残损的情况下,如何利用这些疑似日影的位置获知其可能的观测年代,却成了摆在研究者面前的大难题。

考古学真实地揭示了历史的发展及细节,天文学的发展又实现了某些历史天象的重演。目前,日月行星的运动规律已完全被掌握,在千年尺度上再现其运动历程成为可能。正是在此背景下,人们才开始探索陶寺观象台及漆杆这类疑难的年代问题。为使天文学在考古研究中更为有效地发挥作用,本文试图探索一种普适的仅据圭尺(甚至残存圭尺)上的日影标志(或记录)来求解观测年代等相关参数的方法。其目的在于通过定量研究立表测影问题,建立各观测参数间的内在联系,包括表高、观测年代、这些标志中有多少确系日影等,由此考察晷影观测的细节,进而判断该漆杆测日影用途的可能性。

1 研究方法

目前,多项研究认为陶寺漆杆疑似测日影的圭尺(在古代圭表测日影的系统中,直立的竿称为表,南北水平放置、量度影长的尺称为圭或圭尺),但若想沿此思路定量求解该圭尺的观测细节及年代则极为困难。事实上,在现今的计算机和大数据时代,天文历算早已发展成重要的技术手段用于破解考古天文中的某些疑难杂症,陶寺疑似圭尺问题也不例外。从科学上讲,疑似圭尺问题得以求解的理论依据在于：

(1)早已建立的“误差理论”。晷影观测,或言圭表测影,其天文学内涵为测量太阳中天时的地平高度。该测量系统的误差方程可表示为：

观测值-计算值=min

根据天文历算方法,可获取任意时刻行星际天体的位置,当然也包括太阳每天中天时的地平高度。因本文只涉及单一天体——太阳,及相应的周年周期,处理起来相对方便。具体操作时,本工作就是比对太阳逐日中天时地平高度的“计算值”(由天文历算计算而得)和疑似圭尺上的日影数据,并将其换算成太阳高度数据——即“观测值”间的关系。代入上式即可建立其误差方程,如果它们间的差足够小,就可认定这些观测值或疑似观测值为真——真实的观测值。这就是误差理论的核心,它表明通过日影数据本身即可真实而客观地判断“色段端点是否为日影”的真伪,当然这需要计算出在所考年代区间内每天太阳中天的高度并与观测值逐一比较。换句话说如果已知了这些观测数据就等价于获得本文求解出的一切,包括观测方法、观测年代、观测日期和各种参数,因为这一切都是特定的,显然也是客观存在的。由此可见,针对此类研究对象,可供人们推测的余地其实并不大。

问题在于人们通常只熟悉通过解析式求解一维问题,若解析式中的未知参数过多,经常困扰研究工作的深入,好在“叠代法”的采用恰能处理这类多个未知数的难题。

(2)“叠代法”的应用。“叠代法”其实并不新鲜,它类似以前常说的“待定系数法”。这类参数在计算机程序设计时称之为“循环变量”,它的本质就是在给定范围后,通过规定步长,然后将该范围内的每一值都逐一代入算式计算,进行求解工作,通过比对其与已知值的关系,从而求解出这一“循环变量”的真值。就本文而言我们涉及更为复杂的多重循环计算,变量包括表高H、圭表间距L等。但不管如何复杂,“叠代法”终能保证工作的继续。

(3)计算机大显身手的“穷举法”。例如在研究从A地到达B地的途径问题时,“穷举法”就是将所有可能的道路都通行一遍,最后可根据需要提供出诸如两地最近的道路、需时最少的道路等,问题的答案只有经过“穷举”才能精准得到。早期在面对参数众多的复杂问题时,研究者苦于循环计算的工作量过大,导致人力无法完成。以上“误差理论”和“叠代法”得以实现均离不开计算。当代计算机的应用,可极大提高计算效率,实现“穷举”目的,使众多的未知参数可在求解过程中逐一捕获。试想如果一个研究者不采用计算机,而是通过从SKYMAP等软件中读出观测地每天的太阳中天时刻,再查出中天时相应的太阳地平高度,然后将漆杆上每个色段端点换算成地平高度与其进行比对,加之表高未知、尺端有残等,这一切均要通过叠代和循环处理,逐步进行……如此繁复的工作或许穷尽毕生精力也不易完成。

综上所述,处理陶寺疑似圭尺问题就是此类研究中难度较大的真实案例和样本,本工作的研究表明这类问题将不再是科学的疑难问题和遗留问题。

以上就是本文求解工作的科学本质。

具体的解算方法可描述如下：图1为圭尺中天观测日影的示意图,A、B为漆杆(圭尺)两端,H为表高,L为立表与圭端距离,Xi为端点A距某色段端点的长度。如果陶寺漆杆(或圭尺)上的色段端点确系某年内中天日影的观测记录,则求解其观测时间就是考古实际工作中所遇问题,其难度在于：(1)表高H未知；(2)圭尺从哪端(A或B)计量未知；(3)L长度未知,不能轻易认为L=0,更何况该漆杆A端有残缺,L的设定正是考虑到更为一般的情况。严格说来,对A端而言L=圭表间距+漆杆残损部分的长度,而将漆杆倒置后,对B端而言,L=圭表间距。设定L的优点还在于：用1个值合并考虑2个不确定值,从而减少未知数的个数。如图L+Xi=影长,这样的设定显然也包含L=0的情况,即立表位于圭端的情况；(4)各刻度的观测日期未知。

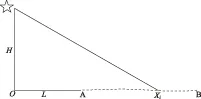
图1 陶寺漆杆中天观测日影示意图(A、B间虚线表示漆杆)

要深入分析和求解圭尺的观测时间,就得借助天文历算方法反演历史时期的逐日太阳中天位置。为此笔者针对已知多组日影标志(数据)专门设计了求解观测时间的模型,包括精确求解出与各数据对应的观测日期,同时还可解出表高H、尺与表的距离L等相关参数。计算采用长周期的DE 406历表,而地球自转长期变化数值ΔT则取自Stephenson等2004年的研究结果[7,8]。

陶寺古观象台遗址位于北纬35.882°,东经111.499°。漆杆上各色段端点的数据见表1,其量度的起点就是漆杆两端A、B。本文对这两种情况分别求解,图1所示系从A点计量日影的情况；若从B端计量,则需将漆杆前后倒置。

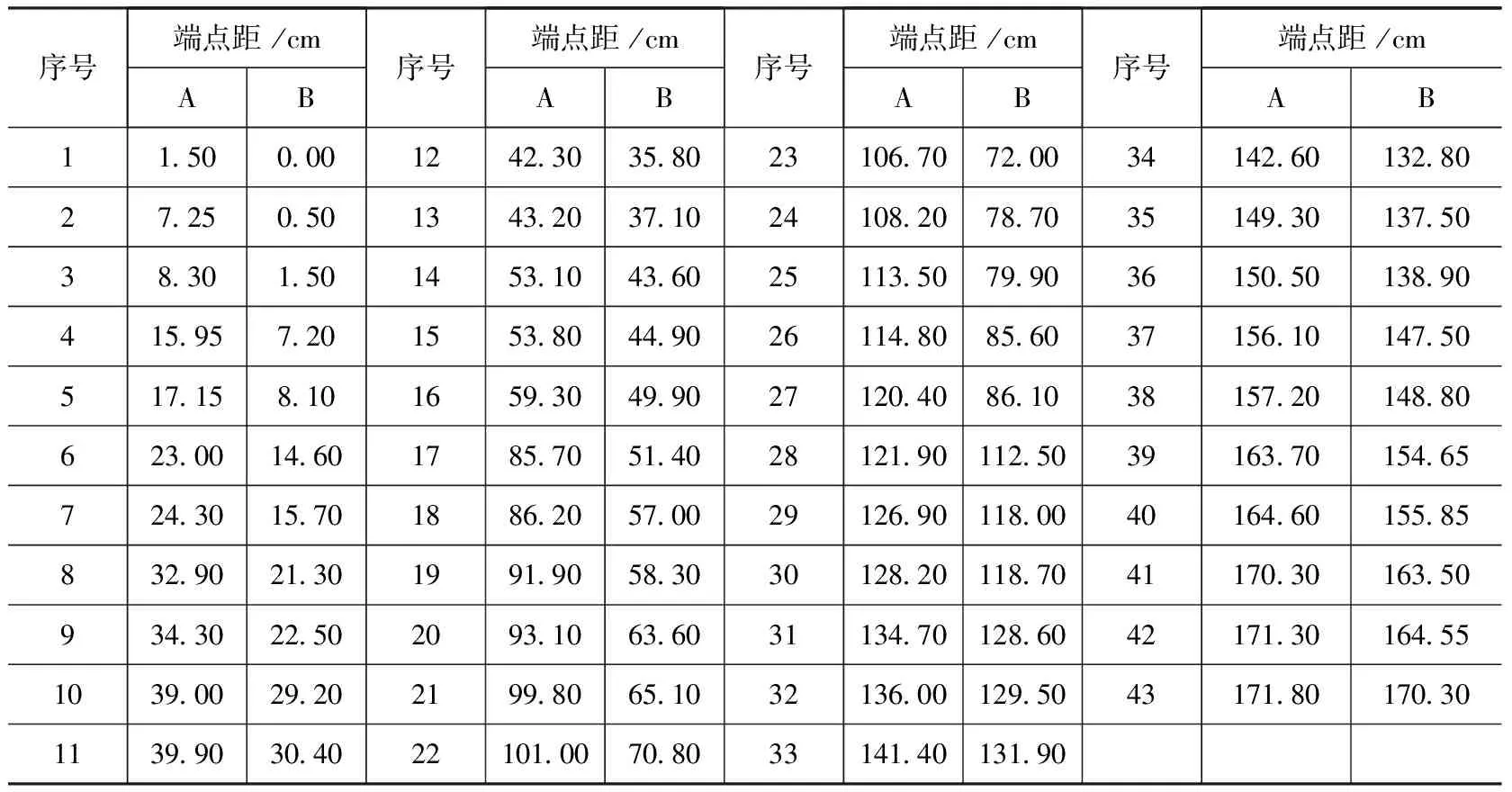
表1 陶寺漆杆各色段端点距漆杆端点A、B的长度Xi值

注： A列数据取自何驽文[6],系从A依次量度A距各色段端点的长度。B列数据则从B点计量,则各端点距=AB间距-A列值=171.80-A列Xi值,但序号须颠倒(因漆杆已倒置),即将序号43值变为序号1值,序号42值变为序号2值,类推到序号1值变为序号43值。这样处理保证影长=L+Xi。例如,倒置后A列的序号1端则到了B列的序号43端点,此时它距B的距离Xi=171.80-1.50=170.30 cm；同理A列序号43端点成了B列序号1端点,其值Xi=171.80-171.80=0.00。

本文只涉及太阳中天时地平视位置的计算,太阳视位置的计算细节可参阅天文书刊,这里只讲述如何利用它来求解圭尺色段上的端点确为日影位置时所对应的最佳观测日期及年代,其具体方案如下：

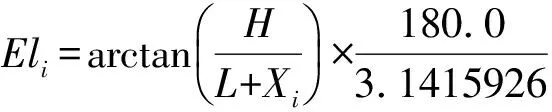
我们设定可允许的最大高度角误差为0.1°,并筛选出Def< 0.1°的结果。计算时需输入的参数有：表高H取80～250 cm,表底距圭端L取0～200 cm,作循环计算时取H和L的增量步长均为1 cm；所求年Year的范围：首年-2200.0,末年-1900.0,计算步长=0.001 d(即1.44 min)；43个色段端点所表示的刻度值Xi；观测中心的地理经纬度；最大角度误差等。将以上数据代入程序并运行即可。本文规定：在误差(Def< 0.1°)范围内,针对每个表高值,(1)以年内符合条件的色段端点(即证实为日影)多者为佳；(2)若色段端点数相等,再以累计的角度误差和Sum小者为佳。由此得到的观测日期序列即为最佳结果。程序设计时考虑了大气折射改正。至于色段的颜色是否具有特殊考古学等含义,本文不做讨论。

2 结 果

具体而言,对于某表高值H,首先,取待定循环参数L和所求年Year,并在BC 2201-BC 1901年内的每一天地方时中午附近,每隔1.44 min计算一次太阳在地平坐标系中的位置,并求解相对于某色段端点Xi的Def值；其次,按上文的规定,当Def<0.1°时,与某Xi相应的结果被记录下来,包括日期、时刻和太阳的高度角(E),随着一次次的叠代计算,取年内Def值最小的那一次为该Xi对于某年的最佳结果,当该年计算完毕后,即得出该年合计可观测到的Xi数(须满足Def<0.1°),以及误差和Sum值；最后,列出具有最多观测Xi和最小Sum值的年份。经过对H循环计算,这样就获得了针对每个H值的最佳观测年(Year),及相应立表与圭尺的距离(L)、可观测到的最大色段端点数(Numbers)、各色段端点与真实日影的误差和(Errors)和表示每个色段端点作为日影的平均误差(Average)。图2(图3)给出了从A(B)端计量漆杆色段端点的针对表高H的最佳结果。

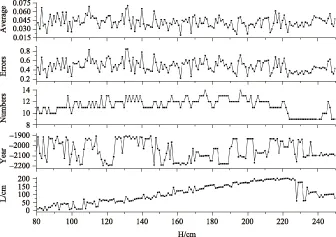
图2 从A端计量漆杆色段端点的最佳求解结果

由于采用复杂的多重叠代求解,需要较长计算时间,本文的设定已有所简化,例如作叠代循环时H和L的步长均取为1 cm,若取0.5 cm,则时间即扩大1倍,同样若时间步长(即1.44 min)再减小,计算的年代区间(BC 2201～BC 1901)再扩大,则计算时间还会更长。即使如此,1台微机仍需工作1500小时以上才能完成。为此,实际操作时可采用多台微机联合求解。

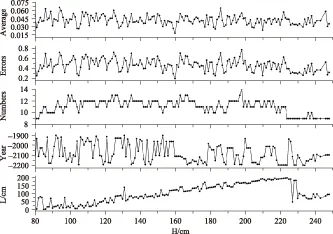
图3 从B端计量漆杆色段端点的最佳求解结果

从图2-3中可见,当H在120～220 cm范围内,L通常随H的增加而加大；观测年份的起伏较大,当H>230 cm时,似从-2200趋向-2100,但此时观测到色段端点数却较少。当H在170～200 cm时(从A端计量),或在200 cm前后(从B端计算)时,可观测到的确系日影的色段端点较多。误差和通常随观测到的色段端点数增加而加大,但无明显趋势。

综合图2- 3,表2给出了10个最佳求解结果。表明：在给定的范围内无论H、L、Year取何值,无论是从A端还是B端计量,这些色段中至多只有14个端点确系晷影。

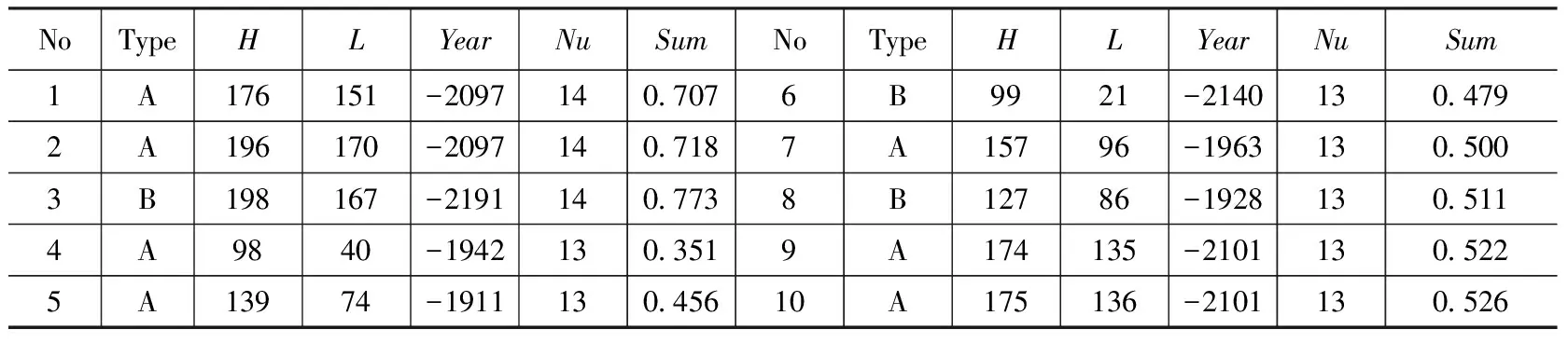
表2 用叠代法求解陶寺漆杆测日影的10个最佳观测年及其他参数1)

1) No为序号,Type指计量端点,H为表高,L为尺端距表的距离,单位cm,Year为年,Nu为符合条件的色段端点数,Sum指累计角度误差,单位为度。

表3列出表2中序号1- 3的详细结果,包括H、L和Year诸值,太阳的地平高度E,相关色段端点序号NXi的观测日期、时间,观测的误差Def及累计色段端点数Nu,包括与0.1°误差相对应的长度值Max和总误差Sum等。

表3 用叠代法求解漆杆测日影的最佳3解1)

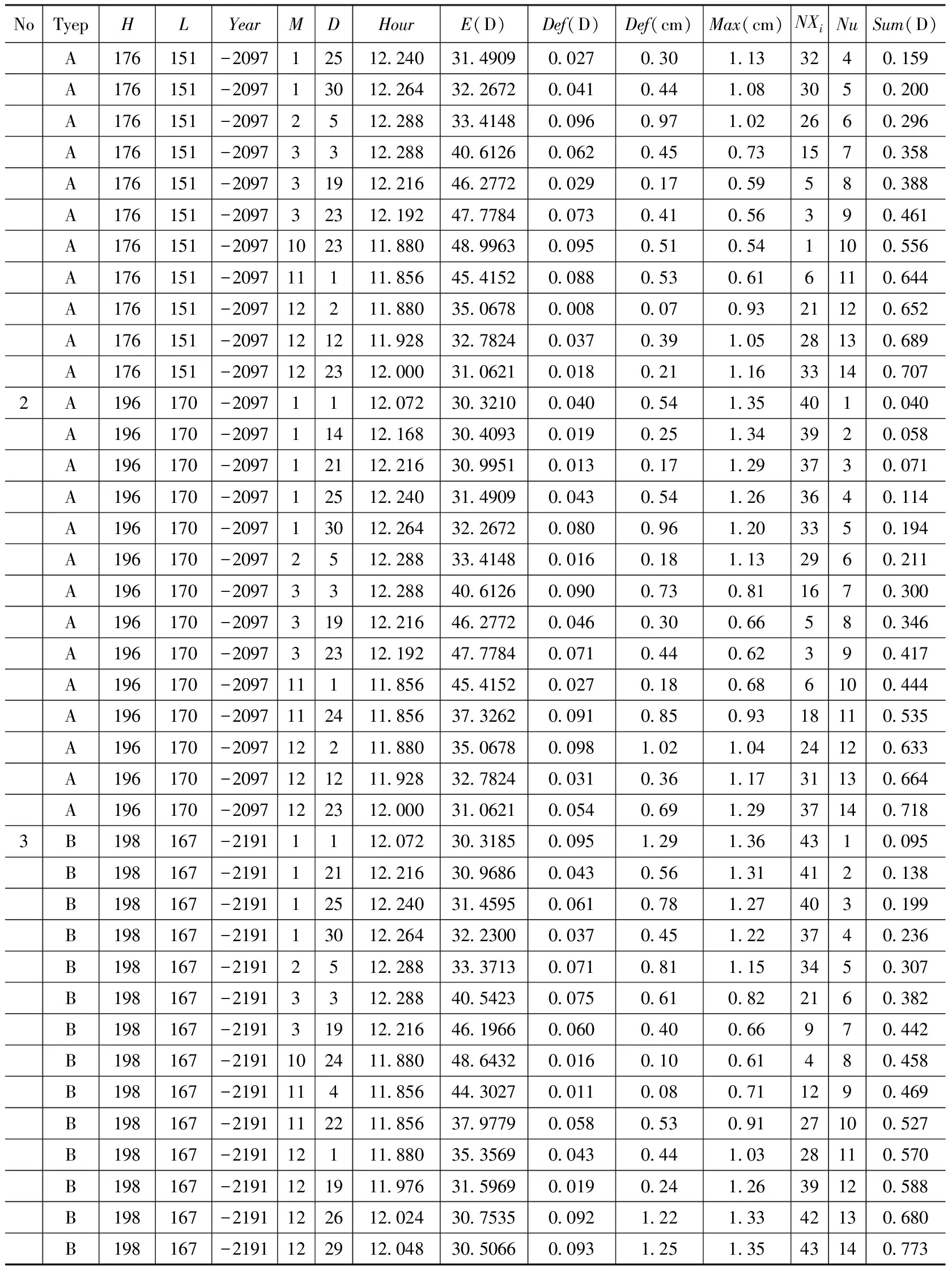
续表3

1) No为序号,Type指计量端点,H为表高,L为尺端距表的距离,单位cm,观测时刻用Year、M、D、Hour表示年、月、日和时刻,E指太阳的地平高度,单位为度,Def为色段端点序号Xi的误差,单位为度和cm,其中Def(cm)=H× [cot(E-Def(D))-cot(E)],将误差换算成长度,Max(cm)为与0.1°误差相应的长度。Nu为符合误差条件(Def<0.1°)的总色段端点数,Sum指累计角度误差,单位为度。

表3所列的3个解中,No 1- 2的年代均为BC 2098,两者都观测到14个色段端点,均从A端计量,但H和L参数不同,前者比后者小约20 cm,且前者的误差和稍小。No 3系从B端计量,H、L参数与No 2相近,观测年份为BC 2192,早于另2个解约100年。

综上所述,在本文所设定的各参数边界条件下,陶寺漆杆最少有67%的色段端点与日影无关,故目前判断它是用于观测日影的圭尺尚存困难。

所谓67%的端点与日影无关,表明在表3所列的最佳年份内任一天的中天日影与这67%的端点(即表3中序号NXi以外端点)其地平高度角相差都大于0.1°。误差小于等于0.1°的端点见表3的NXi列,在各自的最佳观测日(日期和时间亦见表3)其实际高度角误差为Def(D),换算成长度单位则为Def(cm)。同时,表3还给出与最大高度差0.1°所对应的长度为Max(cm),显见Def(cm) ≤Max(cm)。若改变其中的任意参数,则与日影无关的色段端点将多于67%。

所以就陶寺漆杆而言,除非另有充分证据证明该漆杆上确有部分色段端点标注日影,那么本文的求解不仅可确定这些端点的序号(见表3的NXi列),还可得出其相应的最佳观测年代为BC 2098,及其他相关参数(详见表3)。

3 几点讨论

3.1 关于计算方法

立表测影在中国历史悠久,影响深远,逐步演变成古代一项极重要的天文基础测量方法。《元史历志》记元代曾立四丈高表测日影,目的在于推定《授时历》历元——至元十七年(1280年)的冬至时刻[9]。这是作为有史可查的天文历史事件,年代已知,数据保存完整。但作为早期的、考古事件的立竿测影,往往数据不存,年代模糊,甚至立表不在,测量细节不明,就远没有如此幸运。本文构建了由日影中天观测数据求解其最佳观测年代的普适方法,从而揭开了定量研究此类天文考古疑难问题的序幕。对多个未知数问题只有通过叠代方法求解,别无他法。求解时通过天象计算获取太阳中天位置,通过叠代法化解多个未知数问题,通过最小二乘法求出最佳观测时间及相应表高、圭表距、观测日期、太阳位置、观测误差等重要参数。

因H、L、Year等边界条件均不确定,只能经过大量的叠代运算给出完整解的谱系。这是一个功能强大的针对无立表、残存日影数据不完整的圭尺年代计算系统,代价是需占用较多计算时间。而一旦某些边界条件(参数)能确定,则相应解的范围将大大缩小。总之,边界条件越确定,解就越确定。最佳解不全是真解(真解指当时真实的观测时间),真解必为最佳解。因为若这些色段端点真是晷影,它必然满足最佳解的设定,故最佳解可看作是真解的重要参照。

本工作从而深度破解此前难以想象的晷影测年问题。限于篇幅文中只提供了以表高H值(范围80～ 250 cm)为引数的最佳解。当然,要想获得更为精细的结果,可将叠代时间的步长(本文取1.44 min)、H和L的步长(本文取1 cm)减小。此外,Year、H和L的求解区间亦可作调整或放大。这样的参数修改对模型处理十分方便。例如,文中设定表高H的范围为80～ 250 cm,就主要参照了漆杆的长度。

此外,若最佳解中色段端点(晷影数据)的符合率(Nu/N值)较低,即可判断出这些数据(或色段端点)不全是晷影。由此可见,本法亦可用于对太阳中天观测的排除。

3.2 关于测量方式

(1)圭表一体或许不是最佳测量方式

通常圭、表相连,组成一体。《隋书·天文志》称“梁天监中,祖暅造八尺铜表,其下与圭相连。圭上为沟,置水,以取平正。揆测日晷,求其盈缩”[10]。可见最迟在祖氏时期就已造出一体的高精度测日影圭表。但更早期如何,圭表分离似亦很正常。

因观测的细节不明,本文讨论两种情况,即：漆杆上的日影分别从A、B两端计量影长,同时允许表与圭尺间有距离L的存在,这样的处理实际已涵盖圭表一体(即L=0)等众多的情况,更具一般性。实际上据图2、图3,最佳解仅有1次出现在L=0时：系从A端计量,表高H=84 cm,此时观测年份为BC 1912,Nu=11,Sum=0.396。此外,对表2中序号1的最佳解而言,有14个色段端点为日影,且平均每个端点的误差为0.055°。若取L=0,其他参数不变,则得：Nu=5、Sum=0.335,表明只有5个端点与日影有关,且每个端点的平均误差为0.067°,显见这一结果构不成最佳解。当然,还有一种可能就是漆杆上的端点本与日影无关。

(2)参数L的设定覆盖了圭表一体、圭表分离及移杆或翻杆的多种测量方式

考虑到方法的普适性,本文设定参数L取0～ 200 cm,这样的处理兼顾了圭表采用各种位置关系进行观测的情况,首先,L的设定充分保留了各种可能,结果解出L=0,则圭表必为一体；L≠0则必为圭表分离(当然须注意A端有残损,即使L≠0,如果L=A端所残的长度,它仍为一体),此外它还包括可能的移杆或复杆测量。当然,若有充分证据证明圭表一体,模型中亦可直接取L=0,从而简化求解。

例如,百度百科中的“圭表”条就明确有“最早出现的圭表当然都是表杆与土圭彼此分离的简易形制”。何况实际研究时已有学者为保证圭表可测量到冬至日影,提出了移杆测量[2,6]和翻杆测量[4]的设想。为此本文接受这一观点,引入参数L(相当于1根没有读数、长度在0～ 200 cm间可调的杆子),完全实现移杆或翻杆的功能,只是在细节处理上更精准,方便操作。例如,表2中的结果：No.1就解出当表高为176 cm时,漆杆需移杆151 cm,才满足最多的14个端点可观测到,且误差和最小,此时得出的最佳观测年BC 2098。本文的处理只是将这一问题进一步量化。

表3给出的3个最佳解中,均没有冬至日影(其时公历约1月7日左右),有端点的观测日期出现在冬至前后约7日。说明漆杆的端点与冬至不匹配,换言之,若要保证某色段端点的观测日期恰是冬至,则其他可观测到的端点就要减少。或许这也暗示漆杆的端点与日影无关。

(3)到底圭、表是否一体求解即见分晓

尽管通常情况下所见表、圭一体,但也不能排除两者可能的分离。就本问题而言,到底圭、表分离与否,最终还须通过太阳中天观测的历史重建及相应的证据(即表1的数据Xi值)来判定。实际上,研究工作应尽可能多地包含各种可能,而不应“选择性执法”。因陶寺立表全无,研究者无从知晓其体位如何,更不用说是否一体,对此更一般情形,处理时只要增列参数L即可。因为求解结果自会揭晓圭、表到底一体否,这也是本法的神奇处。

L充其量只是一个待定参数,无论圭、表是否一体,最佳解均能反演出该漆杆真实的观测细节,包括如表3所列各相关参数及相应的日期、年代等,而解出的参数L值即可对此做出判断,即通常情况下L=0为圭、表一体,L≠0即为圭、表分离。从本质上讲,观测数据的存在,也就从客观上限定或确定了观测方法,我们的工作就是将其科学地反演出来。正是由于通过端点数据能准确求出参数L值,研究时预设表、圭一体反而不妥,更何况根据考古发掘报告,A处有残,若该漆杆是圭尺,则A并不是真正的圭端。对于从A端计量而言,即使求解结果中L≠0,仍可能圭、表一体,因为此时的L值或许正是漆杆A端所残缺的长度。另外,从数学上讲,一体亦可看作是分离的特例,即两者相距为0。

综上所述,设置参数L并求解之,即完美地解决了圭表是否一体这一问题。

3.3 关于最大高度角误差

设定太阳中天时最大高度角误差为0.1°,其含义是当由天文历表计算所得的当日太阳中天高度角与色段端点所表示的高度角之差不大于0.1°时,就可认为该色段端点为当日真实日影的观测值,0.1°只是允许误差的上限,它通常只与满足条件的结果中精度较差的“日影”有关,而结果中其他“日影”的精度则完全可能远高于0.1°。例如对最优解(表3序号1)而言,色段中有14个端点可认定为日影,误差和为0.707°,平均误差为0.05°,小于设定的0.1°,其中最小误差为0.008°(换算成圭尺上的长度为0.07 cm),最大误差为0.096°(0.97 cm)。

通常天文观测精度都是以角度计量的。对于圭表测影而言,因测量的高度差(角度)与圭尺上的长度呈非线性关系,即同样是0.1°的高度差反映在圭尺的不同位置其表示的长度并不相同。以《周髀算经》为例,立8尺表,冬至影长13.5尺,夏至影长1.6尺,据影长数据可得冬至时太阳的中天高度=arctan(8/13.5)=30.6507°,夏至则为arctan (8/1.6)=78.6901°,若观测误差为0.1°,则冬至时与该误差相应的长度为abs{8尺×[cot (30.6507±0.1)-cot 30.6507]}=0.054尺=0.54寸；同理,夏至为0.15寸。其他节气时0.1°所对应的误差长度则界于这两值之间。可见同样是0.1°的误差,若换算成长度的话,则冬至的误差约为夏至时的3倍多。上述计算中若将表高换成2 m,则0.1°的观测误差,在冬至时相应的圭面长度为1.35 cm、夏至时的长度则为0.36 cm。

另一方面,我们的前期研究表明,元代98次测影的标准误差为4.06’(0.07°),其中最大误差为6.35’(0.11°)[9],鉴于此,再考虑到陶寺遗址的年代早于BC 2000,其观测精度应弱于元代的观测,故本文将其值设定为0.1°。值得一提,陶寺漆杆还存在一个问题,即不少端点的间距过近,最小仅0.5 cm,平均为4 cm。我们所设0.1°时也考虑了实际情况,例如表3所得端点的误差范围Def(cm)为0.07～ 1.29 cm,其中大者即超过了最小的色段长度,故0.1°的设定不能再大了。当然若再减小导致的直接结果是可认定为日影的端点更少。当然若改变0.1°值,对最优解的判定及本文的结论影响不大。

3.4 与观象台关系

通常认定陶寺圭尺比认定陶寺观象台更方便。一方面,漆杆尚存,而观象台顶多只是遗址,地上建筑无存。另一方面,漆杆仅需假设不同色段端点是用以表示太阳中天观测的日影,即使立表不存,一端缺失,仍难不住我们的求解。而另一方面,观象台若成立,则需要一系列假设：(1)该夯土结构的原始建筑曾用于“日出山顶”观测；(2)该建筑的观测缝方位与夯土的柱缝方位相同；(3)四千年来,通过观测缝所观测的东边塔儿山的地形地貌未发生变化,即由观测中心通过观测缝所观测到的山顶地平高度角未变。这些因素都会影响解的不确定性。

当然,以太阳为观测对象的陶寺观象台与陶寺圭尺均可能成立。就观测难度而言,圭尺测晷影较易,此时太阳中天,影南北向,无须考虑方位角,且观测时间在正午附近,易于把握,目的在于建立影长与时节的联系。而通过观象台测日出山顶,难度稍大。观测太阳到此位置的时间,需守候观测,目的可能在于获取祭祀等活动的时间。以上所说也反映出中天测影可能年代更早。我们先期的研究曾得观象台的最佳观测年代当在BC 1956年[11]。本文的研究表明,漆杆最少有67%的端点与日影无关。除非有新证据证明某些色段端点确是中天时的日影标志,若此我们可求出这些色段端点,及其最佳观测年BC 2098,早于观象台约140余年。因圭尺采用的观测设备更为原始简单,而观象台就复杂多了,它不仅结构庞大,建造不易,还需要一个观测中心(观测者的观测位置),故圭尺早于观象台亦好理解。通过独立求解,两者年代似能互洽,相互印证,这难道是巧合？实际上,圭尺求解系统是在观象台的求解系统基础上开发而成,就解算过程而言,前者远比后者复杂,未知参数更多。

1 江晓原, 陈晓中, 伊世同等. 山西襄汾陶寺城址天文观测遗迹功能讨论[J]. 考古, 2006， (11): 81～94.

2 何驽. 山西襄汾陶寺城址中期王级大墓IIM22出土漆杆“圭尺”功能试探[J]. 自然科学史研究, 2009, 28(3): 261～276.

3 Yong Li, Xiao-Chun Sun. Gnomon shadow lengths recorded in the Zhoubi Suanjing: the earliest meridian observations in China？[J].ResearchinAstronomyandAstrophysics, 2009， 9(12): 1377～1386.

4 黎耕, 孙小淳. 陶寺IIM22漆杆与圭表测影[J]. 中国科技史杂志, 2010, 31(4): 363～372.

5 徐凤先, 何驽.“日影千里差一寸”观念起源新解 [J]. 自然科学史研究, 2011, 30(2): 151～169.

6 何驽. 陶寺圭尺补正 [J]. 自然科学史研究, 2011, 30(3): 278～287.

7 Morrison L V, Stephenson F R. Historical values of the Earth’s clock error deltat T and the calculation of eclipses[J].JournalfortheHistoryofAstronomy, 2004, 35(2): 327～336.

8 Morrison L V,Stephenson F R. Addendum: Historical values of the Earth’s clock error[J].JournalfortheHistoryofAstronomy, 2005, 36(3): 339.

9 李勇.《授时历》历元时刻的获取[J]. 天文学报, 2013, 54(6): 569～580.

10 魏征,等. 隋书[M]. 北京: 中华书局， 1973. 524.

11 李勇. 世界最早的天文观象台——陶寺观象台及其可能的观测年代[J]. 自然科学史研究, 2010,29(3): 259～270.

Observing the Year with a Sundial Shadow:The Painted Pole from Taosi as an Example

LI Yong

(NationalAstronomicalObservatories,ChineseAcademyofSciences,Beijing100012,China)

In 2002, the remains of a painted lacquer pole 171.8 cm long marked with 43 colored sections was unearthed at Taosi in Shanxi Province. It has been suggested that it was a ruler used to measure the shadow of the sun when in transit. For this reason this paper designs a universal model to solve the year only from the shadow data of the sun after meridian observation. The model is powerful, as it can be used to derive unknown parameters, such as the height of the pole, the length between the pole and ruler, and observation errors, and also can be widely used in sundial chronology problems. In order to obtain the observing year of this painted pole, we set 0.1 degree as the maximum allowed error of elevation, a height of 80-250 cm for the pole, 0-200 cm for the distance between the pole and the ruler, and steps of 1 cm. We then set the years for between 2201 BC to 1901 BC, its steps 0.001 day, and put all the parameters and data of the 43 colored sections into the model, taking into consideration the influence of atmospheric refraction. Results indicating that at least 67% of the color sections have nothing to do with the shadows of the sun, cast doubt on the theory that the painted pole from Taosi was a ruler used to record the shadows of the sun.

astroarchaeology, ruler to measure the shadows of the sun, Taosi, meridian observation, observing year

2016- 02- 22；

2016- 07- 08 作者简介：李勇，1963年生，四川渠县籍，研究员，研究方向为天文年代学、天文历法、天文考古学、天文地球动力学等。基金项目：国家自然科学基金资助(项目批准号：11403062)

N092∶P1- 092

A

1000- 0224(2016)04- 0383- 12