宽带恒定束宽波束形成的主瓣干扰抑制算法

李 帅，宁立跃，杨小鹏，曾 涛，龙 腾

(北京理工大学 嵌入式实时信息处理技术北京市重点实验室，北京 100081)

宽带恒定束宽波束形成的主瓣干扰抑制算法

李 帅，宁立跃，杨小鹏，曾 涛，龙 腾

(北京理工大学 嵌入式实时信息处理技术北京市重点实验室，北京 100081)

在宽带波束形成技术中，当系统存在主瓣干扰时，通常会导致主瓣畸变、副瓣电平抬高，波束性能严重下降。传统的宽带恒定束宽波束形成算法只能做到主瓣保形，不能有效抑制干扰。因此，提出一种有效抑制主瓣干扰的宽带恒定束宽波束形成算法。该算法构造分频段阻塞矩阵，在数据域实施干扰相消预处理； 补偿预处理带来的信号包络误差，在各频段频率中心采用二阶锥规划方法实现宽带波束的恒定束宽设计。该算法在实现期望信号无失真接收的同时，能有效抑制主瓣干扰。应用计算机仿真验证了该算法的有效性。

宽带波束形成； 主瓣干扰； 恒定束宽； 阻塞矩阵； 二阶锥规划

0 引 言

在数字阵列雷达技术的发展过程中，宽带数字阵列雷达受到越来越广泛的关注。在宽带阵列雷达信号处理中，通常要求宽带信号通过阵列系统后的频谱特性不发生畸变。对于传统宽带波束形成，其主瓣将随着入射信号的频率变化而变化，一般只有当期望信号入射方向与波束指向一致时，才能无失真地接收信号； 当目标在其波束半功率点内其他方向时，输出信号频谱就会失真，对后续信号处理造成不良影响。为了解决这个问题，提出恒定束宽的概念，即主瓣宽度随频率的变化保持恒定[1]。采用宽带恒定束宽波束形成方法，可以很好地解决期望信号来向与波束指向不一致造成的信号频谱畸变问题。

早期的宽带恒定束宽波束形成方法是通过对宽带信号的不同频率分量使用不同孔径的子阵进行接收，由于只能使用有限的子阵，该方法并不能在整个设计信号频带内实现束宽恒定[2]。后来通过把宽带信号划分为若干个子带，随着频率变化改变阵元加权系数来实现波束主瓣宽度恒定。其中，智婉君等[3]针对均匀线阵提出空间重采样方法，利用频率与孔径间的关系，使得各子带主瓣宽度逼近参考频点主瓣宽度； 杨益新等[4]提出应用 Bessel 函数分解设计恒定束宽波束的方法，该方法可用于任意阵列，但是计算量较大； 王大成等[5]提出基于窗函数的恒定束宽波束形成方法； 范展等[6]提出基于凸优化的最小旁瓣恒定束宽时域宽带波束形成方法。

上述传统宽带恒定束宽波束形成方法只能单一满足主瓣宽度恒定，不能有效抑制干扰，尤其是主瓣干扰。基于此问题，提出一种宽带恒定束宽的主瓣干扰抑制算法。

1 信号模型

X(fn)=A(fn)S(fn)+N(fn)

(1)

式中：fn为第n个子带中心频率，n=1, 2, …,J；X(fn) 为M×1维子带接收信号向量;S(fn)为信号在第n个频带的谱分量;N(fn)为噪声在fn处的谱分量；A(fn)=[a(fn,θ0),a(fn,θ1), …,a(fn,θP-1)]为频点fn处的阵列流形矩阵，a(fn,θi)=[1, ej2πfndsinθi/c, …, ej2πfn(M-1)dsinθi/c]T。

2 宽带恒定束宽波束形成的主瓣干扰抑制算法

采用子带设计的方法进行宽带波束形成，使其满足主瓣干扰抑制和恒定束宽两方面的要求。首先将整个宽带信号频带划分为若干子带，在每个子带上构造阻塞矩阵[7-9]，进行干扰相消预处理，接着补偿预处理带来的信号包络误差； 然后选取一个参考频率，得到对应的参考波束图； 最后用二阶锥规划的方法设计得到其他子带上与参考频点具有相同主瓣宽度的波束图[10-15]，从而实现具有主瓣干扰抑制功能的宽带恒定束宽波束形成。

2.1 干扰相消预处理

假设主瓣内存在一个干扰，利用空间谱估计方法对主瓣干扰进行角度估计，得到主瓣干扰的角度信息后，即可对接收数据X进行干扰相消预处理。

设处理后的数据为Y，在第n个子带上有

Y(fn)=B(fn)X(fn)

(2)

式中：B(fn)为(M-1)×M维的预处理阻塞矩阵，且

B(fn)=

(3)

式中：u1=2πfndsinθ1/c，θ1为主瓣干扰的入射角。

设预处理变换前，第k个天线单元的接收信号为

(4)

式中：ui=2πfndsinθi/c。

经式(2)预处理得到变换后的信号为

(5)

Nk(fn)-Nk+1(fn)。

比较式(4)和式(5)，可以看出预处理改变了信号包络，但未改变信号波达方向，并且对于主瓣干扰，其复包络等于0。因此，阻塞矩阵预处理有效抑制了主瓣干扰。

(6)

式中：u0=2πfndsinθ0/c，θ0为期望信号的入射角。

2.2 宽带恒定束宽波束形成方法

为保证恒定束宽波束图不会出现栅瓣，一般选取信号最低频率f1作为参考频率[13]，利用常规波束形成方法得到参考波束图，即

(7)

式中：w1=a(f1,θ0)为参考频点静态权矢量；a(f1,θ)为参考频点在角度θ处的导向矢量。

二阶锥规划是凸优化的一个子集，其标准形式为

maxbTy

s.t.c-ATy∈κ

(8)

式中：y包含有期望变量；A为任意矩阵；b和c为任意向量；κ为一个对称集合；A，b和c的维数必须匹配，且都可以为复数。

为使其他子带波束图主瓣宽度与参考波束图主瓣宽度相同，采用以下优化方法：在保证各子带波束旁瓣低于期望值的条件下，在主瓣内设计各子带波束宽度，使之与参考波束加权均方误差最小，即

(9)

式中：λa(a=1, …, A)为主瓣响应误差加权系数； δb为旁瓣期望值；G1(θ)和Gn(θ)=wHa(fn,θ)分别为参考频率点f1和第n个子带中心频点fn处的方向图；θa∈Θmain(a=1, 2, …,A),Θmain为离散化的主瓣区域，A为其离散点个数；θb∈Θside(b=1, 2, …,B)，Θside为离散化的旁瓣区域，B为其离散点个数。

上述问题可以转化为凸二阶锥规划问题，使用 Sturm 开发的用于处理对称锥优化问题的 MATLAB 工具箱SeDuMi进行求解，最终可得到收敛于全局的最优解。

3 计算机仿真分析

考虑一个接收阵元数为17的均匀线性阵列，阵元各向同性，阵元间距为工作频带上界频率对应的半波长。假设期望信号是线性调频信号，中心频率为f0=1.3 GHz，带宽B=200 MHz，脉冲宽度为T=10 μs，脉冲重复周期为Tr=50 μs，与雷达相距1 500 m，信号波达方向波束指向一致，均为0°，信噪比为0 dB，干扰为宽带噪声压制式干扰，中心频率和带宽与期望信号相同，干扰来向为-3°，干噪比为40 dB。接收机噪声为零均值的复高斯白噪声，功率为1。

对原始输入信号进行脉压，得到的一维距离像如图1所示，可以看出，期望信号完全淹没在强干扰信号中，无法对其进行检测。

图1 原始输入信号的一维距离像

原始输入信号经本文算法处理后，脉压得到的一维距离像如图2所示，可以看出，主瓣干扰得到较好的抑制，期望信号可以被有效检测。

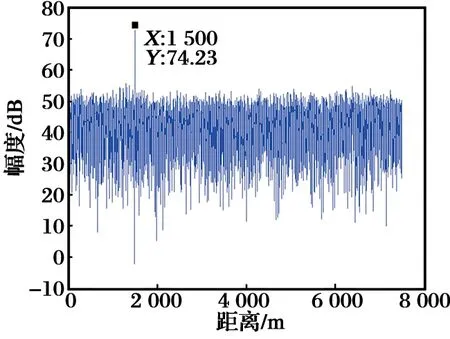
图2 经本文算法处理后信号的一维距离像

频带内不同子带方向图的叠加如图3所示，可以看出，使用二阶锥规划方法能够使不同子带的波束主瓣宽度保持恒定，较好地拟合了参考波束的主瓣形状。另外，在二阶锥规划中对波束图的旁瓣电平进行了约束，因此，恒定束宽波束的旁瓣电平在-30 dB上下波动，具有较好的低副瓣特性。

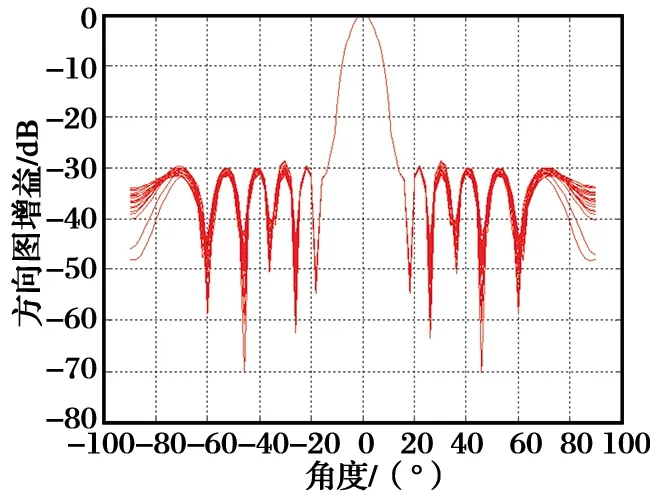
图3 频带内不同子带上的恒定束宽波束图

设雷达接收信号中仅含有期望信号，并使其分别从偏离波束指向2°和6°两个方向入射，经处理后得到的信号分别如图4～5所示。可以看出，采用常规宽带波束形成算法处理后的信号由于在不同频点处增益不一样，时域图出现畸变，且畸变程度随着信号偏离角度的增大而增大。当偏离角度为2°时，信号高频处幅值相对低频处幅值减小10%左右； 当偏离角度为6°时，信号高频处幅值相对低频处幅值减小37%左右。而采用本文算法处理后的信号时域图没有发生畸变，进一步表明本文算法能很好地补偿预处理带来的信号包络损失，同时保证了宽带恒定束宽。

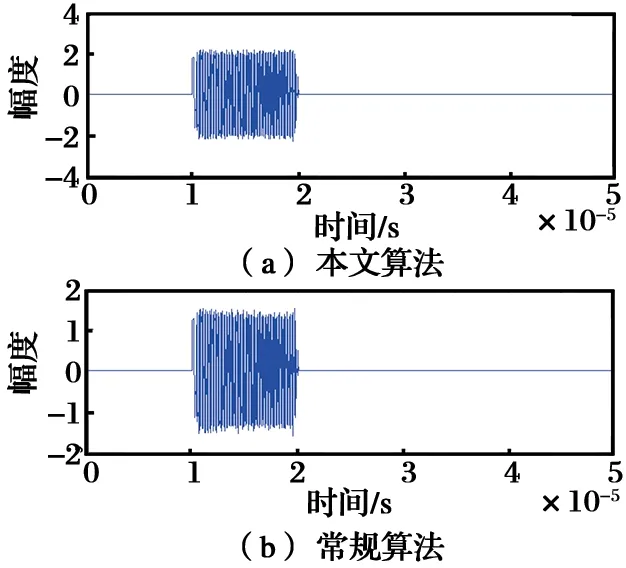
图4 期望信号来向与波束指向相差2°时，不同算法处理后的信号时域图

图5 期望信号来向与波束指向相差6°时，不同算法处理后的信号时域图

4 结 论

针对传统的恒定束宽波束形成算法只能单一满足主瓣宽度恒定而无法抑制干扰这一缺点，提出一种宽带恒定束宽的主瓣干扰抑制算法。通过计算机仿真表明，该算法不仅能保证宽带恒定束宽，而且可以抑制主瓣干扰，从而有效地提高了雷达工作性能。

[1] 唐建生, 孙超. 时域宽带恒定束宽波束形成器的优化设计[J]. 信号处理, 2006, 22(6): 805-809.

[2] 卓光宇. 宽带恒定束宽波束形成算法及其实现[D]. 西安：西安电子科技大学, 2010.

[3] 智婉君, 李志舜. 空间重采样法恒定束宽波束形成器设计[J]. 信号处理, 1998(S1): 1-5.

[4] 杨益新, 孙超. 任意结构阵列宽带恒定束宽波束形成新方法[J]. 声学学报, 2001(1): 55-58.

[5] 王大成, 郭丽华, 丁士圻. 基于窗函数法的恒定束宽波束形成器设计[J]. 海洋技术学报, 2005, 24(1): 113-117.

[6] 范展, 梁国龙. 基于凸优化的最小旁瓣恒定束宽时域宽带波束形成[J]. 电子学报, 2013, 41(5): 943-948.

[7] 高阳, 许稼, 龙腾. 阻塞矩阵抗干扰方法性能分析[J]. 信号处理, 2015, 31(10): 1361-1365.

[8] 罗章凯, 王华力, 张翼鹏, 等. 主瓣抗干扰算法研究[J]. 军事通信技术, 2014，35(1)：16-20.

[9] Yang Xiaoping, Zhang Zongao, Zeng Tao. Mainlobe Interference Suppression Based on Eigen-Projection Processing and Covariance Matrix Reconstruction[J]. IEEE Antennas & Wireless Propagation Letters, 2014, 13: 1369-1372.

[10] Yin Jingxiang. Directional Constant Beamwidth Beamforming by Second Order Cone Programming Constraints[C]∥5th International Conference on Biomedical Engineering and Informatics, IEEE, 2012: 1443-1445.

[11] Chen Peng, Hou Chaohuan, Ma Xiaochuan, et al. Adaptive Broadband Beamformer for Nonuniform Linear Array Based on Second Order Cone Programming[J]. Journal of Systems Engineering and Electronics, 2009, 20(2): 278-282.

[12] Mountcastle P, Henretty T, Naqvi A, et al. Embedded Second-Order Cone Programming with Radar Applications[C]∥High Performance Extreme Computing Conference, IEEE, 2015.

[13] 杨花卫, 黄建国. 一种宽带恒定束宽自适应波束形成算法[J]. 计算机仿真, 2010, 27(10): 339-342.

[14] 刘子龙, 丁淑娟, 孙广俊, 等. 基于二阶锥规划的宽带波束形成器设计[J]. 计算机工程与应用, 2013, 49(5): 195-199.

[15] 幸高翔, 蔡志明. 基于二阶锥约束的方向不变恒定束宽波束形成[J]. 电子与信息学报, 2009, 31(9): 2109-2112.

A Method of Broadband Constant Beamwidth Beamforming with Main Lobe Interference Suppression

Li Shuai, Ning Liyue, Yang Xiaopeng, Zeng Tao, Long Teng

(Beijing Key Laboratory of Embedded Real-Time Information Processing Technology，Beijing Institute of Technology，Beijing 100081，China)

In broadband beamforming technology, the main lobe interference usually causes the distortion of main lobe and the heightening of side lobe level，and the performance of the beam is severely reduced. The conventional broadband constant beamwidth beamforming methods can only satisfy main lobe shapes preserving, but can not effectively suppress the interference. Therefore, a method of broadband constant beamwidth beamforming with main lobe interference suppression is proposed. In the proposed method, the blocking matrices of different frequency bands are constructed and the interference is cancelled in data domain. The signal envelope error caused by pretreatment is compensated and the second-order cone programming (SOCP) is adopted in different frequency bands to achieve constant beamwidth. This method can effectively suppress the main lobe interference while receiving the desired signal without any distortion, and its effectiveness is verified by computer simulations.

broadband beamforming; main lobe interference; constant beamwidth; blocking matrices; SOCP

10.19297/j.cnki.41-1228/tj.2016.06.005

2016-11-03

国家自然科学基金项目(61120106004; 61225005)； 高等学校学科创新引智计划(B14010)

李帅(1991-)，男，山东临沂人，博士研究生，研究方向为自适应阵列信号处理。

TN911.7

A

1673-5048(2016)06-0021-04