基于极值点奇异值降噪与关联维数的电机转子不平衡故障识别

袁 壮，段礼祥，王金江

中国石油大学(北京)机械与储运工程学院，北京 102249

基于极值点奇异值降噪与关联维数的电机转子不平衡故障识别

袁 壮，段礼祥，王金江*

中国石油大学(北京)机械与储运工程学院，北京 102249

提出一种基于极值点奇异值降噪与关联维数分布情况相结合的电机转子不平衡故障识别方法。首先，对不同时期采集的电机振动信号进行基于极值点的奇异值降噪，避免噪声所导致的关联维数不收敛。然后，通过复相关函数法确定延迟时间，并采用G-P算法计算关联维数。最后，对多组振动信号的关联维数进行比较，识别电机转子不平衡故障。利用西部某油田的一起电机转子不平衡故障对上述方法进行了测试，结果表明，降噪信号的关联维数能够有效识别电机转子不平衡，且同常用的自相关法相比，本文采用复相关函数法计算得到的关联维数具有更好的分辨性，更适合于电机故障识别。

电机；转子不平衡；故障特征提取；关联维数

0 引言

电机在工作过程中发生转子不平衡、轴承不对中等故障时，会引起其振动信号的改变[1]。对这些振动信号加以降噪和特征提取，可以进一步了解电机的运行状态及故障类型。但电机运行过程中的振动信号存在大量非线性、非平稳成分，而传统的时域特征和频谱分析都未考虑系统的非线性因素，因而难以客观地描述复杂机械系统的实际状态[2]。

分形几何(fractal geometry)理论用于描述局部与整体在某种形式下的相似性[3]，它体现了自然界中大多数物质的局部与整体在时间、空间、形态和信息等方面的基本属性。分形理论中的关联维数在处理复杂的非线性问题时具有独特的优势，它对系统吸引子的不均匀反应敏感，大小及变化可有效反映信号的不规则度和复杂度，且计算过程相对简单，因而在故障诊断领域得到广泛应用。

王浩、张来斌等提出了将迭代奇异值分解(ISVD)降噪与关联维数分析相结合的烟气轮机故障诊断方法[4]；李琳将关联维数与EMD降噪相结合，对齿轮正常、齿根裂纹、断齿3种不同工况进行了有效识别[5]；王美令提取转静碰摩故障的关联维数和小波能量谱熵为特征量，构造了基于支持向量机的碰摩故障智能诊断模型[6]；杨宇则提出了基于 ITD改进算法和关联维数的转子故障诊断方法[7]。

本文提出了极值点奇异值降噪与关联维数相结合的电机转子不平衡故障识别方法，并运用复相关函数代替传统的自相关函数用于关联维数的求取。对现场实际数据的处理结果表明，该方法更能提升关联维数的分辨性，有利于现场故障的识别。

1 极值点奇异值降噪

实测信号中的噪声会导致关联积分曲线标度区减小，关联维数估计值增大，更会淹没系统确定性特征，因此先要对振动信号进行降噪。本文采用了一种奇异值分解(SVD)降噪的改进方法-极值点奇异值降噪。该方法依据去噪后信号极值点数量随奇异值数目变化的关系，可以准确选取与最优降噪效果对应的奇异值数目[8]。降噪的步骤如下。

1.1 相空间重构

设原始时域信号为X={x|xi(i=1,2,☒,N)}，用时延法重构相空间矩阵：

m为向量个数，n为嵌入维数，m+n-1=N ，设定延时时间为1个采样间隔。

1.2 奇异值分解

对重构矩阵A进行奇异值分解：

U、V分别为XXT的m、n维正交矩阵。S为L维对角阵(l≤min(m,n))，其对角线元素为矩阵A的非零奇异值σi，且σ1≥σ2≥☒≥σl≥0。一般认为，有用信号表现为较大的奇异值，噪声信号表现为较小的奇异值。因此降噪的过程即确定一个阈值σ，将奇异值小于σ的部分置零，得到新矩阵：

式中，S'=diag(σ1,σ2,☒,σ,0,☒,0)，然后对处理过的矩阵进行重构得到降噪后的信号。

1.3 有效秩阶次的确定

由上述介绍可知，降噪效果的好坏取决于'S中不为0的元素个数的多少，即确定合理的降噪阶次K值。目前，对于有效秩阶次的确定，最常用的有试凑法与阈值法，但均依赖于人为经验，缺乏理论依据。因此，本文利用信号的极值点数来确定有效秩阶次。

同有用信号相比，受噪声污染的信号会丧失光滑性，出现大量“毛刺”。当选取的K值较小时，大部分“毛刺”被剔除的同时，有用的冲击等尖锐信号也被滤掉；而随着K的增大，有用信号与噪声被滤除的部分减少，表现为信号中“毛刺”逐渐的增多；当K增大到某一值时，信号有用信息得到最大程度的保留，同时将噪声影响降到最低，这就是要选取的最佳降噪阶次。此时，继续增大K值，噪声的引入将占据主导地位，大量 “毛刺”突然出现，数学意义上表现为大量极值点以远超过之前的速率出现。因此，本文根据降噪后信号极值点数量的变化，找到了其转折突变点，即为应该选取的最佳降噪阶次。

2 关联维数的计算

2.1 G-P算法

G-P算法是一种直接从时间序列中计算关联维数的方法，计算简单，容易实现。

将采集的一维时域信号X={x|xi(i=1,2,☒,N )}用延时法重构得到相空间轨道向量：

式中，τ为延时时间，m为嵌入维数，t=1,2,…,Nm，Nm=N-(m-1)τ。

定义其相关函数为：

其中

Xi-Xj则为任意两个向量间的欧式距离，r为超球半径。

相关函数反映了重构相空间中距离小于r的点对的比例，r若取值过大，则所有点对之间的距离均小于r，所有矢量发生关联，相关函数c(r)=1；取值过小，则所有点对之间的距离均大于r，所有矢量均不相关，相关函数c(r)=0，两种情况都不能客观反映系统的内在性质。因此，适当选取r的范围使得在某个区间内存在

式中，d(m)即为嵌入维数为m时的关联维数。在其具体求解过程中，要先选择关联积分曲线ln(C(r))-lnr的无标度区，并对无标度区内的曲线做最小二乘拟合得到直线，其斜率即为关联维数d(m)。因此，关联维数d(m)的大小主要与延时时间τ、嵌入维数m及无标度区的选择密切相关。

2.2 确定延迟时间τ

延迟时间τ选取的不恰当会严重影响相空间重构的质量，进而影响关联维数。对于延迟时间的确定，较为成熟的是自相关函数法。但这种方法最大的缺点是只考虑了线性关系，而对于具有非线性特征的信号适用性就有所下降。因此，本文选取复相关函数法[9]来确定延迟时间。定义m维复相关函数为：

2.3 确定嵌入维数m

嵌入维数过大，在增加计算量的同时还会放大序列中噪声的影响；嵌入维数过小，则重构的相空间无法反映原系统的动力学特性。本文选择Cao方法[10]来确定嵌入维数。

假定待处理的时间序列为A={ai,i=1,2,…N}，通过时间延迟重构得到向量

其中，m为嵌入维数，τ为嵌入延迟。

定义关于嵌入维数m和延迟时间τ的函数：

Cao方法在假定通过其它方法已经获得最佳时间延迟τ的基础上考虑E(m)随嵌入维数m的变化，因此定义：

随着嵌入维数m的增加，F(m)不断增大，当大于某个值时，F(m)不再发生明显的变化且接近于1时，则此时的维数m即为要找的最小嵌入维数。

2.4 确定无标度区

确定延迟时间以及嵌入维数后，就可根据3.1介绍的G-P算法计算相关函数，画出关联积分曲线ln(C(r))-lnr，并选择无标度区进行最小二乘拟合。但对于无标度区的选择，目前的做法都是观察关联积分函数的曲线，截取双对数曲线中比较接近直线的一段作为无标度区。但这种方法往往存在较大误差，为解决上述问题，本文对关联积分曲线进行滑动五点线性回归，得到局部标度指数曲线[11]，该曲线中的线性区域即为无标度区。

将无标度区内的曲线最小二乘拟合成直线，其斜率即为信号的关联维数值。

3 工程应用及分析

2011年11月西部某油田作业区丙烷压缩机电机发生了故障，经拆机检修发现是轴弯曲引起的转子不平衡故障。选取该电机2010-2012年期间10次采集的振动信号数据，采用上述方法进行关联维数计算。

3.1 原始信号关联维数的计算

选取11月份电机发生故障时采集的振动信号数据，不经过降噪处理，直接对原始信号(如图1所示)进行关联维数的计算。

(1)求解延迟时间τ。利用复相关函数法求延迟时间，得到复相关函数曲线如图2所示。选取曲线第一次下降到零点附近时的时间作为延迟时间。这里取τ= 13 s。

(2)确定嵌入维数n。确定延迟时间后，根据公式9-11，利用Cao方法判断最佳嵌入维数，得到图3。

由图3可以看出，当嵌入维数m增大到22时，函数F(m)增大到1且不再发生明显变化，因此取信号的最佳嵌入维数为22。

(3)选定无标度区。取嵌入维数m的变化范围为10～30，绘制关联积分函数ln(C(r))-lnr曲线如图4所示。从图中可以看出，m变化时，曲线在lnr= 2～2.5范围内趋于平行，表明关联维数不再随m的增大而发生明显变化。

图5为局部标度曲线， lnr= 2～2.5为该曲线的线性区域，进一步说明选择该区域为无标度区是恰当的，此时的曲线斜率即为所求的关联维数。

(4)求解关联维数。对无标度区内的曲线进行最小二乘线性拟合，得到其关联维数d = 1.794 8。

同样，对其他时间段监测的振动信号进行如上处理，依次求取其关联维数，结果如图6所示。

分析如上结果可知，各时期所测振动信号的关联维数值不具有分辨性，2011年11月发生故障时的关联维数同其他时间的正常状态相比并无明显差别。这主要是由于关联维数对噪声比较敏感，而现场信号噪声过大，致使系统内在的确定性特征被淹没，关联维数无法反映系统真实状态。因此，求解关联维数之前，必须对信号进行降噪处理。

图1 振动信号时域波形图Fig. 1 Time domain vibration signal waveforms

图2 信号复相关系数图Fig. 2 Complex auto-correlation coeffcient sketch of the signal

图3 信号的局部标度指数图Fig. 3 Local scaling exponent sketch of the signal

3.2 降噪信号关联维数的计算

同样采用3.1中的振动信号，利用1中提出的极值点奇异值降噪法对其进行处理。降噪前后的时域波形图如图7所示。

从图7可以看出，降噪后信号中的噪声含量明显减少，信号的标准差也由4.04下降到了3.94，证明极值点奇异值降噪法成功起到了抑制噪声的作用。继续采用3.1中的步骤对降噪后的振动信号求取其关联维数d = 2.277 3，同时，各时期所测信号降噪后的关联维数值如图8所示。

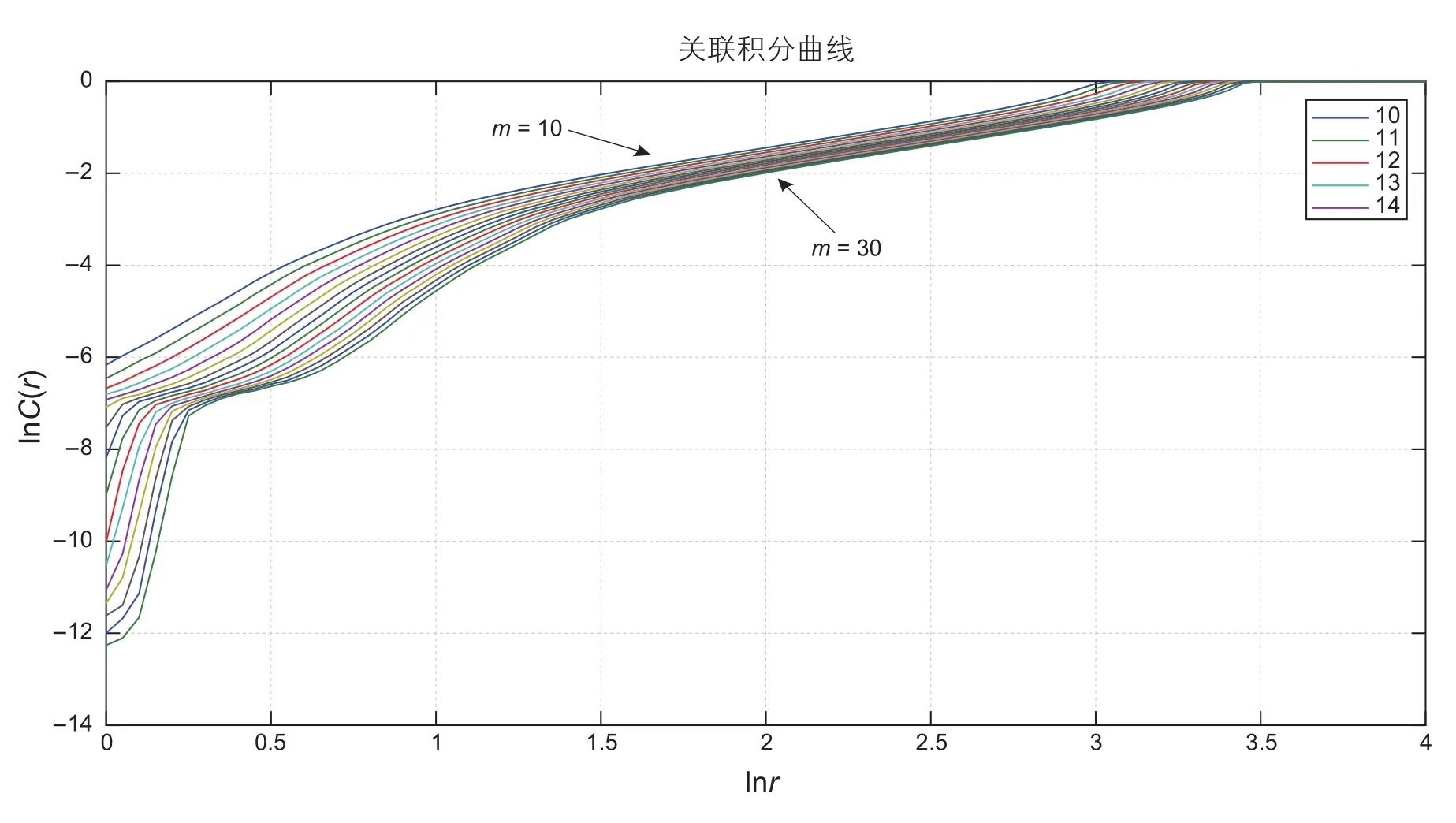
图4 信号的关联积分曲线Fig. 4 The correlation integral curve of signals

图5 信号的局部标度指数图Fig. 5 Local scaling exponent sketch of signals

由图中可以看出, 正常状态下(2010.7.29-2011.9.14，2012.2.23-2012.5.18)关联维数维数值在某一恒定数值(图中平均值为0.987 7)上下小范围波动(标准差为0.181 6)，2011年11月发生不平衡故障时关联维数值存在明显差异，增幅大约130％ (图中为2.277 3)，表明关联维数可以有效地对故障状态进行识别。降噪前后信号关联维数的对比如图9所示，更加直观的表明了降噪前后关联维数的差异性。

图6 2010-2012原始信号关联维数Fig. 6 The correlation dimension of raw signals between 2010 and 2012

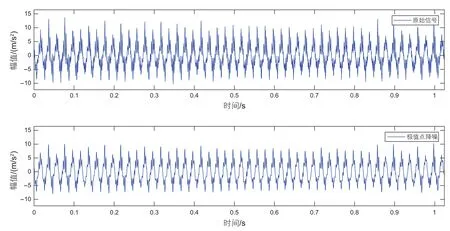
图7 原始信号与奇异值降噪后的时域波形Fig. 7 Time-domain waveforms of original and singular value de-noised signals

图8 2010-2012降噪后关联维数趋势Fig. 8 The correlation dimension of denoised signals between 2010 and 2012

图9 2010-2012各次降噪前后关联维数值Fig. 9 Correlation dimension of original and noise reduction between 2010 and 2012

最后，采用传统的自相关法[3]计算延迟时间并求得关联维数分布如图10所示。

图10 2010-2012基于自相关法的各次关联维数Fig. 10 Correlation dimension based on auto-correlation between 2010 and 2012

将对于复相关法，基于自相关法求得的关联维数各正常状态之间的波动情况较大(平均值为1.083 0，标准差为0.206 2)，故障状态的关联维数同正常状态相比仅增大58％(图中为1.715 4)，就故障分辨性而言，落后于复相关法。两种方法求得的关联维数的对比如图11所示。

图11 自相关法与复相关法计算所得关联维数值Fig. 11 Correlation dimension of complex and auto-correlation

4 结论

本文提出了一种极值点奇异值降噪与关联维数分布相结合的电机转子不平衡故障识别诊断方法，并应用到工程实际。该方法首先对电机振动信号进行极值点奇异值分解降噪，之后通过复自相关函数法确定延迟时间，Cao氏法确定嵌入维数，并采用G-P算法计算关联维数。计算结果表明，极值点奇异值分解降噪能够有效抑制信号中的噪声含量，使得信号中系统的确定性特征不被噪声淹没，保障正常状态与故障状态下振动信号的关联维数存在显著差异，能够用于故障的识别诊断。同传统的自相关法相比，本文所采用的复相关函数法，求得的正常信号关联维数之间的波动性更小，而同故障信号的关联维数之间差异性更大，表明基于复相关函数法的G-P算法求得的关联维数分辨性更佳，更适合于故障的识别诊断，

[1]付华, 尹丽娜.小波包分解在电机故障诊断中的应用[J].微电机, 2007, 40(5):86-89. [FU H, YIN L N. Application of wavelet packet decomposition in motor fault diagnosis[J]. Micromotors Servo Technique, 2007, 40(5):86-89.]

[2]绍辉, 赵庆贤, 李燕.关联维数在机械设备故障诊断中的应用研究[J].中国安全科学学报, 2006, 16(3):129-134. [SHAO H, ZHAO Q X, LI Y. Study and application of correlation dimension in fault diagnosis of machinery[J].China Safety Science Journal, 2006, 16(3):129-134.]

[3]王祝平.基于EMD、关联维数及神经网络的内燃机故障诊断系统的研究[D].武汉: 华中农业大学, 2007. [WANG Z P. Research on fault diagnosis system of internal combustion engine based on EMD, Correlation Dimension and ANN[D].Wuhan: Huazhong Agricultural University, 2007.]

[4]王浩, 张来斌, 王朝晖, 等.迭代奇异值分解降噪与关联维数在烟气轮机故障诊断中的应用[J].中国石油大学学报(自然科学版), 2009, 33(1):93-98. [WANG H, ZHANG L B, WANG C H, et al. Application of ISVD de-noising and correlation dimension in fault diagnosis of fue gas turbine[J].Journal of China University of Petroleum(Edition of Natural Science), 2009, 33(1):93-98.]

[5]李琳, 张永祥, 明延涛. EMD降噪的关联维数在齿轮故障诊断中的应用研究[J].振动与冲击, 2009, 28(4):145-148. [LI L, ZHANG Y X, MING Y T. Gear fault diagnosis based on correlation dimension pre-processed with EMD[J].Journal of Vibration and Shock, 2009, 28(4):145-148.]

[6]王美令, 陈果.基于关联维数和小波能量谱熵的碰摩故障智能诊断[J].振动与冲击, 2010, 29(8):174-178. [WANG M L, CHEN G. Intelligent diagnosis of rubbing based on correlation dimension and energy spectrum entropy[J]. Journal of Vibration and Shock, 2010, 29(8):174-178.]

[7]杨宇, 王欢欢, 喻镇涛, 等. 基于ITD改进算法和关联维数的转子故障诊断方法[J].振动与冲击, 2012, 31(23):67-70. [YANG Y, WANG H H, YU Z T, et al. A rober fault diagnosis method based on ITD improved algorithm and correlation dimension[J]. Journal of Vibration and Shock, 2012, 31(23):67-70.]

[8]张磊, 彭伟才, 原春晖.奇异值分解降噪的改进方法[J].中国舰船研究, 2012, 7(5):83-88. [ZHANG L, PENG W C, YUAN C H. An improved method for noise reduction based on singular value decomposition[J].Chinese Journal of Ship Reasearch, 2012, 7(5):83-88.]

[9]刘飞.基于关联维数和Kolmogorov熵的转子振动故障模式识别[D].沈阳: 沈阳航空工业学院, 2009. [LIU F. Vibration fault mode determination for rotor based on correlation dimension and Kolmogorov entropy[D].Shenyang: Shenyang Aerospace University, 2009.]

[10]KIA S H, HENAO H , CAPOLINO G A.Diagnosis of Broken-Bar Fault in induction machines using discrete wavelet transform without slip estimation[J]. IEEE Transactions on Industry Applications, 2009, 45(4).

[11]THEILER J.Spurious dimension form correlation algorithms applied to limited time-series data[J]. Physical Review A, 1986, 34 (3): 2427-2432.

Motor rotor imbalance fault recognition based on extreme point SVD de-noising and correlation dimension

YUAN Zhuang, DUAN Lixiang, WANG Jinjiang
College of Mechanical and Transportation Engineering, China University of Petroleum-Beijing, Beijing 102249, China

To improve the recognition of motor rotor imbalance faults, this paper presents a method based on the extreme point singular value decomposition (SVD) and the correlation dimension distribution. First, the motor vibration signals collected in different periods are de-noised using the extreme point singular value decomposition to avoid the misconvergence of correlationdimension caused by noise. Then the multiple correlation function replaces the traditional correlation function to determine the delay time, and a genetic programming (G-P) algorithm is utilized to calculate the correlation dimension. Finally, the motor rotor imbalance can be recognized by comparing the correlation dimension of multiple sets of vibration signals. We applied the developed method to a motor rotor imbalance in an oilfeld in western China, and the results demonstrate that the correlation dimensions of de-noised signals can effectively identify the motor rotor imbalance. Compared with the traditional method, the correlation dimensions obtained by the developed method are more differentiable and more suitable for motor fault identifcation.

motor; rotor imbalance; fault feature extraction; correlation dimension

2016-11-15

10.3969/j.issn.2096-1693.2016.03.038

(编辑 付娟娟)

袁壮, 段礼祥, 王金江. 基于极值点奇异值降噪与关联维数的电机转子不平衡故障识别. 石油科学通报, 2016, 03: 425-433

YUAN Zhuang, DUAN Lixiang, WANG Jinjiang. Motor rotor imbalance fault recognition based on extreme point SVD de-noising and correlation dimension. Petroleum Science Bulletin, 2016, 03: 425-433.doi:10.3969/j.issn.2096-1693.2016.03.038

*通信作者, jwang@cpu.edu.cn