基于局部搜索策略的混合算法同步综合换热网络

张春伟, 崔国民, 陈 上

(上海理工大学 新能源科学与工程研究所, 上海 200093)

基于局部搜索策略的混合算法同步综合换热网络

张春伟, 崔国民, 陈 上

(上海理工大学 新能源科学与工程研究所, 上海 200093)

针对复杂换热网络混合整数非线性问题，提出了一种由混沌蚁群算法、局部搜索策略和结构进化策略组成的混合算法，同步综合换热网络。首先采用混沌蚁群算法初步优化换热网络，蚂蚁个体根据混沌搜索机制遍历整个求解域。随后引入Powell法作为局部搜索策略，加强蚂蚁个体的局部搜索能力。最后结合结构进化策略，限制算法的搜索空间，优化蚂蚁个体表示的换热网络结构，并将优化后的信息反馈。蚂蚁会根据自身、邻居和反馈的信息作进一步搜索，直到算法收敛于全局最优解。通过算例对算法进行验证，结果表明，混沌搜索机制使混合算法具有很好的全局搜索能力；Powell法加强了算法的局部搜索能力，提高了求解精度；结构进化策略能够有效地缩减搜索区间，提高搜索效率。所以混合算法能够很好地兼顾处理连续变量和整型变量，适用于换热网络综合。

换热网络综合；混沌蚁群算法；局部搜索策略；Powell法

1 引 言

换热网络综合(Heat exchanger network synthesis, HENS)是过程系统工程的一个重要领域，其意义在于强化系统的能量回收能力，提高能量利用率和经济性。虽然国内外学者对此作了大量的研究工作，但换热网络实现全局最优化依然有很大困难。换热网络中存在表示换热器有无的0-1整型变量和表示换热器热负荷分布的连续变量，所以换热网络同步综合属于混合整数非线性规划范畴[1]。并且随着换热网络的日益复杂化，整型变量维数急剧增加，导致可行解个数呈几何级增长，而目前的整数优化技术还无法有效地处理规模庞大的混合整数非线性问题。

传统的确定方法如牛顿法、Powell法等，基于梯度或方向信息，能够得到局部区域的极小值，具有较高的计算精度，但对初始点的依赖性较大，易陷入局部最优解。随机性方法如差分进化、遗传算法等能够搜索整个求解域，具有较强的全局搜索能力，但优化结果易受种群多样性的影响。如果多样性较差，则算法易发生“早熟”收敛现象，此外，与确定性方法相比，其局部搜索能力也相对较弱。所以换热网络综合自身的复杂性和优化方法的局限性是阻碍换热网络实现全局最优化的两个关键因素。

混沌蚁群算法是一种基于混沌理论和自组织理论的新型群体智能算法，已成功地解决了电力资源分配[2]、参数辨识[3]等问题。混沌搜索可以不重复地遍历求解域中的每一个状态，具有很好的爬山和跳出局部最优的能力，所以比随机搜索更加有效[4～6]。但混沌蚁群算法依然存在一些不足，如在解决高维问题时计算复杂性高，局部搜索能力弱，得到的解精度较低等问题[7]。

鉴于此，本文以混沌蚁群算法为基础，提出了一种混合算法同步综合换热网络。引入Powell法作为局部搜索策略，加强算法的局部搜索能力和求解精度。提出结构进化策略优化蚂蚁个体表示的换热网络结构，促使其向最优结构进化，缩减搜索区间，增强算法的局部跳出能力，提高搜索效率。最后通过两个经典算例对算法进行了验证。

2 换热网络综合问题数学模型

2.1 超结构模型及其序列表示

图1 换热网络无分流的分级超结构Fig.1 Superstructure of heat exchanger network with no stream splits

2.2 目标函数

针对上述换热网络模型，以年综合费用值(包括投资费用与运行费用)为目标函数，其数学描述为：

3 采用局部搜索策略的混合算法

换热网络模型包含大量的等式和非等式约束，目标函数呈现严重的非凸、非线性，属于NP-hard问题[10]，即使小规模的换热网络也无法证实找到全局最优解[11]。所以为实现换热网络的全局优化，本文提出了一种同时优化连续变量和整型变量的混合算法，其基本框架如图2所示。混合算法中，蚂蚁个体在整个求解域内进行位置更新后，产生当前解，采用Powell法对其进行局部搜索，提高搜索精度。结构进化策略优化当前解对应的网络结构并控制算法的搜索空间。新的网络结构产生后，使用Powell法初步优化其热负荷，计算相应的目标函数值，并将其反馈给蚂蚁个体。若新解的目标函数值优于当前解，则将其更新。否则蚂蚁个体依据自身和邻居信息，继续进行搜索，直到找到全局最优解或满足算法结束条件。混合算法中的CAS算法、Powell法和结构进化策略的相关描述如下所示。

3.1 混沌蚁群算法

混沌蚁群算法中的搜索过程中包含两个连续阶段，即蚂蚁个体的混沌搜索阶段和整个种群的自组织阶段。单个蚂蚁的混沌行为到整个种群自组织行为的转变是通过引入一个连续改变的组织变量,nKy来实现的。为使蚂蚁个体在开始时进行混沌搜索，文献[7]引入Sole[12]给出的混沌函数并进行相应改进，得到如下变量更新公式(以种群pN中第n个蚂蚁，第K代更新为例)：

3.2 局部搜索策略-Powell法

Powell法一种求解无约束最优化问题的直接搜索法[13]，具有收敛速度快，求解精度高，无需计算导数等优点，较其他传统的局部优化方法更适合换热网络综合问题。Powell法搜索步骤如下所示：

Step 1确定变量维数N，即当前蚂蚁个体结构所包含的换热器个数，读取当前位置信息0Q。设置收敛精

其中N的最大取值为KN。

Step 3判断迭代计算是否结束：若满足下式，则得到解NQ，计算结束；否则转Step 4。

Step 4计算最速上升方向上函数()F Q的变化：

Step 5引进第(1)N+个搜索方向和新的点Qt：

Step 6方向替换判断：

① 若满足

则将QhN作为新的初始点，沿原方向搜索，即转Step 2。

② 若满足

则将QN作为新的初始点，沿原方向搜索，即转Step 2。

③ 若以上两条件均不满足，则转Step 7。

Step 7以QN作为起始点，沿方向DN+1进行一维搜索，并得到此方向上的极小值点QN+1。将方向Debig用

理想状态下，位置变量每一次更新后，都应使用Powell法进行局部搜索，但此方式会使计算时间成倍增加。所以本文通过在算法中构造局部搜索概率函数，实现局部搜索和全局搜索、搜索速度和优化质量之间的平衡，其具体形式如下所示：

式中K为迭代次数，c1、c2为比例系数，具体数值可根据具体算例确定。F1Δ和F2Δ为此蚂蚁个体上次和本次最优位置更新时所对应目标函数的差值，其中若本次计算无最优位置更新，则F2Δ取0。I为常数，确定使用Powell法局部搜索的步数。此局部搜索概率函数能够实现以下四个功能：

(1) Powell法对初始种群进行优化，使每个个体均有一个较优的初始位置。

(2) 每迭代I次，对所有个体使用Powell法进行一次局部搜索。

(3) 如果本次最优位置目标函数值下降较上次大，说明此处可能具有更好的解，则Powell法局部搜索的概率相应增大。

(4) 当算法计算到后期时，在组织变量的作用下，每只蚂蚁均已移动到整个种群最优解的附近，此时增大Powell法局部搜索的概率。

3.3 结构进化策略

图2 混合算法框架Fig.2 General structure of the presented algorithm

图3 四股流换热网络结构及其序列表示Fig.3 Superstructure and string of heat exchanger network with four streams

(2) 结构进化：此部分包含两个独立的子部分，即换热器生成操作和消去操作。由于种群中个体表示的换热网络结构存在差异，所以可通过构造进化概率函数来决定对当前结构采取何种操作，增加随机性。概率函数的具体形式如下所示：

图4 换热器生成操作Fig.4 Operation of generating heat exchangers

图5 换热器消去操作Fig.5 Operation of eliminating heat exchangers

(3) 结构判断：由于结构进化操作具有随机性，所以为提高进化效率，排除不合理结构，本文提出两条结构判断公式，即对流体上的换热器个数进行限制。执行进化操作后，分别计算冷、热流体上的换热器个数，当满足判断公式时，使用Powell法对初步优化新结构的热负荷分布；否则认为结构进化操作无效，重新执行。结构判断公式如下所示：

(4) 结构选择：新结构产生后，若其费用值较原结构低，则将其更新，否则以一定的概率接受新结构。选择概率函数形式如下所示：

3.4 混合算法计算步骤

图6 混合算法流程图Fig.6 Flow chart of the hybrid algorithm

4 算例分析

选取两个算例对混合算法进行验证。为了充分分析局部搜索策略与结构进化策略对混合算法性能的影响，首先采用结合局部搜索策略的CAS算法(未包含结构进化策略)对算例进行优化；随后采用结合局部搜索策略和结构进化策略的混沌蚁群算法(混合算法)对算例进行优化，并对计算结果进行分析。计算环境为WIN7系统下Fortran (Compaq Visual Fortran 6)编程，计算机参数为Intel(R) Xeon(R) CPU E5-2670 v2 2.5GHz 32GB RAM。

4.1 算例一

算例一选自文献[16]，由4股热流体和5股冷流体组成。算例的相关参数如表1所示。Zhu等[16]采用了模块分解以及一种非线性优化方法解决此算例，获得结果为2970483$·year-1。方大俊等[9]采用标准微分进化算法求解算例一，其获得的费用值为2944702$·year-1。Peng等[17]提出了一种基于模拟退火算法的双层优化方法，其获得最好结构的费用值为2935112$·year-1。

表1 算例一流股参数Table 1 Problem data of case 1

图7 局部搜索 CAS 算法优化结果(年综合费用:2932164$·year-1)Fig.7 Results of the CAS algorithm with local search strategy (total annual cost: 2932164$·year-1)

结合局部搜索策略的CAS算法对算例一的优化结果如图7所示，其年综合费用值为2932164$·year-1，图中括号内为流体温度值，下同。混合算法对此算例的最终优化结果如图8所示，此结构对应的年综合费用值为2927829$·year-1，较前者的费用值下降4335$·year-1。

表2为算例一的综合费用值与文献的对比结果，各个结果所对应的冷、热公用工程用量、换热总面积以及换热单元数等均已列出。由其可知，两优化结果均明显优于文献，表明获得了更优的换热网络设计。

图8 混合算法优化结果(年综合费用:2927829$·year-1)Fig.8 Results of the hybrid algorithm (total annual cost :2927829$·year-1)

表2 算例一与文献对比结果Table 2 Comparison of results from case 1 and literature

4.2 算例二

算例2取值文献[18]，包含6股热流体与4股冷流体，算例的相关参数如表3所示。Ahmad[18]采用夹点分析法获得了一个费用为707400$·year-1的网络结构。Ravagnani等[19]提出了一种由遗传算法和夹点分析法结合的混合算法优化算例一，其获得的网络结构费用值为5672821$·year-1。方大俊等[20]提出了一种基于罚因子协进化的微分进化算法以期提高算法的精度和效率，其获得的网络结构费用值为5615794$·year-1。He等[21]提出了一种基于均匀性准则的流体排列策略，并使用Powell法对给定的流体进行优化，其获得的最优结构费用值为5609271$·year-1。

图9 局部搜索CAS算法优化结果(年综合费用：5617319 $·year-1)Fig.9 Results of the CAS algorithm with local search strategy (total annual cost: 5617319 $·year-1)

结合局部搜索策略的CAS算法对算例二的优化结果如图9所示，其年综合费用值为5617319$·year-1。混合算法对此算例的最终优化结果如图10所示，此结构对应的年综合费用值为5607037$·year-1，较前者的费用值下降10282$·year-1。

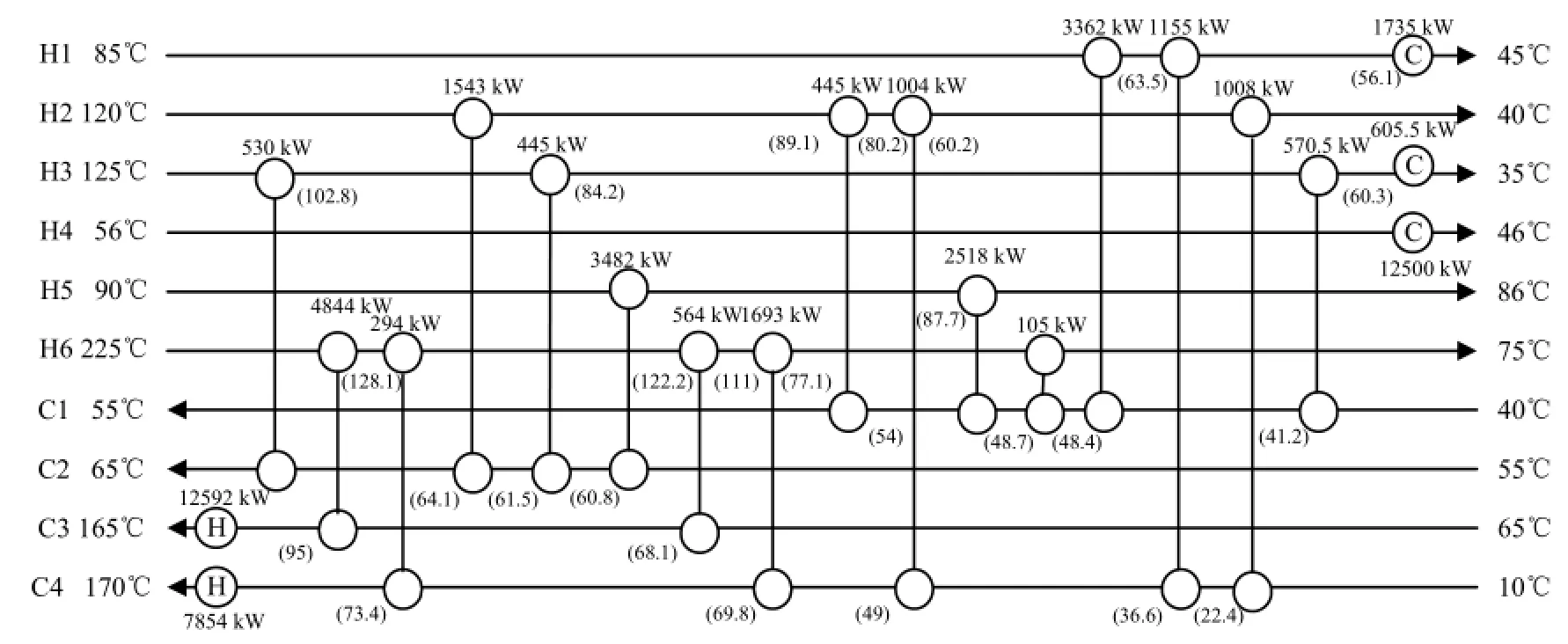
图10 混合算法优化结果(年综合费用：5607037 $·year-1)Fig.10 Results of the hybrid algorithm (total annual cost: 5607037 $·year-1)

表4为算例二的综合费用值与文献的对比结果，各个结果所对应的冷、热公用工程用量、换热总面积以及换热单元数等均已列出。由其可知，两优化结果均明显低于文献，表明了两优化结果所对应的换热网络结构相对更优。

表4 算例二与文献对比结果Table 4 Comparison of results from case 2 and literature

计算过程中的相关参数如表 5 所示，参数均为通过多次实验确定的经验值。由其可知，混合算法的计算时间相对较长，这是由于结构进化策略的随机性导致的。算例二两结果计算时间均长于算例一，因为算例二没有固定投资费用，其设定的换热器范围相应增大，变量维数较多，所以其计算时间有所增加。但通过分析两者的费用差值以及各自的换热网络结构可以发现，算例二的结构进化更加明显，即结构进化对于换热器个数较多的结构效率更高。

表5 计算相关参数Table 5 Parameters of the proposed algorithms

4.3 结果分析

为分析算法的性能，除每更新500步记录一个费用值外，同时记录迭代步数Kstart时的费用值，得到两者不同的年综合费用对比曲线。两算例的曲线图分别如图11、图12所示。

分析两图可知，结合局部搜索策略的混沌蚁群算法的费用曲线在前期下降速度较快，表明其局部搜索能力得到加强，但两算例均在计算Kstart步后，费用曲线几乎不再下降。因为此时个体的混沌行为减弱，种群已经收敛，其费用值优于文献结果，表明此算法具有一定的全局和局部搜索能力，但其在处理换热网络综合这类混合整数非线性问题时，存在一定的不足。

混合算法是在基于局部搜索策略的混沌蚁群算法计算Kstart步后，执行结构进化策略。观察其费用曲线可知，两算例的混合算法曲线均出现几次明显的下降过程。通过对比图7、8和9、10可知，两种算法所得结构的差异较大，表明结构进化策略使原结构得到了不同程度的进化，获得了更好的换热网络设计。

图11 算例一年综合费用对比曲线Fig.11 Comparison of total annual costs from the proposed algorithms for case 1

图12 算例二年综合费用对比曲线Fig.12 Comparison of total annual costs from the proposed algorithms for case 2

5 结 论

本文提出了一种基于局部搜索策略的混合算法同步综合换热网络，并通过两个经典算例对算法的性能进行了验证。结果表明，基于混沌搜索机制的CAS算法具有较强的全局搜索能力，与Powell法结合后，其局部搜索能力和求解精度得到增高。结构进化策略能够很好地处理换热网络综合中的整型变量，有效减少换热器匹配的数目规模，提高搜索效率，减少计算时间。反馈的优化信息又能进一步指引蚂蚁个体的搜索方向，对于换热器个数较多的算例，混合算法更容易取得较好的效果。所以本文提出的混合算法适合解决换热网络综合问题，具有很好的实用性。

符号说明：

[1] Ciric A R, Floudas C A. Heat exchanger network synthesis without decomposition [J]. Computers & Chemical Engineering， 1991, 15(6): 385-396.

[2] Cai J, Ma X, Li Q,et al. A multi-objective chaotic ant swarm optimization for environmental/economic dispatch [J]. International Journal of Electrical Power & Energy Systems， 2010, 32(5): 337-344.

[3] Peng H, Li L, Yang Y,et al. Parameter estimation of dynamical systems via a chaotic ant swarm [J]. Physical Review E， 2010, 81(1): 016207.

[4] Wang J, Tang Z, Wang R. An annealed chaotic maximum neural network for bipartite subgraph problem [J]. International Journal of Neural Systems， 2004, 14(02): 107-116.

[5] Ikeguchi T, Sato K, Hasegawa M,et al. Chaotic optimization for quadratic assignment problems [C]//Circuits and Systems, 2002. ISCAS 2002. Scottsdale: IEEE International Symposium on. IEEE, 2002, 3: III-469-III-472.

[6] Yuan Z Q, Huo Z J, Jiang C W. Economic dispatch and optimal power flow based on chaotic optimization [C]//Power System Technology, 2002. Proceedings. Kunming: PowerCon 2002. International Conference on. IEEE, 2002, 4: 2313-2317.

[7] LI Li-xiang (李丽香). An optimization method inspired by ‘chaotic’ ant behavior and its applications (一种新的基于蚂蚁混沌行为的群智能优化算法及其应用研究) [D]. Beijing (北京): Beijing University of Posts and Telecommunications (北京邮电大学), 2006.

[8] Yee T F, Grossmann I E. Simultaneous optimization models for heat integration—II. Heat exchanger network synthesis [J]. Computers & Chemical Engineering, 1990, 14(10): 1165-1184.

[9] FANG Da-jun (方大俊), CUI Guo-min (崔国民). Global optimization of heat exchanger networks using differential evolution algorithm (微分进化算法应用于换热网络全局最优化) [J]. CIESC Journal (化工学报), 2013, 64(9): 3285-3290.

[10] Furman K C, Sahinidis N V. Computational complexity of heat exchanger network synthesis [J]. Com puters & Che mical Engineering， 2001, 25(9): 1371-1390.

[11] Yerramsetty K M, Murty C V S. Synthesis of cost-optimal heat exchanger networks using differential evolution [J]. Computers & Chemical Engineering， 2008, 32(8): 1861-1876.

[12] Solé R V, Miramontes O, Goodwin B C. Oscillations and chaos in ant societies [J]. Journal of Theoretical Biology， 1993, 161(3): 343-357.

[13] Powell M J D. An efficient method for finding the minimum of a function of several variables without calculating derivatives [J]. The computer journal, 1964, 7(2): 155-162.

[14] Ravagnani M, Silva A P, Arroyo P A, et al. Heat exchanger network synthesis and optimization using genetic algorithm [J]. Applied Thermal Engineering， 2005, 25(7): 1003-1017.

[15] Dipama J, Teyssedou A, Sorin M. Synthesis of heat exchanger networks using genetic algorithms [J]. Applied Thermal Engineering，2008, 28(14): 1763-1773.

[16] Zhu X X, Oneill B K, Roach J R, et al. A method for automated heat-exchanger network synthesis using block decomposition and nonlinear optimization [J]. Chemical Engineering Research & Design, 1995, 73(8): 919-930.

[17] Peng F, Cui G. Efficient simultaneous synthesis for heat exchanger network with simulated annealing algorithm [J]. Applied Thermal Engineering, 2015, 78: 136-149.

[18] Ahmad S. Heat exchanger networks: cost tradeoffs in energy and capital [D]. Manchester: University of Manchester Institute of Science and Technology (UMIST), 1985.

[19] Ravagnani M, Silva A P, Arroyo P A, et al. Heat exchanger network synthesis and optimization using genetic algorithm [J]. Applied Thermal Engineering, 2005, 25(7): 1003-1017.

[20] FANG Da-jun (方大俊), CUI Guo-min (崔国民). Optimization of heat exchanger networks with cooperation differential evolution algorithm based on penalty factors (基于罚因子协进化微分算法优化换热网络) [J]. Journal of Chemical Engineering of Chinese Universities (高校化学工程学报), 2015, 29(2): 407-412.

[21] He Q, Cui G. A principle of stream arrangement based on uniformity factor for heat exchanger networks synthesis [J]. Applied Thermal Engineering， 2013, 61(2): 93-100.

A Hybrid Algorithm with Local Search Strategy for Simultaneous Synthesis of Heat Exchanger Network

ZHANG Chun-wei, CUI Guo-min, CHEN Shang
(Research Institute of New Energy Science and Technology, University of Shanghai for Science and Technology, Shanghai 200093, China)

Simultaneous synthesis of heat exchanger network is primarily regarded as complex mixed integer nonlinear programming models (MINLP). Therefore, a novel hybrid algorithm which consists of a combination of chaotic ant swarm algorithm (CAS), structure evolution strategy (SE) and local search strategy was proposed. Firstly, CAS algorithm (which ants can traverse the whole solution space based on chaotic search mechanism) was applied to obtain an initial network configuration. Subsequently, the Powell method was introduced as local search strategy to enhance the solution accuracy and stability. Finally, the structure evolution strategy built the structure represented by the ants and limited the search space. The evolved structures were sent to the CAS algorithm for guiding the next search of ants. Two cases published in the previous literature were examined to evaluate the performance of the presented algorithm. The results show that the obtained values are better than that reported previously. Thus the hybrid algorithm can simultaneously handle both continuous and discrete variables, and the local optimizing ability and the structural search ability are clearly enhanced.

heat exchanger network synthesis； chaotic ant swarm algorithm； local search strategy；Powell method

TK124

A

10.3969/j.issn.1003-9015.2016.00.035

1003-9015(2016)06-1380-11

http://www.cnki.net/kcms/detail/33.1141.TQ.20161117.1618.004.html

2016-01-12；

2016-05-12。网络出版时间：2016-11-17 16:18:36

国家自然科学基金(51176125)。

张春伟(1992- )，男，内蒙古通辽人，上海理工大学硕士生。

崔国民，E-mail：cgm1226@163.com