超声平面波两种数据压缩方法初步比较
张耀楠,金应东,,邱维宝
1 西安思源学院电子信息工程学院,西安市,710038
2 东北大学中荷生物医学与信息工程学院,沈阳市,110169
3 中国科学院深圳先进技术研究院生物医学与健康工程研究所,深圳市,518055
超声平面波两种数据压缩方法初步比较
【作 者】张耀楠1,2,金应东2,3,邱维宝3
1 西安思源学院电子信息工程学院,西安市,710038
2 东北大学中荷生物医学与信息工程学院,沈阳市,110169
3 中国科学院深圳先进技术研究院生物医学与健康工程研究所,深圳市,518055
超声平面波成像是超声成像研究的热点之一, 超声平面波带来超高帧频的同时也带来了超大数据量。如果将这些数据量直接通过硬件传输,势必对硬件带来极大的负担,也对硬件处理数据的能力提出了极高的要求。为了减少大数据量高帧频所带来的问题,该文通过数据压缩的方式来降低采集数据的传输量。分别从有损压缩和无损压缩方向进行了研究,选择了LZW压缩算法来尝试无损压缩的效果,而根据平面波特点,提出频域切割压缩算法作为有损压缩方法。将LZW算法在FGPA进行了实施,通过对超声仿真数据进行测试,可以达到一定的压缩比。在已知分数带宽的条件下,可以求出频谱中需要保留的带宽,而其余部分频率信号对图像影响的意义不大。通过对超声仿真数据的测试,频域切割压缩算法可以达到较高的压缩比,而比较原始图像和压缩重建图像,其差异是微小的。所以从压缩比角度,频域切割压缩算法是进行超声数据压缩的优先选择。
超声;平面波;数据压缩;LZW
0 引言
超声成像具有安全、方法简单、价格便宜、能够区分不同软组织等优点,使得超声成像在医院中得到广泛应用。传统的超声成像通常采用电子扫描的方式,进行多次聚焦发射来获得一幅完整的图像,所以成像帧频较低。近年来,超声平面波成像是研究的热点之一[1-3]。这种技术是通过向介质中发射一个宽度范围很大的波束,然后记录下反射的回波,最后运用数字平行接收波束合成[4]技术或者时间逆转聚焦技术[5-6]来最终形成需要的超声图像,很大程度上提高了成像的帧频。
平面波带来超高帧频优势的同时也带来了超大数据量。如果将这些数据量直接通过硬件传输,这势必对硬件带来极大的负担,也对硬件处理数据的能力提出了极高的要求。假设传输的数据一帧为4 000 ×128像素,而一帧的数据量就是4 000 ×128×2 byte。在超快成像领域一般采集速度可以达到上千帧,这里以1 000帧为例,则超声采集设备每秒钟理论需要传输的数据量为:4 000×128×2×1 000=1 GB,而当前USB3.0的数据传输速度最大能够达到的极限速率为300 MB/s,所以,对于海量的平面波数据来说,采集和传输的速率不成比例,这就给超声实时成像造成了极大的瓶颈。为了减少大数据量高帧频所带来的问题,本文通过数据压缩的方式来降低采集数据的传输量。目前国内外关于超声平面波数据压缩的研究还较少,本文描述超声平面波数据压缩的两种方法并加以比较。本文选择了LZW(Lempel Ziv Welch)压缩算法来尝试无损压缩的效果,而根据平面波特点首先提出频域切割压缩算法作为有损压缩方法。
1 LZW压缩算法及其硬件实现
1.1 LZW算法
LZW[7]算法有三个重要的对象,输入数据流,输出数据流和一张用于编码的字符串表。输入数据流指被压缩的数据;输出数据流指压缩后输出的代码流;字符串表存储的是数据的索引号,重复的数据流就是由同一索引号存储,从而实现了数据的压缩。
1.2 LZW算法硬件实现流程
LZW算法在FPGa[8]上具体的实现方式为:首先将FPGa初始化,设置两个大小为4 096的字符串表,他们轮流工作,即当其中一个字符串表满时就转到另一个字符串表工作,同时对刚才的字符串表进行清空操作,为下一次填表做准备。当FPGa准备就绪后,在第一个时钟脉冲上升沿到来时,向FIFo 1发出第一个读信号,则这个通道输送第一个待压缩的数据到FPGa的查字符串模块。经过数据比较单元比较之后,判断接收到的数据是否位于存储器中,如果在,则把这个数据左移八位放到寄存器作为数据前缀,同时向FIFo 1再发一个读信号,FIFo 1向FPGa输送下一个字节的数据,FPGa将移位寄存器中的前缀与这个字节的数据相加后形成新的字符串,再判断这个字符串是否位于字符串表中。如果不在字符串表中,则将这个新字符串添加到字符串表中,同时字符串表指针加一,然后将新的字符串表输出到FIFo 2存储器;如果在字符串表中,则将字符串表中的索引号作为前缀,继续接受下一个字节。如此循环,直至第一个字符串表满。当第一片字符串表满时,第一片的片选端置零,第二片选通,第二片字符串表开始工作。同时对第一片字符串表进行清空操作,为下一次工作做准备。当第二片字符串表满时,再选用第一片存储器,如此循环进行操作。当输入信号为空,即FIFo 1向FPGa发出空信号,表示数据传送完毕,压缩完成。
1.3 LZW算法用于超声平面波数据压缩实例
下面介绍LZW算法在超声平面波数据压缩中的应用,通过实际血管的仿真数据进行实验说明。假设从探头中得到的数据集位宽是16位的,也就是说数据数值分布在-1215~215-1。而LZW算法的一个要求是输入数据应该是大于1的整数,需要将原始数据转换成整数。
首先我们将数据分为4 096个数据块,比如(1~8),(9~16),······,然后将原始数据映射到每个数据块上。具体映射法如原始数据中某一位数值为2,可以发现它位于第一个数据块中,我们用4或者5也就是数据块的中间元素来替代它。对于原始数据的每一个元素都进行这样的操作,最终得到的新数据的冗余度将大大增加。最后使用LZW算法对数据进行压缩处理。处理结果如表1所示。

表1 LZW算法结果Tab.1 LZW compress result
LZW无损压缩算法的压缩比相较于频域切割压缩算法(将在后面介绍)并不理想,但是也能达到一定的压缩比。产生此差别主要有三方面的原因,第一方面是无损压缩本身压缩比没有有损压缩算法高;第二方面是由于超声波信号的特有性质决定了信号数据的冗余度并不高,使得LZW压缩算法没有发挥其特点,在GIF动态图压缩方面,LZW压缩算法就能将自己的优势发挥最大;第三方面是由于LZW算法除了输出压缩数据外,还需要传输解压缩的字典串表,这使得输出数据量增加了一倍,这也是压缩比不高的主要原因之一。
2 频域切割压缩算法
LZW算法是针对于信号的时域部分来进行压缩的一种算法。LZW算法不仅需要传输压缩后的数据,还需要将解压缩的字典串表一并发送给解压缩端,这增加了数据的传输量也就缩小了压缩比。而频域切割算法则是针对超声数据的频域特征来进行数据压缩的一种方法,而与LZW压缩算法不同的是,频域压缩算法属于有损压缩。
2.1 算法描述
在叙述算法之前,首先说明一个分数带宽的概念(Fractional Bandwidth, FBW)。分数带宽指标主要描述一个超声信号重要的主要频率所占总体频率的一个比例,其定义如下:

带宽BW通常指信号所占据的频带宽度,带宽有时候也称为频宽,以Hz为单位,而fc为中心频率。分数带宽更多是描述主频部分信号占据带宽的比例。如果分数带宽确定,中心频率越大,带宽也就越大。所以,当一个系统确定时,它的中心频率是确定的,可以通过公式求解出有效的带宽。在超声系统中,一般认为下降到-40 dB时的分数带宽就是主频信息基本保存完整的特征参数。所以在已知分数带宽的条件下,我们可以通过此公式求出频谱中需要保留的带宽,而其余部分频率信号对图像影响的意义不大。算法实质就是通过保留这段主要的频带信息通过后期数据的添加合成重建图像。每个超声探头都有其自己的特征参数,如图1示例。
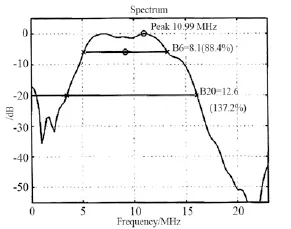
图1 探头的频域参数,中心频率fc=9.2 MHz,及在-6 dB和-20 dB处的值Fig.1 The spectrum parameter of an aperture with fc=9.2 MHz, and value at -6 dB and -20 dB
如图1所示,这个探头发射超声波的中心频率为9.2 MHz,在-6 dB和-20 dB处的FBW值分别为88.4%和137.2%。如果想保证超声成像不失真且主频信号完整,本文规定将参数控制在157%左右,也就是-40 dB处。结合公式(1),在知道探头中心频率的基础上,可以计算出可通过带宽,然后结合带宽计算出相应的起始点和结束点数。
频域切割算法的主要流程如下:
1) 将原始一个FIFo中的RF-data(Radio Frequency data)进行FFT傅里叶变换;
2) 由探头的中心频率和FBW计算出BW,由频谱图计算起始和结束点;
3) 在频域上将结束点以后的所有点都置为0,相当于截断无用频率信号点;
4) 将置零的个数存储,只将主频信号的数据和这个标记位上传;
5) 将主频数据进行IFFT傅里叶反变换,重建时域信号数据。
2.2 实验结果
针对上述算法,本文使用Field II(一种超声成像仿真软件)产生的囊肿仿真数据进行测试,将128振元的数据先提取一条扫描线的数据来进行试验,其他的数据压缩效果基本一致。Field II相关仿真参数为:fc=3.5 MHz, fs=50 MHz, elements numbers=128, kerf=0.05/1000。
由于超声图像每条扫描线中所包含的频率信息相似,所以,没有必要将所有的扫描线都进行算法分析,但是评判后期图像重建效果,每条扫描线进行算法实现是必要的,但是这并不影响压缩比的计算。通过对一条扫描线数据的FFT变化,经过对数压缩操作后得到了探头特征参数指标图,如图2所示。

图2 囊肿仿真超声数据频域参数Fig.2 The spectrum parameter of the aperture with cyst simulated ultrasound data
本文设置-40 dB时的FBW为主频通过的特征参数。下面通过图3来具体阐述所进行频域切割压缩算法的步骤。
图3中有四个单独的信号图,分别为a、b 、c 、d。图3a表示一条扫描线的原始时域采集信号,我们通过在128中随机选取一条扫描线的数据来进行试验测试,发现图像纵向深度大于5 000个点。然后对于图3a的时域信号进行FFT傅里叶变换,得到频谱图。在频谱图中,可以看出信号的频率以3.5 MHz为中心。然后通过计算BW的结束点差不多位于552个点,通过将其后的数据点置零得到压缩后的频域数据。
这里需要特别注意的一点是,图3b中显示的只是经过FFT后对称的一半信号,所以,置零的过程是将正负频率部分的点都换成0。也就是说,不仅仅是500~5 000个点置为0,5 000以后与前端信号对称的相应4 500个点都得置为0。这是由于FFT变换会产生信号的正负频率两部分,而这两部分的复数实部完全相同,但是虚部互为相反数。为了能够正确地将切断后的信号通过傅里叶反变换回去,就必须对应置零,否则信号将无法正确反变换。

图3 频域切割压缩过程Fig.3 The process of the frequency domain compression
图3c显示的就是由图3b频率信号经552点以后切断的频谱图。对称的另一半频率图缺省显示。图3d就是由图3c所截断置零以后的频域信号经过IFFT傅里叶反变换还原的时域信号。
以此类推,另外的128个通道的数据以同样的方式进行FFT变化,通过计算FBW和相应的带通点数,将结束点后的点进行舍弃操作,并将数据量用标志位进行记录。最后将压缩后的数据上传电脑后在电脑中实现数据的重建,最后成像。图4为原始图像与重建图像的对比。
从图4中,如果仅仅用人眼来区分,很难发现两幅图像存在的细微差别。这也正好说明了频域压缩算法的可行性。但是为了更具说服力,本文通过计算两幅图像的后期评价指标来进行量化比较。
图5显示了不同深度下的纵向分辨率。它们大多集中在246.4 μm,原始图像的分辨率稍好于重建以后的图像。图中小正方形的数值代表具体的分辨率大小。从五个不同深度的分辨率可以得出结论,频域切割压缩算法对于图像分辨率的影响微乎其微。

图4 原始图像与重建图像的对比Fig.4 comparison of the original image and the reconstructed image

图5 不同深度的纵向分辨率Fig.5 axial resolutions at different depths
表2显示了原始图像与重建图像在中间深度对比度与cNR (contrast to Noise Ratio)的值,从表2中可知,对比度比值为64:61,cNR则只相差0.04 dB。在这两项指标上,原始图像和压缩重建以后的图像差别十分微小。所以不管是从对比度,分辨率还是cNR上,我们可以得出结论:重建后的图像与原始图像相似度极高,频域切割压缩算法的可行性和正确性得到了验证。

表2 对比度与cNR在中间深度的比较Tab.2 The contrast and cNR in the mid-depth comparison of the two images
通过这样的压缩算法到底为我们节省了多少资源?压缩比的大小见表3。

表3 频域切割算法结果压缩结果Tab.3 one line data compression result
一条扫描线的总数据量为5 010个点,频域切割点从552个点开始。由于记录的点数是5 010个点,硬件上实现时只需要记录下来没有截取的数据和后续需要截取多少个0的标志位,而标志位在压缩比计算式忽略不计。所以压缩比的大小仅是数据总体长度5 010个点和截取剩下的552个点的比值,达到了9.076。而根据这个主频数据点和置零的标志位我们可以在Pc机上顺利地进行傅里叶反变换,重建出原始数据的5 010个点。对于128振元的通道依次处理将大大压缩平面波所带来的大数据量。
3 结束语
本文主要从时域和频域两个方面提出了两种对超声平面波大数据量进行压缩的方法,主要工作是在科学院深圳先进技术研究院生物医学与健康工程研究所完成的。两种方法各有它们的特点,主要针对当前硬件处理芯片无法及时传输大批量数据所提出。当使用频域切割压缩算法时,必须充分了解自己所要处理的超声信号特点,这样才能够给出正确的傅里叶变换和傅里叶反变换的方法。这种处理方式不管是在硬件还是软件上都是易于实现的。而LZW算法不需要将数据转换到频域进行计算,在硬件上实现操作也不是很难,但是LZW算法的压缩比由于需要字符串表的传输而大大减少。
从压缩比角度,频域切割压缩算法是进行超声数据压缩的算法优先选择。但要注意的是,频域切割压缩算法是一种有损压缩方法,虽然本文根据后期评价指标比较原始图像和压缩重建图像的差异来看,结果是微小的,但这种比较还是初步的。最终的比较还要根据最终的应用来判断频域切割压缩算法是否有影响。
[1] Tanter M, Fink M. Ultrafast imaging in biomedical ultrasound[J]. Ieee Trans Ultrason Ferroelectr Freq control, 2014, 61(1):102-119.
[2] couture o, Fink M, Tanter M. Ultrasound contrast plane wave imaging[J]. Ieee Trans Ultrason Ferroelectr Freq control, 2012, 59(12): 2676-2683.
[3] Garcia D, Le Tarnec L, Muth S,et al. Stolt's f-k migration for plane wave ultrasound imaging[J]. Ieee Trans Ultrason Ferroelectr Freq control, 2013, 60(9): 1853-1867.
[4] owen K, Fuller MI, Hossack Ja. application of x-y separable 2-D array beamforming for increased frame rate and energy effciency in handheld device[J]. Ieee Trans Ultrason Ferroelectr Freq control, 2012, 59(7): 1332-1343.
[5] asl BM, Mahloojifar a. eigenspace-based minimum variance beamforming applied to medical ultrasound imaging[J]. Ieee Trans Ultrason Ferroelectr Freq control, 2010, 57(11): 2381-2390.
[6] Gallot T, Perge c, Grenard V, et al. Ultrafast ultrasonic imaging coupled to rheometry: Principle and illustration[J]. Rev Sci Instrum, 2013, 84(4): 045107.
[7] 彭勇. 一种改进的LZW编码数据压缩算法的设计与仿真[J]. 信息与电脑, 2012, (2): 55-57.
[8] 刘荔. 全数字B超诊断仪中数字信号处理的FPGa设计与实现[D]. 杭州: 浙江大学, 2006.
Preliminary Comparison of Two Compression Methods for Ultrasonic Plane Wave Data
【 Writers 】ZHANG Yaonan1,2, JIN Yingdong2,3, QIU Weibao3
1 College of Electronics and Information Engineering, Xi’an Siyuan University, Xi’an, 710038
2 Sino-Dutch Biomedical and Information Engineering School, Northeastern University, Shenyang, 110169
3 Institute of Biomedical and Health Engineering, Shenzhen Institutes of Advanced Technology, Chinese Academy of Science, Shenzhen, 518055
Ultrasound, plane wave, data compression, LZW
R 445.1
A
10.3969/j.issn.1671-7104.2016.03.003
1671-7104(2016)03-0164-05
2016-01-29
辽宁省自然科学基金资助项目(201202071)
张耀楠,教授,e-mail: johanzyn@qq.com
【 Abstract 】Ultrasonic plane wave imaging is one of the hot topics in the study of ultrasound imaging, but the plane wave ultrahigh frequency ultrasound has brought a large amount of data. If these data are transmitted directly through the hardware, it will not only bring a great burden on the hardware, but also put a requirement for the ability of the hardware processing data. In order to reduce the problem caused by the high frame frequency and large amount of data, the data compression methods are used to reduce the amount of data acquisition and transmission. In this paper both lossy compression and lossless compression are studied, where LZW compression algorithm is chosen to test lossless compression effect, and based on the plane wave characteristics, the frequency domain cutting compression algorithm is developed as a lossy compression method. In this paper, the LZW algorithm is implemented in FGPA, and it can achieve a certain compression ratio after testing the ultrasonic simulation data. Under the condition of known fractional bandwidth, it is found that the main bandwidth can be preserved in the spectrum, while the rest of the frequency signal has little effect on the image. By testing the ultrasonic simulation data, the frequency domain cutting algorithm can achieve high compression ratio, and the difference between the original image and the reconstructed image is relatively small. So from the point of the compression ratio, the frequency domain cutting algorithm is the primary choice of the ultrasonic data compression algorithm.

