刷式密封泄漏流动特性流固耦合研究

刘宁宁，孙 丹，胡广阳，艾延廷，白伟钢

(1.沈阳航空航天大学 辽宁省航空推进系统先进测试技术重点实验室，沈阳 110136； 2.中国航发沈阳发动机研究所航空发动机动力传输航空科技重点实验室，沈阳 110015)

刷式密封泄漏流动特性流固耦合研究

刘宁宁1，孙 丹1，胡广阳2，艾延廷1，白伟钢1

(1.沈阳航空航天大学 辽宁省航空推进系统先进测试技术重点实验室，沈阳 110136； 2.中国航发沈阳发动机研究所航空发动机动力传输航空科技重点实验室，沈阳 110015)

刷式密封是旋转机械的关键部件，由其引起的泄漏损失直接影响旋转机械的工作效率。分析了刷式密封的流固耦合特性，应用双向流固耦合与动网格技术，建立刷式密封瞬态三维流固耦合求解模型。在实验验证流固耦合求解模型准确性的基础上，分析刷式密封的泄漏流动特性，研究刷式密封几何参数等因素对其泄漏特性的影响规律。研究结果表明，刷式密封泄漏量随着后挡板保护高度的增大而增加；随着刷丝束与后挡板之间轴向间隙的增大，泄漏量先增大，然后趋于稳定不变；随着刷丝排数的增加，泄漏量先迅速下降，然后下降速度趋缓。研究结果为刷式密封结构设计提供理论依据。

刷式密封；流固耦合；流场特性；泄漏特性

刷式密封是继篦齿密封之后发展起来的一种新型密封技术，能显著减小航空发动机二次流路气体泄漏[1]，被认为是已沿用多年的篦齿密封最简单、最实用和最有效的替代产品[2-3]。近年来，随着航空发动机增压比、推重比等性能的不断提高，航空发动机压力、转速等逐渐向高参数方向发展，由刷式密封引起的泄漏损失越来越大，直接影响航空发动机的工作效率[4-5]。

国内外学者基于计算流体力学理论对刷式密封泄漏流动特性做了大量的研究工作，国外Aksit[6]、Dogu[7]、Michael[8]等建立了定常稳态刷式密封non-darcian多孔介质模型，研究了不同密封径向间隙下的流场分布特性和泄漏特性。国内李军[9]、张艾萍[10]、黄学民[11]、江生科[12]等基于多孔介质模型，采用定常稳态数值求解方法，研究了刷式密封的泄漏流动形态以及后挡板轴向间隙、保护高度等参数对其影响规律。黄首清[13]建立了刷式密封三维切片模型，应用定常稳态数值方法研究了刷式密封流场分布特性以及刷丝排数对泄漏量的影响规律。研究表明，刷式密封刷丝在流体的作用下会产生变形，刷丝变形进一步影响流体分布，刷丝与流体之间的相互作用是典型的瞬态双向流固耦合问题[14-15]。现有文献关于刷式密封研究大多基于多孔介质模型，且采用定常稳态求解方法，对刷式密封泄漏流动特性的流固耦合研究较少。

本文在分析刷式密封流固耦合特性的基础上，应用双向流固耦合与动网格技术，建立了刷式密封瞬态三维流固耦合求解模型。在泄漏量数值计算结果与实验结果相互验证的基础上，研究了刷式密封的流场分布特性及刷式密封的设计参数(后挡板保护高度、刷丝束与后挡板之间轴向间隙、刷丝排数)对刷式密封泄漏特性的影响。

1 刷式密封流固耦合数值模型

1.1 刷式密封流固耦合模型

1.1.1 刷式密封流固耦合特性分析

刷式密封是具有优良密封性能的接触式动密封。传统刷式密封主要由前挡板、后挡板以及夹持在两部分间紧密排列的刷丝束组成，如图1所示。刷丝束是由柔软而纤细的刷丝交错层叠构成，沿着转子旋转方向呈30°～60°排列，保证了刷式密封能够适应转子的瞬间径向变形或偏心运动而保持良好的密封性能。研究表明，刷丝在气流力的作用下产生变形，刷丝变形进一步影响流场分布[16]，刷丝与流体之间的相互作用是典型的瞬态双向流固耦合问题。在气流力作用下，刷丝的轴向变形使密封与转子面间隙增大[17]，进而增加泄漏量，降低刷式密封封严性能。

图1 刷式密封结构实物图与示意图

1.1.2 刷式密封流固耦合模型理论分析

本文通过ANSYS Workbench数据交换平台提供的System Coupling模块实现刷丝和流场的双向耦合。刷丝变形分析采用ANSYS软件中的Transient Structural分析模块，流场特性采用CFX中RNGk-ε湍流模型进行分析，刷式密封双向流固耦合求解采用双重循环迭代方法[18]。耦合流程如图2所示，Tn时刻循环开始，以Tn-1时刻流场p、v的分布和刷丝变形的位移x结果信息作为初始条件，流体域经过若干子步计算收敛后，通过网格插值将得出流场p、v等分布信息传递到刷丝固体域耦合面，并以刷丝固体域耦合面为边界条件计算得到刷丝瞬态动力响应，然后将刷丝变形的位移x等信息再通过网格插值传递给流场耦合面。作为流场耦合面的边界条件，至此流体域与固体域的位移、载荷都达到收敛状态，则完成一次双向耦合迭代计算，继续进入Tn+1时刻循环。在双向流固耦合方法下，可获得任一时刻刷式密封流场压力速度分布特性和刷丝运动变形特性，并且该方法求解方式比较灵活，可以选择适合各物理场自身特点的计算方法进行求解，以达到较高的计算精度。

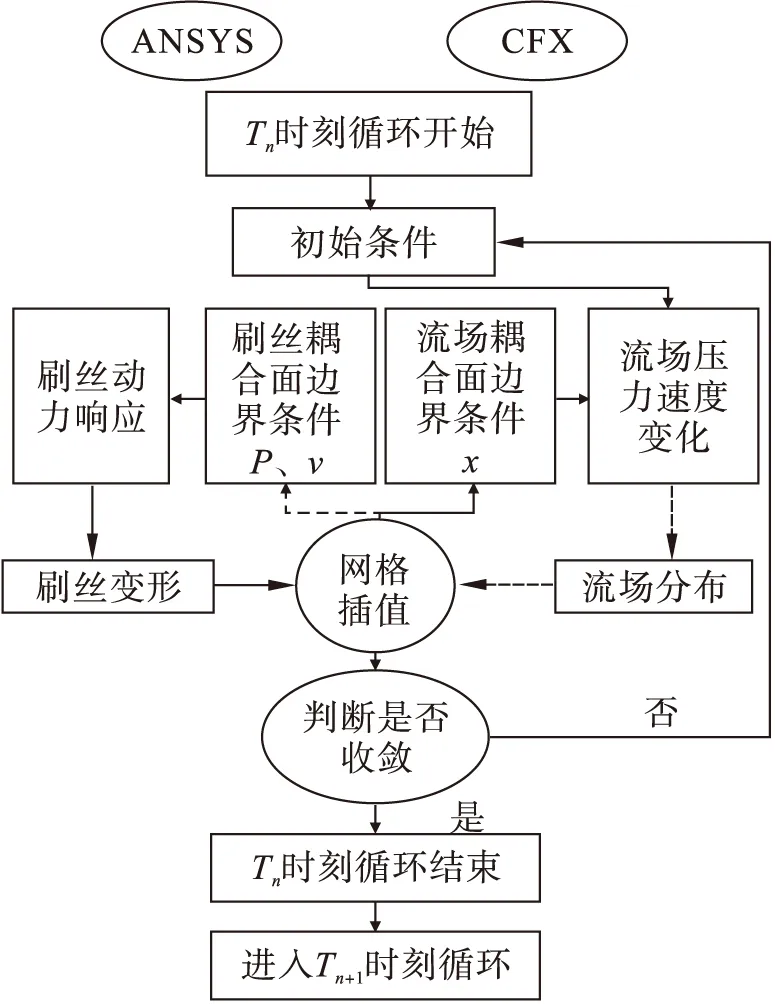
图2 流固耦合分析图

为提高数值结果的计算精度，将刷式密封流体域网格加密，这将引起耦合界面上流体域与固体域的网格不匹配，不能直接进行数据的交换，为此本文刷式密封流固耦合计算中采用守恒插值法。将气动载荷、网格变形等信息在刷丝与流体域间传递，即在耦合面上满足求解精度的情况下，保证能量传递守恒。若刷丝网格位移为Xs，通过传递函数[T]将刷丝网格位移转换为流场的网格位移Xf，表达式如下[19]

Xf=[T]Xs

(1)

在流体载荷的作用下，刷丝与流体域耦合面应满足能量传递守恒，即

(2)

则可以得出载荷在两个物理场之间传递关系

Fs=[T]TFf

(3)

式中Ff，Fs分别为作用在耦合面上的流体与刷丝载荷。

1.2 流体动力学模型

在文中双向流固耦合瞬态计算工况下，湍流流动守恒方程包括动量方程和连续方程

(4)

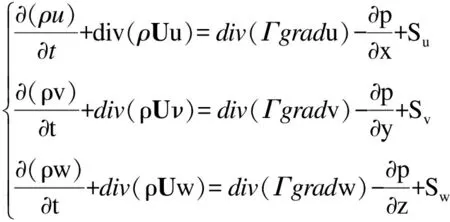
(5)

ρ为密度，t为时间，P为流体微元体上的压力，U为速度矢量，u、v和w是速度矢量U在x、y和z方向的分量，Г为扩散系数，Su、Sv和Sw为动量守恒方程的广义源项，即：

(6)

其中，Fx、Fy和Fz是流体微元体上的体力，若体力只有重力，且z轴竖直向上，则Fx=0、Fy=0、Fz=-ρg，μ为动力黏度，λ是第二黏度，一般可取λ=-2μ/3。

当刷丝受气动载荷作用弯曲变形时，刷丝束间隙流道高度弯曲变形，流场变得极其复杂。在弯曲流线的情况下，湍流是各项异性的，粘性系数μ是各向异性的张量。然而标准k-ε模型中对于Reynolds应力的各个分量，假定黏性系数μ是相同的，因此将标准k-ε模型用于包含有强旋流、弯曲壁面流动和弯曲流线流动的刷式密封流场时，会产生一定的失真，需要对标准k-ε模型进行修正，修正的RNGk-ε模型为：

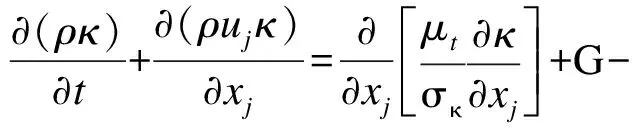
(7)

(8)

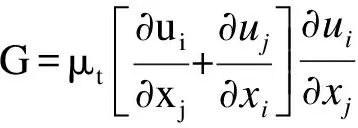
1.3 结构动力学模型

刷式密封刷丝在流体作用下的瞬态响应可通过求解结构动力学方程获得，有限自由度为n的结构动力学方程表示为

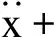
(9)

即

(10)

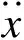
1.4 动网格技术分析

为准确模拟刷丝在流体作用下随时间的变形情况，本文采用动网格技术建立了刷式密封瞬态求解模型。当刷丝发生变形时，可将刷丝周围的网格的每个边看成一个弹簧，使用基于拉伸和扭转弹簧模拟的动网格方法，将刷丝变形信息传递给与它相邻的流体域耦合面每一个节点，进而将刷丝变形信息扩散到整个流体域。考虑到守恒性，每个节点上的合力必须为零，拉伸和扭转弹簧受力平衡方程分别为

(11)

(12)

式中Klij和(RijkTCijkRijk)分别为拉伸弹簧和扭转弹簧的平衡刚度矩阵，qij和qijk分别为拉伸弹簧与扭转弹簧的位移矢量。

2 刷式密封流固耦合求解模型

2.1 求解模型

本文以国内某型航空发动机内流系统高压压气机出口与卸荷腔之间的刷式密封为研究对象，采用流固耦合与动网格技术，建立了刷式密封流固耦合三维求解模型。为了简化计算，本文选取刷式密封前挡板以下区域内的刷丝束为研究对象，图3给出了刷丝排数为8排的刷式密封三维模型，包括固体域和流体域。图4为刷丝束间隙流场模型横截面示意图，其中刷丝长度为5mm，直径为0.15mm，刷丝间距为0.015mm，刷丝束与后挡板的轴向距离为0.5mm，后挡板高度为1.4mm，厚度为3.4mm，刷丝端部与转子面距离为0.1mm。刷丝材料为镍基高温合金，弹性模量为213.7GPa，泊松比为0.29。

图3 刷式密封计算区域

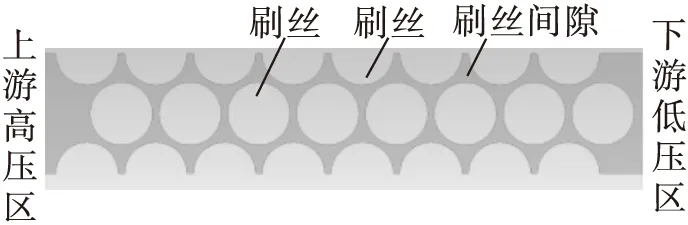
图4 刷丝束间隙流场模型横截面示意图

2.2 网格

由于刷丝间隙的细长比较大，为了满足计算精度，需要细化网格。图5为刷式密封计算网格示意图，本文采用混合网格形式，流体区域几何形状比较复杂，采用精细的四面体网格，使流体的流动迹线与网格分布的脉络相适应；刷丝区域几何形状简单，采用六面体结构化网格。本文进行了网格无关性验证，考虑计算精度与计算时间等因素，最终选定流体域网格数为40万，固体域网格数为10万。

2.3 边界条件

图6给出了刷式密封流固耦合建模的边界条件示意图。模型流体域进出口采用压力边界条件，入口总压为0.1 MPa，为了避免出口产生回流，右侧出口采用不设置流动方向的开放式出口边界条件，出口压力为0。双向流固耦合面边界如图6虚线框位置所示，包括两部分，由每排刷丝周向圆柱面和自由端圆面组成的固体域耦合面和与固体耦合面相邻的流体域面为流体耦合面，耦合面在瞬态多场求解器中设置为可移动边界条件。流场周向对称壁面采用不指定壁面边界条件，以便其能追随耦合面变形运动。转子面设置为指定变形边界，在笛卡尔坐标下，转子面在z轴正方向上按照正弦规律运动，表达式为A[mm]sin(w*t*1[s]-1)，A取0.1 mm,w=2π/t，t为流固耦合瞬态求解总时间，转子旋转表面线速度为300m/s。为了便于计算收敛，非定常求解计算以定常计算结果作为初始值。

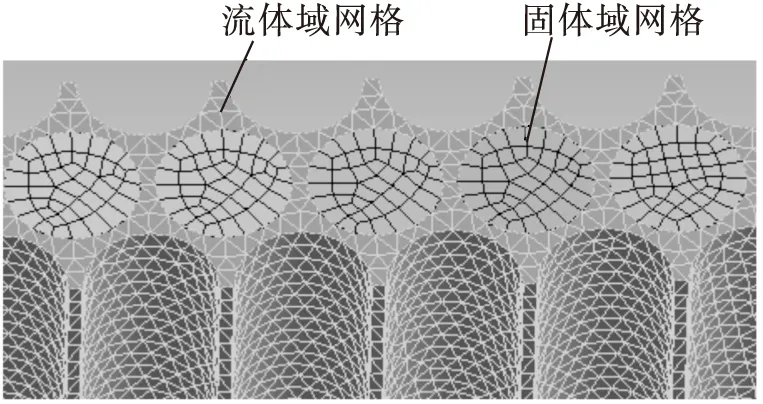
图5 刷式密封计算网格示意图

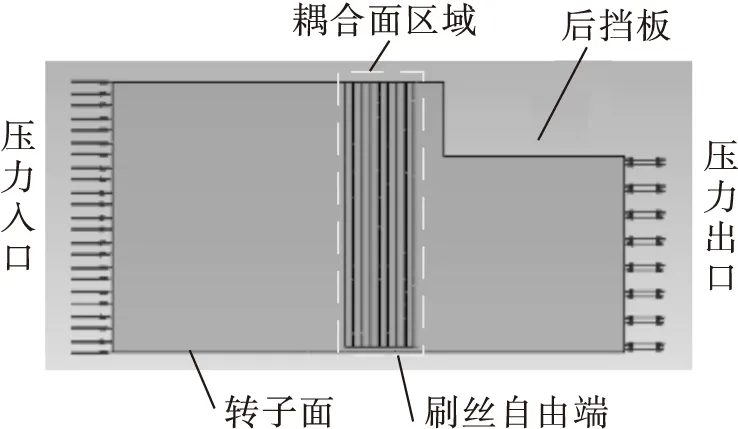
图6 刷式密封流固耦合模型边界条件示意图

3 流固耦合模型准确性验证

本文把实验得到的泄漏量与双向流固耦合计算结果进行对比分析，验证双向流固耦合数值方法的准确性。图7给出了以文献[20]的刷式密封结构为研究对象，采用本文双向流固耦合数值方法计算得到的泄漏量与文献[20]实验得到泄漏量的对比。由图7可以看出，在相同研究工况下，泄漏量的数值计算结果与实验结果的最大误差不超过6%，验证了本文双向流固耦合数值方法的准确性。

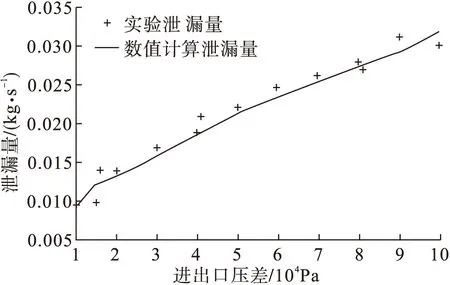
图7 本文数值结果与实验结果对比

4 结果与分析

4.1 流场分布特性数值结果与分析

4.1.1 压力分布特性分析

图8给出了刷丝排数为8排的刷式密封对称面与刷丝束横截面的压力分布图。由图8可以看出，上游入口区域压力基本保持不变，当流体进入刷丝束区域后，流体受到刷丝阻碍作用产生压降，压降主要集中在刷丝束间隙区域，压力沿着轴向逐渐降低。本文模型中刷丝束与后挡板有0.5 mm轴向间距，由图8中可以看出刷丝束与后挡板间隙区域处于同一较低压力值，刷丝束与后挡板间压力较小，有效降低了刷丝与后挡板间的摩擦力，可见刷丝束与后挡板的间隙可有效减弱滞后效应。

图8 压力分布图

4.1.2 速度分布特性分析

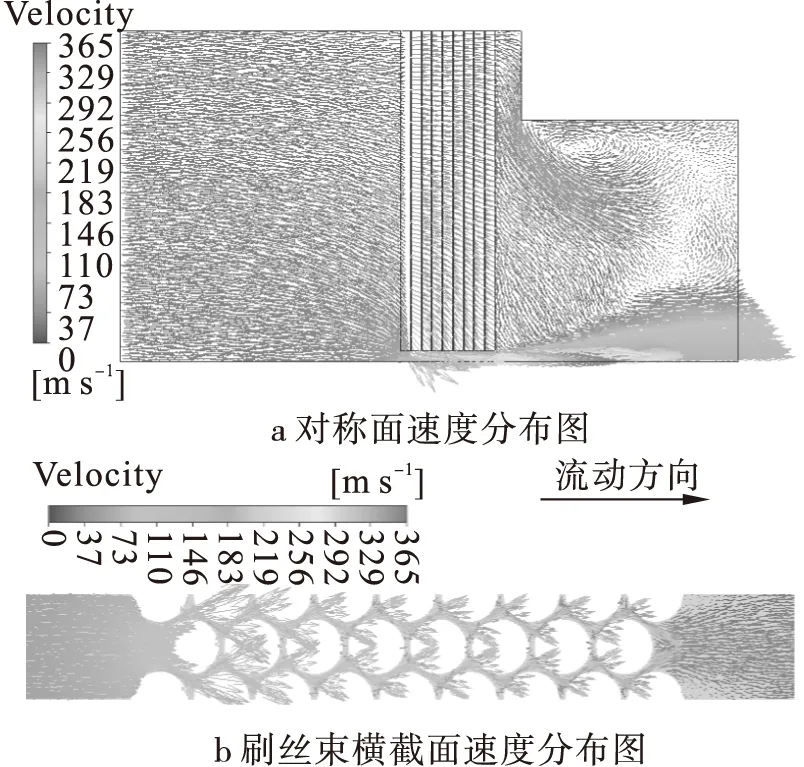
图9 速度分布图

图9给出了刷丝排数为8排的刷式密封对称面与刷丝束横截面速度分布图。由图9可以看出，流体以相同的初始速度进入刷式密封刷丝间隙以及刷丝与转子面间隙内，在压差的作用下流向后挡板和出口，当流经刷丝束后流体的轴向速度开始逐渐增大，而径向速度在后挡板附近急剧增大。刷丝束靠近上游和根部区域的流动非常微弱，最大速度发生在刷丝与转子面间隙处，流体成射流状射出。

4.2 泄漏特性分析

4.2.1 后挡板保护高度对泄漏量的影响分析

图10给出了不同进出口压比下，刷式密封后挡板与转子径向距离即后挡板保护高度对密封泄漏量的影响规律。由图10中可以看出，在不同进出口压比下泄漏量均随保护高度增大而逐渐增大。当压比较小时，泄漏量随着压比的增大而缓慢增加；当压比较大时，泄漏量随着压比的增大而显著增加。

4.2.2 后挡板轴向间隙对泄漏量的影响分析

刷丝束与后挡板之间的轴向间隙是影响刷式密封滞后效应的重要因素。图11中出了不同进出口压比下，刷式密封刷丝束与后挡板之间的轴向距离即轴向间隙对密封泄漏量的影响规律。由图11可以看出，在不同进出口压比下，轴向间隙从0.1 mm到0.3 mm，泄漏量均随轴向间隙增大而逐渐增大，并且当轴向间隙大于0.3 mm之后，轴向间隙继续增大对泄漏量的影响不大，即后挡板对刷式密封的密封作用贡献不大。

图10 后挡板保护高度对泄漏量的影响

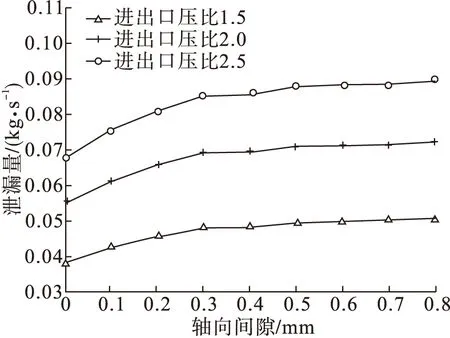
图11 轴向间隙对泄漏量的影响

4.2.3 刷丝排数对泄漏量的影响分析

图12给出了不同进出口压比下，刷式密封刷丝排数对密封泄漏量的影响规律。由图12中可以看出，刷式密封随着进出口压比的增大，泄漏量逐渐增大。在不同进出口压比下，刷丝排数从2排到10排，泄漏量迅速下降；刷丝排数从10排到18排，泄漏量下降速度趋缓；刷丝排数大于18排后，泄漏量基本稳定。由此可见，在本文研究工况下，刷丝束排数取为18即可达到一个相对较低的泄漏量，再增加刷丝排数对刷式密封的密封性能影响不大。

图12 刷丝排数对泄漏量的影响

5 结论

本文基于双向流固耦合与动网格技术，建立了刷式密封流固耦合三维求解模型，分析了刷式密封的流场特性以及几何参数等因素对刷式密封泄漏特性的影响规律，得出以下结论：

(1)刷丝束上游和根部区域压降和流动非常的微弱，刷丝束间隙中的流动从上游到下游不断加强，最下游成射流状。最大压降发生在刷丝束间隙区域，最大速度发生在刷丝束与转子面间隙区域；

(2)刷式密封泄漏量随着后挡板保护高度、刷丝间隙的增大而增加；随着刷丝束与后挡板之间轴向间隙的增大，泄漏量先增加，然后增大趋于稳定不变；

(3)随着刷丝排数的增加，刷式密封泄漏量先迅速下降，然后下降速度趋缓，最后趋于稳定。

[1]陈光.航空发动机结构设计分析[M].北京：北京航空航天大学出版社，2006.

[2]STEINETZ B M，HENDRICKS R C.Advanced seal technology in meeting next generation turbine engine goal[R].NASA/TM-1998-06961，1998.

[3]LELLI D，CHEW J W.Combined three-dimensional fluid dynamics and mechanical modeling of brush seals[J].Journal of Turbomachinery,2006,128(1)：188-195.

[4]邱波，李军.刷式密封流动与传热及力学特性的研究进展[J].热力透平，2013，42(3)：141-149.

[5]孙晓萍.刷式密封设计与试验研究[J].航空发动机，2005，31(2)：17-19.

[6]AKSIT M F.Effects of geometry on brush seal pressure and flow fields:Part II backing plate configurations[J].Journal of Turbomachinery,2006,128(4)：379-389.

[7]YAHYA DOGU.Evaluation of flow behavior for clearance brush seals[J].Journal of Engineering for Gas Turbines and power,2008，131(1)：82-93.

[8]MICHAEL FLOUROS.Thermal and flow phenomena associated with the behavior of brush seals in aero engine bearing chambers[J].Journal of Engineering for Gas Turbines and power,2015,137(9)：092503.1-092503.12.

[9]李军.基于多孔介质模型的刷式密封泄漏流动特性研究[J].西安交通大学学报，2007，41(7)：768-771.

[10]张艾萍.低滞后刷式密封泄漏流动数值模拟及结构优化[J].润滑与密封，2015，40(5)：67-42.

[11]黄学民.刷式密封中泄漏流动的多孔介质数值模型[J].航空动力学报，2000，15(1)：55-58.

[12]江生科.后夹板结构对刷式密封泄漏特性和温度分布的影响[J].动力工程学报，2015，35(9)：715-721.

[13]SHOUQING HUANG.Theoretical and experimental investigation on tip forces and temperature distributions of the brush seal coupled aerodynamic force[J].Journal of Engineering for Gas Turbines & Power,2014，136(5)：775-791.

[14]白花蕾，吉洪湖，曹广州.指尖密封泄漏特性的实验研究[J].航空动力学报，2009，24(3)：532-535.

[15]邢景棠，周盛，崔尔杰.流固耦合力学概述[J].力学进展，1997，27(1)：19-38.

[16]宗兆科.动压式指尖密封工作状态及其影响的流固耦合分析[J].航空动力学报，2010，25(9)：2156-2162.

[17]E.TOLGA DURAN.Brush seal structural analysis and correlation with tests for turbine conditions[J].Journal of Engineering for Gas Turbines and Power，2016，138(1)：201-213.

[18]吕坤.不同来流下薄平板流固耦合特性分析[J].中国电机工程学报，2011，31(26)：77-82.

[19]张磊.电站动叶可调式轴流风机叶轮动力特性研究[J].中国电机工程学报，2014，34(24)：4118-4128.

[20]MIKE T TURNER.Experimental investigation and mathematical modelling of clearance brush seal[C]//GT 2011-51197.ASME Turbo Expo 2008：Power for Land，Seal and Air.Berlin，Germany，GT2008-51197.

(责任编辑：吴萍 英文审校：赵欢)

Study on the leakage flow characteristics of brush seals based on fluid-structure interaction

LIU Ning-ning1，SUN Dan1，HU Guang-yang2，AI Yan-ting1，BAI Wei-gang1

(1.Liaoning Key Lab of Advanced Test Technology for Aerospace Propulsion System，Shenyang Aerospace University, Shenyang 110136,China; 2.Key Lab Power Transmission Technology for Aero-Engine，AECC Shenyang Engine Research Institute,Shenyang 110015,China)

Brush seals are the key parts of rotating machines,because leakage loss caused by brush seals affect the work efficiency of the machine.In this paper,the leakage flow characteristics of brush seals were analyzed using the theory of fluid-structure interaction.A three-dimensional computational model was presented based on two-way fluid-structure interaction,and moving grids technique and its validation was tested by experiment.The flow field characteristics were further analyzed and the effects of some factors(e.g.geometric parameters)on the leakage characteristics were also investigated.Numerical results show that the leakage rate increases with the increase of backing plate fence height.The leakage rate increases with increasing the axial clearance between the brush bristle and back plate,and then tends to be stable.As the bristle row number increases,the leakage rate first decreases rapidly,then slowly,and finally tends to a value.The results of this study can provide fundamental support for designing brush seals.

brush seals;fluid-structure interaction;flow field characteristic;leakage characteristic

2016-04-25

国家自然科学基金(项目编号：11302133)；航空基金(项目编号：2014ZB54)；辽宁省自然科学基金项目(项目编号：2015020113)

刘宁宁(1989-)，男，河南许昌人，硕士研究生，主要研究方向：旋转机械密封流体特性，E-mail：LNN_5568@163.com;孙丹(1981-)，男，辽宁丹东人，副教授，博士，主要研究方向：旋转机械密封流体特性，E-mail：phd_sundan@163.com。

2095-1248(2016)06-0035-07

TK263

A

10.3969/j.issn.2095-1248.2016.06.006