基于CATIA的飞机部件自动制孔路径规划
刘艳梅,王 鑫,马跃晏
(沈阳航空航天大学 自动化学院,沈阳 110136)
基于CATIA的飞机部件自动制孔路径规划
刘艳梅,王 鑫,马跃晏
(沈阳航空航天大学 自动化学院,沈阳 110136)
在飞机装配过程中,为了提高制孔的效率、制孔的定位精度和加工的质量,提出了一种自动制孔路径规划方法。通过CATIA软件建立飞机部件模型,采取改进的粒子群算法进行路径规划,从而获得一条最优路径进行自动制孔。仿真结果表明,改进的粒子群算法不仅很明显地提高了全局范围内的搜索能力,还充分改善了制孔方式的无目的性问题。
CATIA;自动制孔;粒子群算法;路径规划
飞机装配中,结构件连接主要是机械连接,还有一部分是铆接和螺栓的连接。根据统计,结构连接部位导致了70%的飞机机体疲劳失效事故,而连接孔处导致了80%的疲劳裂纹。随着科技技术不断进步,自动制孔在各方面性能都得到了很大的提高。它纠正了传统手工制孔在效率、质量、物力成本等问题上存在的缺点,并且可以满足飞机制造业中对制孔效率以及定位精确度的要求,从而提高了飞机的高疲劳寿命。20世纪90年代以后,我国在飞机装配技术、柔性装配技术上得到了巨大的发展[1],并引进了一些自动制孔设备,但由于技术问题没有形成生产力。而在国外,虽然自动制孔的科技和设备结构十分复杂,但是通过不断研制与应用也已达到了一定高度的水平。在国际上,飞机部件的自动制孔系统已经十分成熟[2]。在我国,航空制造领域中的研究与应用还十分落后,尤其是在应用软件的研究和模拟仿真方面还没有达到一定的水平。对于自动制孔技术来说,最重要的就是制孔前对路径规划算法的研究。目前,国内研究者提出了很多算法[3],如蚁群算法、遗传算法、神经网络算法和粒子群算法等解决路径规划的问题。1995年粒子群算法由Kennedy和Eberhart[4]等一起提出的,是一种进化计算技术,研究灵感来源于对鸟群捕食行为[5]。该算法在很多领域上引起了很多学者们的关注和广泛的应用,如神经网络训练、函数的优化问题和路径规划等[6]。20世纪90年代至今,国内外很多学者对粒子群算法进行了大量的研究及应用,取得了理想成果。
根据飞机部件装配的需要,利用飞机三维数字化模型,提取所需要的制孔点信息,通过粒子群算法对制孔路径进行最优规划[8]。文中提出了一种动态调整粒子群算法中惯性因子的策略,该算法的收敛速度和搜索全局最优能力极大增强,并通过不断地迭代,找到一条最优路径来实现自动制孔技术。通过仿真实验表明,改进的粒子群算法可以规划出一条最优路径来实现自动制孔。
1 自动制孔路径规划原理

建立表1ParSwarm和表2OptSwarm,路径访问表1ParSwarm将已经访问的粒子的位置、速度与当前粒子的适应度值记录在表中,即是当前粒子的最佳位置。全局最优解以及历史最优解,即最优路径的选择由表2OptSwarm记录。通过不断的迭代来寻找到一条最优路径实现制孔。假设有N个粒子,每个粒子维数为D,位置用W表示,速度用V表示,当前粒子的适应度值用F表示,全局最优解用Wg表示,每个粒子的历史最优解用(Wj,1)表示。粒子群初始阶段表1ParSwarm的前N行与表2OptSwarm中的相同,而Wg的值为表2OptSwarm中适应度值的最大值对应的行。
2 改进粒子群算法的自动制孔路径规划
2.1 粒子群算法
粒子群算法的基本思想是随机初始化粒子群,在给定的解空间中每个粒子都有初始位置和速度,并且都有一个解,而且每一个解都是一条路径。通过不断的迭代,从很多的解中找到一个最优解,也就是想要得到的最优路径。

表1 粒子当前位置、速度及适应度值
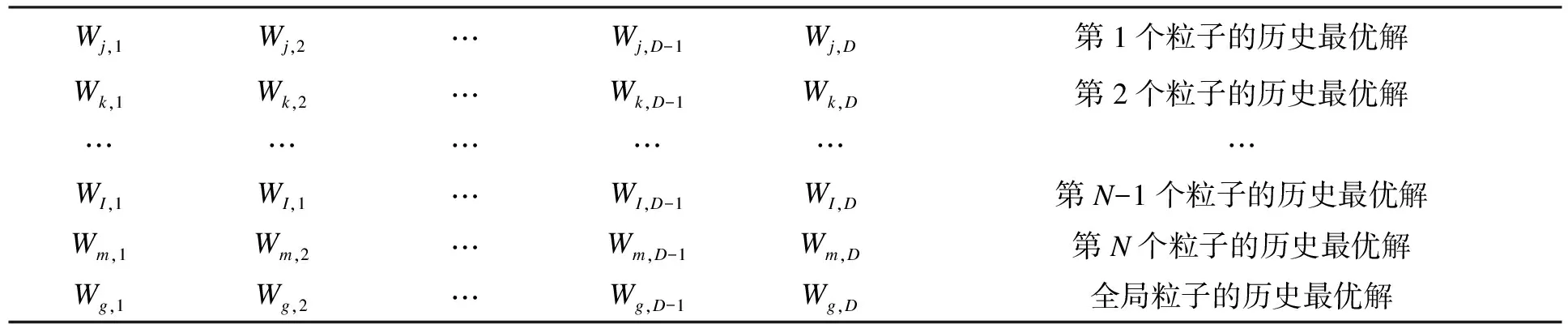
表2 粒子历史最优解
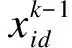
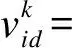
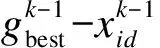
(1)
(2)
式中:c1和c2是加速常数;rand1和rand2是随机函数;pbest是粒子i的历史最佳位置;gbest是群体内的历史最佳位置;ω是惯性权重。
2.2 改进粒子群算法的自动制孔路径规划
典型的路径规划是指在具有障碍物的工作环境下按一定评价标准寻找一条从起始状态到目标状态的无碰撞路径。路径规划的优劣直接影响制孔的定位精确和效率程度,所以制孔要选择一种优秀的路径规划算法。目前已有许多优化算法解决该问题,但某些算法存在一定的局限性。
在自动制孔过程中,我们把制孔设备的路线模拟为鸟群觅食飞行过的路线,即要在一群鸟随机搜索食物的路线中寻找到一条最短路线[11]。改进的粒子群算法提高了该算法的性能。改进的粒子群算法在刚开始的时候每个粒子都不断地增加全局搜索范围,让它们在搜索速度上变快,其目的是在最短时间内确定最优解的一个大致位置。为了改善该算法的性能,同时可以在之后的局部搜索空间中通过逐渐降低搜索速度提高精确度,惯性权重的取值决定该算法的收敛速度。采用改进后的粒子群算法,即调节非线性惯性权重参数的研究来提高该算法的收敛速度,也增强了粒子种群群体的全局搜索能力,使其不易陷入局部最优解,最终找到全局最优解,并真正实现最优路径。
在搜索过程中不断更新该算法中粒子的位置和速度,导致算法容易出现缺陷。不断迭代会导致速度趋向于线性递增,直到最后都无法到达很好的局部搜索,无法满足路径规划的要求[12]。该算法前期受粒子个体历史最佳适应度(pbest)和群体历史最佳适应度(gbest)等诸多影响而使粒子找不到一条最优路径。经过大量的研究发现,可以有效控制粒子的飞行速度,使全局搜索和局部搜索之间的能力能够平衡,该算法还不能只根据假设一定的最大速度vmax满足要求。因此,针对上述问题,需要对粒子群算法进行改进。
改进粒子群算法的路径规划具体实现过程如下:
(1)首先在初始范围内,对种群中的每个粒子速度及维数进行随机初始化;
(2)每个粒子都要根据适应值函数式计算出适应值,即路径长度;
适应度函数在粒子群优化算法中非常重要。每个粒子的优化函数都代表的是粒子的路径长度。若粒子想获得最优解,必须通过更新个体历史最佳位置和更新全局最优位置,而适应度函数决定最优位置。通过比较粒子当前位置和历史最佳位置的适应值,若当前位置的适应值为优,说明粒子的当前位置为个体历史最优位置,进行更新个体历史最佳位置;同理更新全局最优位置;最后粒子获得的最优解即为最优路径。将粒子的历史最优解记录在表2OptSwarm中,表示鸟飞过离食物最近的一条路径。本文中选择路径长度作为适应值函数,如式(3)所示。
f(x)=
(3)
式中:f(x)表示粒子路径长度;(xi,yi,zi)表示粒子中每个顶点的坐标。
(3)通过比较粒子当前位置和历史最佳位置的适应值,若当前位置的适应值优说明粒子的当前位置为个体历史最优位置,进行更新个体历史最佳位置;
(4)比较每个粒子历史最佳位置和群体内的历史最佳位置的适应值,若历史适应值为优,说明全局最优位置是由当前粒子的历史最优来完成更新;
(5)根据式(1)和式(2)对粒子位置和速度进行更新,并根据公式(4)对惯性权重参数进行调整;
随着不断的研究发现可以调整速度公式中的参数惯性权重。当ω达到最大值时,该算法的全局搜索能力在大幅提高,而此时也降低了局部搜索能力;当ω到达最小值时,该算法加强了局部搜索能力,而减弱了新区域的探索能力。为了使该算法的全局搜索和局部搜索能力平衡,构造一种比较合适的惯性权重策略,研究者陆续地提出许多种改进惯性权重的策略。例如线性递减权重是为了解决粒子群算法在全局搜索最优解时出现振荡现象的一种算法。所以本文采用非线性变化的权重,让惯性权重ω从最大值减小到最小值,增加算法的局部搜索能力[13],非线性惯性权重的函数形式通常如式(4)所示。
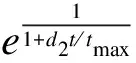
(4)
其中,d1,d2为控制因子,目的是控制ω在ωmax和ωmin之间。通过大量实验表明,随着不断地迭代,惯性权重ω非线性从0.9减少到0.4。所以当d1=0.2,d2=7,ωmax=0.9,ωmin=0.4时,增强了该算法的性能。
(6)通过不断地迭代寻找一个最优解形成最优路径。如果未达到终止条件,则返回(2)。
3 仿真结果及分析
本文将改进粒子群算法进行路径规划,并应用在飞机部件自动制孔中[14]。在CATIA中导入已经建立的数模,获得全部的制孔类型,并拾取全部自动制孔的孔位点位置,如图1所示。
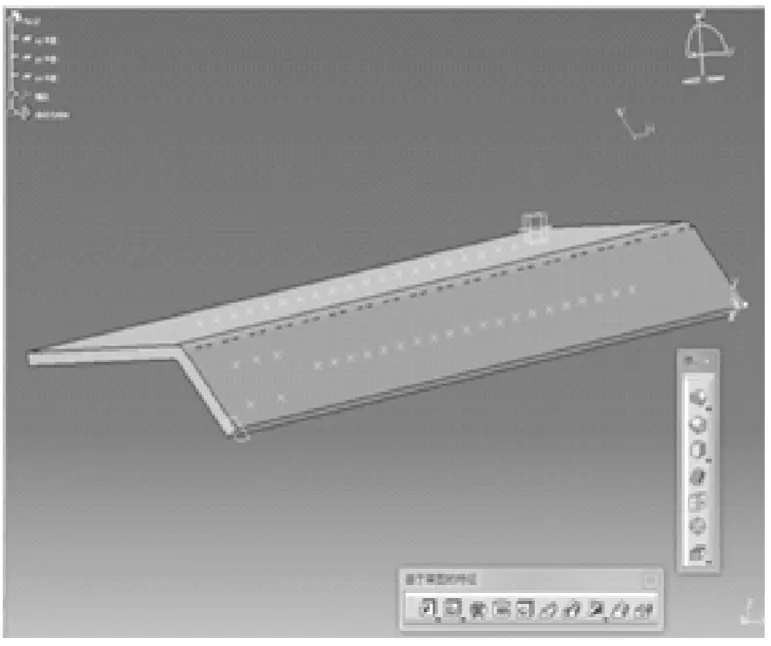
图1 拾取自动制孔点
在整个搜索过程中,根据非线性递减的思想决定惯性权重的取值,该算法中有很多重要的参数。实验结果表示,取45个孔位置,粒子个数为30,循环次数为500,加速因子c1取2,约束因子c2取1,可得到部件局部自动制孔的最优路径规划,如图2所示。
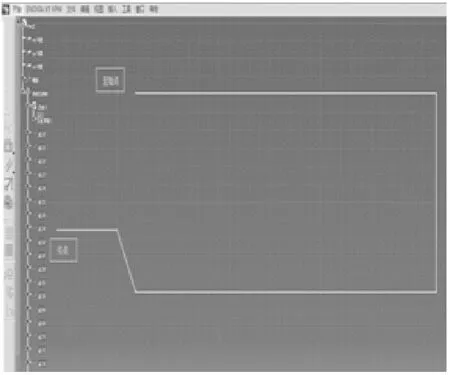
图2 飞机部件最短自动制孔路径
对上述算法中进行测试,为了使该算法的全局搜索和局部搜索能力平衡。本文改进粒子群算法在最优解、路径长度上都有所改善。为了更加直接地展现改进粒子群算法在搜索过程中具有一定的方向性,通过仿真得到改进粒子群算法和基本粒子群算法的收敛性曲线对比图,如图3所示。
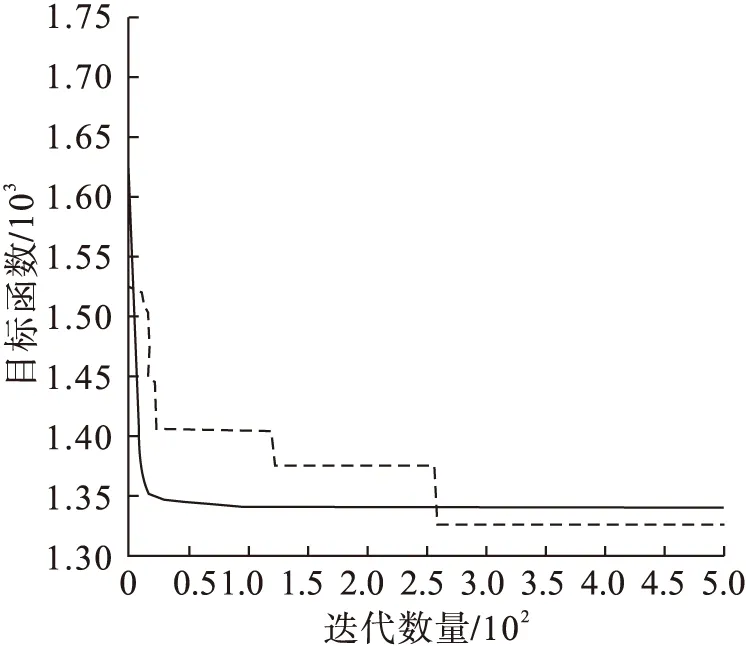
图3 收敛曲线对比图
图3中虚线表示传统粒子群算法的收敛图,实线表示改进粒子群算法的收敛图。传统粒子群算法的最短路径是1372.7250,而改进粒子群算法的最短路径是1334.1720。改进粒子群算法比基本粒子群算法更精确、更稳定。由图3可见,改进粒子群算法能更快地收敛到最小值。改进的粒子群算法进行路径规划,使收敛速度的更快、时间使用更少和路径长度更短,主要解决全局搜索能力和收敛速度慢的问题。
4 结论
本文针对飞机部件[15]自动制孔对路径规划问题,提出一种改进粒子群算法,即在搜索过程中改变惯性权重策略,降低该算法的随机性选择,并增强制孔路径的实时性,从而获得一条最优路径。从时间和空间来看,提高了收敛性和搜索能力等特性,结果表明改进的粒子群算法克服了传统粒子群算法的缺点,为自动制孔路径规划提供了指导。由实验仿真结果可知,对设计出的部件而言,本文提出的改进粒子群算法获得了一条最短路径来实现自动制孔,并取得了较好的效果。
[1]王嵛,刘浩,田威,等.面向飞机自动化装配的机器人工作姿态规划[J].中国制造业信息化,2012,41(13):50-54.
[2]刘长毅.飞机自动化装配中的机器人制孔动力学研究[J].航空制造技术,2012,17(16):26-29.
[3]吴小文,李擎.果蝇算法和5种群智能算法的寻优性能研究[J].火力与指挥控制,2013,38(4):17-20.
[4]KENNEDY J,EBERHART RC.Particle swarm optimization[C].Proceedings of IEEE International Conference on Neural Networks,Piscataway,New Jersey,1995,1942-1948.
[5]彭喜元,彭宇,戴毓丰,等.群智能理论及应用[J].电子学报,2003,31(s1):1982-1988.
[6]汤可宗,杨静宇.群智能优化方法及应用[M].北京:北京科学出版社,2015:71-102.
[7]胡挺,吴立军.CATIA二次开发技术基础[M].北京:电子工业出版社,2010:47-74.
[8]齐从谦,王士兰.CATIA V5R21三维数字化建模与动态仿真基础教程[M].北京:清华大学出版社,2012:27-75.
[9]韩志仁,郭文杰.基于MBD飞机装配自动制孔路径规划研究[J].机械设计与制造,2015,4(10):201-203.
[10]SHI Y H,EBERHART RC.A modified particle swarm optimizer[C].IEEE International Conference on Evolutionary Computation,Anchorage:IEEE,1998.
[11]张万绪,张向兰,李莹.基于改进粒子群算法的智能机器人路径规划[J].计算机应用,2014,34(2):510-513.
[12]潘峰,李位星,高琪.粒子群优化算法与多目标优化[M].北京:北京理工大学出版社,2013:15-19.
[13]张龙,王华奎.粒子群优化算法中惯性权重的研究[J].机械管理开发,2008,23(6):6-7.
[14]刘军.机器人自动制孔技术在飞机装配中的应用[J].航空制造技术,2014,5(17):104-107.
[15]韩志仁,刘晓波,胡烨.基于CATIA/CAA的快速标注方法研究[J].沈阳航空航天大学学报,2012,4(29):17-21.
(责任编辑:刘划 英文审校:齐义文)
Automatic path planning of hole making for aircraft components based on CATIA
LIU Yan-mei,WANG Xin,MA Yue-yan
(College of Automation,Shenyang Aerospace University,Shenyang 110136,China)
In order to improve the efficiency of hole making,positioning accuracy and the quality of machining,an automatic path planning method of hole making was proposed in aircraft assembly.Specifically,the 3D model of aircraft components was built by using CATIA software first.Then an improved particle swarm optimization algorithm was adopted to achieve the path planning,and consequently an optimal path was obtained.Simulation results show that the new particle swarm optimization algorithm not only significantly improves the global search capability,but also fully improves the aimlessness of the hole-making method.
CATIA;automatic hole making;particle swarm optimization;path planning
2016-10-28
航空科学基金(项目编号:2015ZE54026)
刘艳梅(1974-),女,吉林松原人,副教授,主要研究方向:系统建模与控制,E-mail:lymcml@126.com。
2095-1248(2016)06-0066-05
TP23
A
10.3969/j.issn.2095-1248.2016.06.011

